本記事の内容
本記事は、初等整数論を学習するに当たり、「そもそも初等整数論はどういう歴史をたどってどういうモチベーションで発展してきたのか？」という、ある種学習のモチベ上げをする記事です。
本記事を読むに当たり、特に何か予備知識が必要というわけではありませんが、高校数学は履修しているとより読みやすいかと思います。
本ブログでは、初等整数論以外にも記事がございますので、ぜひ他の記事も御覧ください！
数の発見
ここではサラッと述べるだけにします。
歴史上最初に発見された”数”は自然数です。
自然数が生まれたとき、人類は農耕や畜産を主としていたようですが、そのときに「今年は小麦がどれくらい取れるかな？」やら「今日は何頭のイノシシが取れたかな？」という発想で、足し算(加算)が生まれたようです。
そこから「何人で何頭のイノシシを取ったのか？」という発想で掛け算(乗算)が生まれたようです。
その後、インドで「\(0\)」という数が発見されました。
余談
\(0\)はインドで発見されたと言われています。インドで\(0\)が生まれたきっかけとして仏教がある、という説があります。
仏教の般若心経に「色即是空空即是色」という一節があります。
これは「なにもない」という状況があると仏教では捉えているという見方ができるそうです。
そういう理由で仏教が栄えたインドで\(0\)が発見されたのではないか？という説があるようです。
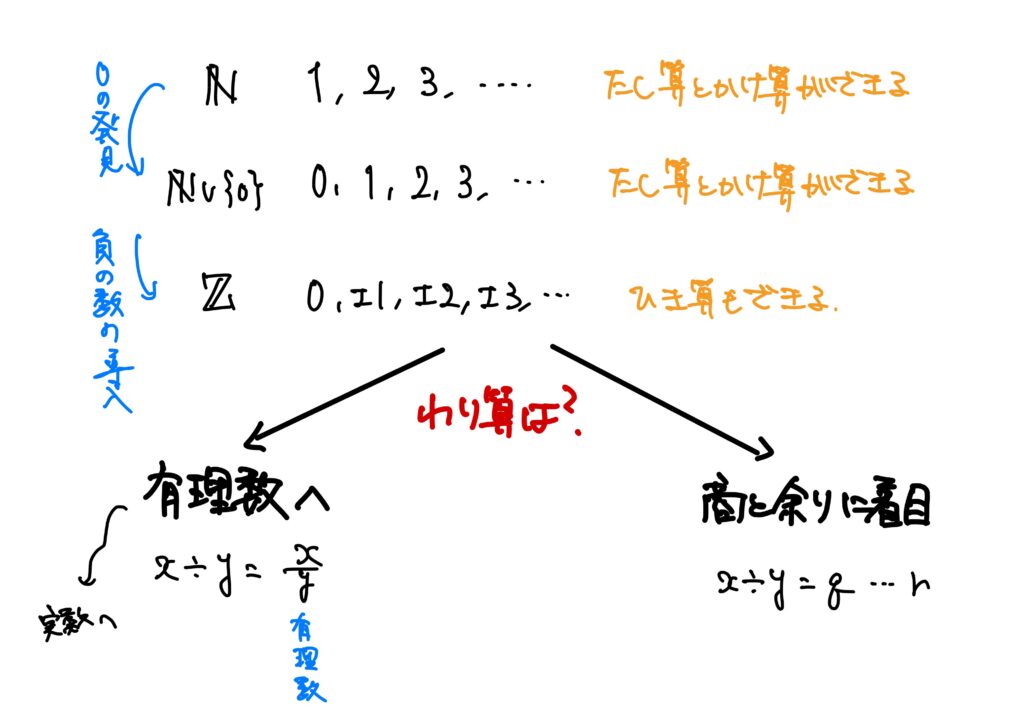
\(0\)が導入された自然数(現代の記号でいうと\(\mathbb{N}\cup\left\{0\right\}\)※後述)でも加算と乗算ができます。
その後「負の数」というものが導入され、それまで「足し算」と「掛け算」しかできなかったのが「引き算」もできるようになりました。
我々が知っている演算は他に「割り算(除算)」があります。
割り算を考えるときに、立場が２方向に別れました。
それが
- 有理数の発見(有理数への拡張)
$$
x\div y=\frac{x}{y}
$$ - 商と余りに着目する
$$
x\div y=q\cdots r
$$
(※\(\cdots\)は”あまり”の意)
という立場です。
初等整数論は2つ目の「商と余りに着目する」という立場を取った分野です。
実数については連続性から解説していますので、そちらを御覧ください。(実数の連続性)
例えばどんな問題が初等整数論の問題なのか？
例を3つほど挙げます。
\(x^2+y^2=z^2\)を満たす正の整数を求めよ。
\(x,y,z\)が仮に実数であれば、\(x^2+y^2=z^2\)を満たす\((x,y,z)\)は半径が\(z\)の円周上の点ですが、整数に限定すると円周上のどんな点でしょうか？
\(x^n+y^n=z^n\ (n\geq3)\)を満たす自然数\((x,y,z)\)は存在しない。
(※これは「フェルマーの最終定理」というより「フェルマーとワイルズ、その他多くの偉大な数学者たちの定理」と呼ぶべきなのかもしれません)
\(51458246518^{6561881751324}\)が\(3\)の倍数であるかをどう判定するか？
このように、実数まで広げず、整数に限定するだけでも意外と面白く、かつ難しい問題が生まれます。
(初等)整数論は整数のいろいろな性質(偶奇性やら互いに素やら)に着目したり、他の様々な数学の分野と結びつけたりして発展します。
ちなみに、巨大な整数の扱い方は現代では暗号通信に応用されています(1970年代〜)。
RSA暗号については後でちょっとだけ語ります。
筆者が思う整数論の面白さ
筆者は専門として数論、特に整数論を学んだわけではありませんが、個人的な整数論の面白さをちょっとだけ語りたいと思います。
主張自体はシンプルなのに、いざ真偽を確かめようとすると難しい
先程紹介したフェルマー(とワイルズ、その他多くの偉大な数学者たち)の(最終)定理が良い例だと思います。
御存知の通り、フェルマーの最終定理はフェルマーの死から実に330年経ってからようやく解決されました。
それほど真偽の判定が難しい主張というわけですが、もう一度フェルマーの最終定理の主張を見てみると
フェルマーの最終定理
\(x^n+y^n=z^n\ (n\geq3)\)を満たす自然数\((x,y,z)\)は存在しない。です。
正直なところ、主張の真偽はともかくとして、主張の内容は中学生でも分かる程度のものだと思います。
しかしながら、実際に解いてみようとすると、数多の偉大な数学者たちがこぞって挑戦したとしても300年以上もかかるという難解さです。
何がいいたいか、というと「主張自体はシンプルなのに、いざ真偽を確かめようとすると誠に難しい」ということが面白さだと思う、という話です。
例えば、問題文自体が非常に難解であれば、「これは難しい問題なんだなあ」と直感的に分かると思います(もちろん、蓋を開けてみるとそうでない場合もありますが)。
しかし、整数論は問題文がシンプルで「なんだ、この問題は簡単そうだな」という印象を受けたとしても、実は真偽の判定が誠に難しいというある種の印象とは相反する性格を持っていると感じています。
ここが面白さだと思うわけです。
発想力が問われる
さらに、整数論の面白さとして「発想力が問われる」という部分もあると思います。
例えば、先程あげた
\(51458246518^{6561881751324}\)が\(3\)の倍数であるかをどう判定するか？
という問題は、\(51458246518^{6561881751324}\)をせっせと計算し、さらに\(3\)で割れるかな？と筆算をすれば確かに求まります。
しかしながら、これは膨大な時間と労力がかかってしまいます。
そこで合同式なるものを導入して、合同式の普遍的な性質から\(51458246518^{6561881751324}\)が\(3\)の倍数か否かを判定するという方法で解くのが一般的です。
このように、たしかに力技でも解けるような問題でも、ちょっとだけ考え方を変えるだけで劇的に解きやすくなるというのもまた整数論の面白さだと思います。
先の例で言えば、合同式を導入することは整数を3つのグループ(\(3\)で割り切れる整数のグループ、\(3\)で割って\(1\)余る整数のグループ、\(3\)で割って\(2\)余る整数のグループ)に分ける、という発想です。
この発想によって膨大な時間と労力を削減しつつ、解答もシンプルになります。
初等整数論の応用例(RSA暗号)をちょっとだけ
“暗号”というと「秘密の文章を分かる人にだけ伝える」というようなニュアンスがあると思います。
数学における暗号もおおよそ同じような意味です。
暗号の起源は意外と古く、その歴史は古代ローマ時代にまで遡ります。
もちろん当時は国家機密を扱ったりと、ごく一部の人たちに対するだけのものでした。
情報社会の現在、暗号は我々の日常には欠かせないものとなっています。
少々ネタバラシすると、例えばTwitterやLINEやらのSNSを使うとき、自身のアカウントにログインしますが、平たくいえば、その時点でも実は数学が使われています。
(読み飛ばしてOK)
「数学って何の役に立つの？四則演算ができればそれでいいんじゃないの？」という質問を投げかける方がいます。もちろん、それは大事な発想だと思います。
しかし、数学を少しかじった方ならおわかりだと思いますが、数学は至るところで活躍しています。
個人的に、先のような質問が出現するのは「数学はあまりにも世の中に役立ち過ぎているがゆえに、身近すぎるがゆえに、案外恩恵がわからないものなのかな」と思っています。
要するに「灯台下暗し」というやつです。
暗号のイメージ
まずはイメージから。
次のような法則を考えます。
送られてきた文章のアルファベットに対して、\(a\)を\(b\)に、\(b\)を\(c\)に、\(\cdots\)、\(y\)は\(z\)に、\(z\)は\(a\)に変換する。
要するに、アルファベットを一つずらすという法則です。
この法則を書いた紙と「\(gdkkn\)」と書かれた紙を読者のあなたに手渡ししました。
つまり、この法則とメッセージは筆者と読者のあなたのみが知っているということです。。
他の方が見れば「gdkkn？なんだそれ？」となるところを、あなたは先の法則を使って「ああ、\(hello\)ね」と分かるわけです。
この場合、メッセージを読み取るための「鍵」が法則が書かれた紙ということになります。
(※この方法は共通鍵暗号方式といいます。)
通常の暗号は、先の例のように同じ「鍵」を使って暗号化と復号化(元の文章に戻すこと)を行い、情報の送り手と受け手の間で安全な方法(極端に言えば手渡し)で事前に鍵を共有しておきます。
しかしながら、ネット通販などで顧客がネットショップ側に個人情報やクレジットカード番号やらを送るには、事前に鍵を安全な方法で共有することができません。
公開鍵暗号とその仕組み
先の問題を解決するために開発された方法が「公開鍵暗号」です。
この方法は、暗号化する「公開鍵」と復号する「秘密鍵」の２種類の鍵を用意して、暗号化のための公開鍵のみを知っていたとしても、暗号化された情報を復号できないようにしています。
では、どのように情報を送受信しているのか、ということを見てみましょう。
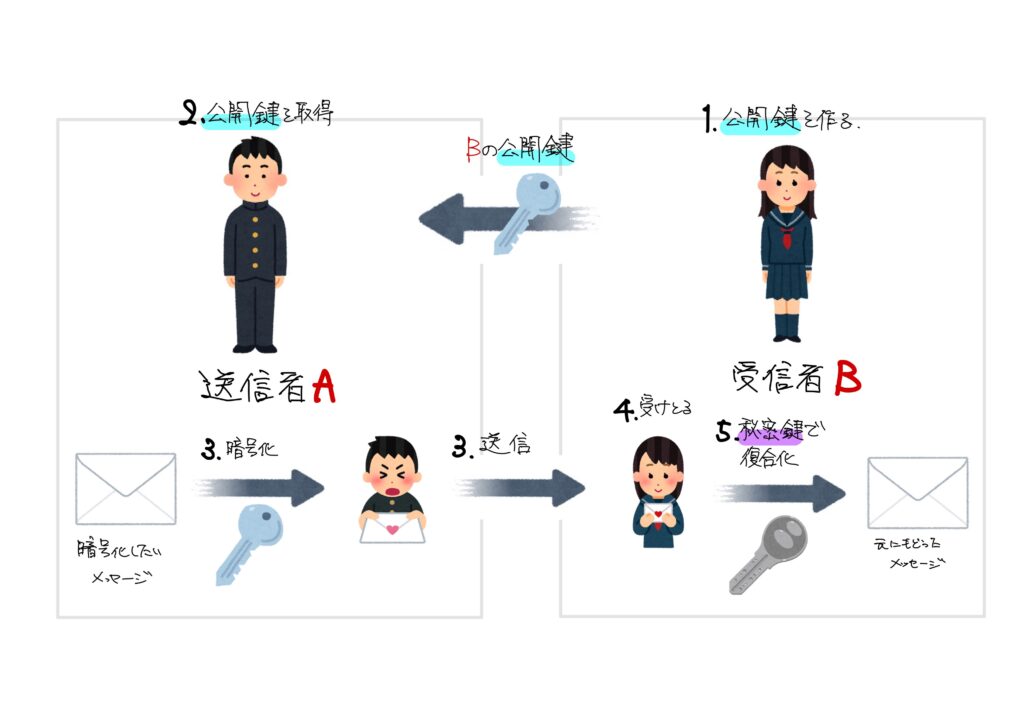
用意するものは「公開鍵」と「秘密鍵」の2つの鍵です。
公開鍵は誰でもかんたんに入手できるような、文字通り公開された鍵ですが、秘密鍵は1しかない大事な大事な鍵です。
流れはシンプルです。
- 受信者が公開鍵を作る。
- 送信者は受信者の公開鍵を取得する。
- 暗号化したいメッセージを送信者が公開鍵を使って暗号化し、送信する。
- 受信者が暗号化されたメッセージを受け取る。
- 受信者は暗号文を秘密鍵で暗号化する前のメッセージに復号化する。
このように、受信者(秘密鍵を持っている人)のみが暗号を解くことができるという仕組みになっています。
秘密鍵は受信者が大切に保管して、公開鍵は誰でも手に入れら場所に公開されています。
これにより、ネットショップは公開鍵を「公開」し、顧客はそれを用いて個人情報を暗号化して送ることにすると、第三者に勝手に見られたり、盗まれる危険がありません。
RSA暗号の開発によって、このような公開鍵暗号が一般的に使われるようになりました。
RSA暗号の原理
上記のことを数学で表現すると次のようになります。
- 受信者が公開鍵を作る。
- 十分大きな2つの素数\(p,q\ (p\neq q)\)を選び、\(n=pq\)として、\(n\)から\(p\)と\(q\)を計算することが実用上必要な時間にできない(例えば数百年とか)ようにする。
-
\(e\)と\(\varphi(n)\)が互いに素であるような\(2\)以上の整数\(e\)を求める。
ただし、
\(\varphi(n)=|\{i\in\mathbb{Z}|1\leq i\leq n, i\)と\(n\)は互いに素\(\}|\)とします。
- 送信者は受信者の公開鍵を取得する。
- 暗号化したいメッセージを送信者が公開鍵を使って暗号化し、送信する。 \(n\)よりも小さい正の整数\(A\)を送るとします。
- 受信者が暗号化されたメッセージを受け取る。
- 受信者は暗号文を秘密鍵で暗号化する前のメッセージに復号化する。 \(ed\equiv1\ ({\rm mod}\ \varphi(n))\)を満たす正の整数\(d\)を求めます。
\(A^\prime\equiv A^e\ ({\rm mod}\ n)\)となる\(A^\prime\)を計算します(\(A^e\)を\(n\)で割った余りが\(A^\prime\))。
この\(A^\prime\)を暗号として受信者に送信します。
この\(d\)が暗号を復号化するための鍵、すなわち秘密鍵です。
すると、\(A\equiv\left( A^\prime\right)^d\ ({\rm mod}\ n)\)が成り立つため、\(A\)が分かる、ということです。
皆様のコメントを下さい！
整数論は、ガウスをして「数学の女王である」と言わしめた分野です。
整数論に限らず、皆様が「これ、面白いわ」と思った分野や問題がありましたらぜひコメントで教えて下さい！
結
今回は、初等整数論に入る前に、初等整数論のモチベーションとその応用例を軽く説明しました。
個人的な整数論が面白いと思う理由は
- 主張自体はシンプルなのに、いざ真偽を確かめようとすると難しい
- 発想力が問われる
です。
本ブログを読んでいただいている方ならおわかりかと思いますが、【１時間チャレンジシリーズ】で筆者が整数論の問題が苦手ということはご存知だと思います(笑)。
苦手ですが、結構好きなんですね。
次回からいよいよ初等整数論の内容に入っていきます。
乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ１週間以内にお答えします。
(難しかったらもう少しかかるかもしれませんが…)
初等整数論について、以下の書籍をオススメします！
コメントをする