本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回は「エレガントな解答をもとむ selections」に掲載されいている問題です。
では、問題
今回は前回の最後に「皆様への挑戦状」ということで提示した問題です。
力学に関係する問題です。
太郎君がこう言いました。「太陽から地球に光が届くには\(8\)分ほどかかる。地平線に太陽が沈んだと見えるときには実際の太陽の位置は\(8\)分ほど進んだ地平線の下の方にあるんだ。」
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p12.
次郎君は「へー、なるほど」と言ってちょっと考えていましたが、「本当にそうなのかなあ」と少し疑問があるようです。
太郎君が正しいのか次郎くんが正しいのか、読者の明快でエレガントな説明を求めます。
いざ、チャレンジ
チャレンジの結果…..「まあ解けただろう」という中途半端な感じです。
「間違ってはいないだろう」という感じです。
「間違ってはいないが、出題者の意図には答えていない」というのが正しい表現かもしれません。
筆者の解答
筆者の解答としては
です。
まずは、太郎君の主張が本当に正しいのかを確認してみました。
公益社団法人日本天文学会が公開している天文学辞典を参照したところ、
- 地球-太陽間の平均距離は約1億5000万km(\(=1.5\times10^8[{\rm km}]\))、
- 光速\(=299792458[{\rm m/s}]\)(約\(300000[{\rm km/s}]=3.0\times10^5[{\rm km/s}]\))
だそうです。
これを元に太陽光が地球に届くまでの時間を計算すると、
$$
\frac{1.5\times10^8}{3.0\times10^5}[{\rm s}]=0.5\times10^3[{\rm s}]=500[{\rm s}]=8.33\cdots[{\rm m}]
$$
です。
\(0.33\cdots[{\rm m}]\)が太郎君の主張の「\(8\)分ほど」の”ほど”に含まれるのであれば、太郎君の主張は概ね正しいということになります。
しかしあくまで地球と太陽の間の距離が\(1.5\times10^8[{\rm km}]\)で一定であるときの話です。
高校の物理の授業でケプラーの法則を習ったときに「地球の公転軌道は楕円である」と習いました。
もしこれが正しければ(正しいのですが)、地球と太陽の間の距離は一定ではありません。
従って、太郎君の主張は正しくないと予想できます。
しっかり論破するために「地球の公転軌道は本当に楕円軌道なのか」を語ることにしました。
ここで、太郎君と次郎君の会話を思い出し、「太郎君と次郎君の年齢はどのくらいだろうか」と思いました。
「もしかしたら小学生くらいの可能性もあるけど、あの会話だけから年齢を空いてするのは難しい」と思ったのでこのまま進んでみることにしました。
\(r(t)\)を時間\(t\)に依存する地球-太陽間の距離を表す関数、\(\theta(t)\)を時間に依存する角の方向の変化量を表す関数とします。
また、地球の質量を\(m\)とします。
このとき、地球の運動方程式は
\begin{eqnarray}
\begin{cases}
\displaystyle m\left(\frac{d^2r}{dt^2}-r\frac{d\theta}{dt}\right)=-\frac{K}{r^2}\\
\displaystyle \frac{m}{r}\frac{d}{dt}\left( r^2\frac{d\theta}{dt}\right)=0
\end{cases}
\end{eqnarray}
となります。
ただし、\(K\)は定数です。
また、2つめの式から\(\displaystyle r^2\frac{d\theta}{dt}=C\)です(\(C\)も定数)。
この運動方程式をに対して、\(\displaystyle\frac{1}{r}=p\)としてうまく計算すると
$$
mC^2\frac{d^2p}{d\theta^2}=-mC^2p+K
$$
です。
これは単振動の運動方程式なので、
$$
p=\frac{K}{mC^2}+A\cos\theta
$$
と解くことができます。
ただし、\(A\)は初期条件から定まる定数です。
$$
r=\frac{\displaystyle\frac{mC^2}{K}}{\displaystyle1+\frac{mC^2A}{K}\cos\theta}
$$
となります。
これはまさに楕円の極座標表示となっています。
故に、地球は太陽の周りを楕円軌道でもって公転しています。
あとは各定数が分かれば夏至、冬至のときの地球、太陽間の距離を割り出すことができるため、それでもって夏至、冬至のときの太陽の光が地球に到達するまでの時間を計算することができます。
しかし、定数は見つけられませんでした。
計算によって割り出すことができなくもないのでしょうが、1時間では足りませんでした。
そこで、先の天文学辞典で調べたところ、地球と太陽の間の距離が最も近いときと、最も遠いときの差は500万\([{\rm km}]\)程度だそうです。
「500万\([{\rm km}]\)が”程度”?」と思いましたが、地球-太陽間の平均距離から見るに距離の変化は\(\pm2\%\)ほどのようです(地球の公転軌道って殆ど円なんですね)。
500万\([{\rm km}]=5000000[{\rm km}]=5.0\times10^6[{\rm km}]\)なので、
$$
\frac{5.0\times10^6}{3.0\times10^5}[{\rm s}]=\frac{50}{3}[{\rm s}]=16.66\cdots[{\rm s}]=0.277\cdots[{\rm m}]
$$
です。
つまり、夏至、冬至での太陽光の到達時間の差が\(0.277\cdots[{\rm m}]\)ということになります。
太郎君の「8分ほど」の”ほど”に\(0.277\cdots[{\rm m}]\)が含まれるのなら、太郎君の主張は正しいですが、そもそも地球の公転軌道は円ではなく楕円ですので、次郎君が正しい、と結論づけました。
投稿されたエレガントな解答
では、投稿された解答を紹介します。
太陽から地球へ光が届くのに「8分ほどかかる」(正確には8分19秒)と書いたように、子の問題は精密な計算式や相対性理論を持ち出すことがねらいではありません。太郎くんと次郎くんお対話がこの調子で進んでいくうちに、小学校高学年の子でもなるほどと納得するような解答が出題者の意図した「エレガントな解答」でした。
とはいうものの、実は待機による太陽光の屈折の影響はばかにならないほど大きく、太陽の上縁が時間にして2分ほどの地平線の下にあってもまだ見える計算になります。(中略)
この問題は数学の問題ではなく、解釈の問題といえるような側面もあります。だから「正解」というのも少し書きにくいのですが、あえてポイントを示しておきましょう。光の屈折は考えないことにします。
「太郎くんの説は天動説を仮定すれば正しい。しかし、地動説を取れば太陽はまさに見えている方向に存在する。いま見ている光はたしかに約8分前の太陽の光だが、太陽は動かないのだから、光が北方向に太陽があるのは当然」
基本的にこのことに言及してある解答はすべて正解としました。厳密なことを言うと、観測や同時性の問題があるのでしょうが、「8分ほど」という言い回しに全てが吸収されてしまいます。どうしても光速や相対論が気になるのでしたら、次のような問題に言い換えてみたらどうでしょう。
「暗闇で回転木馬に載っていたら、突然山賊の矢が飛んできた。こちらはレーザー光線銃を持っている。どの方向に打ち返せばよいか」
山賊がジッとしているのであれば、明らかに屋の飛んできた方向へ打ち返すべきです。ところが、山賊が素早く動いているのであれば、メクラ撃ちしかないでしょう。ただし、山賊脳がゴキが予測可能なのであれば、夜の彷徨と速度から位置を逆算することが可能です。
「でも」という疑問を持たれた解答者が何人かいらっしゃいました。つまり、天動説・地動説どちらも太陽と地球の相対的運動の観点を変えただけなににどうして結論が違うのかというわけです。これはなんとなく人心を惑わす疑問ですが、座標系を変えて良いのは、等速直線運動をしている完成形だけであることに注意して下さい。たとえば、宇宙の中ですれ違う2台の等速度の宇宙船の撃ち合いを考えてみましょう。矢が飛んできたときに相手がどの方向にいるかは、どちらの宇宙船が停止していると考えてもお暗示結論になります。しかし、回転している系はだめです。(太陽系自身も宇宙の中の大きな回転運動に巻き込まれているのでしょうが、近似的に等速直線運動をしているとしても構わないでしょう。)さて、面白かった解答を紹介しましょう。どれも、太陽が動かないことを前提としています。
(1)日没の一瞬前に「地球よ止まれ」という呪文をかける。それからも太陽の上縁は見え続けるはず。もし、そのときに太陽が8分ほど地平線の下に進んだ位置にあれば、そのうち光は届かなくなる。これは矛盾。(中略)
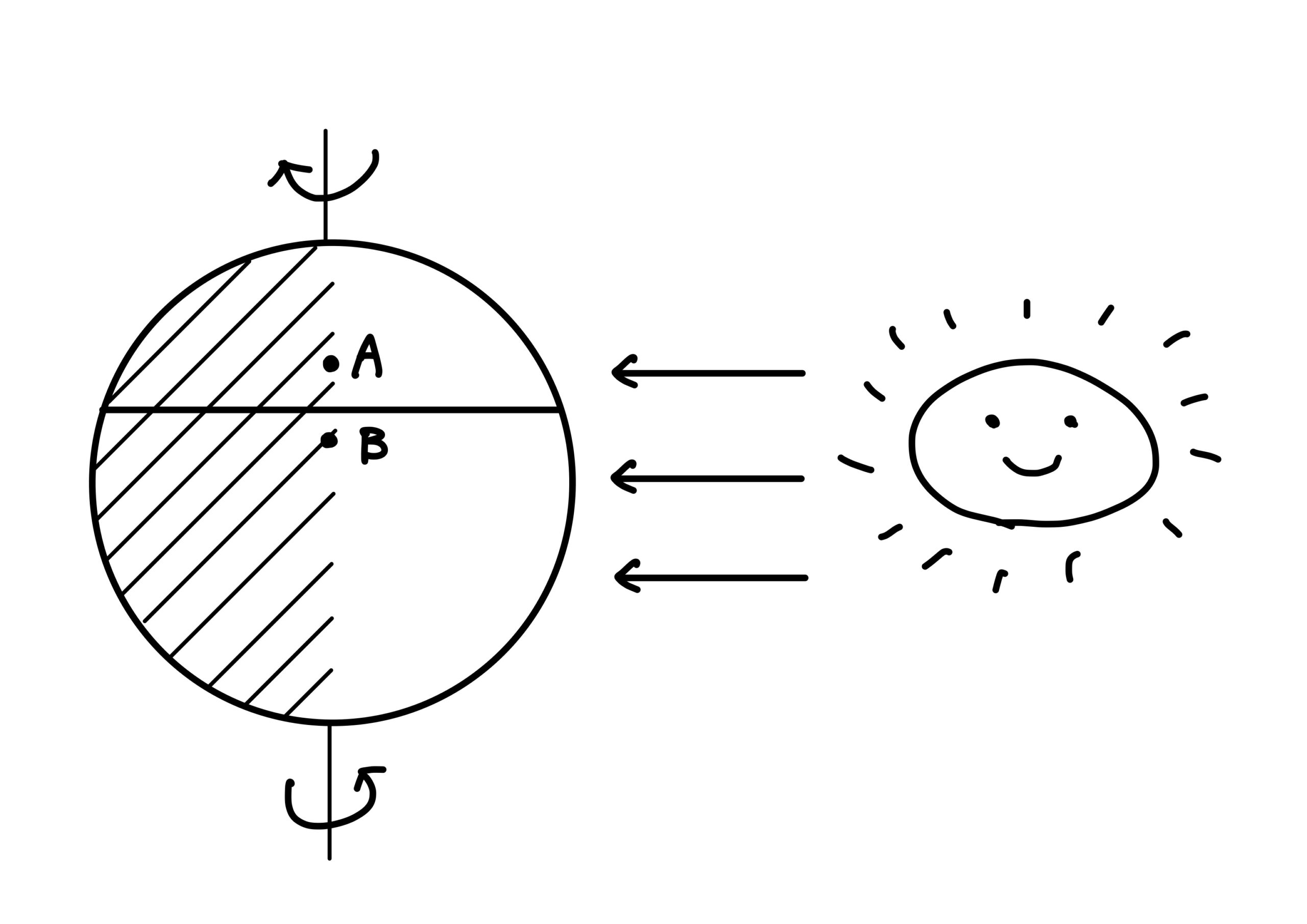
(2)日没の観測点を通る緯度で、地球を南北に切り(!)、南半球は北半球と逆の自転をさせる(図1)。切れ目のすぐ来たと南に観測者AとBがいたとし、Aが日没を観測する瞬間にBとバッタリ顔を合わせるものとしよう。このときBは日の出を観測する。Aが日没を見るときに太陽が地平線の下にあるとすると、Bはまだ地平線の下にある太陽の日の出を見ることになって矛盾。
(後略)
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p77-p79.
どうやら運動方程式を立てて計算するなどというのは、出題者の意図ではないようで…
(2)の解答はすごいな、と思いました。
発想というのでしょうか、地球を切って上下で逆回転させるというのは全くすごいですね。
筆者の解答は間違ってはないと思うのですが…どうでしょう?
皆様、コメントでご意見をいただけると嬉しいです。
読者の皆様への挑戦状!
今から紹介する問題の解答は来週解説します!
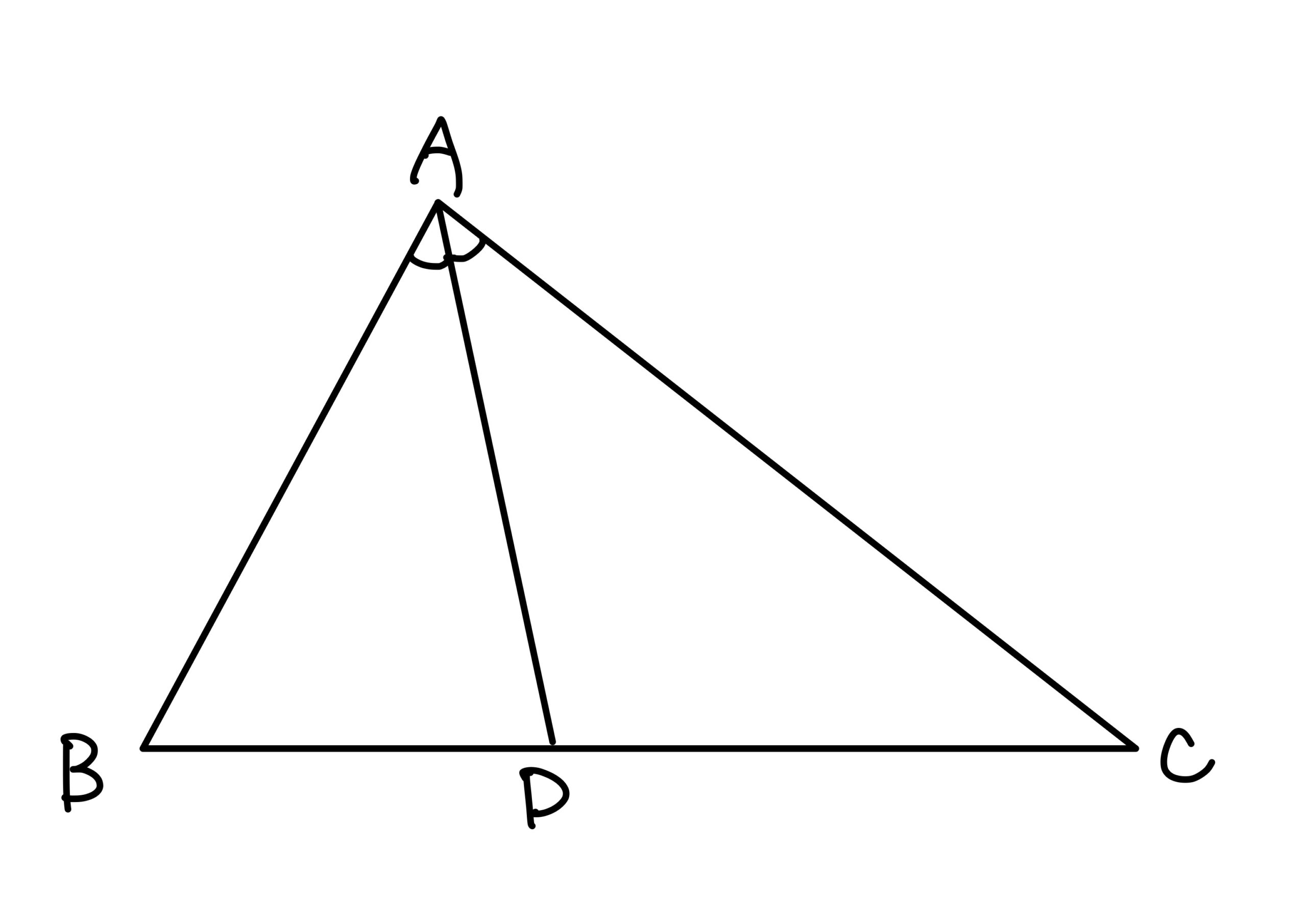
\(\triangle ABC\)の\(\angle A\)の2等分線と\(BC\)の交点を\(D\)とするとき
$$
AB+AD=CD,\quad AC+AD=BC
$$
であるという。\(\angle B\)、\(\angle C\)はどんな角か求めてください。数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p13.
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
今回の問題は「解けた!」と言い切れない感じが歯がゆかったです。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!



コメントをする