本記事の内容
本記事は線型独立(一次独立)と線型従属(一次従属)について解説する記事です。
本記事を読むにあたり、線型空間について知っている必要があるため、以下の記事も合わせてご覧ください。
線型独立と線型従属は重要です。
線型独立と線型従属は線型空間を語る上で避けては通れないものです。
というのも、線型空間の”風貌”を知るために誠に有用だからです。
「”風貌”って何よ?」という話ですが、線型独立なベクトルは(厳密には基底ですが)ある種の座標軸の役割を担っているからです(これについては後述します)。
それにつながる事実が以下です。
定理0.
\(V\)を線型空間、\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\)が線型独立であるとする。このとき、次の1.および2.は同値である。- \(\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\)が線型独立である。
- \(\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\)の線型結合で表される要素の表し方は一意的である。 すなわち、 $$ c_1\boldsymbol{a}_1+\dots+c_n\boldsymbol{a}_n=c_1^\prime\boldsymbol{a}_1+\dots+c_n^\prime\boldsymbol{a}_n $$ ならば、\(c_1=c_1^\prime,\dots.c_n=c_n^\prime\)である。
要するに、
と言っているわけです。
鋭い方は「なるほど。だから座標軸か。」と思うかもしれません。
もしそうならなくても大丈夫。ちゃんと解説します。
前回(【線型代数学の基礎シリーズ】線型空間編 その1)で述べたように、線型空間の要素をベクトルと呼ぶのでしたが、ベクトルは必ずしも数の組を表しているわけではないのでした。
しかし、数の組、すなわち\(\mathbb{R}^n\)の要素はベクトルの最たる例ですので、「なんかとっつきにくいな」と思った方は、線型空間といわれたらば\(\mathbb{R}^n\)を思い浮かべて、そのつもりで読んで頂いて大いに結構です。
線型空間のチャラい復習
線型空間とは以下でした。
線型空間(ベクトル空間)
集合\(V\)が次の2条件Ⅰ.およびⅡ.を満たすとき、\(V\)を複素線型空間、複素ベクトル空間、\(\mathbb{C}\)上の線型空間(ベクトル空間)という。- 任意の\(\boldsymbol{x},\boldsymbol{y}\in V\)に対して、和と呼ばれる第三の\(V\)の要素(これを\(\boldsymbol{x}+\boldsymbol{y}\in V\)と書く)が定まり、次の法則が成り立つ。
- \((\boldsymbol{x}+\boldsymbol{y})+\boldsymbol{z}=\boldsymbol{x}+(\boldsymbol{y}+\boldsymbol{z})\quad\)(結合則)
- \(\boldsymbol{x}+\boldsymbol{y}=\boldsymbol{y}+\boldsymbol{x}\quad\)(交換則)
- 零ベクトルと呼ばれる特別な要素(これを\(\boldsymbol{0}\)で表す)がただ1つ存在して、任意の\(\boldsymbol{x}\in V\)に対して\(\boldsymbol{0}+\boldsymbol{x}=\boldsymbol{x}\)が成り立つ。
- 任意の\(\boldsymbol{x}\in V\)に対して、\(\boldsymbol{x}+\boldsymbol{x}^\prime=\boldsymbol{0}\)となる\(\boldsymbol{x}^\prime\in V\)がただ1つ存在する。これを\(\boldsymbol{x}\)の逆ベクトルといい、\(-\boldsymbol{x}\)で表す。
- 任意の\(x\in V\)と任意の\(c\in\mathbb{C}\)に対して、\(\boldsymbol{x}\)の\(c\)倍と呼ばれるもう1つの\(V\)の要素(これを\(c\boldsymbol{x}\in V\)で表す)が定まり、次の法則が成り立つ、
- 任意の\(c,d\in\mathbb{C}\)に対して\((c+d)\boldsymbol{x}=c\boldsymbol{x}+d\boldsymbol{x}\)
- \(c(\boldsymbol{x}+\boldsymbol{y})=c\boldsymbol{x}+c\boldsymbol{y}\)
- 任意の\(c,d\in\mathbb{C}\)に対して、\((cd)\boldsymbol{x}=c(d\boldsymbol{x})\)
- \(1\boldsymbol{x}=\boldsymbol{x}\)
詳しくは【線型代数学の基礎シリーズ】線型空間編 その1を御覧ください。
線型独立と線型従属
では、線型独立と線型従属について解説します。
線型関係(一次関係)
まずは線型関係というものを解説します。
簡単です。
線型関係(一次関係)
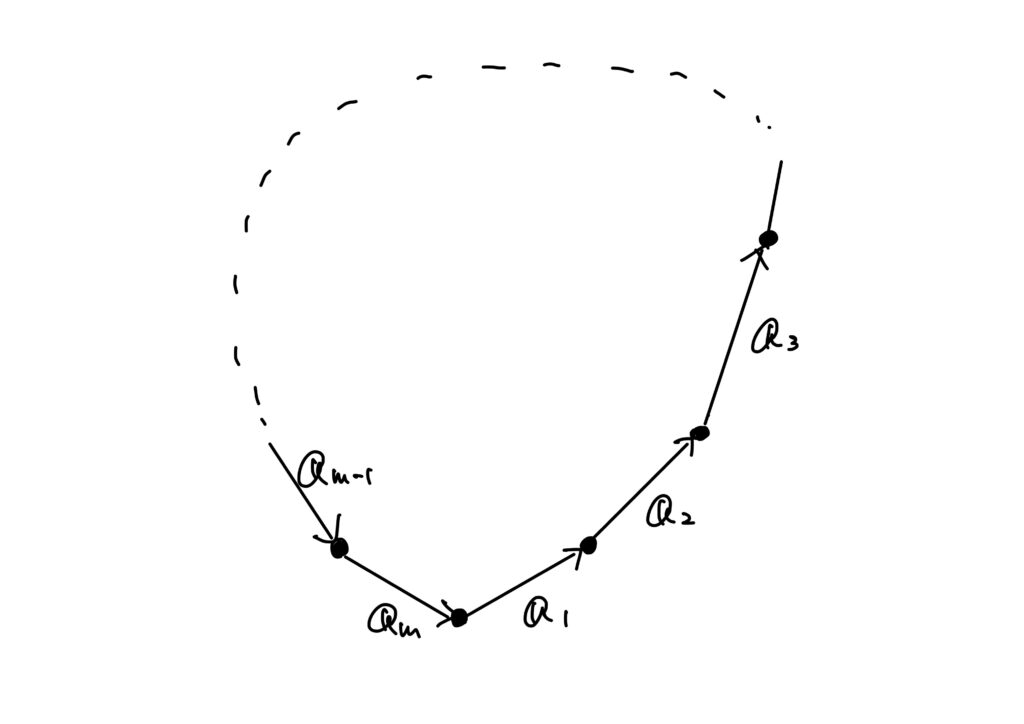
\(V\)を線型空間とする。\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m\in V\)が $$ c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+\dots+c_m\boldsymbol{a}_m=\boldsymbol{0}\quad (c_i\in\mathbb{R}) $$ を満たすとき、これをベクトル\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m\)の線型関係または一次関係という。任意の\(c_i\in\mathbb{R}\)が\(0\)のとき、 $$ 0\boldsymbol{a}_1+0\boldsymbol{a}_2+\dots+0\boldsymbol{a}_m=\boldsymbol{0} $$ はどんな\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m\)について成り立つ。これを自明な線型関係(一次関係)という。
あえてイメージをサラッと述べれば、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m\)のそれぞれを定数倍して和を取れば、ぐるっと回って\(\boldsymbol{a}_1\)のスタート地点に戻ってくる、といった具合です。
線型独立(一次独立)
線型独立を一言で言えば、
ということです。
要するに、ベクトルの組を\(0\)以外のどんな定数倍をして和をとってもグルっと回ってこない、ということが線型独立です。
そもそも定数が\(0\)だったらグルっと回るというイメージには即しません。
これをしっかり書くと以下です。
線型独立(一次独立)
\(V\)を線型空間とする。\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m\in V\)について、線型関係 $$ c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+\dots+c_m\boldsymbol{a}_m=\boldsymbol{0} $$ が成り立つのは、自明な線型関係、すなわち\(c_1=c_2=\dots=c_n=0\)の場合のみであるとき、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m\)は線型独立または一次独立であるという。例については線型従属とまとめて紹介します。
線型従属(一次従属)
線型従属はもう、一言で終いです。
単にこれだけです。
しっかり書くと以下です。
線型従属(一次従属)
\(V\)を線型空間とする。ベクトルの組\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m\)が線型独立でないとき、線型従属または一次従属であるという。すなわち、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m\)が線型従属であるとは、線型関係 $$ c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+\dots+c_m\boldsymbol{a}_m=\boldsymbol{0} $$ を満たす\(c_1,c_2,\dots,c_m\)で、そのうちの少なくとも1つが\(0\)でないものが存在するときにいう。どんなのが線型独立?線型従属?
例1.線型空間\(\mathbb{R}^3\)のベクトル
$$
\boldsymbol{a}_1=
\left(\begin{array}{c}
3\\
1\\
2\\
\end{array}\right),\quad
\boldsymbol{a}_2=
\left(\begin{array}{c}
2\\
1\\
1\\
\end{array}\right),\quad
\boldsymbol{a}_3=
\left(\begin{array}{c}
1\\
2\\
-1\\
\end{array}\right)
$$
について、\(\{\boldsymbol{a}_1,\boldsymbol{a}_2\}\)、\(\{\boldsymbol{a}_2,\boldsymbol{a}_3\}\)、\(\{\boldsymbol{a}_3,\boldsymbol{a}_1\}\)はそれぞれ線型独立で、\(\{\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3\}\)は線型従属です。
簡単に確かめられますので、\(\{\boldsymbol{a}_1,\boldsymbol{a}_2\}\)が線型独立であることと、\(\{\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3\}\)が線型従属であることのみを示すことにします。
①\(\{\boldsymbol{a}_1,\boldsymbol{a}_2\}\)が線型独立であること
確かめることとしては、
$$
c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2=\boldsymbol{0}
$$
のときに、\(c_1=c_2=0\)を示したいわけです。
故に、
$$
c_1
\left(\begin{array}{c}
3\\
1\\
2\\
\end{array}\right)+c_2
\left(\begin{array}{c}
2\\
1\\
1\\
\end{array}\right)
=
\left(\begin{array}{c}
0\\
0\\
0\\
\end{array}\right)\Leftrightarrow
\begin{cases}
3c_1+2c_2=0\\
c_1+c_2=0\\
2c_1+c_2=0
\end{cases}
$$
となるので、これを解くと、\(c_1=c_2=0\)が導けるので、線型独立です。
②\(\{\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3\}\)が線型従属であること
確かめることとしては
$$
c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+c_3\boldsymbol{a}_3=\boldsymbol{0}
$$
のときに、\(c_1=c_2=c_3=0\)以外の解があることです。
つまり、
$$
\begin{cases}
3c_1+2c_2+c_3=0\\
c_1+c_2+2c_3=0\\
2c_1+c_2-c_3=0
\end{cases}
$$
の解です。
これを解くと、
$$
5c_1=-3c_2,\quad 5c_3=-c_2
$$
となりますので、例えば\((c_1,c_2,c_3)=(3,-5,1)\)を解にもちます。
すなわち、
$$
3\boldsymbol{a}_1-5\boldsymbol{a}_2+\boldsymbol{a}_3=\boldsymbol{0}
$$
が成り立つので、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3\)は線型従属です。
線型独立、線型従属と部分空間
線型独立、線型従属と部分空間について説明します。
とはいえ「ふーん。そーなんだー。」程度でOKです。
これはやがてしっかりと証明されることです。
一言で述べれば、
です。
もう少し説明します。
ベクトルの組\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m\)が与えられたとき、これらによって生成される部分空間\(S[\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m]\)を考えます。
\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m\)によって生成される部分空間というのは
$$
S[\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m]
=\left\{x_1\boldsymbol{a}_1+x_2\boldsymbol{a}_2+\dots+x_m\boldsymbol{a}_m \middle| x_i\in\mathbb{R},\ i=1,2,\dots,r\right\}
$$
でした。
\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_m\)
からどの1個のベクトルを取り除いても生成する部分空間が小さくなってしまうときに、線型独立です。
一方で、あるベクトルを取り去っても生成する部分空間が変わりなく同じなのが線型従属です。
線型独立なベクトル、線型従属なベクトルと座標軸(チャラいイメージ)
チャラくイメージを解説します。
厳密な話は後の基底に関する記事で解説します。
線型独立なベクトルと座標軸
例2.平面上の\((1,2)\)という点について考えます。
これを標準基底
$$
\boldsymbol{e}_1=
\left(
\begin{array}{c}
1\\
0\\
\end{array}\right),\quad
\boldsymbol{e}_2=
\left(
\begin{array}{c}
0\\
1\\
\end{array}\right)
$$
を用いて表すと、
$$
\left(
\begin{array}{c}
1\\
2\\
\end{array}\right)=1\cdot
\left(
\begin{array}{c}
1\\
0\\
\end{array}\right)+2
\left(
\begin{array}{c}
0\\
1\\
\end{array}\right)
$$
です。
つまり、標準基底の係数が座標になっています。
これを図を描けば次です。

次のようなベクトルを考えてみます。
$$
\boldsymbol{a}_1=
\left(
\begin{array}{c}
-1\\
2\\
\end{array}\right),\quad
\boldsymbol{a}_2=
\left(
\begin{array}{c}
2\\
1\\
\end{array}\right)
$$
このとき、\(\boldsymbol{a}_1\)、\(\boldsymbol{a}_2\)は線型独立なベクトルで、
$$
\left(
\begin{array}{c}
1\\
2\\
\end{array}\right)=
\frac{3}{5}\boldsymbol{a}_1+\frac{4}{5}\boldsymbol{a}_2
$$
となります。
これを図で描くと次です。

つまり、\(\boldsymbol{a}_1\)と\(\boldsymbol{a}_2\)を伸ばした直線を座標軸にしたら、点\((1,2)\)の座標は\(\displaystyle\left( \frac{3}{5},\frac{4}{5}\right)\)ということになります。
言ってしまえば、そもそも座標軸は直角に交わる必要はないので、斜めに交わった直線を座標軸として考えても良いわけです。
従って、線型独立なベクトル(本当は基底ですが)は座標軸的な役割を担うことができます。
物理、特に力学を学んだ方は分かるかと思いますが、座標軸は基本的に好き勝手に取ってOKでした。
つまり、考える空間に対してより考えやすい座標軸を設定するときに、線型独立なベクトルというのは有用なのです。
線型従属と座標軸
一方で、線型従属なベクトルというのは座標軸になり得ないベクトルのことを指します。
例えば、次のような状況を考えてみます。
例3.
$$
\boldsymbol{a}_1=
\left(
\begin{array}{c}
3\\
4\\
\end{array}\right),\quad
\boldsymbol{a}_2=
\left(
\begin{array}{c}
6\\
8\\
\end{array}\right)
$$
とすると、\(\boldsymbol{a}_1\)、\(\boldsymbol{a}_2\)線型従属です(簡単な計算で確かめられます)。
このとき、平面上の点\((1,2)\)はベクトル\(\boldsymbol{a}_1\)、\(\boldsymbol{a}_2\)を用いて一意的に表現することはできません。
実際、
\begin{eqnarray}
\left(
\begin{array}{c}
1\\
2\\
\end{array}\right)&=&
1\cdot\left(
\begin{array}{c}
3\\
4\\
\end{array}\right)-\frac{1}{3}\cdot
\left(
\begin{array}{c}
6\\
8\\
\end{array}\right)\\
&=&
2\cdot\left(
\begin{array}{c}
3\\
4\\
\end{array}\right)-\frac{5}{6}\cdot
\left(
\begin{array}{c}
6\\
8\\
\end{array}\right)\\
\end{eqnarray}
です。
他にもたくさん有ります。
従って、座標が1つに定まりません。
故に\(\boldsymbol{a}_1\)、\(\boldsymbol{a}_2\)は座標軸にはなりえません。
さらに言えば、線型従属というのは、一方のベクトルがもう一方のベクトルの定数倍になっているときとも言いかえることができます。
今回の場合においては
$$
\left(
\begin{array}{c}
3\\
4\\
\end{array}\right)=2
\left(
\begin{array}{c}
6\\
8\\
\end{array}\right)
$$
です。
線型空間の任意の要素は線型独立なベクトルの線型結合で一意的に表される。
では、定理0.を証明しましょう。
定理0.を再掲します。
定理0.
\(V\)を線型空間、\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\)が線型独立であるとする。このとき、次の1.および2.は同値である。- \(\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\)が線型独立である。
- \(\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\)の線型結合で表される要素の表し方は一意的である。 すなわち、 $$ c_1\boldsymbol{a}_1+\dots+c_n\boldsymbol{a}_n=c_1^\prime\boldsymbol{a}_1+\dots+c_n^\prime\boldsymbol{a}_n $$ ならば、\(c_1=c_1^\prime,\dots.c_n=c_n^\prime\)である。
定理0.の証明
(1.\(\Rightarrow\)2.の証明)
2.の等式を移項します。
$$
(c_1-c_1^\prime)\boldsymbol{a}_1+\dots+(c_n-c_n^\prime)\boldsymbol{a}_n=\boldsymbol{0}
$$_
ここで、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n\)は仮定から線型独立ですので、
$$
c_1-c_1^\prime=\cdots=c_n-c_n^\prime=0
$$
です。
すなわち、
$$
c_1=c_1^\prime,\cdots,\ c_n=c_n^\prime
$$
となるので、表し方は一意的です。
(2.\(\Rightarrow\)1.の証明)
線型関係
$$
c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+\dots+c_n\boldsymbol{a}_n=\boldsymbol{0}
$$
を満たす\(c_i\)として、\(c_i=0\)があります。
しかし、仮定から、この表し方が一意的なので、\(c_i=0\)以外は存在しません。
従って、
$$
c_i=0\quad (i=1,\dots,n)
$$
が成り立ち、これは\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n\)が線型独立であることを指しています。
定理0.の証明終わり
線型独立、線型従属の基本的な性質
線型独立と線型従属の基本的な性質を紹介します。
定理4.
\(V\)を線型空間とする。\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\in V\)のうち、1つのベクトルが残りのベクトルの線型結合として表示できることと、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\in V\)が線型従属であることは同値である。また、どのベクトルも残りのベクトルの線型結合で表示できないことと、ベクトルの組\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)が線型独立であることは同値である。
先述した「線型従属なベクトルには余分なものがある」というのはこの事実が成り立つからです。
定理4.の証明
①「\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\in V\)のうち、1つのベクトルが残りのベクトルの線型結合として表示できる\(\Rightarrow\)\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\in V\)が線型従属である」の証明
\(\boldsymbol{a}_1\)が他の残りのベクトルの線型結合で表示できたとしましょう。
このとき、
$$
\boldsymbol{a}_1=c_2\boldsymbol{a}_2+\dots+c_r\boldsymbol{a}_r
$$
と書いたとします。
この式の右辺を移項すると
$$
1\cdot\boldsymbol{a}_1+(-c_2)\boldsymbol{a}_2+\dots+(-c_r)\boldsymbol{a}_r=\boldsymbol{0}
$$
となります。
これを見ると、\(\boldsymbol{a}_1\)の係数は\(1\)ですので、\(c_1\neq0\)ですから線型従属です。
\(\boldsymbol{a}_1\)以外のベクトル\(\boldsymbol{a}_i\)が他のベクトルの線型結合として表示できる場合も全く同じに証明できます。
②「\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\in V\)が線型従属である\(\Rightarrow\)\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\in V\)のうち、1つのベクトルが残りのベクトルの線型結合として表示できる」の証明
\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)が線型従属だとします。
すると、線型関係の式
$$
c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+\dots+c_r\boldsymbol{a}_r=\boldsymbol{0}
$$
で少なくとも1つの\(c_i\)が\(0\)でないということになります。
例えばそれを\(c_1\)としましょう。
そのとき、\(c_1\neq0\)なので、\(c_1\)で上記の線型関係の式を割ることができます。
故に
$$
\boldsymbol{a}_1=\left(-\frac{c_2}{c_1}\right)\boldsymbol{a}_2+\dots+\left(-\frac{c_r}{c_1}\right)\boldsymbol{a}_r
$$
となります。
従って、\(\boldsymbol{a}_1\)が他の残りのベクトルの線型結合で表されました。
\(0\)でない係数が\(c_1\)でない場合も全く同じです。
③「どのベクトルも残りのベクトルの線型結合で表示できないことと、ベクトルの組\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)が線型独立であることは同値である。」の証明
①、②によって①\(\Leftrightarrow\)②が証明されたので、③はこの対偶ですから、成り立ちます。
定理4.の証明終わり
定理5.
\(V\)を線型空間とする。\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_s\in V\)に対して- \(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\ (r<s)\)が線型従属であれば、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_s\)も線型従属である。
- \(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_s\)が線型独立であれば、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\ (r<s)\)も線型独立である。
とどのつまり、線型従属なベクトルに、ベクトルを増やしても線型従属だし、線型独立なベクトルからベクトルを減らしても線型独立だ、ということです。
定理5.の証明
(1.の証明)
\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)が線型従属だとすると、
$$
c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+\dots+c_r\boldsymbol{a}_r=\boldsymbol{0}
$$
のとき、少なくとも1つの\(c_i\)が\(0\)ではありません。
故に
$$
c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+\dots+c_r\boldsymbol{a}_r+0\cdot\boldsymbol{a}_{r+1}+\dots+0\cdot\boldsymbol{a}_s=\boldsymbol{0}
$$
という線型関係についても\(c_1\)から\(c_r\)の中に\(0\)でないものが存在しますので、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_s\)は線型従属です。
(2.の証明)
といっても、2.は1.の対偶ですので、成り立ちます。
定理5.の証明終わり
定理6.
\(V\)を線型空間とする。\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)が線型独立で、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r,\boldsymbol{a}\)が線型従属であれば、\(\boldsymbol{a}\)は\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)の線型結合として一意的に表される。先に述べた「線型独立なベクトルには無駄なものが無い」というのはこれが成り立つからです。
定理6.の証明
\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r,\boldsymbol{a}\)が線型従属だとします。
このとき、線型関係
$$
c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+\dots+c_r\boldsymbol{a}_r+c\boldsymbol{a}=\boldsymbol{0}
$$
の\(c_1,c_2,\dots,c_r,c\)の中で\(0\)でないものが存在します。
もし仮に\(c=0\)であれば\(c\)以外の\(c_1,c_2,\dots,c_r\)の中に\(0\)となるものが存在しますが、
$$
c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+\dots+c_r\boldsymbol{a}_r=\boldsymbol{0}
$$
となって、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)が線型独立なので、\(c_1=c_2=\dots=c_r=0\)に矛盾です。
従って、\(c\neq0\)でなければなりません。
このとき、
$$
\boldsymbol{a}=-\frac{c_1}{c}\boldsymbol{a}_1-\frac{c_2}{c}\boldsymbol{a}_2-\dots-\frac{c_r}{c}\boldsymbol{a}_r
$$
となるので、\(\boldsymbol{a}\)は\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)の線型結合で表されます。
次に一意性です。
今、\(\boldsymbol{a}\)が\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)の線型結合として
$$
\boldsymbol{a}=c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+\dots+c_r\boldsymbol{a}_r=c_1^\prime\boldsymbol{a}_1+c_2^\prime\boldsymbol{a}_2+\dots+c_r^\prime\boldsymbol{a}_r
$$
の2通りで書かれたとします。
この等式を移項すると、
$$
(c_1-c_1^\prime)\boldsymbol{a}_1+(c_2-c_2^\prime)\boldsymbol{a}_2+\dots+(c_r-c_r^\prime)\boldsymbol{a}_r=\boldsymbol{0}
$$
となりますが、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r\)が線型独立なので、
$$
c_1-c_1^\prime=c_2-c_2^\prime=\dots=c_r-c_r^\prime=0
$$
すなわち、
$$
c_1=c_1^\prime,\ c_2=c_2^\prime,\ \dots,\ c_r=c_r^\prime
$$
となるので、一意性が証明できました。
定理6.の証明終わり
結
今回は、線型独立、線型従属とその基本的な性質を解説しました。
一言で言えば、線型独立と線型従属とは
ということでした。
そして、線型独立なベクトルから次回の基底の概念が出現して、基底により線型空間の風貌を捉えやすくなります。
次回は基底と線型空間の次元について解説します。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする