本記事の内容
本記事はグラム-シュミットの正規直交化法について解説して、実際に三角化を計算してみる記事です。
本記事を読むにあたり、行列の対角化、三角化について知っている必要があるため、以下の記事も合わせてご覧ください。
↓対角化の記事
↓三角化の記事
また、直交行列、ユニタリ行列についても知っている必要があるので、以下の記事も合わせてご覧ください。
三角化をエクストリームに復習
三角化についてエクストリームに復習します。
三角化に似たものとして対角化があります。
しかし、どんな行列も対角化できる、というわけではありません。
そこで、条件を少し緩めて「対角行列にはできずとも、三角行列にはできるんじゃないか?」というコンセプトが三角化です。
定理1.
\(n\)次正方行列\(A\)が、重複も含めて\(n\)個の固有値\(\lambda_1,\dots,\lambda_n\)をもつとき(すなわち、\(\varphi_A(t)=(\lambda_1-t)\cdots(\lambda_n-t)\)となるとき)、\(A\)は適当な正則行列\(P\)によって次の形に三角化される。 $$ P^{-1}AP= \begin{pmatrix} \lambda_1&&&\huge{*}\\ &\lambda_2&&\\ &&\ddots&\\ \huge{O}&&&\lambda_n \end{pmatrix} $$ここで、「重複を込めて\(n\)個の固有値を持てば…」という仮定に注目してみます。
「じゃあ固有値を持たない行列については三角化できない行列もあんのね?」となるわけですが、実は、\(n\)次正方行列の固有値を複素数の範囲まで許すと、必ず重複を込めて\(n\)個の固有値を持つので、複素数の範囲では必ず三角化ができるということになります。
ある正方行列に固有値が存在して、しかもそれがすべて実数であれば、直交行列でもって三角化できます。
もしその固有値が複素数であれば、直交行列の複素数バージョンであるユニタリ行列でもって三角化できます。
上記の直交行列とユニタリ行列をどうやって見つけてくるのか、という話ですが、それは固有ベクトルを並べてできる行列として見つけてくる、ということでした。
しかしながら、単に固有ベクトルを並べても必ずしも直交行列にはなりません。
従って、固有ベクトルを用いて直交するようなベクトルを見つけてくる必要があります。
そこで活躍するのがグラム-シュミットの正規直交化法なのです。
内積空間
まずは、「そもそも内積って?」というところから話を始めます。
標準的な内積、自然な内積
我々がよく知っている内積は線型空間\(\mathbb{R}^n\)の任意の\(\boldsymbol{a},\boldsymbol{b}\in\mathbb{R}^n\)に対して\(\displaystyle
\boldsymbol{a}=\left(
\begin{array}{c}
a_1\\
\vdots\\
a_n\end{array}\right)
\)、\(\displaystyle
\boldsymbol{b}=\left(
\begin{array}{c}
b_1\\
\vdots\\
b_n\end{array}\right)
\)と書いたとき、
$$
a_1b_1+\dots+a_nb_n
$$
を\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の内積と言って、\((\boldsymbol{a},\boldsymbol{b})\)で表したものでした。
写像の言葉を使うと、\(\boldsymbol{a}\)と\(\boldsymbol{b}\)に対して、実数\((\boldsymbol{a},\boldsymbol{b})\)を対応させる写像
$$
(\ ,\ ):\mathbb{R}^n\times\mathbb{R}^n\to \mathbb{R}
$$
を\(\mathbb{R}^n\)の内積といいます。
この方法で定めた内積を\(\mathbb{R}^n\)の標準的な内積、または自然な内積といいます。
え?内積ってこれだけじゃないの?じゃあ内積って何?
内積は先程あげたものだけではありません。いっぱいあります。
先の標準的な内積はあくまで内積の一例に過ぎないということです。
とはいえ、最もよく使われるな積ですが。
では、内積とは一体何者なのか、ということを厳密に語ります。
内積、計量線型空間
\(\mathbb{R}\)上の線型空間\(V\)において、任意の2つのベクトル\(\boldsymbol{a}\)および\(\boldsymbol{b}\)に対して、実数\((\boldsymbol{a},\boldsymbol{b})\)が定まり、次の1.〜4.を満たすときに、\((\boldsymbol{a},\boldsymbol{b})\)を\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の内積という。- \(\left(\boldsymbol{a},\boldsymbol{b}\right)=\left(\boldsymbol{b},\boldsymbol{a}\right)\)
- \(\left(\boldsymbol{a}+\boldsymbol{b},\boldsymbol{c}\right)=\left(\boldsymbol{a},\boldsymbol{c}\right)+\left(\boldsymbol{b},\boldsymbol{c}\right)\)
- \(\left(k\boldsymbol{a},\boldsymbol{b}\right)\quad (k\in\mathbb{R})\)
- \(\left(\boldsymbol{a},\boldsymbol{a}\right)\geq0\)で、\(\left(\boldsymbol{a},\boldsymbol{a}\right)=0\Leftrightarrow \boldsymbol{a}=\boldsymbol{0}\)
\(\mathbb{R}^n\)の標準的な内積は上記の4つの条件を満たすことが簡単に示されます。
内積というのは、線形空間に対して定められるコンセプトです。
従って、\(\mathbb{R}^n\)以外の線型空間についても内積を定めることができます。
余談(実はこんなのも内積)
$$ L^2(\mathbb{R})=\left\{fは\mathbb{R}上の複素数値可測関数\middle|\int_\mathbb{R}|f(t)|^2dt<\infty\right\} $$ としたとき、\(f,g\in L^2(\mathbb{R})\)に対して、 $$ (f,g)=\int_\mathbb{R}f(t)\overline{g(t)}\ dt $$ とすると、\((f,g)\)は内積です。「へえ。こんなのも内積なんだあ」くらいでOKです。ベクトルの長さ(ノルム)
今までさも当然のように「知ってるよね?」ということでベクトルの大きさを使ってきました。
しかし、本来はベクトルの大きさというのは計量線型空間\(V\)に定められる量です。
ベクトルの長さって何スか?
ベクトルのノルム
\(V\)を計量線型空間、\((\ ,\ )\)をその内積とする。このとき、\(V\)の任意のベクトル\(\boldsymbol{a}\)に対して、\(\sqrt{\left(\boldsymbol{a},\boldsymbol{a}\right)}\)をベクトル\(\boldsymbol{a}\)の長さ、またはノルム(norm)といって、\(\|\boldsymbol{a}\|\)で表す。すなわち、 $$ \|\boldsymbol{a}\|=\sqrt{\left(\boldsymbol{a},\boldsymbol{a}\right)},\quad \|\boldsymbol{a}\|^2=\left(\boldsymbol{a},\boldsymbol{a}\right) $$ である。ベクトルの長さに関する基本的な性質を調べてみましょう。
ベクトルの長さの基本的な性質
定理2.
計量線型空間\(V\)の\left(\boldsymbol{x},\boldsymbol{y}\right)と長さについて、次のことが成り立つ。 \(\boldsymbol{a},\boldsymbol{b}\in V\)、\(k\in\mathbb{R}\)とする。- \(\|\boldsymbol{a}\|\geq0\quad\)(等号は\(\boldsymbol{a}=\boldsymbol{0}\)のときに限り成り立つ)
- \(\|k\boldsymbol{a}\|=|k|\cdot\|\boldsymbol{a}\|\)
- \(\displaystyle\left(\boldsymbol{a},\boldsymbol{b}\right)=\frac{1}{2}\left\{\|\boldsymbol{a}+\boldsymbol{b}\|^2-\|\boldsymbol{a}\|^2-\|\boldsymbol{b}\|^2\right\}=\frac{1}{2}\left\{\|\boldsymbol{a}\|^2+\|\boldsymbol{b}\|^2-\|\boldsymbol{a}-\boldsymbol{b}\|^2\right\}\)
- \(\displaystyle\|\boldsymbol{a}+\boldsymbol{b}\|^2+\|\boldsymbol{a}-\boldsymbol{b}\|^2=2\left( \|\boldsymbol{a}\|^2+\|\boldsymbol{b}\|^2\right)\quad\)(中線定理)
定理2.の証明
(1.の証明)
\(\|\boldsymbol{a}\|^2=\sqrt{\left(\boldsymbol{a},\boldsymbol{a}\right)}\)と、内積が満たすべき条件の4.により、\(\|\boldsymbol{a}\|\geq0\)かつ、\(\|\boldsymbol{a}\|=0\)と\(\boldsymbol{a}=\boldsymbol{0}\)は同値です。
(2.の証明)
$$
\|k\boldsymbol{a}\|^2=\left(k\boldsymbol{a},k\boldsymbol{a}\right)=k^2\left(\boldsymbol{a},\boldsymbol{a}\right)=k^2\|\boldsymbol{a}\|^2
$$
なので、成り立ちます。
(3.の証明)
\begin{eqnarray}
\|\boldsymbol{a}+\boldsymbol{b}\|^2&=&\left(\boldsymbol{a}+\boldsymbol{b},\boldsymbol{a}+\boldsymbol{b}\right)\\
&=&\left(\boldsymbol{a},\boldsymbol{a}\right)+2\left(\boldsymbol{a},\boldsymbol{b}\right)+\left(\boldsymbol{b},\boldsymbol{b}\right)\\
&=&\|\boldsymbol{a}\|^2+2\left(\boldsymbol{a},\boldsymbol{b}\right)+\|\boldsymbol{b}\|^2
\end{eqnarray}
となるので、最後の式を変形して、
$$
\left(\boldsymbol{a},\boldsymbol{b}\right)=\frac{1}{2}\left\{\|\boldsymbol{a}+\boldsymbol{b}\|^2-\|\boldsymbol{a}\|^2-\|\boldsymbol{b}\|^2\right\}
$$
となります。
また、
\begin{eqnarray}
\|\boldsymbol{a}-\boldsymbol{b}\|^2&=&\left(\boldsymbol{a}-\boldsymbol{b},\boldsymbol{a}-\boldsymbol{b}\right)\\
&=&\left(\boldsymbol{a},\boldsymbol{a}\right)-2\left(\boldsymbol{a},\boldsymbol{b}\right)+\left(\boldsymbol{b},\boldsymbol{b}\right)\\
&=&\|\boldsymbol{a}\|^2-2\left(\boldsymbol{a},\boldsymbol{b}\right)+\|\boldsymbol{b}\|^2
\end{eqnarray}
となるので、最後の式を変形して、
$$
\left(\boldsymbol{a},\boldsymbol{b}\right)=\frac{1}{2}\left\{\|\boldsymbol{a}\|^2+\|\boldsymbol{b}\|^2-\|\boldsymbol{a}-\boldsymbol{b}\|^2\right\}
$$
となります。
(4.の証明)
先程得た式
$$
\|\boldsymbol{a}+\boldsymbol{b}\|^2=\|\boldsymbol{a}\|^2+2\left(\boldsymbol{a},\boldsymbol{b}\right)+\|\boldsymbol{b}\|^2\\
\|\boldsymbol{a}-\boldsymbol{b}\|^2=\|\boldsymbol{a}\|^2-2\left(\boldsymbol{a},\boldsymbol{b}\right)+\|\boldsymbol{b}\|^2
$$
の辺々を足し算して、求める式を得ます。
定理2.の証明終わり
ベクトルの直交
これは簡単で、内積\(=0\)のときを指します。
ベクトルの直交
計量線型空間\(V\)のwつのベクトル\(\boldsymbol{a},\boldsymbol{b}\)が $$ \left(\boldsymbol{a},\boldsymbol{b}\right)=0 $$ を満たすとき、\(\boldsymbol{a}\)と\(\boldsymbol{b}\)は直行するといい、\(\boldsymbol{a}\perp\boldsymbol{b}\)で表す。\(\boldsymbol{a}\)または\(\boldsymbol{b}\)が零ベクトルの場合、\(\left(\boldsymbol{a},\boldsymbol{b}\right)=0\)となるため、直交する場合に含める。すなわち、\(\boldsymbol{0}\)は任意のベクトルに直交するベクトルであると考える。
「うん。そう習ったよ。」という感じですよね。
ベクトルが直交していると、中学校で習った有名なPythagorasの定理を証明できます。
定理3.(Pythagoras)
\(\boldsymbol{a}\perp\boldsymbol{b}\)のとき、 $$ \|\boldsymbol{a}+\boldsymbol{b}\|^2=\|\boldsymbol{a}\|^2+\|\boldsymbol{b}\|^2 $$定理3.の証明
これはもうすでに証明しているようなもんです。
定理2.の3.の証明から
$$
\|\boldsymbol{a}+\boldsymbol{b}\|^2=\|\boldsymbol{a}\|^2+2\left(\boldsymbol{a},\boldsymbol{b}\right)+\|\boldsymbol{b}\|^2
$$
が成り立っていて、今\(\boldsymbol{a}\perp\boldsymbol{b}\)なのですから\(\left(\boldsymbol{a},\boldsymbol{b}\right)=0\)なので、
$$
\|\boldsymbol{a}+\boldsymbol{b}\|^2=\|\boldsymbol{a}\|^2+\|\boldsymbol{b}\|^2
$$
です。
定理3.の証明終わり
シュワルツの不等式
シュワルツの不等式は線型空間だけでなく、至るところで出現します。
定理4.(シュワルツの不等式)
任意の2つのベクトル\(\boldsymbol{a},\boldsymbol{b}\)に対して、 $$ |\left(\boldsymbol{a},\boldsymbol{b}\right)|\leq\|\boldsymbol{a}\|\cdot\|\boldsymbol{b}\| $$ が成り立つ。等号が成り立つのは\(\boldsymbol{a}=k\boldsymbol{b}\)または\(\boldsymbol{b}=k^\prime\boldsymbol{a}\)の形に書かれる場合に限る。ただし、\(k,k^\prime\in\mathbb{R}\)である。定理4.の証明
\(\boldsymbol{b}=\boldsymbol{0}\)のときは、両辺ともに\(0\)となるので、成り立ちます。
そこで、\(\boldsymbol{b}\neq\boldsymbol{0}\)とします。
このとき、\(\displaystyle k=\frac{\left(\boldsymbol{a},\boldsymbol{b}\right)}{\|\boldsymbol{b}\|^2}\)とすると、
\begin{eqnarray}
\|\boldsymbol{a}-k\boldsymbol{b}\|^2&=&\|\boldsymbol{a}\|^2-2k\left(\boldsymbol{a},\boldsymbol{b}\right)+k^2\|\boldsymbol{b}\|^2\\
&=&\|\boldsymbol{a}\|^2-\frac{2\left(\boldsymbol{a},\boldsymbol{b}\right)^2}{\|\boldsymbol{b}\|^2}+\frac{\left(\boldsymbol{a},\boldsymbol{b}\right)^2}{\|\boldsymbol{b}\|^2}\\
&=&\|\boldsymbol{a}\|^2-\frac{\left(\boldsymbol{a},\boldsymbol{b}\right)^2}{\|\boldsymbol{b}\|^2}
\end{eqnarray}
です。
ここで、\(\|\boldsymbol{a}-k\boldsymbol{b}\|^2\geq0\)なので、
$$
\|\boldsymbol{a}\|^2-\frac{\left(\boldsymbol{a},\boldsymbol{b}\right)^2}{\|\boldsymbol{b}\|^2}\geq0\Leftrightarrow \|\boldsymbol{a}\|\cdot\|\boldsymbol{b}\|\geq|\left(\boldsymbol{a},\boldsymbol{b}\right)|
$$
です。
仮に等号が成り立ったとすると、\(\boldsymbol{b}\neq0\)の場合、
$$
\|\boldsymbol{a}-k\boldsymbol{b}\|=0
$$
であり、すなわち\(\boldsymbol{a}=k\boldsymbol{b}\)のときです。
\(\boldsymbol{b}=\boldsymbol{0}\)の場合も等号が成り立つのですが、この場合\(\boldsymbol{b}=0\boldsymbol{a}\)と書けます。
従って、\(\boldsymbol{a}=k\boldsymbol{b}\)か\(\boldsymbol{b}=k^\prime\boldsymbol{a}\)と書かれます。
逆に、\(\boldsymbol{a}=k\boldsymbol{b}\)とすると、
$$
\|\boldsymbol{a}\|\cdot\|\boldsymbol{b}\|=|k|\|\boldsymbol{b}\|\cdot\|\boldsymbol{b}\|=|k|\|\boldsymbol{b}\|^2\\
|\left(\boldsymbol{a},\boldsymbol{b}\right)|=|\left(k\boldsymbol{b},\boldsymbol{b}\right)|=|k|\cdot|\left(\boldsymbol{b},\boldsymbol{b}\right)|=|k|\|\boldsymbol{b}\|^2
$$
となるので、等号が成り立ちます。
\(\boldsymbol{b}=k^\prime\boldsymbol{a}\)の場合も同様です。
定理4.の証明終わり
「本当かい?」と思われるかもしれませんので、簡単な例を挙げます。
例5. \(\displaystyle
\boldsymbol{a}=
\left(
\begin{array}{c}
1\\
2
\end{array}
\right),\
\boldsymbol{b}=
\left(
\begin{array}{c}
3\\
4
\end{array}
\right)
\)とします。
このとき、\(\left(\boldsymbol{a},\boldsymbol{b}\right)=1\cdot3+2\cdot4=3+8=11\)です。
一方で、\(\|\boldsymbol{a}\|=\sqrt{5}\)、\(\|\boldsymbol{b}\|=5\)により\(\|\boldsymbol{a}\|\cdot\|\boldsymbol{b}\|=5\sqrt{5}=11.18033.\cdots\)で、シュワルツの不等式が成り立ちます。
三角不等式
三角不等式も至るところで出現します。
定理6.(三角不等式)
任意の2つのベクトル\(\boldsymbol{a},\boldsymbol{b}\)に対して、 $$ \|\boldsymbol{a}+\boldsymbol{b}\|\leq\|\boldsymbol{a}\|+\|\boldsymbol{b}\| $$ が成り立つ。等号が成り立つのは、\(\boldsymbol{a}=k\boldsymbol{b}\ (k\geq0)\)、または\(\boldsymbol{b}=k^\prime\boldsymbol{a}\ (k^\prime\geq0)\)の場合に限る。定理6.の証明
シュワルツの不等式を使えばなんてことありません。
シュワルツの不等式から、
\begin{eqnarray}
\|\boldsymbol{a}+\boldsymbol{b}\|^2&=&\|\boldsymbol{a}\|^2+2\left(\boldsymbol{a},\boldsymbol{b}\right)+\|\boldsymbol{b}\|^2\\
&\leq&\|\boldsymbol{a}\|^2+2\|\boldsymbol{a}\|\|\boldsymbol{b}\|+\|\boldsymbol{b}\|^2\\
&=&\left( \|\boldsymbol{a}\|+\|\boldsymbol{b}\|\right)^2
\end{eqnarray}
となるので、
$$
\|\boldsymbol{a}+\boldsymbol{b}\|\leq\|\boldsymbol{a}\|+\|\boldsymbol{b}\|
$$
が成り立ちます。
等号はシュワルツの不等式において等号が成り立ち、かつ\(\left(\boldsymbol{a},\boldsymbol{b}\right)\geq0\)の場合なので、\(\boldsymbol{a}=k\boldsymbol{b},\ k\geq0\)または\(\boldsymbol{b}=k^\prime\boldsymbol{a},\ k^\prime\geq0\)の場合です。
定理6.の証明終わり
「本当かい?」と思われるかもしれませんので、簡単に例を挙げます。
先程の例5.を流用すると、
$$
\|\boldsymbol{a}+\boldsymbol{b}\|=
\left\|
\left(
\begin{array}{c}
4\\
6
\end{array}
\right)
\right\|=2\sqrt{13}
$$
であり、一方で、\(\|\boldsymbol{a}\|=\sqrt{5}\)、\(\|\boldsymbol{b}\|=5\)により、
$$
\|\boldsymbol{a}+\boldsymbol{b}\|=2\sqrt{13}=7.211102\cdots\\
\|\boldsymbol{a}\|+\|\boldsymbol{b}\|=5+\sqrt{5}=7.236067\cdots
$$
となるので、三角不等式が成り立ちます。
グラム-シュミットの正規直交化法
では、本記事の本題に入っていきます。
グラム-シュミット(ぐらむ-しゅみっと)の正規直交化法というのは、一言でいうと、基底を無理やり大きさが1で直交化するように変形する手法のことです。
「なんで直交化する必要があるの?」というと、三角化の部分でも述べた通り、固有値がすべて実数の正方行列は直交行列で三角化できるので、その直交行列を求める際に使います。
正規直交系
簡単に言うと、正規直交系というのは、直交していて、かつ大きさが\(1\)のベクトルのことを指します。
正規直交系
計量線型空間\(V\)において、\(V\)の\(m\)個のベクトル\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_m\)が、正規直交系は実は線型独立です。
定理7.
正規直交系は線型独立である。定理7.の証明
\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_m\)を正規直交系とします。
今、
$$
c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+\dots+c_m\boldsymbol{a}_m=\boldsymbol{0}
$$
とすると、任意の\(i\ (1\leq i\leq m)\)に対して、\(\left(\boldsymbol{a}_i,\boldsymbol{0}\right)=0\)であるから、
\begin{eqnarray}
0&=&\left(\boldsymbol{a}_i,c_1\boldsymbol{a}_1+c_2\boldsymbol{a}_2+\dots+c_m\boldsymbol{a}_m\right)\\
&=&\sum_{j=1}^mc_j\left(\boldsymbol{a}_i,\boldsymbol{a}_j\right)\\
&=&c_i\left(\boldsymbol{a}_i,\boldsymbol{a}_i\right)=c_i
\end{eqnarray}
です。
よって、\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_m\)線型独立です。
定理7.の証明終わり
正規直交基底
これは簡単です。
正規直交系で、かつ基底のときに正規直交基底といいます。
正規直交基底
正規直交系である基底のことを正規直交基底という。正規直交基底はまさしく座標系そのものになります。
これは以前話した通りです(詳しくは【線型代数学の基礎シリーズ】線型空間編 その2を御覧ください)。
正規直交基底の最たる例は
$$
\boldsymbol{e}_1=
\left(
\begin{array}{c}
1\\
0\\
0\\
\vdots\\
0
\end{array}
\right),\quad
\boldsymbol{e}_2=
\left(
\begin{array}{c}
0\\
1\\
0\\
\vdots\\
0
\end{array}
\right),\dots,
\boldsymbol{e}_n=
\left(
\begin{array}{c}
0\\
0\\
\vdots\\
0\\
1
\end{array}
\right)
$$
です。
確かに、どの\(\boldsymbol{e}_i\)も大きさが\(1\)で、しかもどの\(1\leq i,j\leq n\ (i\neq j)\)に対しても\(\left(\boldsymbol{e}_i,\boldsymbol{e}_j\right)=0\)です。
正規直交基底は基底なので、\(V\)の任意の要素は正規直交基底の線型結合で一意的に表現することができます。
実は、その際の係数が特徴的です。
定理8.
\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\)を計量線型空間\(V\)の正規直交基底とする。\(V\)の任意のベクトル\(\boldsymbol{x}\)は一意的に $$ \boldsymbol{x}=x_1\boldsymbol{a}_1+x_2\boldsymbol{a}_2+\dots+x_n\boldsymbol{a}_n,\quad x_i=\left(\boldsymbol{x},\boldsymbol{a}_i\right) $$ と書かれる。定理8.の証明
\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\)を計量線型空間\(V\)の正規直交基底とします。
このとき\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\)は基底なので、任意の\(V\)のベクトル\(\boldsymbol{x}\)は\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_n\)の線型結合で一意的に表現できます。
故に証明すべきことは、線型結合の係数の部分です。
しかし、これも単純です。
\begin{eqnarray}
\left(\boldsymbol{a}_i,\boldsymbol{x}\right)&=&\left( \boldsymbol{a}_i,x_1\boldsymbol{a}_1+x_2\boldsymbol{a}_2+\dots+x_n\boldsymbol{a}_n\right)\\
&=&\sum_{j=1}^nx_i\left(\boldsymbol{a}_i,\boldsymbol{a}_j\right)\\
&=&x_i
\end{eqnarray}
となるので、成り立ちます。
定理8.の証明終わり
正規直交基底は1つとは限りません。
例えば、次も正規直交基底です。
例9.
$$
\boldsymbol{a}_1=
\left(
\begin{array}{c}
\displaystyle\frac{1}{\sqrt{2}}\\
\displaystyle\frac{1}{\sqrt{2}}\\
0
\end{array}
\right),\quad
\boldsymbol{a}_2=
\left(
\begin{array}{c}
\displaystyle\frac{1}{\sqrt{2}}\\
\displaystyle-\frac{1}{\sqrt{2}}\\
0
\end{array}
\right),\quad
\boldsymbol{a}_3=
\left(
\begin{array}{c}
0\\
0\\
1
\end{array}
\right)
$$
実際、
- \(\displaystyle\|\boldsymbol{a}_1\|=\sqrt{\frac{1}{2}+\frac{1}{2}+0}=1\)、
- \(\displaystyle\|\boldsymbol{a}_2\|=\sqrt{\frac{1}{2}+\frac{1}{2}+0}=1\)、
- \(\displaystyle\|\boldsymbol{a}_3\|=\sqrt{0+0+1}=1\)
であり、
- \(\displaystyle\left(\boldsymbol{a}_1,\boldsymbol{a}_2\right)=\frac{1}{2}-\frac{1}{2}+0=0\)、
- \(\displaystyle\left(\boldsymbol{a}_2,\boldsymbol{a}_3\right)=0+0+0=0\)、
- \(\displaystyle\left(\boldsymbol{a}_1,\boldsymbol{a}_3\right)=0+0+0=0\)
です。
そして、行列
$$
\left( \boldsymbol{a}_1\ \boldsymbol{a}_2\ \boldsymbol{a}_3\right)=
\begin{pmatrix}
\displaystyle\frac{1}{\sqrt{2}}&\displaystyle\frac{1}{\sqrt{2}}&0\\
\displaystyle\frac{1}{\sqrt{2}}&\displaystyle-\frac{1}{\sqrt{2}}&0\\
0&0&1\\
\end{pmatrix}
$$
の行列式を計算すると\(-1\neq0\)となるから、基底です。
故に\(\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3\)は正規直交基底です。
グラム-シュミットの正規直交化法
では、線型独立なベクトルが与えられたとき、そのベクトルから正規直交基底を作り出す方法であるグラム-シュミットの正規直交化法を解説します。
つまり、計量線型空間\(V\)の線型独立なベクトル\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_r\)が与えられたとき、これらのベクトルから正規直交系\(\boldsymbol{v}_1,\dots,\boldsymbol{v}_r\)を作り出す方法、ということです。
まず、\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_r\)は線型独立なので、\(\boldsymbol{a}_1\neq0\)です。
従って、
$$
\boldsymbol{v}_1=\frac{1}{\|\boldsymbol{a}_1\|}\boldsymbol{a}_1
$$
とすることで、\(\|\boldsymbol{v}_1\|=1\)となります。
次に、\(\boldsymbol{a}_2\)と\(\boldsymbol{v}_1\)が直交するように\(\boldsymbol{a}_2\)を変形していきます。
ちょっとだけテクニカルです。
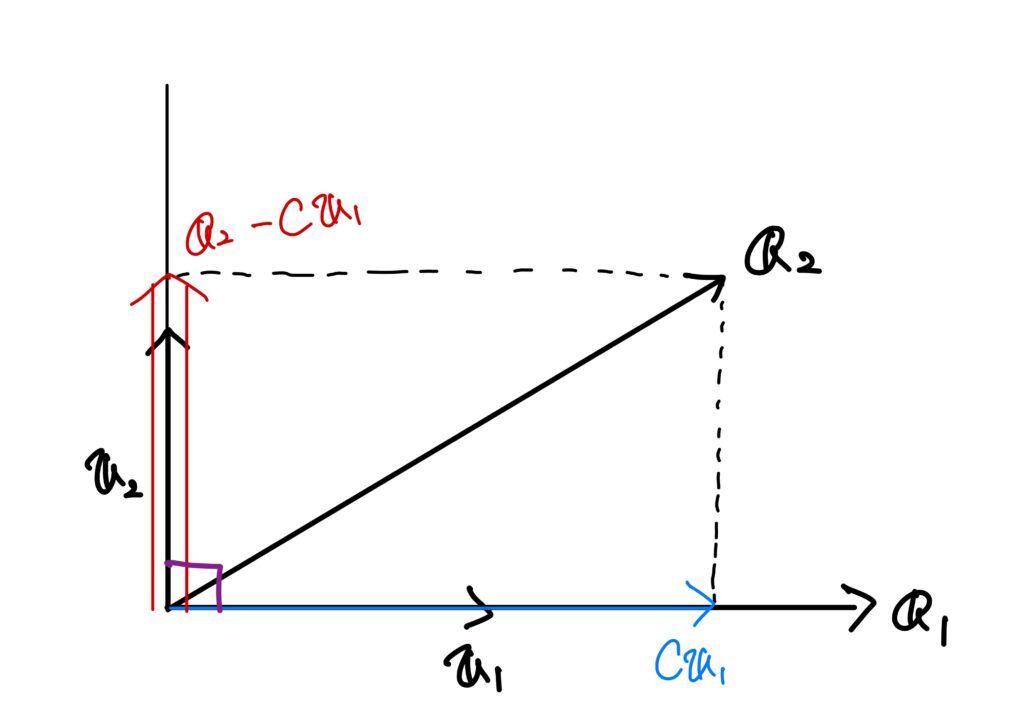
\(\boldsymbol{v}_1\)は\(\boldsymbol{a}_1\)の長さを調節しただけですので、\(\boldsymbol{v}_1\)は\(\boldsymbol{a}_1\)上にあります。
ここで、\(\boldsymbol{a}_2\)を\(\boldsymbol{v}_1\)と直行するようにしたいわけですので、\(\boldsymbol{a}_2\)を\(\boldsymbol{a}_1\)方向と、それに直交する方向に分解します。
このときに重要になるのが\(\boldsymbol{a}_2\)を分解したときの\(\boldsymbol{a}_2\)方向のベクトルです。
このベクトルは、\(\boldsymbol{a}_1\)方向なのですから、\(\boldsymbol{v}_1\)の定数倍です。
その定数を\(c\)と置きます。
ということは、\(\boldsymbol{a}_1\)と、特に\(\boldsymbol{v}_1\)と直交するベクトルは\(\boldsymbol{a}_2-c\boldsymbol{v}_1\)です。
従って、このような\(c\)を求めてしまえば、\(\boldsymbol{a}_2-c\boldsymbol{v}_1\)は\(\boldsymbol{v}_1\)と直交するわけです。
では、その\(c\)を求めてみましょう。
今求めたいのは\(\left(\boldsymbol{a}_2-c\boldsymbol{v}_1,\boldsymbol{v}_1\right)=0\)を満たす\(c\)です。
故に、
$$
\left(\boldsymbol{a}_2-c\boldsymbol{v}_1,\boldsymbol{v}_1\right)=\left(\boldsymbol{a}_2,\boldsymbol{v}_1\right)-c\left(\boldsymbol{v_1},\boldsymbol{v}_1\right)=0
$$
であることと、\(\|\boldsymbol{v}_1\|^2=\left(\boldsymbol{v}_1,\boldsymbol{v}_1\right)=1\)であることから、
$$
c=\frac{\left(\boldsymbol{a}_2,\boldsymbol{v}_1\right)}{\left(\boldsymbol{v_1},\boldsymbol{v}_1\right)}=\left(\boldsymbol{a}_2,\boldsymbol{v}_1\right)
$$
となります。
従って、\(\boldsymbol{v}_1\)に直交するベクトルは\(\boldsymbol{a}_2-c\boldsymbol{v}_1\)ということになります。
さて、直交することは分かりました。
問題は\(\boldsymbol{v}_1\)と\(\boldsymbol{a}_2-c\boldsymbol{v_1}\)が線型独立なのか?ということです。
線型独立なんです。
実際、
$$
k_1\boldsymbol{v}_1+k_2(\boldsymbol{a}_2-c\boldsymbol{v_1})=\boldsymbol{0}
$$
とすると、
$$
(k_1-ck_2)\boldsymbol{v}_1+k_2\boldsymbol{a}_2=\boldsymbol{0}
$$
となり、\(\displaystyle\boldsymbol{v}_1=\frac{1}{\|\boldsymbol{a}_1\|}\boldsymbol{a}_1\)なので、
$$
\frac{1}{\|\boldsymbol{a}_1\|}(k_1-ck_2)\boldsymbol{a}_1+k_2\boldsymbol{a}_2=\boldsymbol{0}
$$
となります。
ここで、\(\boldsymbol{a}_1,\boldsymbol{a}_2\)は線型独立なので、
$$
\frac{1}{\|\boldsymbol{a}_1\|}(k_1-ck_2)=k_2=0
$$
です。
また、\(\|\boldsymbol{a}_1\|\neq0\)なので、\(k_1=k_2=0\)となります。
従って、\(\boldsymbol{v}_1\)と\(\boldsymbol{a}_2-c\boldsymbol{v_1}\)は線型独立です。
故に、後は\(\boldsymbol{a}_2-c\boldsymbol{v_1}\)の大きさを調節すればOKです。
以上のことから、
$$
\boldsymbol{v}_2=\frac{\boldsymbol{a}_2-c\boldsymbol{v_1}}{\|\boldsymbol{a}_2-c\boldsymbol{v_1}\|}
$$
とすれば良いことが分かります。
ここで、\(\boldsymbol{a}_1\)が生成する線型空間と、\(\boldsymbol{v}_1,\boldsymbol{v_2}\)が生成する線型空間は一致しています。
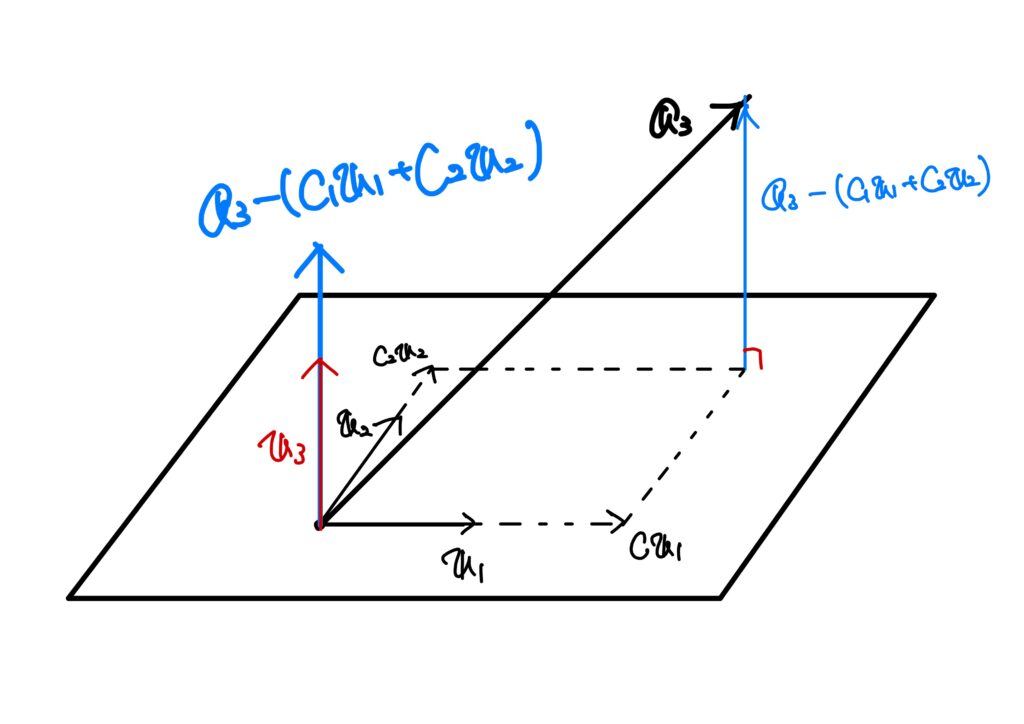
今までのプロセスを続けるわけですが、もう1ステップだけやってみます。
3番目のベクトル\(\boldsymbol{a}_3\)に対して、\(c_1=\left(\boldsymbol{a}_3,\boldsymbol{v}_1\right)\)、\(c_2=\left(\boldsymbol{a}_3,\boldsymbol{v}_2\right)\)としましょう。
このとき、
$$
\left(\boldsymbol{a}_3-(c_1\boldsymbol{v}_1+c_2\boldsymbol{v}_2),\boldsymbol{v}_i\right)\ (i=1,2)
$$
となります。
\(\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3\)は線型独立であり、\(\boldsymbol{v}_1,\boldsymbol{v}_2\)は\(\boldsymbol{a}_1,\boldsymbol{a}_2\)の線型結合で表されるので、
$$
\boldsymbol{a}_3-(c_1\boldsymbol{v}_1+c_2\boldsymbol{v}_2)\neq\boldsymbol{0}
$$
です。
従って、
$$
\boldsymbol{v}_3=\frac{\boldsymbol{a}_3-(c_1\boldsymbol{v}_1+c_2\boldsymbol{v}_2)}{\|\boldsymbol{a}_3-(c_1\boldsymbol{v}_1+c_2\boldsymbol{v}_2)\|}
$$
とすれば、
$$
\left(\boldsymbol{v}_3,\boldsymbol{v}_i\right)=0\ (i=1,2),\quad \|\boldsymbol{v}_3\|=1
$$
となります。
この操作を続ければOKです。
厳密には、帰納法で構成します。
\(1\leq k<r\)なる\(k\)に対して、正規直交系\(\boldsymbol{v}_1,\dots,\boldsymbol{v}_k\)が存在して、\(1\leq \leq k\)なる任意の\(i\)に対して、\(\boldsymbol{v}_1,\dots,\boldsymbol{v}_i\)が生成する線型空間と、\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_i\)が生成する線型空間が一致しているとします。
すなわち、
$$
S[\boldsymbol{v}_1,\dots,\boldsymbol{v}_i]=S[\boldsymbol{a}_1,\dots,\boldsymbol{a}_i]\quad (i=1,2,\dots,k)
$$
だとします。
このとき、
$$
c_i=\left(\boldsymbol{a}_{k+1},\boldsymbol{v}_i\right)\quad (i=1,\dots,k)
$$
とすると、
$$
\left(\boldsymbol{a}_{k+1}-\sum_{i=1}^kc_i\boldsymbol{v}_i,\boldsymbol{v}_j\right)=0\quad (j=1,\dots,k)
$$
です。
仮定から、\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_k,\boldsymbol{a}_{k+1}\)が線型独立で、帰納法の仮定から\(\boldsymbol{v}_1,\dots,\boldsymbol{v}_k\)は\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_k\)の線型結合で表されるから、
$$
\boldsymbol{a}_{k+1}-\sum_{i=1}^kc_i\boldsymbol{v}_i\neq\boldsymbol{0}
$$
です。
従って、
$$
\boldsymbol{v}_{k+1}=\frac{\boldsymbol{a}_{k+1}-\sum_{i=1}^kc_i\boldsymbol{v}_i}{\|\boldsymbol{a}_{k+1}-\sum_{i=1}^kc_i\boldsymbol{v}_i\|}
$$
とすると、
$$
\left(\boldsymbol{v}_{k+1},\boldsymbol{v}_j\right)=0\quad(j=1,\dots,k),\quad,\|\boldsymbol{v}_{k+1}\|=1
$$
となります。
帰納法の仮定と\(\boldsymbol{v}_{k+1}\)の式から\(\boldsymbol{v}_{k+1}\)は\(\boldsymbol{a}_1,\dots,\boldsymbol{a}_{k+1}\)の線型結合で表され、同じ式から\(\boldsymbol{k+1}\)は\(\boldsymbol{v}_1,\dots,\boldsymbol{v}_{k+1}\)の線型結合で表されるから、
$$
S[\boldsymbol{v}_1,\dots,\boldsymbol{v}_{k+1}]=S[\boldsymbol{a}_1,\dots,\boldsymbol{a}_{k+1}]
$$
が成り立ちます。
このようにして、帰納法による構成が完了です。
いっちょ計算してみっか。
してみましょう。
例10.グラム-シュミットの正規直交化法を用いて次のベクトルを正規直交化します。
$$
\boldsymbol{a}_1=
\left(
\begin{array}{c}
1\\
0\\
1
\end{array}
\right),\quad
\boldsymbol{a}_2=
\left(
\begin{array}{c}
-1\\
1\\
3
\end{array}
\right),\quad
\boldsymbol{a}_3=
\left(
\begin{array}{c}
1\\
-1\\
2
\end{array}
\right)
$$
順々に計算してみます。
①\(\boldsymbol{v}_1\)を求める。
$$
\boldsymbol{v}_1=\frac{1}{\|\boldsymbol{a}_1\|}\boldsymbol{a}_1=\frac{1}{\sqrt{2}}
\left(
\begin{array}{c}
1\\
0\\
1
\end{array}
\right)
$$
②\(\boldsymbol{v}_2\)を求める。
$$
\boldsymbol{a}_2^\prime=\boldsymbol{a}_2-\left(\boldsymbol{a}_2,\boldsymbol{v}_1\right)\boldsymbol{v}_1=
\left(
\begin{array}{c}
-1\\
1\\
3
\end{array}
\right)-\sqrt{2}\cdot\frac{1}{\sqrt{2}}
\left(
\begin{array}{c}
1\\
0\\
1
\end{array}
\right)=
\left(
\begin{array}{c}
-2\\
1\\
2
\end{array}
\right)
$$
従って、
$$
\boldsymbol{v}_2=\frac{\boldsymbol{a}_2^\prime}{\|\boldsymbol{a}_2^\prime\|}=\frac{1}{3}
\left(
\begin{array}{c}
-2\\
1\\
2
\end{array}
\right)
$$
③\(\boldsymbol{v}_3\)を求める。
\begin{eqnarray}
\boldsymbol{a}_3^\prime&=&\boldsymbol{a}_3-\left(\boldsymbol{a}_3,\boldsymbol{v}_1\right)\boldsymbol{v}_1-\left(\boldsymbol{a}_3,\boldsymbol{v}_2\right)\boldsymbol{v}_2\\
&=&\left(
\begin{array}{c}
1\\
-1\\
2
\end{array}
\right)
-\frac{3}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}}
\left(
\begin{array}{c}
1\\
0\\
1
\end{array}
\right)-\frac{1}{3}\cdot\frac{1}{3}
\left(
\begin{array}{c}
-2\\
1\\
2
\end{array}
\right)\\
&=&
\frac{5}{18}
\left(
\begin{array}{c}
-1\\
-4\\
1
\end{array}
\right)
\end{eqnarray}
従って、
$$
\boldsymbol{v}_3=\frac{\sqrt{2}}{6}
\left(
\begin{array}{c}
-1\\
-4\\
1
\end{array}
\right)
$$
です。
おしまい。
グラム-シュミットの正規直交化法を使いながら、三角化してみる。
長かったッスねえ。
いよいよ、グラム-シュミットの正規直交化法を用いて実際に三角化を行ってみます。
例11. \(\displaystyle
A=
\begin{pmatrix}
1&0&0\\
0&3&2\\
0&-1&0
\end{pmatrix}
\)を直交行列で三角化してみます。
\(A\)の固有多項式\(\varphi_A(t)\)は
$$
\varphi_A(t)=
\left|
\begin{array}{c}
1-t&0&0\\
0&3-t&2\\
0&-1&-t
\end{array}
\right|
=-(t-1)^2(t-2)
$$
であるので、固有値は\(1,2\)です。
固有値\(1\)に対する固有ベクトルを求めます。
$$
\begin{pmatrix}
0&0&0\\
0&2&2\\
0&-1&-1
\end{pmatrix}
\left(
\begin{array}{c}
x\\
y\\
z
\end{array}
\right)=\boldsymbol{0}
$$
の解ですので、\(x\)な任意、\(y+z=0\)を満たす\((x,y,z)\)を成分に持つベクトルが求めたいベクトルです。
従って、
$$
\boldsymbol{x}_1=\left(
\begin{array}{c}
x\\
y\\
z
\end{array}
\right)=c_1
\left(
\begin{array}{c}
1\\
0\\
0
\end{array}
\right)+c_2
\left(
\begin{array}{c}
0\\
1\\
-1
\end{array}
\right)
$$
次に、固有値\(2\)に属する固有ベクトルを求めます。
$$
\begin{pmatrix}
-1&0&0\\
0&1&2\\
0&-1&-2
\end{pmatrix}
\left(
\begin{array}{c}
x\\
y\\
z
\end{array}
\right)=\boldsymbol{0}
$$
の解ですので、\(x=0\)、\(y+2z=0\)を満たす\((x,y,z)\)を成分に持つベクトルが求めたいベクトルです。
従って、
$$
\boldsymbol{x}_2=\left(
\begin{array}{c}
x\\
y\\
z
\end{array}
\right)=c_3
\left(
\begin{array}{c}
0\\
-2\\
1
\end{array}
\right)
$$
ここで、
$$
\boldsymbol{a}_1=\left(
\begin{array}{c}
1\\
0\\
0
\end{array}
\right),\quad
\boldsymbol{a}_2=\left(
\begin{array}{c}
0\\
1\\
-1
\end{array}
\right),\quad
\boldsymbol{a}_3=\left(
\begin{array}{c}
0\\
-2\\
1
\end{array}
\right)
$$
が直交するかを確認してみると、直交しません。
従って、グラム-シュミットの正規直交化法で正規直交化します。
①\(\boldsymbol{v}_1\)を求める。
$$
\boldsymbol{v}_1=\boldsymbol{a}_1=
\left(
\begin{array}{c}
1\\
0\\
0
\end{array}
\right)
$$
②\(\boldsymbol{v}_2\)を求める。
$$
\boldsymbol{a}_2^\prime=\boldsymbol{a}_2-\left(\boldsymbol{a}_2,\boldsymbol{v}_1\right)\boldsymbol{v}_1=
\left(
\begin{array}{c}
0\\
1\\
-1
\end{array}
\right)-0\cdot
\left(
\begin{array}{c}
1\\
0\\
0
\end{array}
\right)=
\left(
\begin{array}{c}
0\\
1\\
-1
\end{array}
\right)
$$
従って、
$$
\boldsymbol{v}_2=\frac{\boldsymbol{a}_2^\prime}{\|\boldsymbol{a}_2^\prime\|}=\frac{1}{\sqrt{2}}
\left(
\begin{array}{c}
0\\
1\\
-1
\end{array}
\right)
$$
③\(\boldsymbol{v}_3\)を求める。
\begin{eqnarray}
\boldsymbol{a}_3^\prime&=&\boldsymbol{a}_3-\left(\boldsymbol{a}_3,\boldsymbol{v}_1\right)\boldsymbol{v}_1-\left(\boldsymbol{a}_3,\boldsymbol{v}_2\right)\boldsymbol{v}_2\\
&=&\left(
\begin{array}{c}
1\\
-2\\
1
\end{array}
\right)
-0\cdot
\left(
\begin{array}{c}
1\\
0\\
0
\end{array}
\right)+\frac{3}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}}
\left(
\begin{array}{c}
0\\
1\\
-1
\end{array}
\right)\\
&=&
\left(
\begin{array}{c}
0\\
\displaystyle-\frac{1}{2}\\
\displaystyle-\frac{1}{2}
\end{array}
\right)
\end{eqnarray}
従って、
$$
\boldsymbol{v}_3=\frac{\sqrt{2}}{6}
\left(
\begin{array}{c}
0\\
\displaystyle-\frac{\sqrt{2}}{2}\\
\displaystyle-\frac{\sqrt{2}}{2}
\end{array}
\right)
$$
です。
故に、
$$
P=
\begin{pmatrix}
1&0&0\\
0&\displaystyle\frac{1}{\sqrt{2}}&-\displaystyle\frac{1}{\sqrt{2}}\\
0&-\displaystyle\frac{1}{\sqrt{2}}&-\displaystyle\frac{1}{\sqrt{2}}
\end{pmatrix}
$$
とします。
この\(P\)は直交行列です。
従って、
$$
P^{-1}=
\begin{pmatrix}
1&0&0\\
0&\displaystyle\frac{1}{\sqrt{2}}&-\displaystyle\frac{1}{\sqrt{2}}\\
0&-\displaystyle\frac{1}{\sqrt{2}}&-\displaystyle\frac{1}{\sqrt{2}}
\end{pmatrix}
$$
です。
故に
\begin{eqnarray}
P^{-1}AP&=&
\begin{pmatrix}
1&0&0\\
0&\displaystyle\frac{1}{\sqrt{2}}&-\displaystyle\frac{1}{\sqrt{2}}\\
0&-\displaystyle\frac{1}{\sqrt{2}}&-\displaystyle\frac{1}{\sqrt{2}}
\end{pmatrix}
\begin{pmatrix}
1&0&0\\
0&3&2\\
0&-1&0
\end{pmatrix}
\begin{pmatrix}
1&0&0\\
0&\displaystyle\frac{1}{\sqrt{2}}&-\displaystyle\frac{1}{\sqrt{2}}\\
0&-\displaystyle\frac{1}{\sqrt{2}}&-\displaystyle\frac{1}{\sqrt{2}}
\end{pmatrix}\\
&=&
\begin{pmatrix}
1&0&0\\
0&2\sqrt{2}&\sqrt{2}\\
0&-\sqrt{2}&-\sqrt{2}
\end{pmatrix}
\begin{pmatrix}
1&0&0\\
0&\displaystyle\frac{1}{\sqrt{2}}&-\displaystyle\frac{1}{\sqrt{2}}\\
0&-\displaystyle\frac{1}{\sqrt{2}}&-\displaystyle\frac{1}{\sqrt{2}}
\end{pmatrix}\\
&=&
\begin{pmatrix}
1&0&0\\
0&1&-3\\
0&0&2
\end{pmatrix}
\end{eqnarray}
となって、三角化完了です。
結
今回は内積、グラム-シュミットの正規直交化法について解説しました。
また、グラム-シュミットの正規直交化法を用いて実際に三角化してみました。
どんな正方行列も固有値を複素数まで許せば必ず三角化できますが、固有ベクトルは必ずしも直交しないため、直交させるためにグラム-シュミットの正規直交化法を使います。
次回は解析学に戻ります。
乞うご期待!質問、コメント等お待ちしております!






コメントをする