「行列の対角化①」【線型代数学の基礎シリーズ】固有値編その2

本記事の内容
対角化って何スか？
固有ベクトルの線型独立性
行列の固有値が相異なれば、固有ベクトルを並べた行列で対角化可能です。
固有値の重複度と固有空間の次元
1. 固有値の重複度
2. 固有値の重複度と固有空間の次元の間の関係
対角化の主定理
1. 本記事で最も言いたい定理
2. いっちょ計算してみっか。
結

本記事の内容

本記事は「行列の対角化」について解説する記事です。

本記事を読むにあたり、固有値、固有ベクトルについて知っている必要があるため、以下の記事も合わせてご覧ください。

対角化って何スか？

対角化を平たく言うと、

正方行列

$A$ に対して、

$A$ と相似な対角行列を求めること。

です。
ここで、行列の相似というのは $B=P^{-1}AP$ という正則行列 $P$ が存在するときに $A$ と $B$ は相似と言ったのでした。

これをしっかり書くと次です。

対角化、対角化可能

正方行列

$A$ が与えられたとき、

$B=P^{-1}AP$ が対角行列になるような正則行列

$P$ と

$B$ を求めることを行列

$A$ の対角化という。
そしてこのような

$P$ および

$B$ が存在するとき

$A$ は対角化可能であるという。

「ふーん。対角化ってそういうことか。」となると思いますが、一般の行列 $A$ に対して $B=P^{-1}AP$ で、かつ $B$ が対角行列となるような正則行列 $P$ が必ずしも存在するとは限りません。
では、どういうときに存在するのか、ということを本記事は固有値、固有ベクトルのコンセプトを用いて説明します。

もし仮に、正方行列 $A$ が対角行列
$D=\begin{pmatrix} \lambda_1&&\huge{O}\\ &\ddots&\\ \huge{O}&&\lambda_n \end{pmatrix}$
に相似であれば、すなわち、 $D=P^{-1}AP$ を満たすような正則行列 $P$ が存在すれば、 $\lambda_1,\dots,\lambda_n$ が $A$ の固有値全体と一致します。
実際、次の２つが成り立ったからでした。

定理1.

$n$ 次正方行列

$A$ が三角行列である時、

$A$ の固有値全体は重複も込めて

$A$ の対角成分と一致する。

定理2.

$n$ 次正方行列

$A$ および

$B$ が相似であれば、

$\varphi_A(t)=\varphi_B(t)$ である。従って、

$A$ と

$B$ の固有値全体は重複を込めて一致する。

要するに、とある条件下では固有値を対角成分に持つ対角行列に対角化できる、ということで、あるしゅ固有値の計算をするだけで対角化したあとの行列が分かってしまう、ということです。

固有ベクトルの線型独立性

まずは相異なる固有値に属する固有ベクトルは線型独立であることを示します。
これ、重要です。

相異なる固有値に属する固有ベクトルは線型独立なベクトルです。

定理3.

$n$ 次正方行列

$A$ の相異なる固有値を

$\lambda_1,\dots,\lambda_s\ (s\leq n)$ とする。各固有値

$\lambda_i$ に属する固有ベクトルを

$\boldsymbol{x}_i$ とするとき、

$\boldsymbol{x}_1,\dots,\boldsymbol{x}_s$ は線型独立である。

定理3.の証明

数学的帰納法で証明します。
$\boldsymbol{x}_1$ は固有ベクトルなので、 $\boldsymbol{x}_1\neq\boldsymbol{0}$ です。
従って、 $c_1\boldsymbol{x}_1=\boldsymbol{0}$ とするとき、 $c_1=0$ でなければなりません。
故に、 $\boldsymbol{x}_1$ は線型独立です。

次に、 $r<s$ を満たすような $r\in\mathbb{N}$ が存在して、 $\boldsymbol{x_1},\dots,\boldsymbol{x}_r$ は線型独立だとして、 $\boldsymbol{x_1},\dots,\boldsymbol{x}_r,\boldsymbol{x}_{r+1}$ も線型独立であることを示します。
そこで、背理法を用います。
すなわち、 $\boldsymbol{x_1},\dots,\boldsymbol{x}_r$ は線型独立だけれど、 $\boldsymbol{x_1},\dots,\boldsymbol{x}_r,\boldsymbol{x}_{r+1}$ は線型独立でない、すなわち線型従属だとして矛盾を導きます。

ここで、次の定理を使います。

定理4.

$V$ を線型空間とする。

$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r$ が線型独立で、

$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r,\boldsymbol{a}$ が線型従属であれば、

$\boldsymbol{a}$ は

$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_r$ の線型結合として一意的に表される。

定理4.の証明は【線型代数学の基礎シリーズ】線型空間編その2を御覧ください。

定理4.から、
$\boldsymbol{x}_{r+1}=c_1\boldsymbol{x}_1+\dots+c_r\boldsymbol{x}_r\cdots①$
と一意的に表すことができます。
$\boldsymbol{x}_{r+1}$ は固有値 $\lambda_{r+1}$ に属する固有ベクトルなので $\boldsymbol{x}_{r+1}\neq\boldsymbol{0}$ です。
従って、 $c_1,\dots,c_r$ の中に少なくとも1つは $0$ でないものが存在します。

さて、各 $\boldsymbol{x}_i$ を列ベクトルで表し、①の両辺に左から $A$ をかければ、
$A\boldsymbol{x}_{r+1}=c_1A\boldsymbol{x}_1+\dots+c_rA\boldsymbol{x}_r$
となります。
各 $\boldsymbol{x}_i$ は固有値 $\lambda_i$ に属する固有ベクトルなので、
$A\boldsymbol{x}_i=\lambda_i\boldsymbol{x}_i$
を満たすから
$\lambda_{r+1}\boldsymbol{x}_{r+1}=c_1\lambda_1\boldsymbol{x}_1+\dots+c_r\lambda_r\boldsymbol{x}_r\cdots②$
となります。
また、①の両辺に $\lambda_{r+1}$ をかけて
$\lambda_{r+1}\boldsymbol{x}_{r+1}=c_1\lambda_{r+1}\boldsymbol{x}_1+\dots+c_r\lambda_{r+1}\boldsymbol{x}_r\cdots③$
となります。
②および③により、
$c_1(\lambda_1-\lambda_{r+1})\boldsymbol{x}_1+\dots+c_r(\lambda_r-\lambda_{r+1})\boldsymbol{x}_r=\boldsymbol{0}$
ここで、仮定から固有値は相異なるので、 $1\leq i\leq r$ を満たす $i\in\mathbb{N}$ に対して $\lambda_i-\lambda_{r+1}\neq0$ であり、ある $j$ で $c_j\neq0$ なわけですので、上記の式は自明でない線型関係式です。
しかしながら、これは $\boldsymbol{x_1},\dots,\boldsymbol{x}_r$ が線型独立であることに反します。
従って、 $\boldsymbol{x_1},\dots,\boldsymbol{x}_r,\boldsymbol{x}_{r+1}$ も線型独立です。
以上のことから、相異なる固有値に属する固有ベクトル同士は線型独立です。

定理3.の証明終わり

固有値が存在する行列には対角化っぽいことができます。

次に対角化っぽい事実を示します。

定理5.

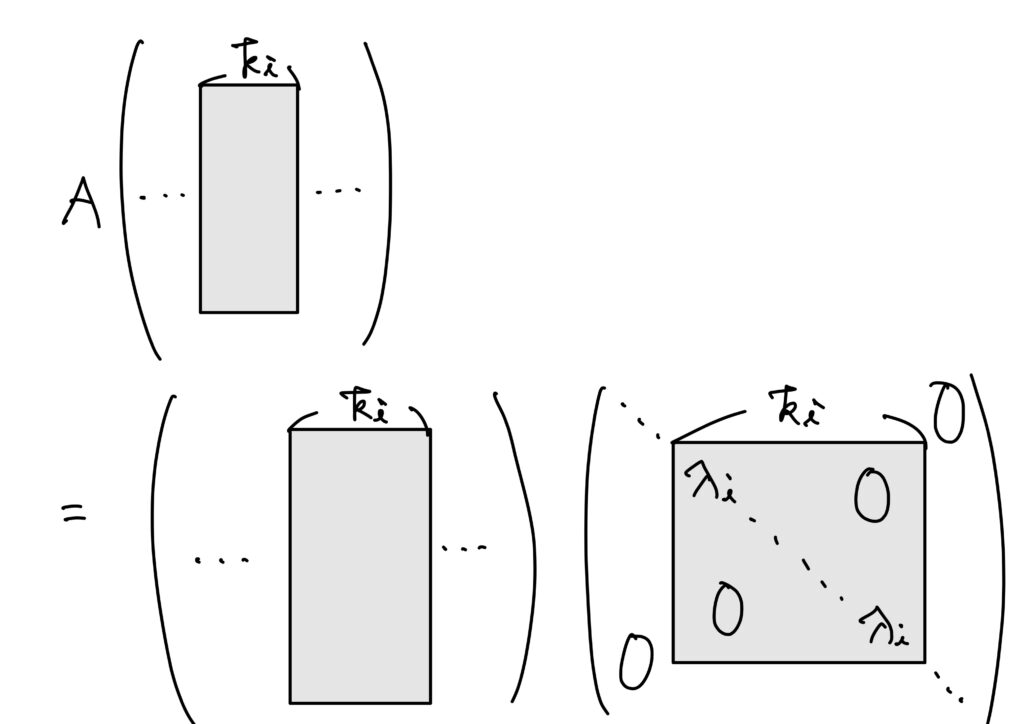
$A$ を

$n$ 次正方行列、

$\lambda_1,\dots,\lambda_n$ を

$A$ の固有値、

$\boldsymbol{x}_1,\dots,\boldsymbol{x}_n$ をそれぞれに属する固有ベクトルとする。ただし、

$\lambda_i$ は相異なるとは仮定しない。そして、

$\boldsymbol{x}_i$ を第

$i$ 列とする正方行列を

$Q$ とする。すなわち、

$Q=(\boldsymbol{x}_1\ \cdots\ \boldsymbol{x}_r)$ とする。このととき、

$AQ=Q \begin{pmatrix} \lambda_1&&\huge{O}\\ &\ddots&\\ \huge{O}&&\lambda_n \end{pmatrix}$ が成り立つ。
　逆に、

$n$ 次正方行列

$Q$ と

$\nu_i\ (i=1,\dots,n)$ が存在して、

$AQ=Q \begin{pmatrix} \nu_1&&\huge{O}\\ &\ddots&\\ \huge{O}&&\nu_n \end{pmatrix}$ を満たし、

$Q$ の各列ベクトルが零ベクトルでないならば、

$\nu_i$ は

$A$ の固有値で、

$Q$ の第

$i$ 列は固有値

$\nu_i$ に属する固有ベクトルである。

定理5.の証明

$A$ を $n$ 次正方行列、 $\lambda_1,\dots,\lambda_n$ を $A$ の固有値、 $\boldsymbol{x}_1,\dots,\boldsymbol{x}_n$ とします。

(前半の証明)

$\lambda_1,\dots,\lambda_n$ は $A$ の固有値で、 $\boldsymbol{x}_1,\dots,\boldsymbol{x}_n$ は各固有値 $\lambda_i$ に属する固有ベクトルなので
$A\boldsymbol{x}_i=\lambda_i\boldsymbol{x}_i\quad (\boldsymbol{x}_i\neq\boldsymbol{0})$
です。
すると、この両辺は列ベクトルの形をしています。
この列ベクトルを第 $i$ 列とする行列をそれぞれ考えて、次の等式を得ます。
$\begin{eqnarray} A(\boldsymbol{x}_1\ \boldsymbol{x}_2\ \dots\ \boldsymbol{x}_n)&=& (A\boldsymbol{x}_1\ A\boldsymbol{x}_2\ \dots\ A\boldsymbol{x}_n)\\ &=&(\lambda_1\boldsymbol{x}_1\ \lambda_2\boldsymbol{x}_2\ \dots\ \lambda_n\boldsymbol{x}_n)\\ &=& (\boldsymbol{x}_1\ \boldsymbol{x}_2\ \dots\ \boldsymbol{x}_n) \begin{pmatrix} \lambda1&&& \\ &\lambda_2&&\huge{O}\\ \huge{O}&&\ddots&\\ &&&\lambda_n \end{pmatrix} \end{eqnarray}$

従って、等式
$A(\boldsymbol{x}_1\ \boldsymbol{x}_2\ \dots\ \boldsymbol{x}_n)= (\boldsymbol{x}_1\ \boldsymbol{x}_2\ \dots\ \boldsymbol{x}_n) \begin{pmatrix} \lambda1&&& \\ &\lambda_2&&\huge{O}\\ \huge{O}&&\ddots&\\ &&&\lambda_n \end{pmatrix}$
ここで、 $Q=(\boldsymbol{x}_1\ \boldsymbol{x}_2\ \dots\ \boldsymbol{x}_n)$ なのだから、この式は
$AQ= Q \begin{pmatrix} \lambda1&&& \\ &\lambda_2&&\huge{O}\\ \huge{O}&&\ddots&\\ &&&\lambda_n \end{pmatrix}$
と書き直すことができます。

(後半の証明)

逆に、各列ベクトルが零ベクトルでないような $n$ 次正方行列 $Q$ と $\nu_i\ (i=1,\dots,n)$ で、
$AQ= Q \begin{pmatrix} \nu1&&& \\ &\lambda_2&&\huge{O}\\ \huge{O}&&\ddots&\\ &&&\nu_n \end{pmatrix}$
を満たしているとします。
行列 $Q$ の第 $i$ 列を $\boldsymbol{x}_i$ と書くことにすると、上の等式の両辺の第 $i$ 列を取り出して考えることで、
$A\boldsymbol{x}_i=\nu_i\boldsymbol{x}_i$
となります。
今、仮定から $\boldsymbol{x}_i\neq\boldsymbol{0}$ ですので、 $\nu_i$ は $A$ の固有値で、かつ $\boldsymbol{x}_i$ は固有値 $\nu_i$ に属する固有ベクトルです。

定理5.の証明終わり

この章で言いたかったこと

定理5.から「あれ？もうこれで対角化の話はおしまいじゃない？」と思うかもしれませんがそうではありません。
注意して置かなければならないのは、「必ずしも $Q$ は正則ではない」ということです。
というのも、 $\lambda_1,\dots,\lambda_n$ は相異なるとは仮定していないので、固有ベクトル $\boldsymbol{x}_1,\dots,\boldsymbol{x}_n$ は線型独立とは限らないからです。
言ってしまえば、固有ベクトルの中には同じベクトルがあるかもしれません。
故に、行列 $Q$ は必ずしも正則ではありません。

もし仮に $Q$ が正則であれば、 $Q$ の逆行列 $Q^{-1}$ が存在しますので、
$AQ= Q \begin{pmatrix} \lambda1&&& \\ &\lambda_2&&\huge{O}\\ \huge{O}&&\ddots&\\ &&&\lambda_n \end{pmatrix}\Leftrightarrow Q^{-1}AQ= \begin{pmatrix} \lambda1&&& \\ &\lambda_2&&\huge{O}\\ \huge{O}&&\ddots&\\ &&&\lambda_n \end{pmatrix}$
となって対角化可能です。

とどのつまり、固有値が存在するような行列に対しては、対角化”っぽい”ことができる、というわけです。
ここで「ほーん。したらば $Q$ が正則だったらい良いわけね？でもそんなん見つけられんの？」となると思います。
見つけられます。
そこで鍵となるのが固有ベクトルなのです。
少々ネタバラシですが、固有値が相異なっていれば、固有ベクトルを用いることで正則な $Q$ を見つけることができます。

行列の固有値が相異なれば、固有ベクトルを並べた行列で対角化可能です。

なんとびっくり、固有値が相異なれば固有ベクトルを並べた行列で対角化可能なのです。
先程「 $Q$ が正則だったらいいよねえ」という話をしましたが、固有値が相異なれば、固有ベクトルは線型独立ですので正則な行列となります(これは以前に証明したことで、この章の主張を証明するときに改めて明示します)。
従って、固有値が相異なるときに固有ベクトルを並べた行列は正則な行列です。
故にこの章で言いたかったことで述べた操作で対角化可能なのです。

この主張を明示します。

定理6.

$n$ 次正方行列

$A$ が相異なる

$n$ 個の固有値

$\lambda_1,\dots,\lambda_n$ をもつならば、

$A$ はこれらを対角成分に持つ対角行列に対角化可能である。つまり、ある正則行列

$P$ が存在して

$P^{-1}AP= \begin{pmatrix} \lambda_1&&\huge{O}\\ &\ddots&\\ \huge{O}&&\lambda_n \end{pmatrix}$ となる。

定理6.の証明

先程述べたことをしっかり書くだけです。

$A$ の固有値 $\lambda_1,\dots,\lambda_n$ に属する固有ベクトルを $\boldsymbol{x}_1,\dots,\boldsymbol{x}_n$ とすると、定理3.から固有ベクトルは線型独立なので、 $\boldsymbol{x}_1,\dots,\boldsymbol{x}_n$ は線型独立です。
従って、 $\boldsymbol{x}_1,\dots,\boldsymbol{x}_n$ は $\mathbb{R}^n$ の基底です。
そこで、 $\boldsymbol{x}_i$ を第 $i$ 列とするような正方行列を $P$ とします。
すなわち、 $P=\left( \boldsymbol{x}_1\ \boldsymbol{x}_2\ \dots \boldsymbol{x}_n\right)$ とします。
ここで、次の事実を使います。

定理7.

$n\in\mathbb{N}$ とし、

$A$ を

$n$ 次正方行列、

$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$ を

$A$ の行ベクトル、

$\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime,\dots,\boldsymbol{a}_n^\prime$ を

$A$ の列ベクトル、とするとき、次の条件は同値である。

$\det(A)\neq 0$
$\boldsymbol{a}_1^\prime,\boldsymbol{a}_2^\prime,\dots,\boldsymbol{a}_n^\prime$ は線型独立である。
$\boldsymbol{a}_1,\boldsymbol{a}_2,\dots,\boldsymbol{a}_n$ は線型独立である。

定理7.の証明は【線型代数学の基礎シリーズ】線型空間編その3を御覧ください。

定理7.により、 $P$ は正則行列です。
そして、定理5.から
$AP= P \begin{pmatrix} \lambda_1&&& \\ &\lambda_2&&\huge{O}\\ \huge{O}&&\ddots&\\ &&&\lambda_n \end{pmatrix}\Leftrightarrow Q^{-1}AQ= \begin{pmatrix} \lambda1&&& \\ &\lambda_2&&\huge{O}\\ \huge{O}&&\ddots&\\ &&&\lambda_n \end{pmatrix}$
が成り立ちます。
ここで、 $P$ は正則な行列なので $P$ の逆行列 $P^{-1}$ が存在します。
故に、この等式の両辺に左から $P^{-1}$ をかけて
$P^{-1}AP= \begin{pmatrix} \lambda_1&&& \\ &\lambda_2&&\huge{O}\\ \huge{O}&&\ddots&\\ &&&\lambda_n \end{pmatrix}\Leftrightarrow Q^{-1}AQ= \begin{pmatrix} \lambda1&&& \\ &\lambda_2&&\huge{O}\\ \huge{O}&&\ddots&\\ &&&\lambda_n \end{pmatrix}$
が得られます。

定理6.の証明終わり

固有値の重複度と固有空間の次元

ちょっと話は変わりますが、対角化の話を先にすすめるために少々準備をします。

固有値の重複度

固有値は必ずしも相異なるわけではありませんでした。
そこで、どのくらい重複しているか、ということを表す指標が固有値の重複度です。
一言で言ってしまえば、

行列

$A$ の固有方程式

$\varphi_A(t)=0$ の解の重複度のこと。

「は？重複度を知りたいってのに、重複度を使ってんじゃねえよ。説明になってねえよ。」という感じですね。
ちゃんと書きます。

固有値の重複度

$n$ 次正方行列

$A$ の固有値を

$\lambda_1,\dots,\lambda_d$ とする。このとき

$\lambda_i$ は相異なっていて、

$A$ の固有多項式

$\varphi_A(t)$ が

$\varphi_A(t)=(t-\lambda_1)^{r_1}\cdots(t-\lambda_d)^{r_d}$ という形をしていれば、

$r_i$ を固有値

$\lambda_i$ の重複度という。

つまり、固有多項式の各 $\lambda_i$ の累乗が重複度ということです。

固有値の重複度と固有空間の次元の間の関係

定理8.

$A$ を

$n$ 次正方行列、

$\lambda$ を

$A$ の１つの固有値とするとき、

$\lambda$ に属する固有空間の次元

$\leq\lambda$ の重複度

が成り立つ。

定理8.の証明

$r=(\lambda$ に属する固有空間 $V(\lambda)$ の次元)、 $k=(\lambda$ の重複度)としましょう。
このとき、 $\boldsymbol{x}_1,\dots,\boldsymbol{x}_r$ を連立斉一次方程式
$\left( A-\lambda I_n\right)\boldsymbol{x}=\boldsymbol{0}$
１組の解とします。
これに $n-r$ 個のベクトル $\boldsymbol{x}_{r+1},\dots,\boldsymbol{x}_n$ を補充して、
$\boldsymbol{x}_1,\dots,\boldsymbol{x}_r,\boldsymbol{x}_{r+1},\dots,\boldsymbol{x}_n$
が $\mathbb{R}^n$ の基底となるようにすることができます。

実際、次が成り立つからです。

補題9.

$V$ を

$n$ 次元線型空間とする。

$V$ のベクトルの組

$\boldsymbol{a}_1,\dots,\boldsymbol{a}_r$ が線型独立で、

$r<n$ であれば、

$n-r$ 個のベクトル

$\boldsymbol{a}_{r+1},\dots,\boldsymbol{a}_n$ を選んで

$\boldsymbol{a}_1,\dots,\boldsymbol{a}_r,\boldsymbol{a}_{r+1},\dots,\boldsymbol{a}_n$ が

$V$ の基底となるようにできる。

補題9.の証明

$\boldsymbol{b}_1,\dots,\boldsymbol{b}_n$ を $V$ の基底とします。
$r+n$ このベクトル $\boldsymbol{a}_1,\dots,\boldsymbol{a}_r,\boldsymbol{b}_1,\dots,\boldsymbol{b}_n$ の中から、この順番に線型独立なものを選びます。
すなわち、次の操作をします。

まず、 $\boldsymbol{a}_1,\dots,\boldsymbol{a}_r,\boldsymbol{b}_1$ が線型独立ならば、 $\boldsymbol{b}_1$ を付け加えて、線型従属ならば $\boldsymbol{b}_1$ を除きます。
この操作を $\boldsymbol{b}_1,\dots,\boldsymbol{b}_n$ に順番に行った結果を
$\boldsymbol{a}_1,\dots,\boldsymbol{a}_r,\boldsymbol{b}_{i_1},\dots,\boldsymbol{b}_{i_s}$
としましょう。
このベクトルの組は線型独立であり、この里の任意の $\boldsymbol{b}_j$ を付け加えると線型従属になってしまいます。
ここで、定理4.から $\boldsymbol{b}_j$ はこれらの線型結合で表されます。
従って、この組は線型空間 $V$ の基底です。
勿論 $r+s=n$ です。
この $\boldsymbol{b}_{i_1},\dots,\boldsymbol{b}_{i_s}$ を順々に $\boldsymbol{a}_{r+1},\dots,\boldsymbol{a}_n$ とすればOKです。

補題9.の証明終わり

さて、定理8.の証明に戻ります。

今、補題9.により
$\boldsymbol{x}_1,\dots,\boldsymbol{x}_r,\boldsymbol{x}_{r+1},\dots,\boldsymbol{x}_n$
が $\mathbb{R}^n$ の基底となるようにすることができます。

そこで、 $n$ 次正方行列 $P$ を
$P=\left( \boldsymbol{x}_1\ \cdots\ \boldsymbol{x}_r\ \boldsymbol{x}_{r+1}\ \cdots\ \boldsymbol{x}_n\right)$
によって定めると、定理7.から $P$ は正則で、
$\begin{eqnarray} AP&=&A\left( \boldsymbol{x}_1\ \cdots\ \boldsymbol{x}_r\ \boldsymbol{x}_{r+1}\ \cdots\ \boldsymbol{x}_n\right)\\ &=&\left( A\boldsymbol{x}_1\ \cdots\ A\boldsymbol{x}_r\ A\boldsymbol{x}_{r+1}\ \cdots\ A\boldsymbol{x}_n\right)\\ &=& \left( \lambda_1\boldsymbol{x}_1\ \cdots\ \lambda_r\boldsymbol{x}_r\ A\boldsymbol{x}_{r+1}\ \cdots\ A\boldsymbol{x}_n\right)\\ \end{eqnarray}$
です。
ただし、最後の式は $\boldsymbol{x}_1,\dots,\boldsymbol{x}_r$ が
$\left( A-\lambda I_n\right)\boldsymbol{x}_i=\boldsymbol{0}$
を満たしていたからです。

ここで、 $A\boldsymbol{x}_{r+1},\cdots,A\boldsymbol{x}_n$ は $P$ の列ベクトルの線型結合で書けるから、
$\begin{eqnarray} AP&=& \left( \lambda_1\boldsymbol{x}_1\ \cdots\ \lambda_r\boldsymbol{x}_r\ A\boldsymbol{x}_{r+1}\ \cdots\ A\boldsymbol{x}_n\right)\\ &=&\left( \boldsymbol{x}_1\ \cdots\ \boldsymbol{x}_r\ \boldsymbol{x}_{r+1}\ \cdots\ \boldsymbol{x}_n\right) \left( \begin{array}{ccc|ccc} \lambda&&O&&&\\ &\ddots&&&B&\\ O&&\lambda&&&\\ \hline &&&&&\\ &O&&&C&\\ &&&&&\\ \end{array}\right)\\ &=& P\left( \begin{array}{ccc|ccc} \lambda&&O&&&\\ &\ddots&&&B&\\ O&&\lambda&&&\\ \hline &&&&&\\ &O&&&C&\\ &&&&&\\ \end{array}\right) \end{eqnarray}$
と表されます。
ただし、左上の対角行列は $(r,r)$ 型です。

従って、
$P^{-1}AP= \left( \begin{array}{ccc|ccc} \lambda&&O&&&\\ &\ddots&&&B&\\ O&&\lambda&&&\\ \hline &&&&&\\ &O&&&C&\\ &&&&&\\ \end{array}\right)$
です。

ここで、次の事実を使います。

定理10.

$n$ 次正方行列

$A$ が

$A=\begin{pmatrix} B&C\\ O&D\\ \end{pmatrix}$ の形をしているとする。ここで

$B$ は

$r$ 次正方行列、

$C$ は

$(r,s)$ 型の行列、

$D$ は

$s$ 次正方行列、

$O$ は

$(s,r)$ 型の零行列とする。このとき、

$\varphi_A(t)=\varphi_B(t)\cdot\varphi_D(t)$ が成り立つ。従って、行列

$A$ の固有値の全体は、重複も込めて行列

$B$ の固有値と行列

$D$ の固有値をあわせたものと一致する。

定理10.の証明は【線型代数学の基礎シリーズ】固有値編その1を御覧ください。

定理10.を使うことで、 $P^{-1}AP$ の固有多項式 $\varphi_{P^{-1}AP}(t)$ は
$\varphi_{P^{-1}AP}(t)=(\lambda-t)^r\cdot\det\left( C-tI_{n-r}\right)$
です(ただし、 $I_{n-r}$ は $n-r$ 次の単位行列です)。

更に、次の事実を使います。

定理11.

$n$ 次正方行列

$A$ および

$B$ が相似であれば、

$\varphi_A(t)=\varphi_B(t)$ である。従って、

$A$ と

$B$ の固有値全体は重複を込めて一致する。

定理11.の証明は【線型代数学の基礎シリーズ】固有多項式編その1を御覧ください。

定理11.により、 $P^{-1}AP$ と $A$ の固有値は等しいので、
$\varphi_A(t)=\varphi_{P^{-1}AP}(t)=(\lambda-t)^r\cdot\det\left( C-tI_{n-r}\right)$
です。
$\lambda$ は $\varphi_A(t)$ の $k$ 重解でしたから、 $r\leq k$ ということが成り立ちます。

定理8.の証明終わり

対角化の主定理

本記事で最も言いたい定理

本記事で最も言いたいことです。

定理12.

$n$ 次正方行列

$A$ について次の4条件は同値である。

$A$ は対角化可能である。
$A$ の固有多項式は重複を込めて $n$ 個の解を持ち、かつ各固有値の重複度はその固有値に属する固有空間の次元に一致する。

$A$

$\lambda_1,\dots,\lambda_s$

$\lambda_i$

$k_i$

$\lambda_i$

$V(\lambda_i)$

$\sum_{i=1}^sk_i=n,\quad k_i=\dim(V(\lambda_i))\ (i=1,\dots,s)$

$A$ の各固有値に属する固有空間の次元の和は $n$ になる。

$A$

$\lambda_1,\dots,\lambda_s$

$\lambda_i$

$V(\lambda_i)$

$\sum_{i=1}^s\dim\left( V(\lambda_i)\right)=n$

$n$ 個の線型独立な $A$ の固有ベクトルが存在する。

定理12.の証明

(1. $\Rightarrow$ 2.の証明)

$A$ は対角化可能なので、正則行列 $P$ が存在して、
$P^{-1}AP= \begin{pmatrix} \alpha_1&&\huge{O} \\ &\ddots&\\ \huge{O}&&\alpha_n \end{pmatrix}$
とできます。
$\alpha_i$ は $P^{-1}AP$ の固有値ですので、定理11.から $A$ の固有値でもあります。
従って、順番を変えてまとめれば、 $\lambda_1$ のブロック、 $\lambda_2$ のブロック、 $\cdots$ 、 $\lambda_s$ のブロックと言う具合にできます。
順番を変えるというのは $P$ の取替でできますので、結局の所 $P$ が存在して、
$P^{-1}AP= \left( \begin{array}{c} \lambda_1&&&&&&&\\ &\ddots&&&&&&\\ &&\lambda_1&&&\huge{O}&&\\ &&&\ddots&&&&\\ &&&&\ddots&&&\\ &&\huge{O}&&&\lambda_s&&\\ &&&&&&\ddots&\\ &&&&&&&\lambda_s\\ \end{array} \right)$
とできます。
ただし、左上から対角に $\lambda_1$ が $k_1$ 個、 $\cdots$ 、 $\lambda_s$ が $k_s$ 個並んでいます。
ここで、 $k_i$ は固有値 $\lambda_i$ の重複度であり、かつ $\displaystyle\sum_{i=1}^sk_i=n$ を満たしています。
この氷裂の等式の両辺に左から $P$ をかけることで、
$AP=P \left( \begin{array}{c} \lambda_1&&&&&&&\\ &\ddots&&&&&&\\ &&\lambda_1&&&\huge{O}&&\\ &&&\ddots&&&&\\ &&&&\ddots&&&\\ &&\huge{O}&&&\lambda_s&&\\ &&&&&&\ddots&\\ &&&&&&&\lambda_s\\ \end{array} \right)$
となります。

ここで、行列 $P$ を列ベクトルが並んだものとみなし、上の行列の積の等式から、両辺の第 $i$ どうしの等式を抜き出すことによって、 $P$ の

最初の $k_1$ 個の列ベクトルは固有値 $\lambda_1$ に属する固有ベクトル、
次の $k_2$ 個の列ベクトルは固有値 $\lambda_2$ に属する固有ベクトル、
$\vdots$
最後の $k_s$ 個の列ベクトルは固有値 $\lambda_s$ に属する固有ベクトル

であることが分かります。

仮定から $P$ は正則な行列なので、 $P$ の列ベクトル全体は線型独立です。
従って、特に $i$ 番目のブロックに対応する $P$ の $k_i$ 個の列ベクトルの集合も線型独立であり、これらのベクトルは固有値 $\lambda_i$ に属する固有ベクトルです。

従って、
$k\leq\dim\left( V(\lambda_i)\right)\quad (i=1,\dots,s)$
が成り立ちます。
定理8.から、
$k\geq\dim\left( V(\lambda_i)\right)\quad (i=1,\dots,s)$
ですので、
$k=\dim\left( V(\lambda_i)\right)\quad (i=1,\dots,s)$
が成り立ちます。

(2. $\Rightarrow$ 3.の証明)

$\displaystyle k_i=\dim\left( V(\lambda_i)\right)$ を $\displaystyle \sum_{i=1}^sk_i=n$ に代入することで、
$\sum_{i=1}^s\dim\left( V(\lambda_i)\right)=n$
が得られます。

(3. $\Rightarrow$ 4.の証明)

$r_i=\dim\left( V(\lambda_i)\right)$ として、 $V(\lambda_i)$ の１つの基底を $\boldsymbol{w}_1^{(i)},\dots,\boldsymbol{w}_{r_i}^{(i)}$ とします。
仮定から
$\sum_{i=1}^sr_i=n$
です。
このとき、 $n$ 個のベクトル
$\boldsymbol{w}_1^{(1)},\dots,\boldsymbol{w}_{r_1}^{(1)},\dots,\boldsymbol{w}_1^{(s)},\dots,\boldsymbol{w}_{r_s}^{(s)}$
が線型独立だということを示しましょう。
故に、
$\sum_{i=1}^s\sum_{j=1}^{r_i}c_{ij}\boldsymbol{w}_{j}^{(i)}=\boldsymbol{0}$
としましょう。
ここで、
$\boldsymbol{v}^{(i)}=\sum_{j=1}^{r_i}c_{ij}\boldsymbol{w}_j^{(i)}$
とすると、
$\boldsymbol{v}^{(i)}\in V(\lambda_i),\quad \boldsymbol{v}^{(1)}+\dots+\boldsymbol{v}^{(s)}=\boldsymbol{0}$
です。
今、ベクトル $\boldsymbol{v}^{(1)},\dots,\boldsymbol{v}^{(s)}$ のうち、零ベクトルでないものがあるとすれば、それらを集めたものは定理3.から線型独立です。
これは、
$\boldsymbol{v}^{(1)}+\dots+\boldsymbol{v}^{(s)}=\boldsymbol{0}$
に矛盾します。

従って、
$\boldsymbol{v}^{(i)}=\sum_{j=1}^{r_i}c_{ij}\boldsymbol{w}_j^{(i)}=\boldsymbol{0}$
が、任意の $i=1,\dots,s$ に対して成り立ちます。
しかしながら、 $\boldsymbol{w}_1^{(i)},\dots,\boldsymbol{w}_{r_i}^{(i)}$ は線型独立だったので、 $c_{ij}=0\ (i=1,\dots,s,\ j=1,dots,r_i)$ が成り立ちます。
すなわち、
$\boldsymbol{w}_j^{(i)}\quad (i=1,\dots,s,\ j=1,dots,r_i)$
は線型独立になります。

こうして、 $n$ 個の線型独立な $A$ の固有ベクトルの存在が示されました。

(4. $\Rightarrow$ 1.の証明)

$A\boldsymbol{w}_i=\lambda_i\boldsymbol{w}_i\ (i=1,\dots,n)$ かつ $\boldsymbol{w}_1,\dots,\boldsymbol{w}_n$ が線型独立だとします。
そこで、 $\boldsymbol{w}_1,\dots,\boldsymbol{w}_n$ を列ベクトルに持つ $n$ 次正方行列を $P=(\boldsymbol{w}_1\ \dots\ \boldsymbol{w}_n)$ とすると、定理7.から $P$ は正則で、定理5.から等式
$AP= P \begin{pmatrix} \lambda1&&& \\ &\lambda_2&&\huge{O}\\ \huge{O}&&\ddots&\\ &&&\lambda_n \end{pmatrix}$
です。
従って、
$P^{-1}AP= \begin{pmatrix} \lambda1&&& \\ &\lambda_2&&\huge{O}\\ \huge{O}&&\ddots&\\ &&&\lambda_n \end{pmatrix}$
となって、 $A$ は対角化可能です。

定理12.の証明終わり

個人的によく使うのは4.です。

いっちょ計算してみっか。

例13. $\displaystyle A= \begin{pmatrix} 1&1\\ 0&2\\ \end{pmatrix}$ が対角化可能か判定して、対角化可能なら対角化しましょう。

まず、固有値を求めてみます。

$\varphi_A(t)=\det\left( A-t I_2\right)= \left| \begin{array} 1-t&1\\ 0&2-t\\ \end{array} \right| =(t-1)(t-2)$
となるので、 $\varphi_A(t)=0$ の解は $t=1,2$ となって、固有値 $\lambda=1,2$ です。
固有値が相異なっているので、 $\lambda_1=1$ に属する固有ベクトルと $\lambda_2=2$ に属する固有ベクトルは線型独立です。
従って、定理12.から $A$ は対角化可能です。

実は、すでに対角化可能だということが分かった時点で、定理5.から
$\begin{pmatrix} 1&0\\ 0&2\\ \end{pmatrix}$
と対角化できることが分かります。
しかし、一度正則行列 $P$ を求めて実際に計算してみます。
そこで、それぞれの固有値に属する固有ベクトルを求めます。

( $\lambda_1=1$ に属する固有ベクトル)

$\begin{pmatrix} 1-\lambda_1&1\\ 0&2-\lambda_1\\ \end{pmatrix} \left( \begin{array}{c} x\\ y\\ \end{array} \right)= \begin{pmatrix} 1-1&1\\ 0&2-1\\ \end{pmatrix} \left( \begin{array}{c} x\\ y\\ \end{array} \right)= \begin{pmatrix} 0&1\\ 0&1\\ \end{pmatrix} \left( \begin{array}{c} x\\ y\\ \end{array} \right)=\boldsymbol{0}$
としたとき、この解は
$c\left( \begin{array}{c} 1\\ 0\\ \end{array} \right)\quad (c\in\mathbb{R})$
です。
ここで、
$\boldsymbol{x}_1= \left( \begin{array}{c} 1\\ 0\\ \end{array} \right)$
とします。

( $\lambda_2=2$ に属する固有ベクトル)

$\begin{pmatrix} 1-\lambda_2&1\\ 0&2-\lambda_2\\ \end{pmatrix} \left( \begin{array}{c} x\\ y\\ \end{array} \right)= \begin{pmatrix} 1-2&1\\ 0&2-2\\ \end{pmatrix} \left( \begin{array}{c} x\\ y\\ \end{array} \right)= \begin{pmatrix} -1&1\\ 0&0\\ \end{pmatrix} \left( \begin{array}{c} x\\ y\\ \end{array} \right)=\boldsymbol{0}$
としたとき、この解は
$c\left( \begin{array}{c} 1\\ 1\\ \end{array} \right)\quad (c\in\mathbb{R})$
です。
ここで、
$\boldsymbol{x}_2= \left( \begin{array}{c} 1\\ 1\\ \end{array} \right)$
とします。

従って、
$P=(\boldsymbol{x}_1\ \boldsymbol{x}_2)= \begin{pmatrix} 1&1\\ 0&1\\ \end{pmatrix}$
とします。
このとき、 $\det(P)=1\neq0$ ですので、 $P$ は正則です。

$P$ の逆行列 $P^{-1}$ は
$P^{-1}= \begin{pmatrix} 1&-1\\ 0&1\\ \end{pmatrix}$
です。
では、 $P^{-1}AP$ を計算してみます。

$\begin{eqnarray} P^{-1}AP&=& \begin{pmatrix} 1&-1\\ 0&1\\ \end{pmatrix} \begin{pmatrix} 1&1\\ 0&2\\ \end{pmatrix} \begin{pmatrix} 1&1\\ 0&1\\ \end{pmatrix}\\ &=&\begin{pmatrix} 1&-1\\ 0&2\\ \end{pmatrix} \begin{pmatrix} 1&1\\ 0&1\\ \end{pmatrix}\\ &=& \begin{pmatrix} 1&0\\ 0&2\\ \end{pmatrix} \end{eqnarray}$
となって、対角化完了です。

結

今回は行列の対角化、どういうときに対角化可能なのか、ということについて解説しました。
対角化可能な条件は固有空間の次元、固有方程式の解の重複度、固有ベクトルと蜜に関係しているのでした。

特に、一番シンプルなのが、固有値がすべて相異なっている場合で、この場合は固有値を求めるだけで直ちに対角化後の行列が求まります。

次回は対角化を少し緩めた三角化について解説します。

乞うご期待！質問、コメントなどお待ちしております！

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34