本記事の内容
本記事は、基本情報技術者試験における2進数の四則演算、シフト演算について、情報及びコンピュータの素人目線から説明する記事です。
本記事を読むに当たり、2進数、16進数について知っている必要があるため、以下の記事も合わせてご覧ください。

本記事のゴール
本記事のゴールは次の問題をシフト演算で解けるようになることです。
10進数の演算式\(7\div 32\)の結果を2進数で表したものはどれか。
ア. 0.001011 イ. 0.001101 ウ. 0.00111 エ. 0.0111
(平成31年度)
2進数の四則演算
10進数の四則演算で慣れている我々は、2進数の四則演算を行おうとすると混乱します。
実際に筆者も混乱しました。
しかしながら、よくよく注意すれば加減法は問題ないし、積商も「シフト」の概念が分かればなんてことないのです。
2進数の加減
筆算で行います。
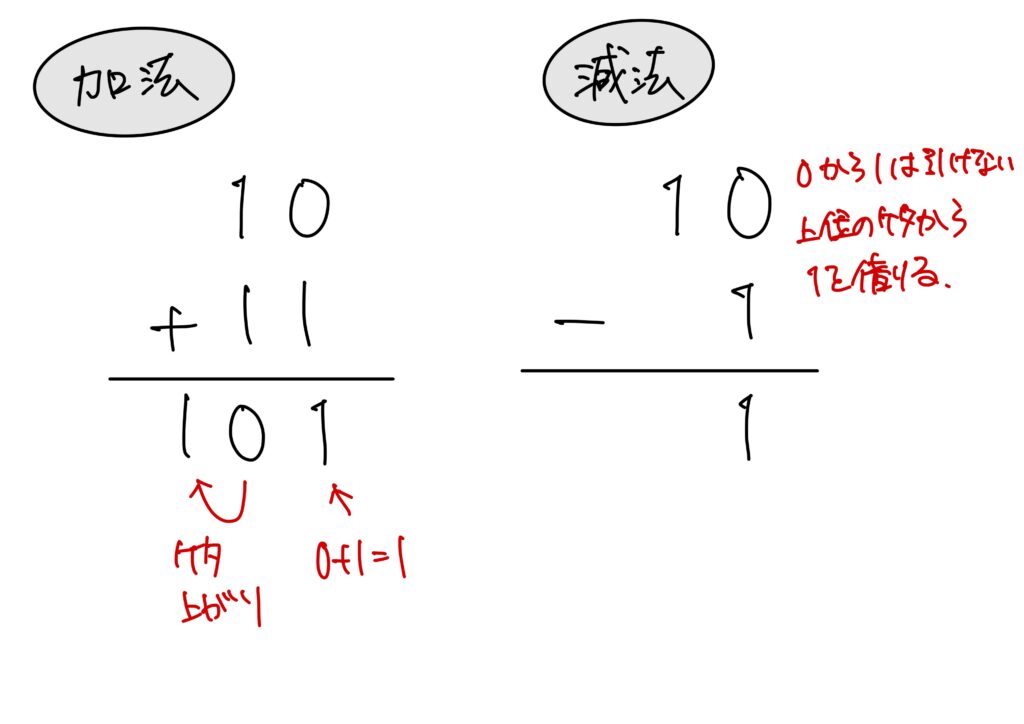
2進数の積商
2進数表現の数を一旦10進数に変換して計算し、計算結果を再び2進数にすることでも解けますが、時間と手間がかかります。
そこで有用なのが「シフト演算」です。
次の章で述べます。
シフト演算
シフト演算
シフト演算とは、ビットを左右にずらして、積及び商を行う計算方法のこと。シフト演算には、以下の2種類が存在します。
- 論理シフト:正負を考慮しない(符号ビットを考慮しない)
- 算術シフト:正負を考慮する(符号ビットを考慮する)
「ビットをずらす」とは?
10進数表現において357という数のビットを左にずらしてみましょう。
すると、3570となります。
つまり、10倍されています。
一方で右にずらしてみると、35.7となります。
これは\(\displaystyle\frac{1}{10}\)倍されています。
これは2進数でも同様で、「ビットをずらす」というのは、基数倍、基数分の1倍するという意味です。
すなわち、2進数表現においてビット列を\(n\)個分だけ左にずらすというのは、元の数を\(2^n\)倍すること、右にずらすというのは元の数を\(\displaystyle\frac{1}{2^n}\)倍するということになります。
論理シフト
ビット列を左右にずらした上で、
- ビット列からはみ出したビットを無視する。
- 空いたビットに「0」を入れる

算術シフト
論理シフトと異なり、符号を考慮するので、符号ビットを特別視して固定します。
つまり、符号ビットは据え置きで、それ以外のビットをずらす、というのが算術シフトです。
手順としては
- ビット列からはみ出したビットを無視する。
- 左方向にずらした場合は、空いたビットに0を入れる。
- 右方向にずらした場合は、符号ビットと同じ数を入れる。

シフト演算を使って本記事のゴールを解いてみる
10進数の演算式\(7\div 32\)の結果を2進数で表したものはどれか。
ア. 0.001011 イ. 0.001101 ウ. 0.00111 エ. 0.0111
(平成31年度)
\(32=2^5\)ですから、
$$
7\div32=7\div2^5=7\times\frac{1}{2^5}
$$
です。
\(7\)の2進数表現は111ですから、右に5ビットだけずらせば良いです。
故に、答えは0.00111です。
簡単にできましたね。
基本情報技術者試験では時間が厳しいので、このシフトを積極的に使うと良いようです。
結
今回は、基本情報技術者試験における2進数の四則演算、シフト演算について、情報及びコンピュータの素人目線から説明しました。
問題が解けるということに重きを置き説明しました。
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければお答えします!
Twitterでもリプ、DM問わず質問、コメントを大募集しております!



コメントをする