本記事の内容
本記事は「全射って何?」ということについて解説する記事である。
本記事を読むに当たり、「写像?」となっている方は以下の記事も合わせて御覧ください。
単射を知っていたほうが理解が進むと思われるので、その場合は以下の記事を参照してください。
全射
単射は「定義域の異なる要素は、対応する終域の要素も異なるような写像のこと。」だった。
単射の場合、終域の要素は全て使われていなくても良い(終域の要素に対応しない定義域の要素があっても良い)。
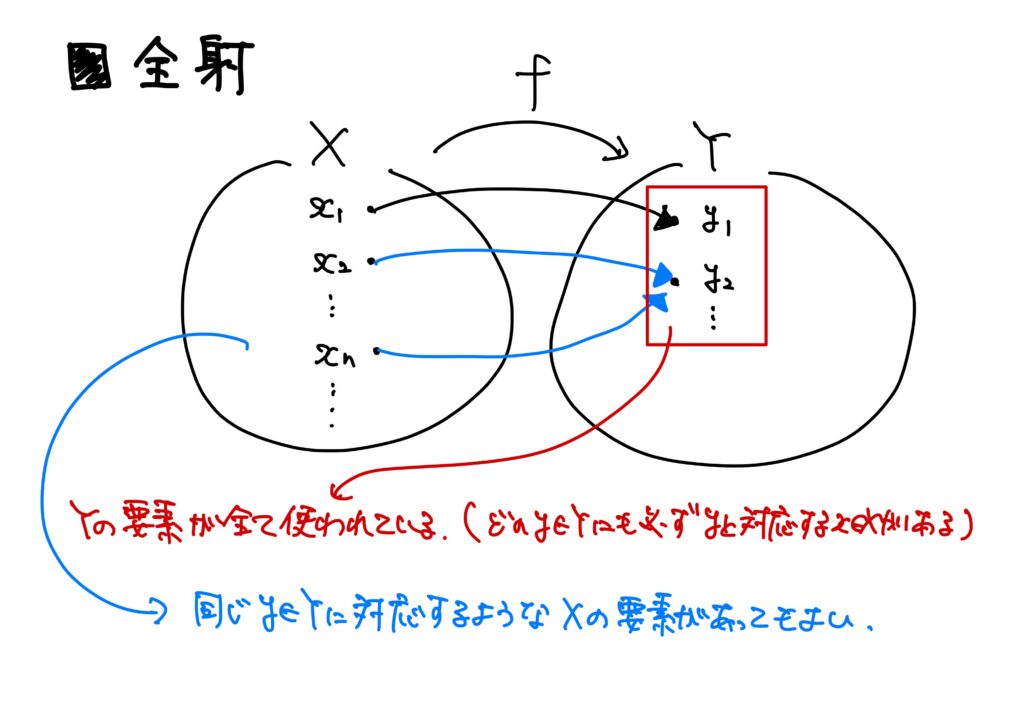
これに対して全射は「終域の要素が全て使われている写像」である。
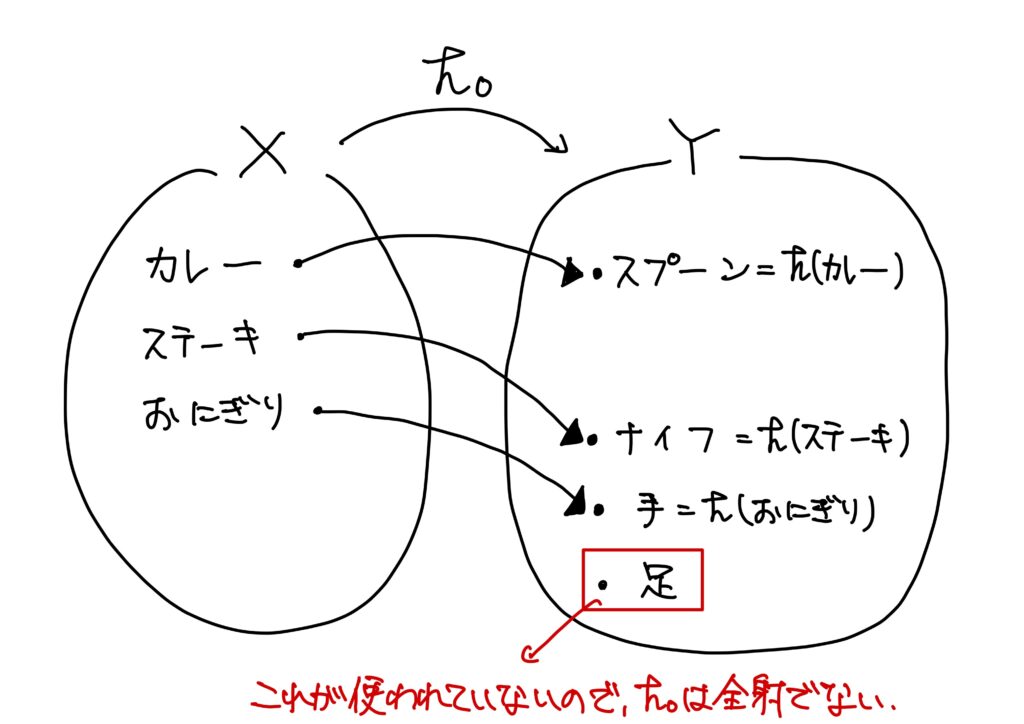
例1′.(料理を食べるときに使う食器との対応規則の改変ver.)
\(X’=\{カレー,ステーキ、おにぎり\}\)、\(Y’=\{スプーン,ナイフ,手,足\}\)とする。
このとき、写像\(h_0:X\to Y\)を
- \(h_0(カレー)=スプーン\)、
- \(h_0(ステーキ)=ナイフ\)、
- \(h_0(おにぎり)=手\)
で定める。
このとき、\(Y\)の要素であるスプーン、ナイフ、手にはそれぞれと対応するカレー、ステーキ、おにぎりという\(X\)の要素が存在する。
しかし、足\(\in Y\)と対応する\(X\)の要素は存在しない。
つまり、終域の要素が全て使われているわけではない(使われていない終域の要素が存在する)。
従って、この写像は全射ではない。
同様に例1.も全射ではない。
例2.(数学っぽい例)
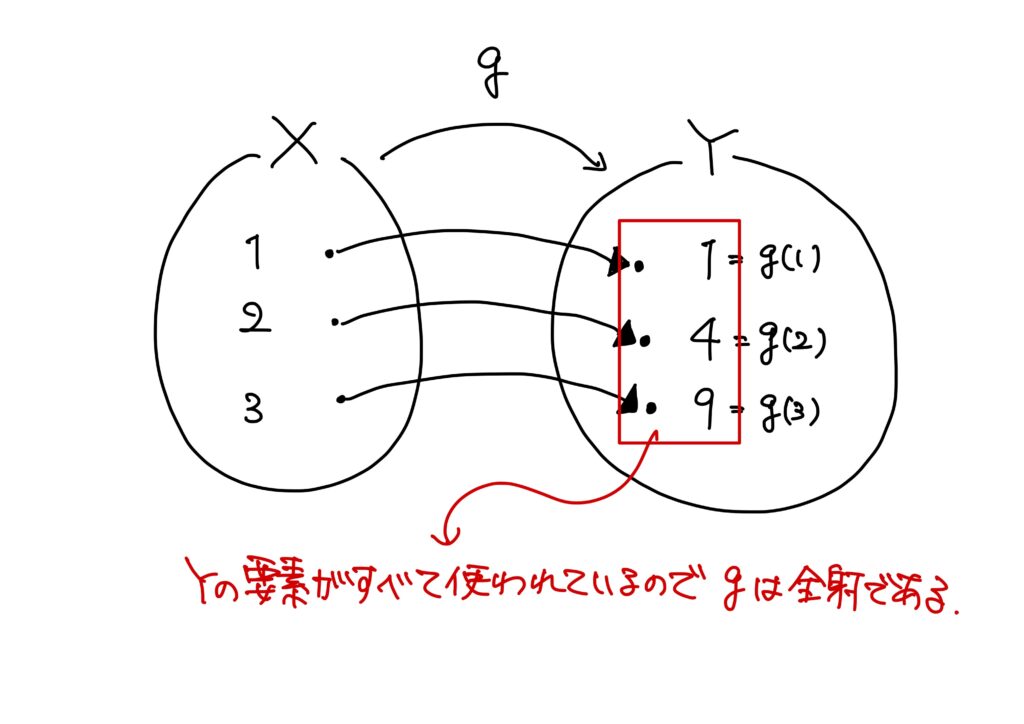
\(X=\{1,2,3\}\)、\(Y=\{1,4,9\}\)とする。
写像\(g:X\to Y\)を
- \(g(1)=1\)、
- \(g(2)=4\)、
- \(g(3)=9\)。
で定める。
このとき、終域\(Y\)の要素\(1,4,9\)には全て、それぞれに対応する定義域\(X\)の要素が存在する。
つまり、終域のすべての要素が使われている。
従って、\(g:X\to Y\)は全射である。
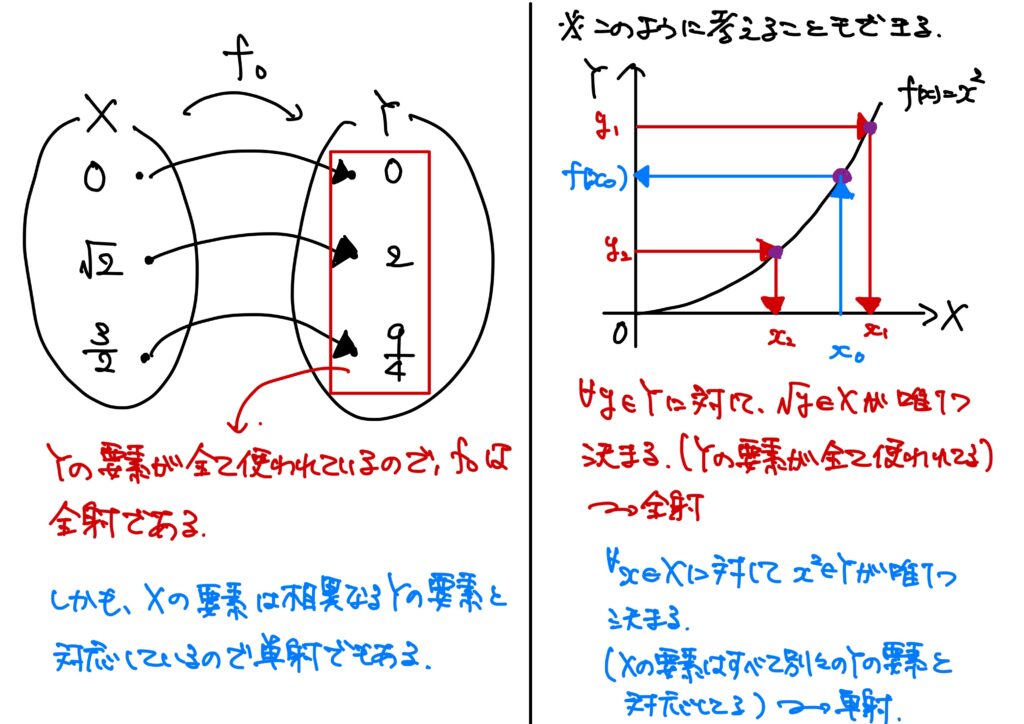
例3′.(実数値の関数のちょっと改変ver.)
\(X=Y=\{x\in\mathbb{R}\mid x\geq0\}\)とする。
このとき、写像\(f_0:X\to Y\)を\(f_0(x)=x^2\)で定める。
この\(f_0\)は全射である。
実際、任意の\(y\in Y\)に対して、\(\pm\sqrt{y}\in X\)が存在するからである。
ここで、この\(f_0\)は単射でもある。
なぜなら、任意の\(x_1,x_2\in X\)に対して、\(x_1\neq x_2\)ならば、\(f_0(x_1)=x_1^2\)であり、\(f_0(x_2)=x_2^2\)であるので、\(f_0(x_1)\neq f_0(x_2)\)であるからである。
一方、\(X=Y=\mathbb{R}\)とした例3.は全射ではない。
というのも、負の実数\(y\in Y=\mathbb{R}\)が対応する\(x\in X=\mathbb{R}\)が存在しないからである。
これを論理式で書けば、次である。
ここで1つ事実を述べる。
この証明はさほど難しくないので、是非挑戦してみてほしい。
(証明)
\(f:X\to Y\)を写像とする。
このとき、「\(f:X\to Y\)が全射\(\Rightarrow f(X)=Y\)」かつ「\(f(X)=Y\Rightarrow f:X\to Y\)が全射」が真であることを示せば良い。
①「\(f:X\to Y\)が全射\(\Rightarrow f(X)=Y\)」の証明
写像\(f\)が全射であるとする。
すなわち、
$$(\forall y\in Y)(\exists x\in X)\ {\rm s.t.}\ y=f(x)$$
が成り立っているとする。
このとき、
- \(f(X)\subset Y\),
- \(f(X)\supset Y\)
を示せば良い(※集合が等しいとはこういうことだった!論理と集合シリーズ その5を参照)。
- \(f(X)\subset Y\)について
$$(\forall y\in f(X)\Rightarrow y\in Y)$$
を示せば良い(※部分集合とはこういうことだった!論理と集合シリーズ その5参照)。
\(f(X)\)は\(f\)の値域であるので、
$$f(X)=\{f(x)\in Y\mid x\in X\}$$
である(写像って?を参照)。
任意の\(y\in f(X)\)に対して、\(f(X)=\{f(x)\in Y\mid x\in X\}\)なのだから、\(y=f(x)\)と書ける。
\(f(x)\)は\(x\in X\)と対応する\(Y\)の要素を指すのだから、\(f(x)\in Y\)である。
すなわち、\(y\in Y\)である。
※この1.は、\(f\)が全射でなくとも、写像であれば常に成り立つ。 - \(f(X)\supset Y\)について
$$(\forall y\in Y\Rightarrow y\in f(X))$$
を示せば良い。
\(f\)が全射であるため、
$$(\forall y\in Y)(\exists x\in X)\ {\rm s.t.}\ y=f(x)$$
が成り立っている。
すなわち任意の\(y\in Y\)に対して、\(y=f(x)\)を満たす\(x\in X\)を見つけてこれる。
\(f(X)=\{f(x)\mid x\in X\}\)なのだから、\(f(x)\in f(X)\)である。
従って、\(y\in f(X)\)である。
故に、\(f:X\to Y\)が全射\(\Rightarrow f(X)=Y\)である。
②「\(f(X)=Y\Rightarrow f:X\to Y\)が全射」の証明
\(f(X)=Y\)とする。
このとき
$$(\forall y\in Y)(\exists x\in X)\ {\rm s.t.}\ y=f(x)$$
を示せば良い。
すなわち、上記を満たすような\(x\in X\)を見つけてきなさい、ということである。
今、\(f(X)=Y\)なのだから、任意の\(y\in Y\)に対して、\(y\in f(X)\)である(\(f(X)\subset Y\)かつ\(f(X)\supset Y\)だから)。
従って、ある\(x_0\in X\)が存在して、\(y=f(x_0)\)である。
\(x\)として先程見つけた\(x_0\)を採用すれば、任意の\(y\in Y\)に対して、ある\(x\in X\)が存在して、\(y=f(x)\)を満たす。
従って、
$$(\forall y\in Y)(\exists x\in X)\ {\rm s.t.}\ y=f(x)$$
が成り立つ。
故に「\(f(X)=Y\Rightarrow f:X\to Y\)が全射」が成り立つ。
以上により、
$$f:X\to Yが全射\Leftrightarrow f(X)=Y$$
である。
(Q.E.D.)
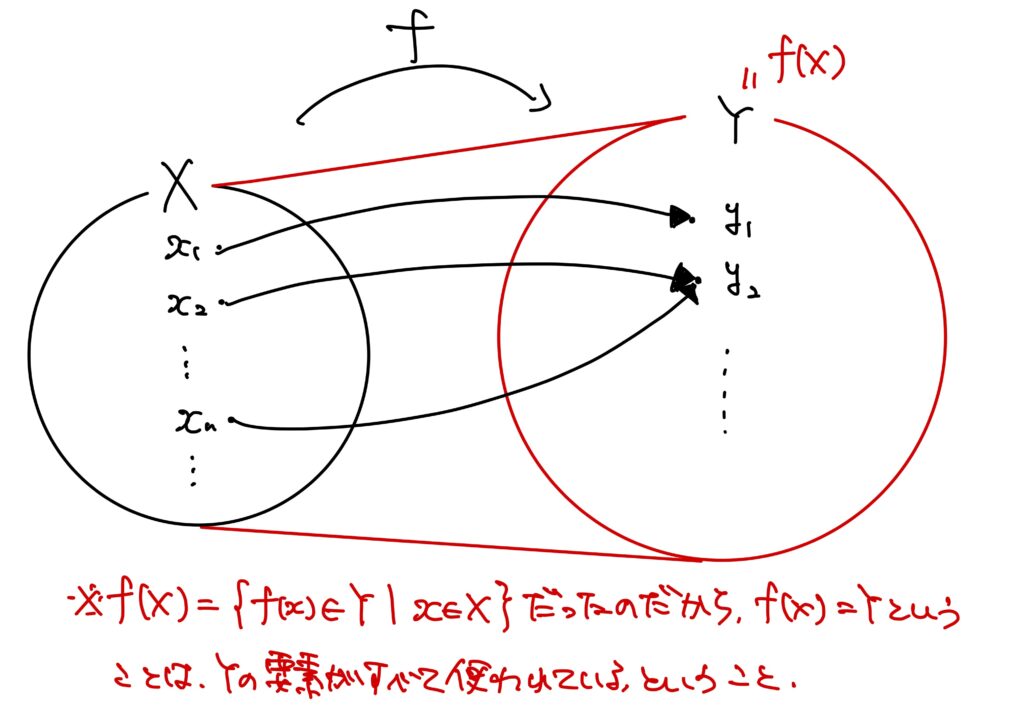
この命題により、「写像\(f:X\to Y\)が全射と言われたらば、\(f(X)=Y\)のことだ!」と思って良いわけである。
\(f(X)\)は任意の\(x\in X\)に対してその\(x\)と対応する\(Y\)の要素の集合なのだから、\(f(X)=Y\)ということは、\(Y\)の要素が全部使われているということなのである。
結
今回は全射について解説した。
全射は終域のすべての要素が使われている(終域のすべての要素に対応がある)ような写像である。
また、全射であることと、終域が定義域の順像と一致していることは同値である。
従って、「全射とは終域が定義域の順像と一致している写像のこと」と思ってもらって構わない。
次回は、「全単射」について解説する。
全単射は逆写像(逆関数)を語る上で必要不可欠な概念である。
乞うご期待!質問、コメントなどお待ちしております!





コメントをする