本記事の内容
本記事は写像に対する基本的な諸概念の説明をする記事である。
今回は、定義域、終域、順像、逆像、写像の相等について説明する。
「写像?」「どんなのが写像なの?」となっている方は以下の記事を御覧ください。
「写像って数学的に何?」という方は以下の記事を御覧ください。
写像\(f:X\to Y\)に付随する概念の名称
定義域、終域
\(f:X\to Y\)を写像とする。
- \(f(x)\)を\(f\)による\(x\)の像(the image of \(x\) under \(f\))、\(f\)の\(x\)における値(the mapping value at \(x\))という。
- \(X\)を写像\(f\)の定義域(the domain of \(f\), the domain of definition of \(f\))という。他に、始域、始集合と呼ぶこともある。
- \(Y\)を写像\(f\)の終域とよぶ。
順像および逆像
例1.について、\(X=\{カレー,ステーキ,おにぎり,チャーハン\}\)、\(Y=\{スプーン,ナイフ,手,足\}\)であった。
このとき、\(h:X\to Y\)は
- \(h(カレー)=スプーン\)、
- \(h(ステーキ)=ナイフ\)、
- \(h(おにぎり)=手\)、
- \(h(チャーハン)=スプーン\)
としたのだった。
これは、集合\(X\)の任意の要素が集合\(Y\)の部分集合\(\{スプーン,ナイフ,手\}\)の要素と対応がある、と捉えることができる。
更にいえば、\(X\)の部分集合\(\{カレー,おにぎり\}\)の任意の要素が集合\(Y\)の部分集合\(\{スプーン,手\}\)の要素と対応がある、というように部分集合の対応先も考えることができる。
このように、\(X\)の部分集合\(A\)の任意の要素\(a\in A\subset X\)と対応する\(y\in Y\)の要素の集合を順像(the image of \(A\) under \(f\))という。
特に、\(A=X\)である場合、すなわち、任意の\(x\in X\)に対して、それらと対応する\(y\in Y\)の要素の集合は値域(the range of \(f\))という。
言ってしまえば、順像は\(x\in X\)のときの\(f(x)\)を要素とする集合だ、というわけである。
ちなみに、高校数学で学ぶであろう関数の値域は、関数を写像とみなしたとき、ここで言うところの値域なのである。
一方で、順像とは逆の集合もある。
\(Y\)の要素と対応する\(X\)の要素の集合、ということである。
\(Y\)の部分集合\(\{ナイフと手\}\)の要素であるナイフと手はそれぞれ、\(X\)の部分集合\(\{ステーキ,おにぎり\}\)の要素と対応がある。
すなわち、終域の対応されている要素に対して、その一部(または全体)と対応している定義域の要素の集合を考えることもできる。
このようにこのように、\(Y\)の部分集合\(B\)の任意の要素\(b\in B\subset Y\)と対応する\(x\in X\)の要素の集合を逆像(the inverse image of \(B\))という。

以上のことを記号を使って書けば、次である。
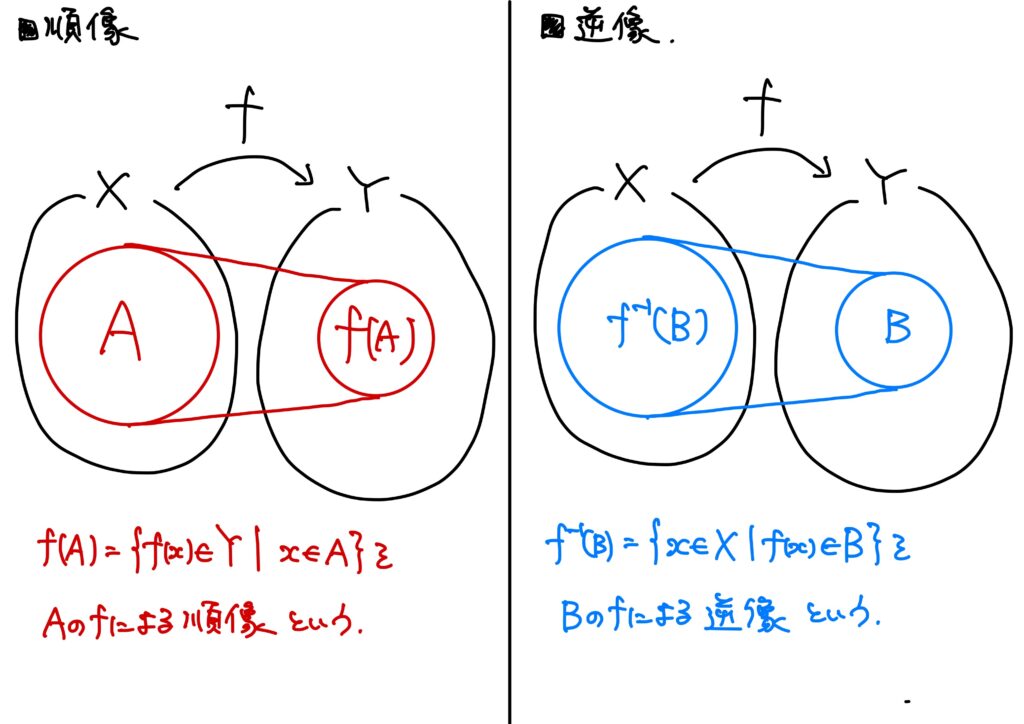
- 順像 \(X\)の部分集合\(A\)(\(A\subset X\))に対して、 $$f(A)=\{y\mid (\exists x\in A)\ {\rm s.t.}\ y=f(x)\}=\{f(x)\mid x\in A\}$$ を\(A\)の\(f\)による順像(または単に像、the image of \(A\) under \(f\))とよぶ。 特に、定義域\(X\)の\(f\)による順像(\(A=X\)のときの順像) $$f(X)=\{y\mid (\exists x\in X)\ {\rm s.t.}\ y=f(x)\}=\{f(x)\mid x\in X\}$$ を単に\(f\)の像(the image of \(f\))、あるいは値域(the range of \(f\))といい、\({\rm Image}(f)\)と表すこともある。
- 逆像 \(Y\)の部分集合\(B\)に対して、\(f\)による順像\(B\)に属するような\(X\)の要素の集合、すなわち $$f^{-1}(B)=\{x\in X\mid f(x)\in B\}$$ を\(B\)の\(f\)による逆像(the inverse image of \(B\), pull-back)という。
2つの写像が等しいって?
今までは1つの写像について話してきた。
一旦、複数の写像について、特に2つの写像についての諸概念を述べる。
今まで挙げた例1,2,3はどれも写像として一致しない。
「対応させるモノが違うんだからそりゃそうでしょ」と言う気もするのだが、こんな例はどうだろうか。
例4.(写像の一致)
\(X=\{1,2,3\}\)、\(Y=\{4,5\}\)とする。
これらの集合に対する写像\(f:X\to Y\)を\(f(1)=f(2)=4\)、\(f(3)=5\)で定める。
新たに、\(g:X\to Y\)を\(g(x)=\max\{x+2,4\}\)、すなわち、\(x\in X\)に対して、\(x+2\)と\(4\)のうち大きい方を\(g(x)\)の値として採用するとする。
すると、
$$g(1)=\max\{1+2,4\}=4,\ g(2)=\max\{2+2,4\}=4,\ g(3)=\max\{3+2,4\}=5$$
となる。
さらに、
\(h:X\to Y\)を\(\displaystyle h(x)=\left[\frac{x+7}{2}\right]\)(ただし、\([]\)はGauss記号)として\(h\)を定めれば、
$$h(1)=\left[\frac{8}{2}\right]=4,\ h(2)=\left[\frac{9}{2}\right]=4,\ h(3)=\left[\frac{10}{2}\right]=5$$
である。
従って、対応させるための規則は\(f,g,h\)でそれぞれ異なっているが、対応する数は一致している。
このとき、\(f,g,h\)は一致する、というのが写像が等しいということである。
つまり、2つの写像に対して、対応させる規則が異なっていたとしても、定義域と終域と対応するモノが一致しているとき、それらは等しいというのだ。
これを論理式で書くと次である。
2つの写像\(f_1:X_1\to Y_1\)と\(f_2:X_2\to Y_2\)が等しいとは、 $$(X_1=X_2)かつ(Y_1=Y_2)かつ((\forall x\in X_1)\ f_1(x)=f_2(x))$$ が成り立つことをいう。
とどのつまり、2つの写像が等しいというのは、「定義域と終域が一致していて、各要素は2つの写像で同じ要素と対応している」状態のことを言うわけである。
結
今回は、写像に対する諸概念の解説をした。
勿論、今回解説したもの以外にもあるのだが、基本は今回解説したものである。
注意なのが、順像および逆像は集合である、ということだ。
そして、「どっちがどっち?」となりやすい側面もある。
「対応する前の要素の集合か対応後の集合か」(出発点か行き先か、という言い方もする)をハッキリさせることが重要である。
また、写像が等しいというのは、定義域と終域が一致していて、各要素が②つの写像で同じ要素と対応している状態のことをいう。
つまり、2つの写像の対応規則が一見異なっていても、これらが一致すると写像としては一致すると決めます、というのが写像の相等である。
次回は、2つの写像を”合わせた”、すなわちある写像で対応させた後に別の写像で対応させる写像を解説する。
これを合成写像という。
乞うご期待!質問、コメントなどお待ちしております!






コメントをする