本記事の内容
本記事は「数学の文章って何言ってるかわかんない」、「論理的ってどういうこと?」、「数学の勉強をしてみたいけど、何が書いてあるか読めない」という方向けである。
前回から集合についてのトピックスを解説している。
前回の記事では「集合って?」、「書き方は?」についてを解説した。
今回は複数の集合の関係性から数学でよく出現する集合について解説する。
「集合って?」となっている方は以下(前回の記事)をご参照ください。

序
前回の記事で「数学は集合の言葉で書かれていると言っても過言ではない」と述べた。
若干厳密に言えば、数学は集合と写像の言葉で書かれている、というべきなのだが、このシリーズでは写像は解説しない。
(某論破王の影響で「写像」という言葉は知っているかもしれないが、その写像ではない。)
前回は部分集合、集合の相等という2つの集合の関係性の一部を解説したのだが、数学に出現する集合及び複数の集合の関係性はこれだけではない。
勿論沢山あるわけだが、それを全て解説することは難しいので、特によく出現する集合について解説する。
一言で述べれば、本記事は“和”、”差”、”積”に対応する集合について述べる。
“商”に対応する集合もあるのだが、和、差、積に比べてジャンプがあるため、次回解説する。
また、集合を直感的に、視覚的に理解するためのベン図についても解説する。
ベン図
「ベン図って何?」について解答しよう。
とはいえ、実は高校数学ですでに出現しているため、簡単な解説に留めることにする。
ベン図は複数の集合の関係性を模式的に表した図のことで、含み含まれる関係、複数の集合をあわせた集合、複数の集合の共通な部分などを視覚的に表した以下のような図である。
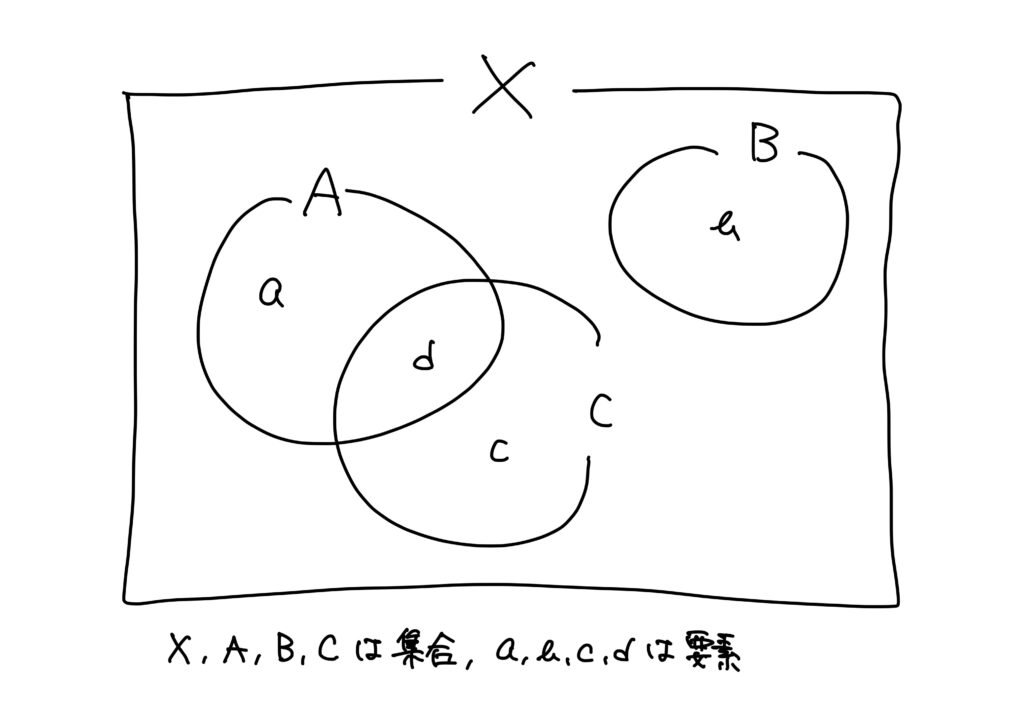
前回の例を流用すると、
- \(X\):人間全体の集合
- \(A\):日本人全ての集合
- \(B\):アメリカ人全ての集合
は

となる。
数学の例を挙げれば、
- \(\mathbb{N}\):自然数全体の集合
- \(A\):\(6\)の倍数の集合
- \(B\):\(2\)の倍数の集合
- \(C\):\(3\)の倍数の集合
とすると、ベン図は以下のようになる。
重なっている部分は\(B\)の要素でもあり、\(C\)の要素でもある、という意味で、共通部分という。(後述)
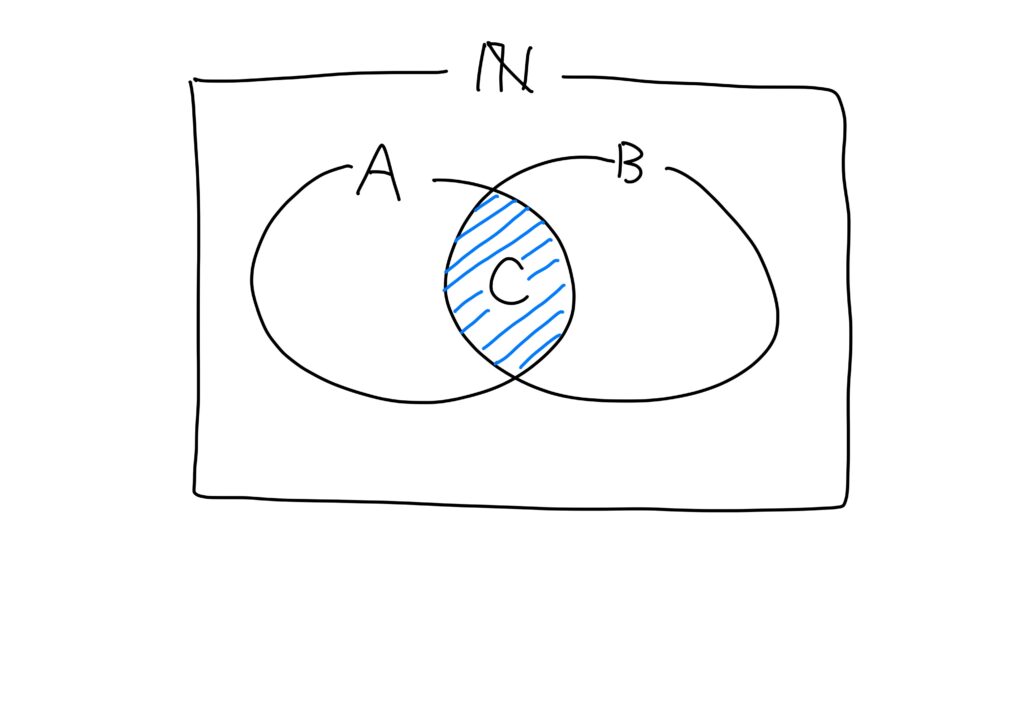
一番外側の集合は「全体集合」とも呼ばれる。
ここで注意なのが、なにか集合についての証明を与えるとき、ベン図はその根拠にはなりえない。
というのも、証明というのは論理的に正しいことを示すことなのであって、あくまでベン図は題意を視覚的に理解するための補助であるから、論理的な対象ではない。
従って、定理やらの証明を理解するための補助とはなり得るが、根拠にはならない。
あくまで、論理的に示す必要がある。
和集合
例えば、「カレーが好きな人とラーメンが好きな人は合わせてどれくらいいるのかな?」となったとき、「じゃあ、カレーが好きな人の集合とラーメンが好きな人の集合を考えればいいよね?」となる。
つまり、カレーが好きな人の集合とラーメンが好きな人の集合を”合わせた”集合を考えるとよい、ということになる。
このように、複数の集合を”合わせた”集合を考えることもしばしばある。
2つの集合を”合わせた”(足し算ではない)集合のことを和集合(sum)、合併(合併集合、the union of two sets)という。
例1.
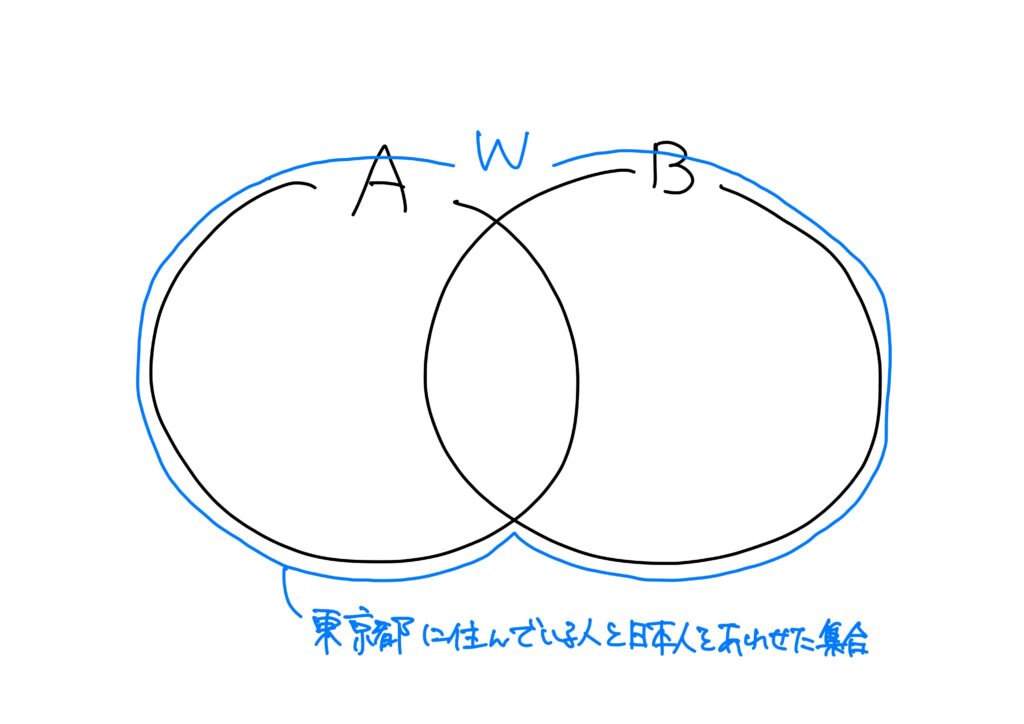
- \(A\):東京都に住んでいる人の集合
- \(B\):日本人の集合
- \(W\):\(A\)と\(B\)の和集合
とするとき、\(A\)と\(B\)の和集合\(W\)は「東京都に住んでいる人と日本人をあわせた集合」となる。
より論理っぽく書けば、「東京都に住んでいるまたは日本人である、という条件を満たす要素からなる集合」となる。
ベン図では以下のように書かれる。
例2.
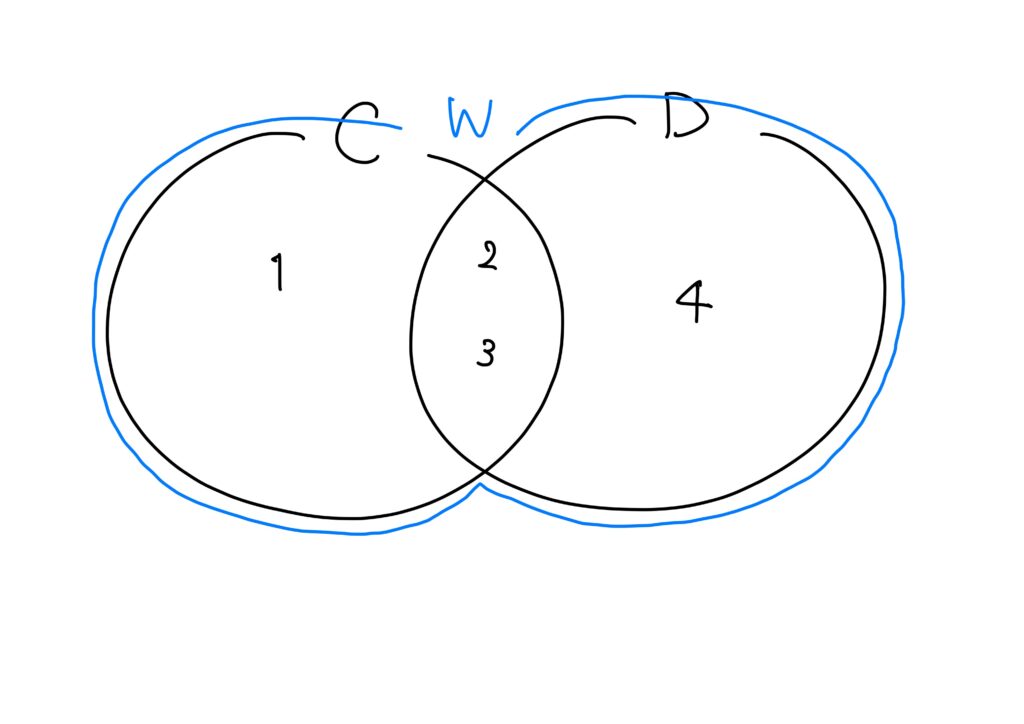
\(C=\{1,2,3\}\)、\(D=\{ 2,3,4 \}\)とするとき、\(C\)と\(D\)の和集合\(W\)は\(\{1,2,3,4\}\)である。
例3.
- \(E\):\(6\)の倍数の集合
- \(F\):\(5\)の倍数の集合
- \(W\):\(F\)と\(G\)の和集合
とするとき、\(E\)と\(F\)の和集合\(W\)は「\(6\)か\(5\)で割り切れる整数の集合」となる。
より論理っぽく書けば、「\(6\)で割り切れるまたは\(5\)で割り切れる、という条件を満たす要素からなる集合」となる。
ベン図では以下のように書かれる。

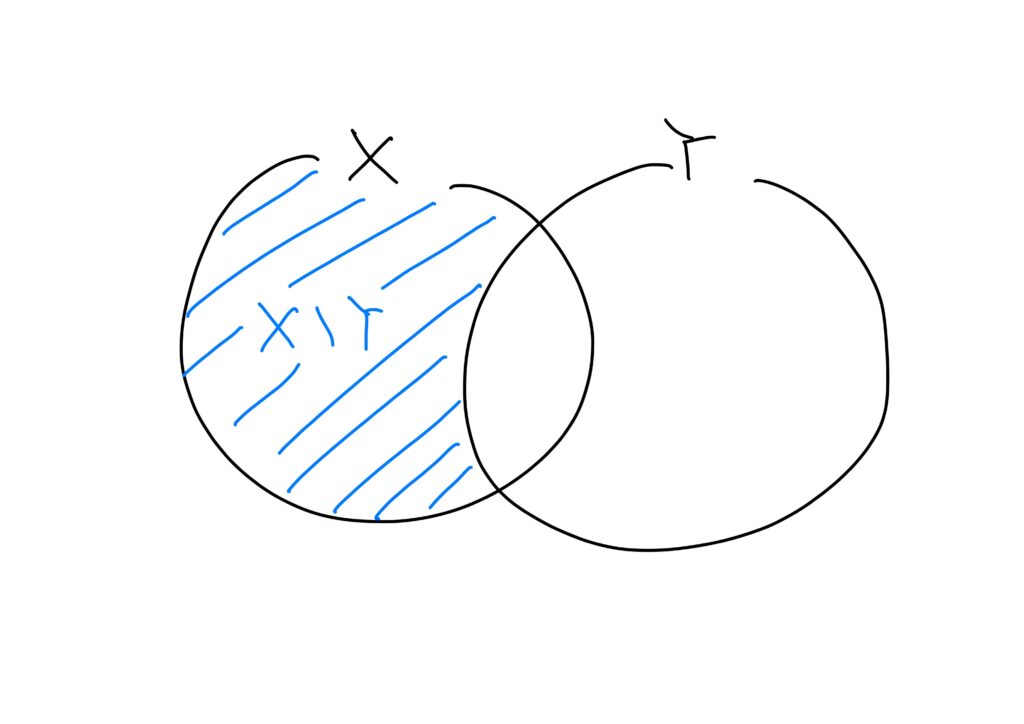
上記の例を念頭に入れれば、集合\(X\)と\(Y\)の和集合は
$$x\in X または x\in Yが成り立つようなxの集合$$
ということに気がつくことだろう。
これを厳密な論理式で書くと次になる。
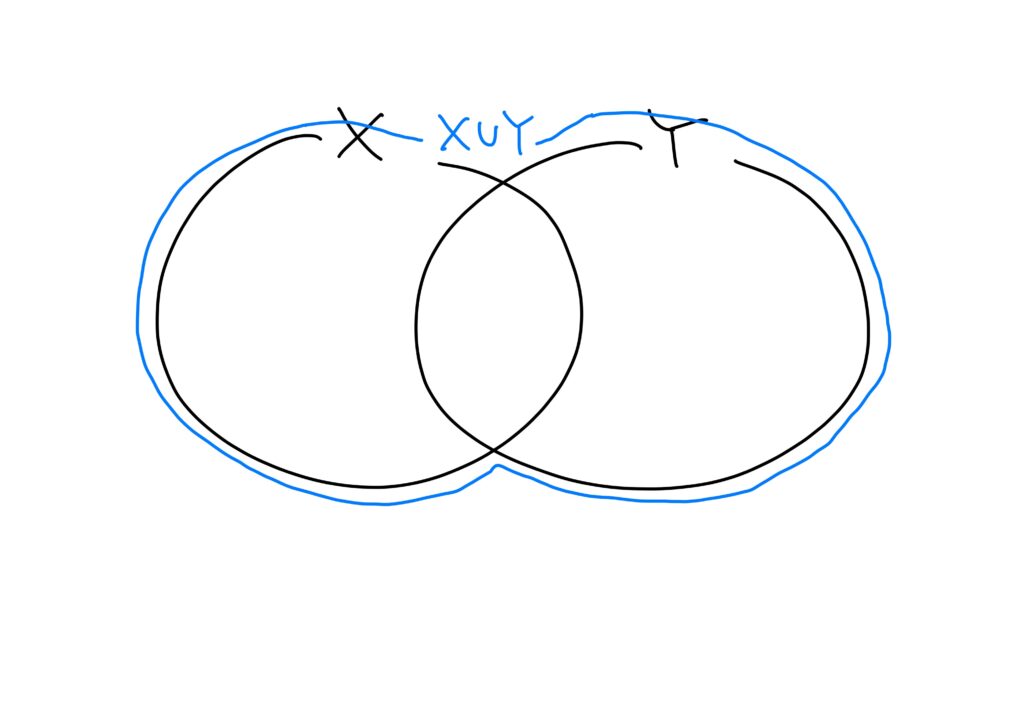
しばしば\(\cup\)をカップ(cup)と読む。
コーヒーカップのカップであり、1つの容器に入れる、というイメージを持つと覚えやすいかもしれない。
また、常に\(X\subset X\cup Y\)および\(Y\subset X\cup Y\)が成り立つ。
我々はすでに論理を学んでいるため、\(X\cup Y\)の要素\(x\)は\(x\in X\)と\(x\in Y\)が同時に成り立っても良い、ということがわかる。
つまり、\(x\in X\land x\in Y\)が成り立っても、\(x\in X\cup Y\)の要素である。
一方で、\(x\in X\land Y\)が成り立つような\(x\)の集合を集合\(X\)と\(Y\)の共通部分という。
共通部分
例えば、「カレーとラーメンの両方が好きな人ってどれくらいいるのかな?」となったとき、「カレーが好きな人の集合とラーメンが好きな人の集合の共通した部分の集合を考えればよいよね?」となる。
このように、複数の集合の共通部分を考えることもしばしばある。
前節の通り、2つの集合の共通している部分もまた集合であり、その集合を共通部分(交わり、the intersection of two sets)という。
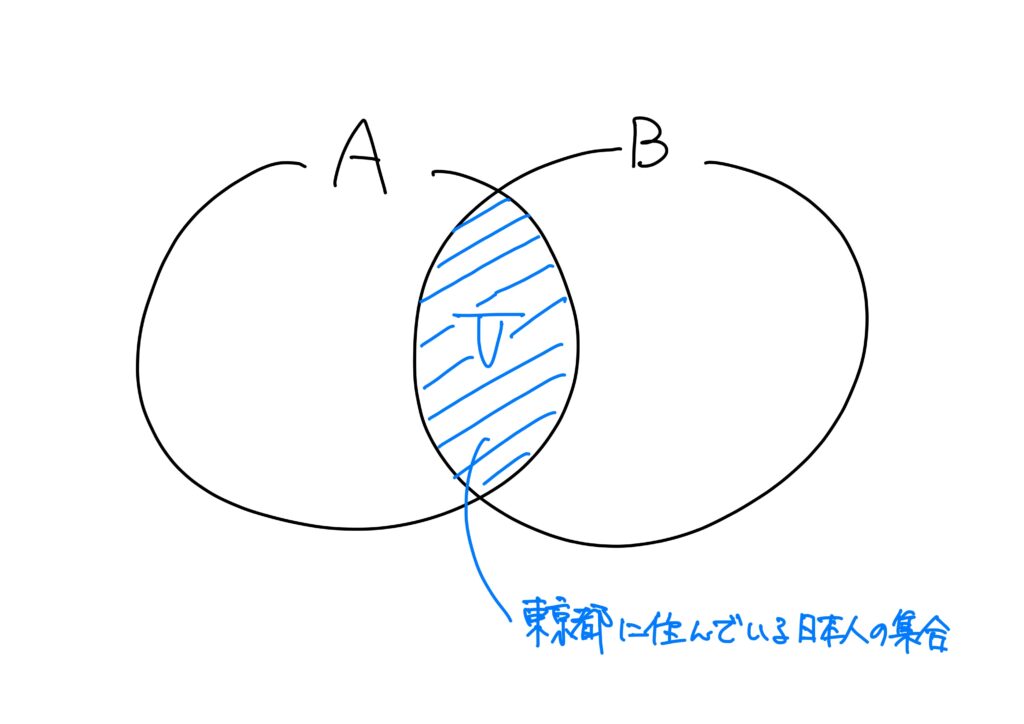
例1.
- \(A\):東京都に住んでいる人のグループ
- \(B\):日本人のグループ
- \(V\):\(A\)と\(B\)の共通部分
とするとき、\(A\)と\(B\)の共通部分\(V\)は「東京都に住んでいる日本人の集合」となる。
より論理っぽく書けば、「東京都に住んでいるかつ日本人である、という条件を満たす要素からなる集合」となる。
ベン図では以下のように書かれる。
例2.
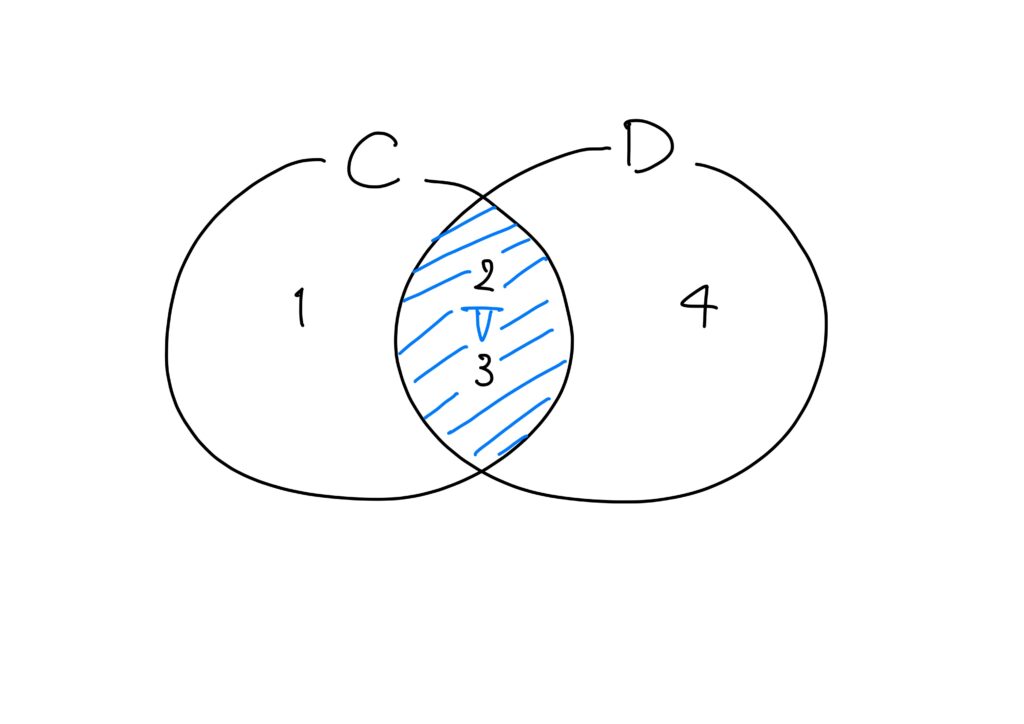
\(C=\{1,2,3\}\)、\(D=\{ 2,3,4 \}\)とするとき、\(C\)と\(D\)の共通部分\(V\)は\(\{2,3\}\)である。
例3.
- \(E\):\(6\)の倍数の集合
- \(F\):\(5\)の倍数の集合
- \(V\):\(E\)と\(F\)の共通部分
とするとき、\(E\)と\(F\)の共通部分\(V\)は「\(6\)でも\(5\)でも割り切れる整数の集合」となる。
より論理っぽく書けば、「\(6\)で割り切れるかつ\(5\)で割り切れる、という条件を満たす要素からなる集合」となる。
ベン図では以下のように書かれる。

上記の例を念頭に入れれば、集合\(X\)と\(Y\)の共通部分は
$$x\in X かつx\in Yが成り立つようなxの集合$$
ということに気がつくことだろう。
これを厳密な論理式で書くと次になる。

しばしば\(\cap\)をキャップ(cap)と読む。
帽子のキャップであり、”かぶっている部分”というイメージを持つと覚えやすいかもしれない。
また、常に\(X\cap Y \subset X\)および\(x\cap Y\subset Y\)が成り立つ。
\(\cup\)と\(\cap\)についての法則
論理と同様に、和集合、共通部分についても法則がある。
結論から言ってしまえば、和集合だけ、共通部分だけ(つまり\(\cup\)だけ、\(\cap\)だけ)の場合は順序は関係ないが、和集合と共通部分が同時に出てくる(\(\cup\)と\(\cap\)が同時に出てくる)場合だけ注意が必要である。
- 交換法則:\(X\cup Y=Y\cup X\)、\(X\cap Y=Y\cap X\).
- 結合法則:\(X\cup(Y\cup Z)=(X\cup Y)\cup Z\)、\(X\cap (Y\cap Z)=(X\cap Y)\cap Z\).
- 分配法則:\(X\cup (Y\cap Z)=(X\cup Y)\cap (X\cup Z)\)、\(X\cap (Y\cup Z)=(X\cap Y)\cup(X\cap Z)\)
これらは全て、論理の交換法則、結合法則、分配法則から導かれれる。
交換法則、結合法則については明らかなので、省略するが、分配法則についてはベン図を用いて説明する。

差集合
2つの集合\(X\)と\(Y\)に対して和集合を考えた。
これを集合におけるある種の”和”と捉えれば、”差”に対応する集合もある。
例えば、「カレーは好きじゃないだけど、ラーメンは好きな人ってどれくらいいるのかな?」となったとき、「ラーメンが好きな人の集合からカレーが好きな人を取り除いた集合を考えればいいよね?」となる。
それが差集合である。
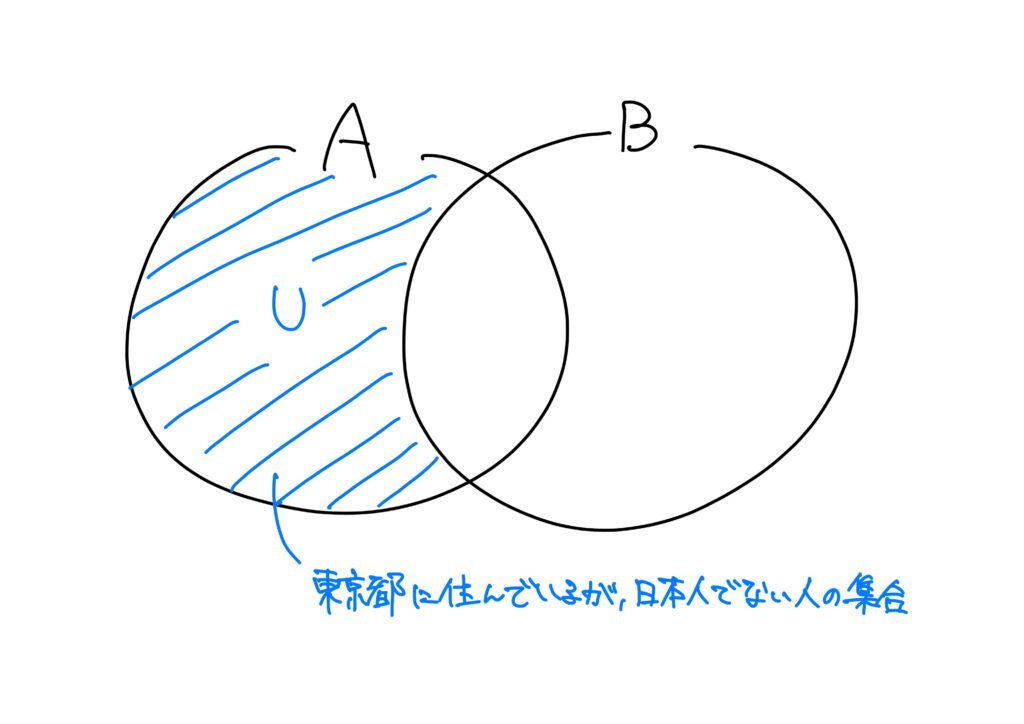
例1.
- \(A\):東京都に住んでいる人のグループ
- \(B\):日本人のグループ
- \(U\):\(A\)から\(B\)を取り除いた集合
とすると、\(A\)から\(B\)を”取り除いた”集合\(U\)は「東京都に住んでいるが、日本人でない人の集合」である。
例2.
\(C=\{1,2,3\}\)、\(D=\{ 2,3,4 \}\)とするとき、\(C\)から\(D\)を”取り除いた”集合\(U\)は\(\{1\}\)である。

例3.
- \(E\):\(6\)の倍数の集合
- \(F\):\(5\)の倍数の集合
- \(U\):\(E\)から\(F\)を取り除いた集合
とすると、\(E\)から\(F\)を”取り除いた”集合\(U\)は「\(6\)の倍数だが、\(5\)の倍数でない整数の集合」である。

つまり、集合\(X\)と\(Y\)の差集合は
$$x\in X\land x\not \in Yが成り立つようなxの集合$$
である。
これを論理式で書けば、次になる。
この論理式を見れば、直感的に分かることだが、\(X\cap Y=\emptyset\)(共通部分に要素が1つもない)の場合、\(X\setminus Y=X\)であり、\(Y\setminus X=Y\)である。
「神奈川県横浜市出身の人の集合から神奈川県川崎市出身の人の集合を取り除いたところで、横浜市出身の人の中に川崎市出身の人はいないのだから、結局横浜市出身の人の集合だよね」というわけである。
また、\(X\setminus \emptyset=X\)である。これは「どんな数から\(0\)を引いても元の数だよね」に対応する。
補集合
例えば、「ご飯物が好きな人の中で、カレーが好きでない人ってどれくらいいるのかな?」となったとき、”以外の”に対応する集合を対象として考察することになる。
勿論、これは結果的に差集合なのだが、”以外の”に対応する集合には特別補集合という名前をつけている。
ただ、上記の差集合と異なる点は、差集合は対象がどんな2つの集合であっても良いが、補集合は含み含まれる関係(部分集合の関係)にある集合が対象だ、ということである。
実際、先の例はカレーはご飯物であるから、カレーが好きな人の集合はご飯物が好きな人集合の部分集合である。
要は、”ある〇〇の中で△△でないところ”やら”ある〇〇の中で△△以外のところ”に対応する集合だ、ということである。
この「ある〇〇の中で」の文言があるか否かがミソである。(とはいえ、結局補集合は差集合を使って決めるのだがネ)
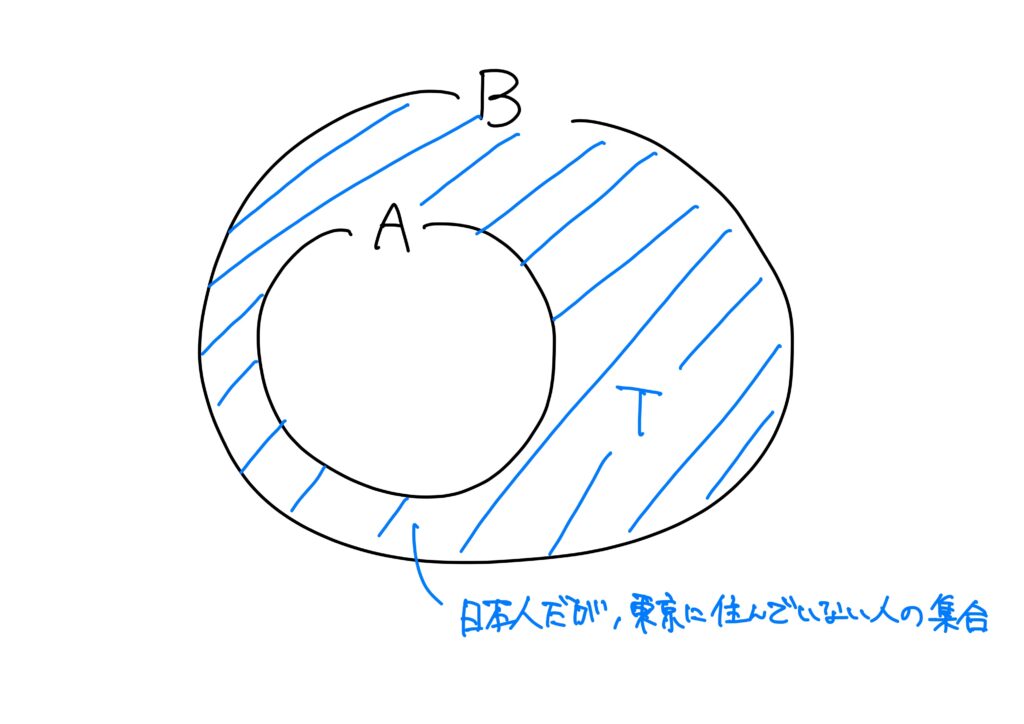
例1.
- \(A\):東京都に住んでいる日本人のグループ
- \(B\):日本人のグループ
- \(T\):\(B\)の中で\(A\)以外の人の集合
とすると、\(A\subset B\)であり、\(B\)の中で\(A\)以外の人の集合\(T\)は「日本人だが、東京に住んでいない人の集合」である。
(「え、結果差集合じゃんね。」と思う気持ちも分かるが、後述するのでちょっとこらえてほしい)
例2.
\(C=\{1,2,3\}\)、\(D=\{ 2,3,4 \}\)とするとき、\(C\)と\(D\)は\(C\not\subset D\)であり\(D\not\subset C\)であるため、これらには補集合は考えられない。
例3.
- \(E\):\(6\)の倍数の集合
- \(F\):\(5\)の倍数の集合
とすると、これも同様で、\(E\not\subset F\)かつ\(F\not\subset E\)であるため、これらには補集合は考えられない。
最も、\(E\)と\(F\)よりも大きい(外側)の集合として\(\mathbb{N}\)を考える、とまで言えば補集合は考えられるが、これら2つの集合については補集合は決められない。
例4.
- \(G\):\(10\)の倍数の集合
- \(H\):\(20\)の倍数の集合
- \(T\):\(G\)の中で\(H\)でない整数の集合
とすると、\(H\subset G\)であるから、\(G\)の中で\(H\)でない整数の集合\(T\)は「\(10\)の倍数だが、\(20\)の倍数ではない(たとえば\(30\))整数の集合」となる。

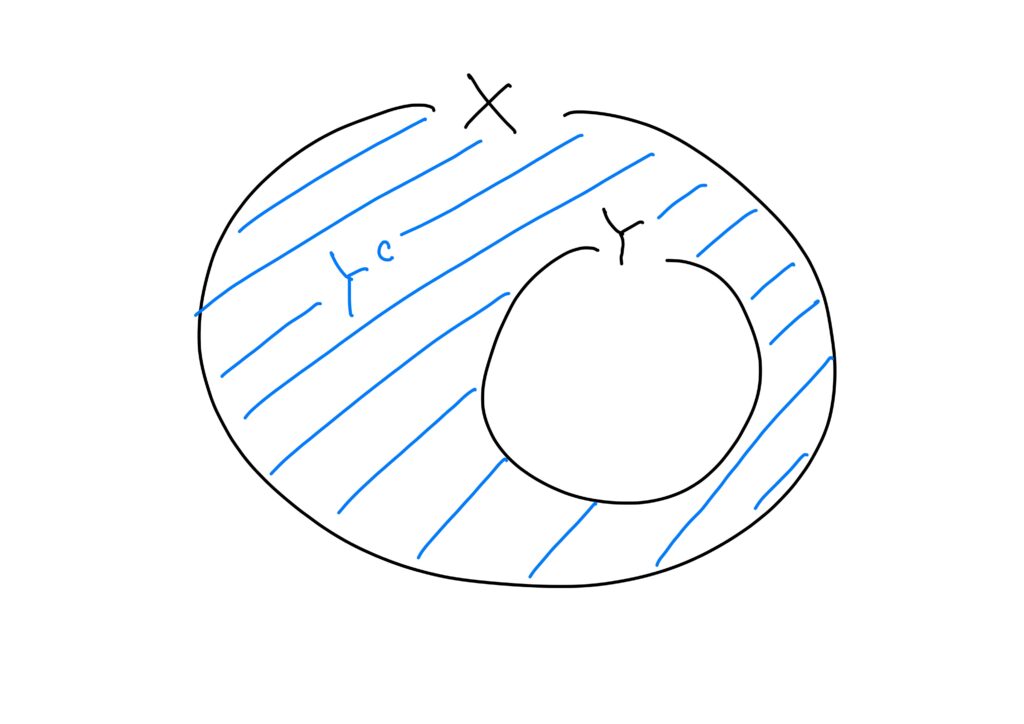
つまり、集合\(X\)と\(Y\)で、\(Y\subset X\)を満たしているとき、\(X\)における\(Y\)の補集合\(Y^c\)は
$$Y\subset Xのとき、 x\in X\land x\not\in Yを満たすようなxの集合$$
である。
これを論理式で表せば、次になる。
ここで、記号についてなのだが、\(\bar{Y}\)は\(Y\)の補集合としても使われる(高校数学ではこの記号だったと思われる)が、\(\bar{Y}\)は\(Y\)の補集合としてよりも\(Y\)の閉包(解析学でよく出現する)として使われる場合が多いので、本記事では\(Y\)の補集合を\(Y^c\)と書くことにする。
さて、「結局差集合やないかーい」ということについてだが、条件「\(Y\subset X\)」があると無いとでは大きく話が変わる。
例えば単に「日本人以外の集合ってどんな集合?」と言われたら「まあ、アメリカ人とかイギリス人とか中国人とかの集合じゃない?」と思うだろう。
しかしこれはあくまで「”人間の集合の中で”という言葉が省略されてるだけだよね」と我々が補完しているからでそう思うのである。
「日本人以外の集合なのだから、ゴキブリの集合だって日本人以外の集合じゃんね。そもそもゴキブリは人じゃないし。」とも言える。
このように、「〇〇の範囲で」という範囲指定が無いと”以外の”という集合はとてつもなく広くなってしまい、むしろ考察する意味がなくなってしまう。
したがって、「ある範囲の中で△△以外の□□」という範囲指定がなされた差集合を考える必要があるのである。
最も、「ある範囲」が明らかな場合(例えば整数の話をしているとき、\(6\)の倍数でない集合と言われたら「\(6\)で割り切れない整数の(←これが範囲)集合だよね」のようなとき)は「ある範囲」が省略されて書かれることもある。
直積集合
集合において、”和”と”差”に対応する集合がある、ということを上記で述べた。
実は、”積”、”商”に対応する集合もある。
ただし、”商”に対応する集合については二項関係という概念を説明せねばならないので、本記事では省く。(次回)
一言だけ言っておくと”商”に対応する集合(商集合という)はある集合をカテゴリーに”分ける”ときに使われ、その各カテゴリーの名前の集合である。(ふーん、くらいでいいです。)
“積”に対応する、といっても掛け算をする、というわけではない。
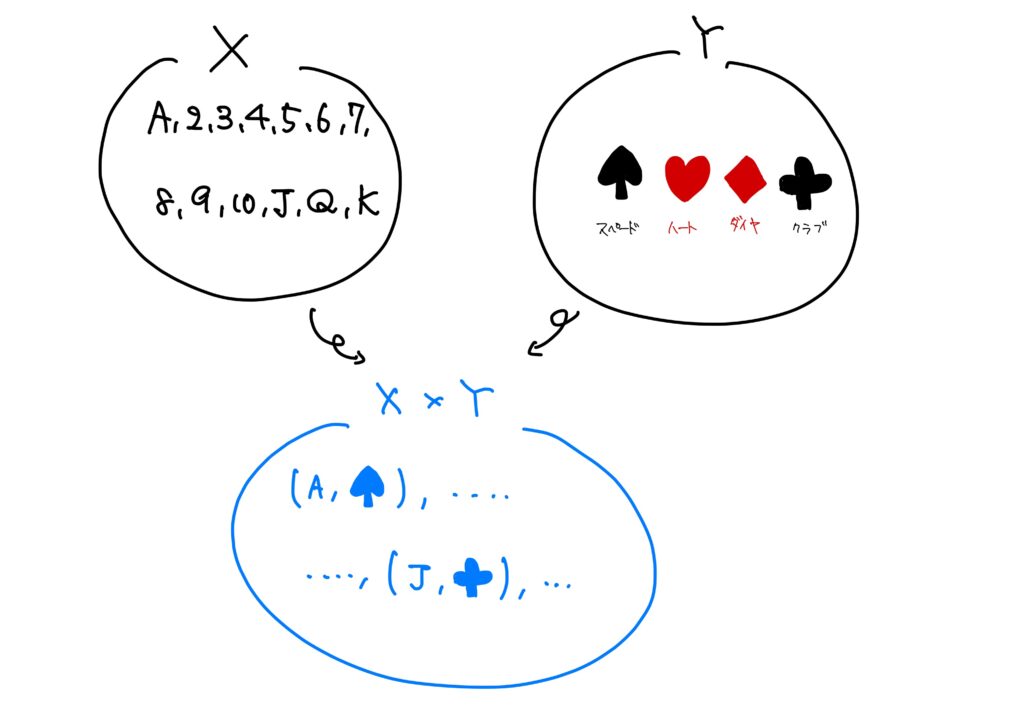
例えば、トランプ(元大統領ではない)を考えてみよう。
Jokerを除いたトランプは52枚1組で、その内訳はA,2,3,4,5,6,7,8,9,10,J,Q,Kの数字と♠、♥、◆、♣との組み合わせである。
つまり、♣の\(7\)というカードは\(7\)という数字と♣というマークの組として捉えることができる、というわけである。
これを集合の言葉を使って表してみると、
\(\{A,2,3,4,5,6,7,8,9,10,J,Q,K\}\)と\(\{♠、♥、◆、♣\}\)の集合からそれぞれ1つずつ要素を選んで、その組が1枚のカードである、というわけである。
一般に、\(x\)と\(y\)の組を\((x,y)\)と書く。
この気泡に従えば、♣の\(7\)というカードは数字の\(7\)と♣の組であるから、\((7,♣)\)と書ける。
従って、トランプは
$$トランプ=\{ (A,♠),(2,♠),\dots, (A,♥),(2,♥),\dots(A, ◆),(2,◆),\dots(A,♣),(2,♣),\dots \}$$
と書けるわけである。
このように、複数の集合の要素を1つずつ選んで、その組を要素とする集合の事を直積集合(direct product)あるいはデカルト積(Cartesian product)という。
(「一体これのどこが掛け算だというんだ」となるかもしれないが、ちょっとこらえてほしい。後述。)
豆知識
「デカルト積、って言ってるのになんでCartesian(かるてしあん)なの? Descartes productじゃないの?」と思うかもしれない。
デカルトの本名はルネ・デカルト(仏:Rene Descartes)なのだが、ラテン語ではレナトゥス・カルテシウス(Renatus Cartesius)という。
このラテン語名からCartesian productが来ている。
ちなみに、デカルト座標系もCartesian coordinateという。
さて、直積集合ってどんな集合?というと、
$$集合Xと集合Yからそれぞれ1つずつ選んできた要素の組を要素とする集合$$
である。
これを論理式で書けば、
上記の記号を用いてトランプを表すと、
- \(X\):\(\{x\in\mathbb{N}\mid 2\leq x\leq10\}\cup\{A,J,Q,K\}=\{A,2,3,4,5,6,7,8,9,10,J,Q,K\}\)
- \(Y\):\(\{♠、♥、◆、♣\}\)
としたとき、\(トランプ=X\times Y\)である。
直積集合のよく使われる例として、「座標」がある。
2次元の場合、今まで何の気無しに\(x\)軸と\(y\)軸を描いて、クラフを描いて、図形を描いて、としてきたかもしれないが、その座標というのは「実数と実数の組」なのである。
すなわち、2次元の実数の座標は\(\mathbb{R}\times\mathbb{R}\)の要素である、と捉えることができる、ということである。
このとき\(\mathbb{R}\times\mathbb{R}\)を\(\mathbb{R}^2\)と書く。
また、3次元の場合は\(\mathbb{R}^3\)と書く。
同様にして、\(n\)次元の場合の座標は\(\mathbb{R}\times \mathbb{R}\times \dots \times \mathbb{R}\)の要素として捉えることができ、これを\(\mathbb{R}^n\)と書く。
さて、「どこが掛け算なんだ、積なんだ」となってるかもしれない。
勿論、厳密に掛け算だというわけではない。
ただ、九九を思い出してみると\(2\times 3=6\)というのは、「\(2\)が\(3\)つあるから\(6\)だ」と捉えることもできるが、「2つの数字\(2\)と\(3\)の組に対して、\(6\)という数字が対応している」と捉えることもできる。
そういう意味で”積”なのである。
ただ、一般に\(X\times Y\)と\(Y\times X\)は等しくない。
座標\((2,3)\)と\((3,2)\)は等しくない。
勿論、先の九九のように入れ替えても等しい場合もあるが、一般には等しくない。
「直積集合は複数の集合の要素の組を要素とする集合だ」と述べた。
勿論これは正しいのだが、幾何学的な別の捉え方をすることもできる。
幾何学の分野でよく出現するドーナツ型の立体(これをトーラスという)は、単位円周の集合\(S^1=\{(x,y)\in\mathbb{R}^2\mid x^2+y^2=1\}\)の直積集合(に適当な条件を入れた集合)として書かれる。
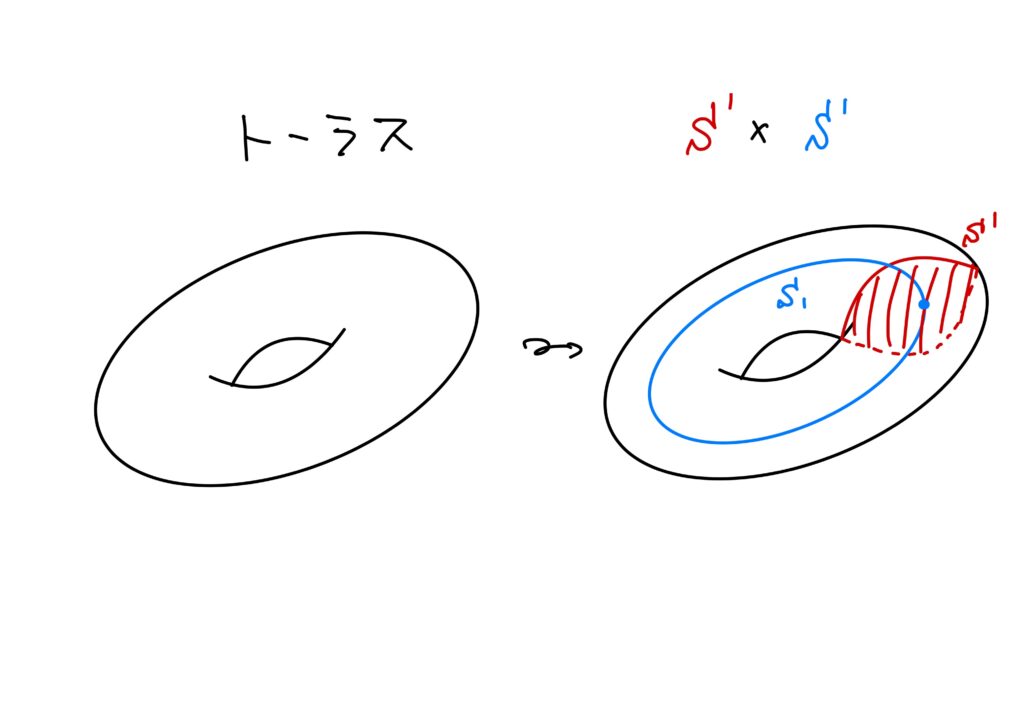
すなわち、トーラス\(T\)は\(S^1\times S^1\)に適当な条件を入れた集合というわけである。
図のように、トーラスは「単位円周が、もう一つの単位円周に沿ってぐるりと展開されている」と捉えることができる。
(とはいえ少々言葉では難しいので、次回の集合族の記事でもう少し詳しく述べます。)
要は、直積集合は幾何学的に捉えることもできますよ、ということである。
結
今回は「ベン図」、「和集合」、「共通部分」、「差集合」、「補集合」、「直積集合」について解説した。
ベン図は複数の集合の関係性を視覚的に理解するための図である。
しかしながら、なにか命題を証明する場合、ベン図は根拠にはなりえない、ということに注意する。
和集合は複数の集合を”合わせた”集合であり、四則演算における”和”に対応する集合である。
共通部分は複数の集合に”共通した部分の集合”である。
つまり共通部分は複数の集合に対して同時に部分集合となるような集合なのである。
差集合はある集合からある集合を”取り除いた部分”の集合であり、四則演算における”差”に対応する集合である。
補集合は、ある範囲の中で、その範囲の集合”でない部分”の集合である。
直積集合は複数の集合の要素の組を要素とする集合であり、四則演算における”積”に対応する集合である。
勿論、四則演算における”商”に対応する「商集合」もある。これについては次回解説する。
これらの集合は数学の世界では頻繁に使われるため、ぜひ覚えてほしいところである。
今回の記事が少々長くなってしまったため、次回は当初の予定を変更して、「ベキ集合」、「二項関係、特に同値関係」、「商集合」、「集合族」について解説する。
となるわけである。
これらの集合や概念も本記事の内容と同じくらいよく出現する。
そして、いよいよ次次回は実数の連続性について解説する。
質問などございましたらドシドシコメントを下さい!
乞うご期待!



コメントをする