「写像って？」「関数？」「合成写像って？」【論理と集合シリーズ】写像編まとめ①

本記事の内容
序
「写像…?何すか写像って？」
1. 写像と関数はほとんど同じもの
2. 「なんだろう。もうちょっと詳しく教えてもらってもいいすか？」
写像ってどんなの？
で、何すか写像って？
え？結局のところ写像って関数なんじゃね？
写像$f:X\to Y$に付随する概念の名称
1. 定義域、終域
2. 順像および逆像
2つの写像が等しいって？
合成写像
結

本記事の内容

本記事は「写像って何？」とうことを皮切りに、特別な性質を持つ写像についての初歩を解説する記事である。
写像は関数の極限を語る上で避けては通れない概念である。
この記事を読むに当たり、論理と集合の初歩を知っている必要があるため、そこに不安がある方は以下の記事を参照してください。
※シリーズ化しているため、その一部を掲載しています。

序

【論理と集合シリーズ】と銘打っているものの、写像は集合とセットにして語られることが多い。
なぜならば、写像は2つの集合に対しての概念だからである。

論理と集合シリーズの最初の方で、「現代数学は集合の言葉で書かれている。」という趣旨のことを説明したのだが、実はこれは正確ではない。
正直なところ、「現代数学は集合と写像の言葉で書かれている。」が正しい。
故に、集合と写像は数学における言語なのであって、言語がわからないと文章が読めないのだから基本の「き」である。

基本の「き」であるにも関わらず、いざ写像を語ろうとすると少々抵抗があるのが実情と思われる。
(何度も何度も本を読み込み、触れる機会を多くすれば慣れるのだが、そういう経験は大事である一方時間がかかってしまう。)
この抵抗感は高校数学までの知識や感覚を一般化した(より広く抽象的に述べた)概念なので、それらと少々乖離しているからであると思われる。

これは筆者の感覚なのだが、写像についてしっかり理解している大学生は実は少ないのではないか、と思っている。
というのも、概念自体が抽象的なだけでなく、多くの参考書やら専門書での解説も抽象的だからである。
その上、写像をしっかり理解していなくとも、計算ができてしまう、ということもまた背景の一つだと思う。
ある種、直感的な理解で計算自体はできてしまう、ということである。

しかし、いざ厳密に数学を考えよう、と思ったらばそうもいかない。
「これはどこからどこへの写像でどういうことを満たすんだろうか？」ということがわからなければ、命題の真意を汲み取ることはできない。
「事実として知っておきたい！」というだけなのであれば、これで十分なのだが、それは理解ではなくあくまで”知っている”に過ぎないと思う(と、少々キツイことを言ってみる。筆者も耳が痛いんだよね。)。

「写像…?何すか写像って？」

このセリフは皆さんご存知だと思われる。
(ご存知ない方はぜひ一度ググってみるとすぐ出てきます。結構面白いです。)
このセリフは某論破王が投げかけたものだが、それよりも評論家の方が「写像」という言葉を知っている事に筆者は驚いた。

そんなことはさておいて、「写像…？何すか写像って？」というセリフに出てくる写像とこれから解説する写像は似て非なるものであるということをここに述べておく。

写像と関数はほとんど同じもの

早速ネタバラシしておくと、「写像…？何すか写像って？」という問いかけには「数学においてはほぼ関数と同じものです。」と答えることができる。
「”ほぼ”ってどういうことよ？」という話なのだが、数学において”関数”と言ったらば「何か数値に対して、とある新たな数値を対応付けるときの規則」という意味で使うことが多い。
この概念の本質は「ある対象に対して、別の対象(同じ場合もある)と対応付けする規則」が写像なのである。
故に、数値同士にだけでなく、数値とモノ、モノとモノの対応規則もありうる。
従って、”ほぼ”同じもの、なのである。

言うなれば「関数は数値を対象とした対応規則。写像は数値だけでなくモノをも対象とした対応規則。」ということである。
しかし、これは立場の一つに過ぎない。
専門書によっては「写像＝関数」と説明している書籍もある。
要は「写像＝関数と捉えても良いし、関数をより広くしたモノが写像であると捉えても良い。」というわけである。
本記事では後者、すなわち「写像と関数は”ほぼ”同じモノだけれども扱う対象によって、写像か関数かを呼び分けますよ。」という立場を取る。
例えば、大雑把に言えば「$f(x)=x^2$」と言われたらば「この$f$は関数だね。」といい、「$f(カレー)=スプーン$」と言われたらば「この$f$は写像だね。」ということにする。
※何だこの記号は!となるかもしれないが、後述する。

「んー。なんかしっくりこないな。」という方は「関数と写像は同じモノ」という立場を取ってもらっても構わない。
いずれの立場を取ったとしても変わらない事実は

関数は写像である。

ということだ。

「なんだろう。もうちょっと詳しく教えてもらってもいいすか？」

(某論破王の影響を受け過ぎな気もするよね。と心の中でつぶやく。)

今、写像とは「ある対象に対して、別の対象とを対応付けする規則」と述べた。
これを少々厳密に言えば、写像と2つの集合の要素に対する対応関係であるということである。
ただし、これだけでは写像とは言えず、他にも条件があるのだが、例を述べたあとに言及する。

余談その1(筆者の体験談なので読み飛ばしてOK)

実は、数学において立場が別れるという状況は写像にのみおこることではない。
筆者が知っている場合としては自然数に対する立場である。
自然数は素朴に言えば「モノを数えるときに使う数です。」である。
この自然数に「$0$を入れるか、入れないか」で立場が変わる。
例えば、皿の上にリンゴが2個あったとする。
このとき「皿の上にリンゴは何個ありますか？」といわれたらば、もちろん「2個です。」と答える。
一方で皿の上に何も乗っていないときに「皿の上にリンゴは何個ありますか？」と言われたらどうだろうか。
「リンゴはありません。」と答えたくなるのではないか。
しかし、「$0$個です。」と答えたとしても筋は通っている。
したがって、$0$を入れる立場が存在するわけである。
筆者が数論の問題について講演(といえるほど大それたものではなかったが)したときは「オノさんが言っている自然数というのは$0$は入ってますか？」と質問が来た。
「んなもん、入ってるわけねえだろうが。見りゃ分かんだろ。」と思いながら「いえ、入っていません。自然数と行ったら正の整数のことです。」と述べておいた。
$0$を自然数として捉える人もやはりいるのだなあ、と思った瞬間だった。
今更ながら、本記事、本シリーズ、というより私が書く記事すべてにおいて、自然数に$0$は含まない立場で語っている。

写像ってどんなの？

先に「ある対象に対して、別の対象(同じ場合もある)と対応付けする規則」が写像である、と述べた。
写像の例をいくつか挙げてみる。

例1.(料理を食べるときに使う食器との対応規則)
$X=\{カレー,ステーキ、おにぎり,チャーハン\}$、$Y=\{スプーン,ナイフ,手,足\}$とする。
このとき、カレーはスプーンで食べるため(手で食べる人もいるだろうが、日本人では極めて稀だと思うので排除している)、カレーとスプーンを対応させる。
同様にステーキはスプーンでは食べず、手で食べると熱い。
同様に足で食べる人もいない(見たことがない)。
ステーキはかじりつくのではなくナイフで切って小分けにして食べる。
故にステーキはナイフと対応させる。
おにぎりを食べるときにスプーン、ナイフ、足を使うことはないだろう(お上品な方は使うかもしれないが、筆者のような庶民には無縁)。
従って、おにぎりと手を対応させる。
チャーハンも同様にスプーンで食べるので、チャーハンとスプーンを対応させる。
この対応規則を$h$と書くとき、今述べた

カレーとスプーン
ステーキとナイフ
おにぎりと手
チャーハンとスプーン

という対応関係は、

$h(カレー)=スプーン$、
$h(ステーキ)=ナイフ$、
$h(おにぎり)=手$、
$h(チャーハン)=スプーン$

と書く。
すなわち、$h(対応させたいモノ)=対応するモノ$というわけである。
ここで3つ注意がある。

$X$の要素に対して、対応するモノがただ１つに定まっていること。
$X$の要素は全て使われていること。
$Y$の要素はすべて使われている必要はない、ということ。

さらに、この例の特徴を述べておくと、

$X$の別々の要素に対して、同じ$Y$の要素と対応しているものがある。

この対応規則$h$は$X$から$Y$への写像であるといい、$h:X\to Y$やら$X\stackrel{h}{\to}Y$と書く。

例2.(数学っぽい例)
$X=\{1,2,3\}$、$Y=\{1,4,9\}$とする。
$X$の要素$1,2,3$に対して$Y$の要素$1,4,9$を次のように対応させる。

$1\in X$と$1\in Y$、
$2\in X$と$4\in Y$、
$3\in X$と$9\in Y$。

この対応規則を$g$と書く。
このとき、例1.の記法に則れば、

$g(1)=1$、
$g(2)=4$、
$g(3)=9$。

である。
この例においても、

$X$の要素に対して、対応するモノがただ１つに定まっていること。
$X$の要素は全て使われていること。
$Y$の要素はすべて使われている必要はない、ということ。(今回は全て使われている。)

を満たしている。
この対応規則$g$は$X$から$Y$への写像(この場合は関数と言っても良い)であり、$g:X\to Y$やら$X\stackrel{g}{\to}Y$と書く。

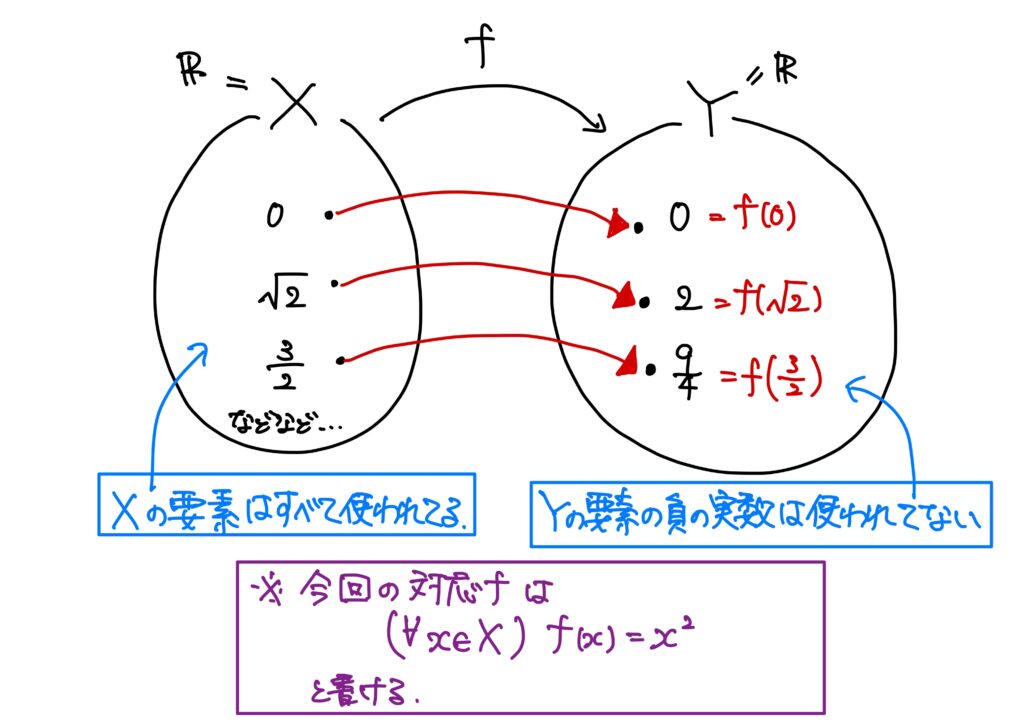
例3.(実数値の関数)
$X=Y=\mathbb{R}$とする。
このとき、任意の$x\in X=\mathbb{R}$に対して、$Y=\mathbb{R}$の要素$y$と$x^2$とを対応させる。
すなわち、任意の$x\in X$に対して、$y\in Y$を$y=x^2$で対応させる、と言っているわけである。
この記法は中学数学でも出現するため見慣れていると思われる。

例1.および例2.の記法に則れば、この対応規則$f$は
$$(\forall x\in X)\ f(x)=x^2$$
ということである。

この例においても、

$X$の要素に対して、対応するモノがただ１つに定まっていること。
$X$の要素は全て使われていること。
$Y$の要素はすべて使われている必要はない、ということ。(今回は全て使われてはいない。$Y$の要素の負の実数には対応する$X$の要素がない。)

を満たしている。
この対応規則$f$は$X=\mathbb{R}$から$Y=\mathbb{R}$への写像であり、数に対しての対応規則なので関数と呼ぶ。
このとき、$f:\mathbb{R}\to\mathbb{R}$やら$\mathbb{R}\stackrel{f}{\to}\mathbb{R}$と書く。

この記法$f(x)=x^2$は高校数学で出現している。
この記法の意味は$x\in\mathbb{R}$に対して、$x^2\in\mathbb{R}$を対応させる規則が$f$ですよ、ということだったのだ。

で、何すか写像って？

というわけで、今まで述べた写像の正体を素朴に述べる。

写像(素朴ver.)
$X$と$Y$を集合とする。$f$が$X$から$Y$の写像であるとは、$X$の任意の要素$x$に対して、$Y$の要素$y$がただ一つ定まることをいう。このとき、$y=f(x)$と書く $f$が$X$から$Y$への写像であることを$f:X\to Y$やら$X\stackrel{f}{\to}Y$と書く。また、$f$により$x$が$y$に対応することを$f:x\mapsto y$とも表す。これは、$y=f(x)$と同じ意味である。

つまり、任意の$X$の要素に対して、その対応先を指定することで写像が決まる、というわけだ。

さて、先に述べた通り、これ素朴な写像の説明である。
これだと「ん？」となるかもしれない。
というのも、先は
「$f$が$X$から$Y$への写像である。」ことを「$X$の任意の要素$x$に対して$Y$の要素$y$がただ一つ定まる。」ことという説明だからである。
すなわち、$f$が$X$から$Y$への写像であるという状態は、任意の$X$の要素$x$に対して$Y$の要素$y$がただ一つ定まっている状態である、という説明である。
くどいかもしれないが、これでは「写像である、という状態」は説明しているのだが、写像とは何か？という問には答えられていない。
例えば、「奇数って何すか？」と言われたらば、「$2$で割って$1$あまる整数。」と答えるのだが、奇数の正体は「整数」である。
この例における「整数」に対応するものが上記の写像の説明にはない。

しかし一方で、上記の説明は正しいのもまた事実である。
つまり、「$X$の任意の要素$x$に対して、$Y$の要素$y$がただ一つ定まっている状態のとき、$f$は$X$から$Y$への写像であると呼ぶ。」のだから、この$f$が写像である、と言いかえることができるからである。

例1.,2.,3.,を再度見直してみよう。

例1.(料理を食べるときに使う食器との対応規則)
$X=\{カレー,ステーキ、おにぎり,チャーハン\}$、$Y=\{スプーン,ナイフ,手,足\}$とする。
このとき、

カレーとスプーン
ステーキとナイフ
おにぎりと手
チャーハンとスプーン

という対応$h$を考える。
このとき、任意の$x\in X$($x$の正体はカレー、ステーキ、おにぎり、チャーハン)に対して、$y\in Y$($y$の正体はスプーンで、ナイフ、手、足)がただ一つ定まっているため、

$スプーン=h(カレー)$、
$ナイフ=h(ステーキ)$、
$手=h(おにぎり)$
$スプーン=h(チャーハン)$

と書くことができる。
従って、この対応$h$は$X$から$Y$への写像であり、$h:X\to Y$やら$X\stackrel{h}{\to}Y$と書く。

例2.(数学っぽい例)
$X=\{1,2,3\}$、$Y=\{1,4,9\}$とする。
$X$の要素$1,2,3$に対して$Y$の要素$1,4,9$を次のように対応させる。

$1\in X$と$1\in Y$、
$2\in X$と$4\in Y$、
$3\in X$と$9\in Y$。

この対応$g$を考える。
このとき、任意の$x\in X$($x$の正体は$1,2,3$)に対して、$y\in Y$($y$の正体は$1,4,9$)がただ一つ定まっているため、

$g(1)=1$、
$g(2)=4$、
$g(3)=9$。

と書く事ができる。
従って、この対応$g$は$X$から$Y$への写像(この場合は関数と言っても良い)であり、$g:X\to Y$やら$X\stackrel{g}{\to}Y$と書く。

例3.(実数値の関数)
$X=Y=\mathbb{R}$とする。
このとき、任意の$x\in X=\mathbb{R}$に対して、$Y=\mathbb{R}$の要素$y$と$x^2$とを対応させるような対応$f$を考える。
このとき、任意の$x\in X$($x$の正体は実数)に対して、$y\in Y$($y$の正体は実数)がただ一つ定まっているため、

$f(1)=1$、
$\displaystyle f\left(\frac{3}{2}\right)=\frac{9}{4}$、
$f(7)=49$、
$f(\sqrt{2})=2$
などなど…

と書く事ができる。
従って、この対応$f$は$X$から$Y$への写像(この場合は関数と言っても良い)であり、$f:X\to Y$やら$X\stackrel{f}{\to}Y$と書く。

写像(素朴ver.)を見て「なるほどね」となったらば、それでOKである。
しかし、「なんか納得できねえな。対応ってなんだ。」となっている方は次の集合の言葉を使った説明を読むと一手に解決されると思われる。

写像(集合の言葉ver.)
2つの空でない集合$X$、$Y$の直積集合$X\times Y$の部分集合$f$が次の2条件を満たすとき、$f$を$X$から$Y$への写像(the map from $X$ to $Y$)と呼ぶ。

$(\forall x\in X)(\exists y\in Y)\ {\rm s.t.}\ (x,y)\in f$.
$(\forall (x_1,y_1)\in f)(\forall (x_2,y_2)\in f)\ x_1=x_2\Rightarrow y_1=y_2$.

ここで注意なのが、

$X$の要素全てに対して、$Y$の要素がただ１つ定まっている。

ということである。
$X$の要素の中に$Y$の要素と対応しない要素があれば、その対応$f$は写像ではない。

さて、$X$から$Y$への写像$f$の正体はなにか、というと、

$X\times Y$の部分集合だ！

ということである。
くどいかもしれないが、再度例1.,2.,3.,を見てみよう。

例1.(料理を食べるときに使う食器との対応規則)
$X=\{カレー,ステーキ、おにぎり,チャーハン\}$、$Y=\{スプーン,ナイフ,手,足\}$とすると、
$$X\times Y=\{(カレー,スプーン),(カレー,ナイフ),(カレー,手),(カレー,足),\\ \
(ステーキ,スプーン),(ステーキ,ナイフ),(ステーキ,手),(ステーキ,足),\\ \
(おにぎり,スプーン),(おにぎり,ナイフ),(おにぎり,手),(おにぎり,足),\\ \
(チャーハン,スプーン),(チャーハン,ナイフ),(チャーハン,手),(チャーハン,足),\}$$
である。
このとき、
$$h=\{(カレー,スプーン),(ステーキ,ナイフ),(おにぎり,手),(チャーハン,スプーン)\}$$
とすれば、$h\subset X\times Y$であり、任意の$x\in X$($x$の正体はカレー、ステーキ、おにぎり、チャーハン)に対して、$y\in Y$($y$の正体はスプーン、ナイフ、手、足)が存在して、$(x,y)\in h$である。
実際、

カレー$\in X$に対して、スプーン$\in Y$が存在して、$(カレー,スプーン)\in h$,
ステーキ$\in X$に対して、ナイフ$\in Y$が存在して、$(ステーキ,ナイフ)\in h$,
おにぎり$\in X$に対して、手$\in Y$が存在して、$(おにぎり,手)\in h$,
チャーハン$\in X$に対して、スプーン$\in Y$が存在して、$(チャーハン,スプーン)\in h$.

であるからである。
さらに、$(\forall (x_1,y_1)\in h)(\forall (x_2,y_2)\in h)\ (x_1=x_2\Rightarrow y_1=y_2)$も満たしている。
特に、この命題の対偶$(\forall (x_1,y_1)\in h)(\forall (x_2,y_2)\in h)\ (y_1\neq y_2\Rightarrow x_1\neq x_2)$を満たしている。
実際、

(カレー,スプーン)$\in h$と(ステーキ,ナイフ)$\in h$を$h$から任意に選んだとき、カレー$\neq$ステーキである。
(カレー,スプーン)$\in h$と(おにぎり,手)$\in h$を$h$から任意に選んだとき、カレー$\neq$おにぎりである。
(ステーキ,ナイフ)$\in h$と(おにぎり,手)$\in h$を$h$から任意に選んだとき、ステーキ$\neq$おにぎりである。
(ステーキ,ナイフ)$\in h$と(チャーハン,スプーン)$\in h$を$h$から任意に選んだとき、ステーキ$\neq$チャーハンである。
(おにぎり,手)$\in f$と(チャーハン,スプーン)$\in h$を$h$から任意に選んだとき、おにぎり$\neq$チャーハンである。

従って、この対応$h$は$X$から$Y$への写像である。$h:X\to Y$やら$X\stackrel{h}{\to}Y$と書き、$h(カレー)=スプーン、h(ステーキ)=ナイフ、h(おにぎり)=手、h(チャーハン)=スプーン$と書く。

例2.(数学っぽい例)
$X=\{1,2,3\}$、$Y=\{1,4,9\}$とすると、
$$X\times Y=\{(1,1),(1,4),(1,9),\
(2,1),(2,4),(2,9),\
(3,1),(3,4),(3,9),\}$$
である。
このとき、
$$g=\{(1,1),(2,4),(3,9)\}$$
とすれば、$g\subset X\times Y$であり、任意の$x\in X$に対して、$y\in Y$が存在して、$(x,y)\in g$である。
実際、

$1\in X$に対して、$1\in Y$が存在して、$(1,1)\in g$,
$2\in X$に対して、$4\in Y$が存在して、$(2,4)\in g$,
$3\in X$に対して、$9\in Y$が存在して、$(3,9)\in g$,

$(1,1)\in g$と$(2,4)\in g$を$g$から任意に選んだとき、$1\neq2$である。
$(1,1)\in g$と$(3,9)\in g$を$g$から任意に選んだとき、$1\neq3$である。
$(2,4)\in g$と$(3,9)\in g$を$g$から任意に選んだとき、$2\neq3$である。

従って、この対応$g$は$X$から$Y$への写像であり、$g:X\to Y$やら$X\stackrel{g}{\to}Y$と書き、$g(1)=1、g(2)=4、g(3)=9$と書く。

例3.(実数値の関数)
$X=Y=\mathbb{R}$とすると、$X\times Y=\mathbb{R}\times\mathbb{R}=\mathbb{R}^2$である。
このとき、
$$f=\{(x,x^2)\mid x\in X\}$$
とすれば、$f\subset X\times Y$であり、任意の$x\in X$に対して、$y\in Y$が存在して、$(x,y)\in f$である。
実際、任意の実数$x$に対して、それを二乗した数$x^2$もまた実数であり、$x^2$という値は必ず1つである。
(※例えば自然数$7$に対して、その二乗した数は$49$であり、$49$以外の数にはなりえない。これがすべての実数で成り立つ。)

さらに、$(\forall (x_1,y_1)\in f)(\forall (x_2,y_2)\in f)\ (x_1=x_2\Rightarrow y_1=y_2)$も満たしている。
実際、任意の$(x_1,y_1)\in f$と任意の$(x_2,y_2)\in f$に対して、$y_1=x_1^2$かつ$y_2=x_2^2$を満たしているので、$(x_1,y_1)=(x_1,x_1^2)$かつ$(x_2,y_2)=(x_2,x_2^2)$である。
今、$x_1=x_2$なのだから、$x_1^2=x_2^2$であるので、$y_1=y_2$である。

従って、この対応$f$は$X$から$Y$への写像であり、$f:X\to Y$やら$X\stackrel{f}{\to}Y$と書き、任意の$x\in X$に対して$(x,y)\in f$となる$y\in Y$を$y=f(x)$と書く。
すなわち、$x^2=f(x)$と書く。

え？結局のところ写像って関数なんじゃね？

序盤でも述べたとおり、概ねそのとおりである。
上記の3つの例は関数色が強い例を挙げたからである。
そこで、関数というより写像っぽい(と筆者が思う)例を挙げる。

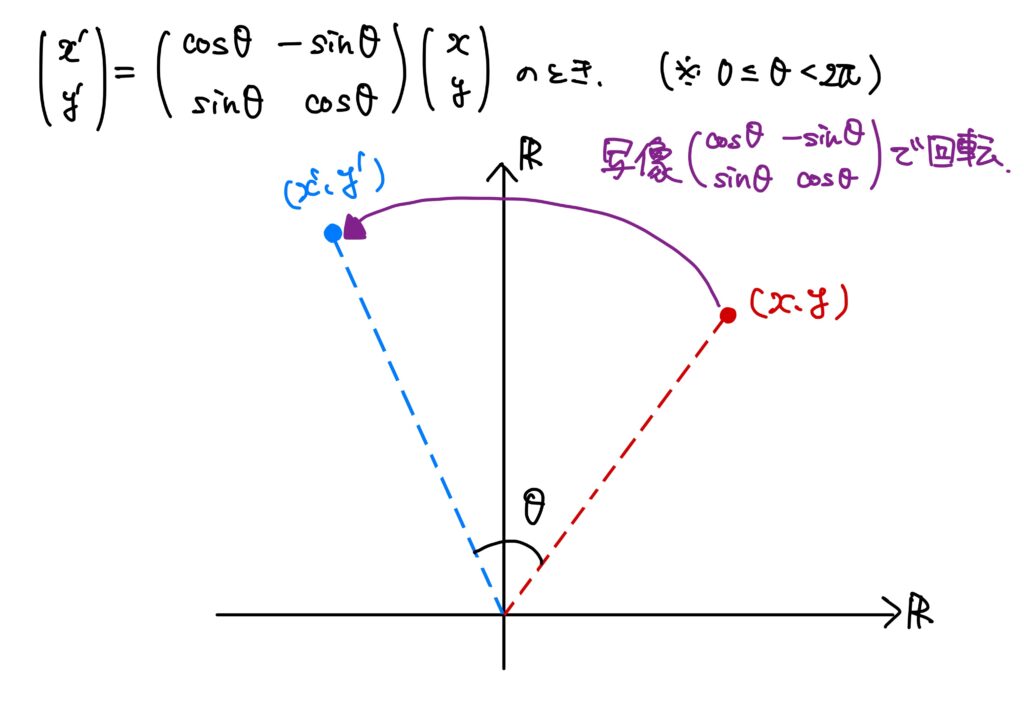
例4.($\mathbb{R}$の一次変換)
$a,b,c,d\in\mathbb{R}$とする。
写像$f:\mathbb{R^2}\to\mathbb{R}^2$を以下のように定める。
$(x’,y’)=f(x,y)$として、
$$
\begin{pmatrix}
x’\\
y’
\end{pmatrix}=
\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}
\begin{pmatrix}
x\\
y
\end{pmatrix}
$$
とする。
これは、$ad-bc\neq0$のとき、$(x,y)$が直線上の点であれば、$(x’,y’)$は別の直線上の点である。
要は、$ad-bc\neq0$のとき、直線は直線に、線分は線分に、三角形は三角形に、平面全体は平面全体に写す。
すなわち、ある点を別の点に写す(移動する)という写像である。

写像$f:X\to Y$に付随する概念の名称

定義域、終域

呼び名(全部ではありません。)
$f:X\to Y$を写像とする。

$f(x)$を$f$による$x$の像(the image of $x$ under $f$)、$f$の$x$における値(the mapping value at $x$)という。
$X$を写像$f$の定義域(the domain of $f$, the domain of definition of $f$)という。他に、始域、始集合と呼ぶこともある。
$Y$を写像$f$の終域とよぶ。

順像および逆像

例1.について、$X=\{カレー,ステーキ,おにぎり,チャーハン\}$、$Y=\{スプーン,ナイフ,手,足\}$であった。
このとき、$h:X\to Y$は

$h(カレー)=スプーン$、
$h(ステーキ)=ナイフ$、
$h(おにぎり)=手$、
$h(チャーハン)=スプーン$

としたのだった。
これは、集合$X$の任意の要素が集合$Y$の部分集合$\{スプーン,ナイフ,手\}$の要素と対応がある、と捉えることができる。
更にいえば、$X$の部分集合$\{カレー,おにぎり\}$の任意の要素が集合$Y$の部分集合$\{スプーン,手\}$の要素と対応がある、というように部分集合の対応先も考えることができる。
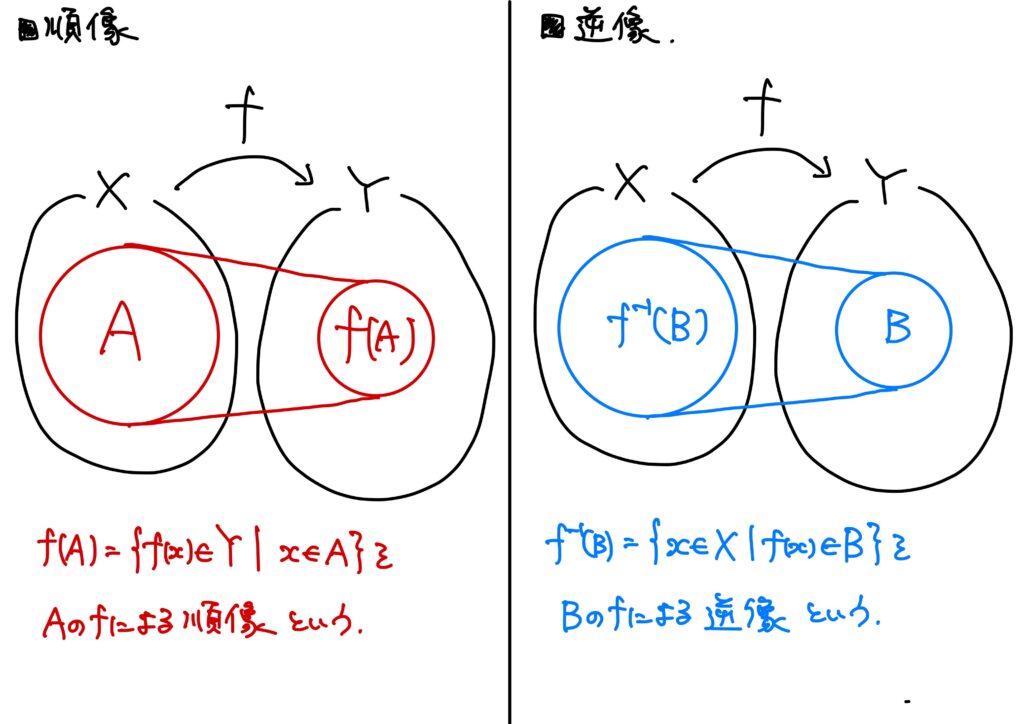
このように、$X$の部分集合$A$の任意の要素$a\in A\subset X$と対応する$y\in Y$の要素の集合を順像(the image of $A$ under $f$)という。
特に、$A=X$である場合、すなわち、任意の$x\in X$に対して、それらと対応する$y\in Y$の要素の集合は値域(the range of $f$)という。
言ってしまえば、順像は$x\in X$のときの$f(x)$を要素とする集合だ、というわけである。

ちなみに、高校数学で学ぶであろう関数の値域は、関数を写像とみなしたとき、ここで言うところの値域なのである。

一方で、順像とは逆の集合もある。
$Y$の要素と対応する$X$の要素の集合、ということである。
$Y$の部分集合$\{ナイフと手\}$の要素であるナイフと手はそれぞれ、$X$の部分集合$\{ステーキ,おにぎり\}$の要素と対応がある。
すなわち、終域の対応されている要素に対して、その一部(または全体)と対応している定義域の要素の集合を考えることもできる。
このようにこのように、$Y$の部分集合$B$の任意の要素$b\in B\subset Y$と対応する$x\in X$の要素の集合を逆像(the inverse image of $B$)という。

以上のことを記号を使って書けば、次である。

順像、逆像

順像

順像

値域

逆像

逆像

2つの写像が等しいって？

今までは1つの写像について話してきた。
一旦、複数の写像について、特に2つの写像についての諸概念を述べる。
今まで挙げた例1,2,3はどれも写像として一致しない。
「対応させるモノが違うんだからそりゃそうでしょ」と言う気もするのだが、こんな例はどうだろうか。

例4.(写像の一致)
$X=\{1,2,3\}$、$Y=\{4,5\}$とする。
これらの集合に対する写像$f:X\to Y$を$f(1)=f(2)=4$、$f(3)=5$で定める。

新たに、$g:X\to Y$を$g(x)=\max\{x+2,4\}$、すなわち、$x\in X$に対して、$x+2$と$4$のうち大きい方を$g(x)$の値として採用するとする。
すると、
$$g(1)=\max\{1+2,4\}=4,\ g(2)=\max\{2+2,4\}=4,\ g(3)=\max\{3+2,4\}=5$$
となる。
さらに、
$h:X\to Y$を$\displaystyle h(x)=\left[\frac{x+7}{2}\right]$(ただし、$[]$はGauss記号)として$h$を定めれば、
$$h(1)=\left[\frac{8}{2}\right]=4,\ h(2)=\left[\frac{9}{2}\right]=4,\ h(3)=\left[\frac{10}{2}\right]=5$$
である。

従って、対応させるための規則は$f,g,h$でそれぞれ異なっているが、対応する数は一致している。
このとき、$f,g,h$は一致する、というのが写像が等しいということである。
つまり、2つの写像に対して、対応させる規則が異なっていたとしても、定義域と終域と対応するモノが一致しているとき、それらは等しいというのだ。
これを論理式で書くと次である。

写像の相等
2つの写像$f_1:X_1\to Y_1$と$f_2:X_2\to Y_2$が等しいとは、 $$(X_1=X_2)かつ(Y_1=Y_2)かつ((\forall x\in X_1)\ f_1(x)=f_2(x))$$ が成り立つことをいう。

合成写像

とどのつまり、合成写像は高校数学で学んだ合成関数の写像ver.である。
筆者の感覚だが、合成写像は微積分の分野で活躍する概念だと思う。
というのも、一見複雑そうな関数でも、新たな変数(パラメータ)を用意してそのパラメータを経由させることで関数自体を簡素化させて理解しやすくなる場合があるからである。
ここでは述べないのだが、ニューラルネットワークの核にも合成関数が使われている。

例えば、次のような場合を考えてみる。

例5.(合成写像)

$A=$日本国民の集合,
$B=$全ての年齢からなる集合,
$C=$全ての年齢区分からなる集合$=\{0\sim14歳の区分,15\sim64歳の区分,65歳\simの区分\}$

とする。
写像$f:A\to B$を任意の日本国民$a\in A$に対して、$f(a)=a$の年齢として定める。
また、写像$g:B\to C$を任意の年齢$b\in B$に対して、$g(b)=b$が属す年齢区分として定める。
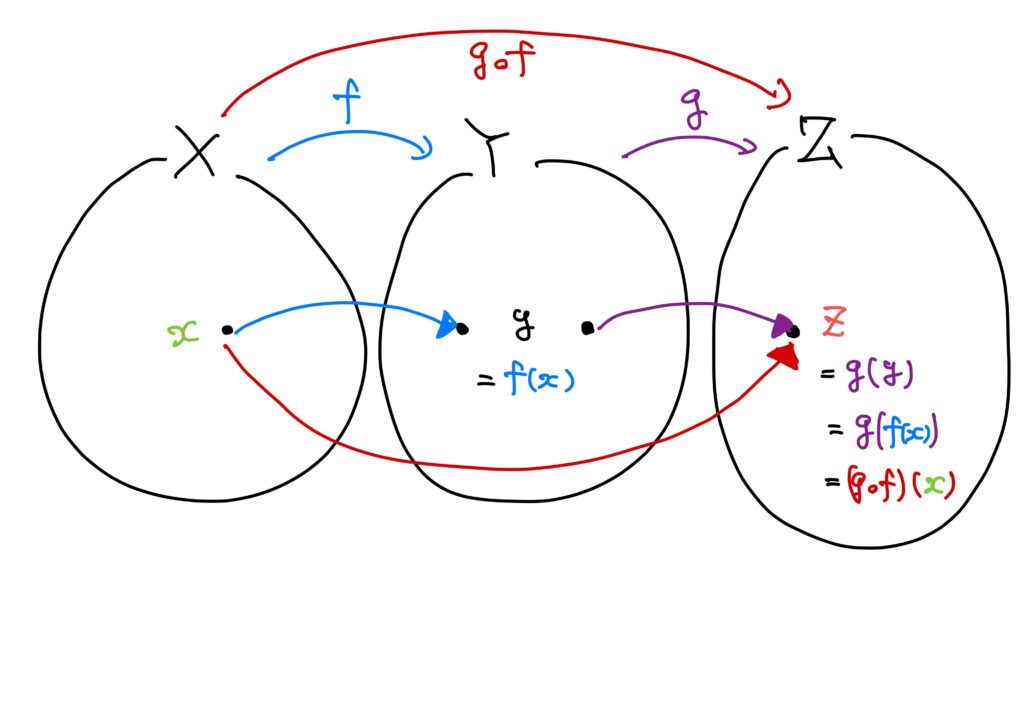
このとき、$h:A\to C$を$h(a)=g(f(a))$で定める。
すなわち、$h$は、任意の日本国民$a\in A$に対して、$a$が属する年齢区分を対応させる写像である。
※$f$も$g$も写像として定まっているのだから、$g(f(a))$も定まる。
このとき、$h$を$h=g\circ f$と書く。
つまり、$h(a)=(g\circ f)(x)=g(f(a))$である。
この$h$のこと、すなわち$g\circ f$のことを$f$と$g$の合成写像という。
実際に展開してみると、
\begin{eqnarray}
h(a)&=&(g\circ f)(a)\\
&=&g(f(a))\\
&=&g(aの年齢)\\
&=&aの年齢が属する年齢区分\\
&=&aが属する年齢区分
\end{eqnarray}
となる。

例6.(合成関数)

$X=\mathbb{R}$,
$Y=[-1,1]$,
$Z=\mathbb{R}$

とし、

$f:X\to Y$を任意の$x\in X$に対して、$f(x)=\sin x$,
$g:Y\to Z$を任意の$y\in Y$に対して、$g(y)=2^y$,

とする。
このとき、$g\circ f:X\to Z$を$(g\circ f)(x)=g(f(x))$で定める。
この$g\circ f$を$f$と$g$の合成写像(合成関数)という。

ここで、
\begin{eqnarray}
(g\circ f)(a)&=&g(f(x))\\
&=&g(\sin x)\\
&=&2^{\sin x}
\end{eqnarray}
である。

このように、2つの集合にもう１つの集合を加えて、その加えた集合を経由させる写像を合成写像という。
これを式で表すと次である。

合成写像(合成関数)
$f:X\to Y$、$g:Y\to Z$を写像とする。このとき、写像$h:X\to Z$を $$h(x)=g(f(x))\ (x\in X)$$ で定める。この$h$を$f$と$g$の合成(the composition of $f$ and $g$)、あるいは合成写像(the composite mapping)と呼び、$g\circ f$で表す。すなわち、$g\circ f:X\to Z$は $$(g\circ f)(x)=g(f(x))\ (x\in X)$$ で定められる写像である。また、このとき$X\xrightarrow{f}Y\xrightarrow{g}Z$、$h=g\circ f$と書くこともある。

合成写像の性質として、「定義域と終域が適切であれば、どの順番で合成しても写像は同じ」というものがある。
これを証明してみよう。

定理7.(合成写像に対する結合律)
$f:X\to Y$、$g:Y\to Z$、$h:Z\to W$を写像とする。このとき、 $$h\circ(g\circ f)=(h\circ g)\circ f$$ が成り立つ。

この定理の証明はさほど難しくないので、是非挑戦してみてほしい。
証明の流れを説明する。

(ステップ1.) $h\circ(g\circ f)$と$(h\circ g)\circ f$の定義域と終域が一致することを示す。
(ステップ2.) 任意の$x\in X$に対して、$(h\circ(g\circ f))(x)=((h\circ g)\circ f)(x)$を示す。

そもそも写像が等しいとはこの2条件を満たすことだった。
では、証明に入ろう。

(証明)
(ステップ1.)
$f:X\to Y$、$g:Y\to Z$、$h:Z\to W$を写像とする。
このとき、$g\circ f:X\to Z$であるため、$X\xrightarrow{f}Y\xrightarrow{g}Z\xrightarrow{h}W$であるから、$h\circ(g\circ f):X\to W$である。
一方、$h\circ g:Y\to W$であるため、$X\xrightarrow{f}Y\xrightarrow{g}Z\xrightarrow{h}W$であるから、$(h\circ g)\circ f:X\to W$である。
従って、$h\circ(g\circ f)$と$(h\circ g)\circ f$の定義域と終域が一致する。

(ステップ2.)
任意の$x\in X$に対して、
$$(h\circ(g\circ f))(x)=h((g\circ f)(x))=h(g(f(x)))$$
であり、かつ
$$((h\circ g)\circ f)(x)=(h\circ g)(f(x))=h(g(f(x)))$$
である。
従って、任意の$x\in X$に対して、$(h\circ(g\circ f))(x)=((h\circ g)\circ f)(x)$が成り立つ。

以上により、$h\circ(g\circ f)=(h\circ g)\circ f$が成り立つ。
(Q.E.D.)

結

今回は「写像って何？」ということを皮切りに写像が等しいこと、合成写像とは何か。ということを説明した。

一言で言えば、写像は「2つの集合の要素の間にある対応のこと」である。
さらに、高校数学までで学んだ関数のことでもある。
高校数学までは、基本的に数と数の対応という意味で関数を使っていたのだが、本来対応というものは数だけを対象とするものではない。
数以外のモノでも良いわけである。

次回は「単射、全射、全単射、逆写像」について解説する。
これは特別な性質を持つ写像のことを指す。
これらは解析学で関数を扱う際に非常に重要になってくる。

乞うご期待！質問、コメントなどお待ちしております！

この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください！
ちなみに、「集合・写像・論理ー数学の基本を学ぶ」の方が入門者にはオススメです！

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34