本記事の内容
本記事は「全単射って?」ということを解説する記事である。
この記事を読むにあたり、単射、全射を知っているとより理解しやすいと思われるので、以下の記事を参照してください。
全単射のイメージは?
全単射は単射かつ全射な写像のことを指す。
読んで字の如しというわけである。
すなわち、写像の性質の中でも強い条件の部類に入ると思われる。
「全単射だと何か嬉しいのか?」と言われれば、「”全単射であるときに限り”後述する逆写像(逆関数)が存在する」ということである。
例1,1’2,3,3’を思い出してみよう。
例1.と例1′.について
例1′.(料理を食べるときに使う食器との対応規則の改変ver.)
\(X’=\{カレー,ステーキ、おにぎり\}\)、\(Y’=\{スプーン,ナイフ,手,足\}\)とする。
このとき、カレーはスプーンで食べるため(手で食べる人もいるだろうが、日本人では極めて稀だと思うので排除している)、カレーとスプーンを対応させる。
同様にステーキはスプーンでは食べず、手で食べると熱い。
同様に足で食べる人もいない(見たことがない)。
ステーキはかじりつくのではなくナイフで切って小分けにして食べる。
故にステーキはナイフと対応させる。
おにぎりを食べるときにスプーン、ナイフ、足を使うことはないだろう(お上品な方は使うかもしれないが、筆者のような庶民には無縁)。
従って、おにぎりと手を対応させる。
この対応規則を\(h_0\)と書くとき、今述べた
- カレーとスプーン
- ステーキとナイフ
- おにぎりと手
という対応関係は、
- \(h_0(カレー)=スプーン\)、
- \(h_0(ステーキ)=ナイフ\)、
- \(h_0(おにぎり)=手\)
と書かれるのだった。
このとき、カレー、ステーキ、おにぎりはそれぞれスプーン、ナイフ、手に対応しているので、カレー、ステーキ、おにぎりは別々の\(Y\)の要素と対応している。
故に単射である。
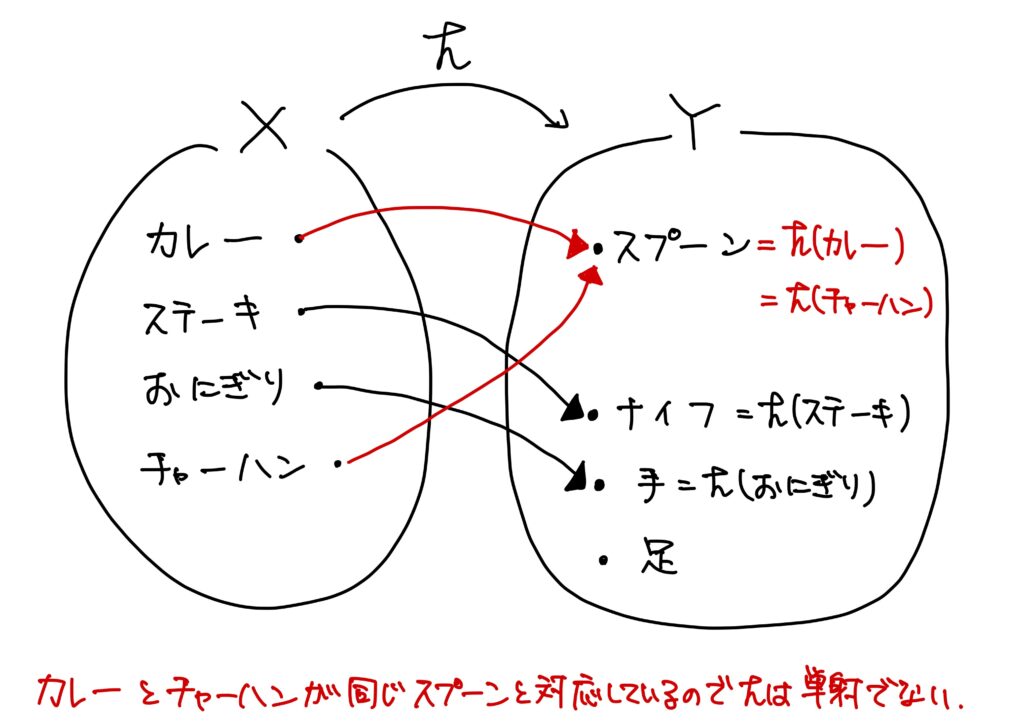
例1.は、\(X=\{カレー,ステーキ、おにぎり,チャーハン\}\)、\(Y=\{スプーン,ナイフ,手,足\}\)とし、
- カレーとスプーン
- ステーキとナイフ
- おにぎりと手
- チャーハンとスプーン
という対応だった。
つまり、
- \(h(カレー)=スプーン\)、
- \(h(ステーキ)=ナイフ\)、
- \(h(おにぎり)=手\)、
- \(h(チャーハン)=スプーン\)
だった。
この場合、カレーとチャーハンがスプーンという同じ要素に対応してしまっているので、この\(h:X\to Y\)は写像だが、単射ではない。
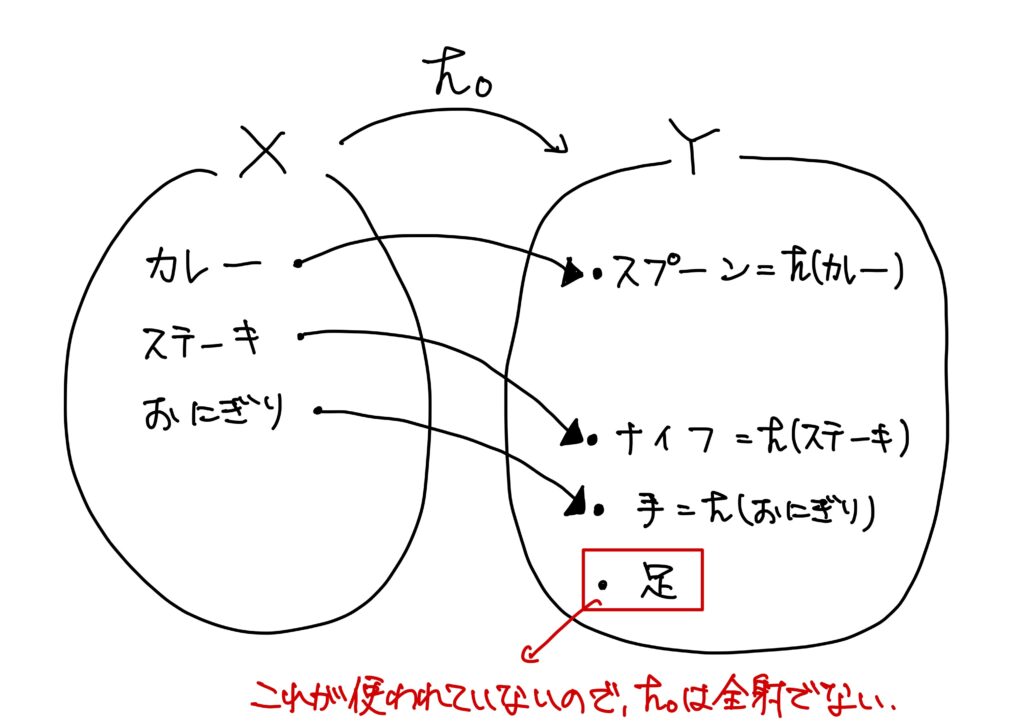
さらにこのとき、\(Y\)の要素であるスプーン、ナイフ、手にはそれぞれと対応するカレー、ステーキ、おにぎりという\(X\)の要素が存在する。
しかし、足\(\in Y\)と対応する\(X\)の要素は存在しない。
つまり、終域の要素が全て使われているわけではない(使われていない終域の要素が存在する)。
従って、この写像は全射ではない。
同様に例1.も全射ではない。
例2について
例2.(数学っぽい例)
\(X=\{1,2,3\}\)、\(Y=\{1,4,9\}\)とする。
\(X\)の要素\(1,2,3\)に対して\(Y\)の要素\(1,4,9\)を次のように対応させる。
- \(1\in X\)と\(1\in Y\)、
- \(2\in X\)と\(4\in Y\)、
- \(3\in X\)と\(9\in Y\)。
この対応規則を\(g\)と書く。
このとき、
- \(g(1)=1\)、
- \(g(2)=4\)、
- \(g(3)=9\)。
である。
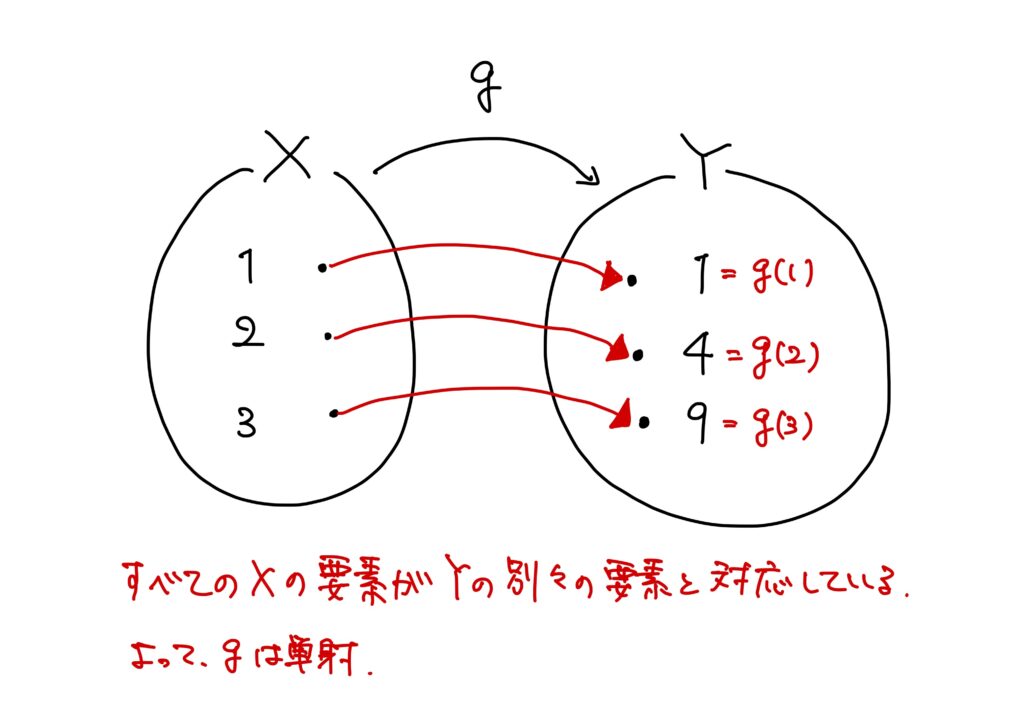
この例においても、
\(1,2,3\in X\)はそれぞれ\(1,4,9\in Y\)に対応しているので、\(1,2,3\ X\)は別々の\(Y\)の要素と対応している。
すなわち、任意の定義域の別々要素が終域の別々の要素と対応している。
従って\(g:X\to Y\)は単射である。
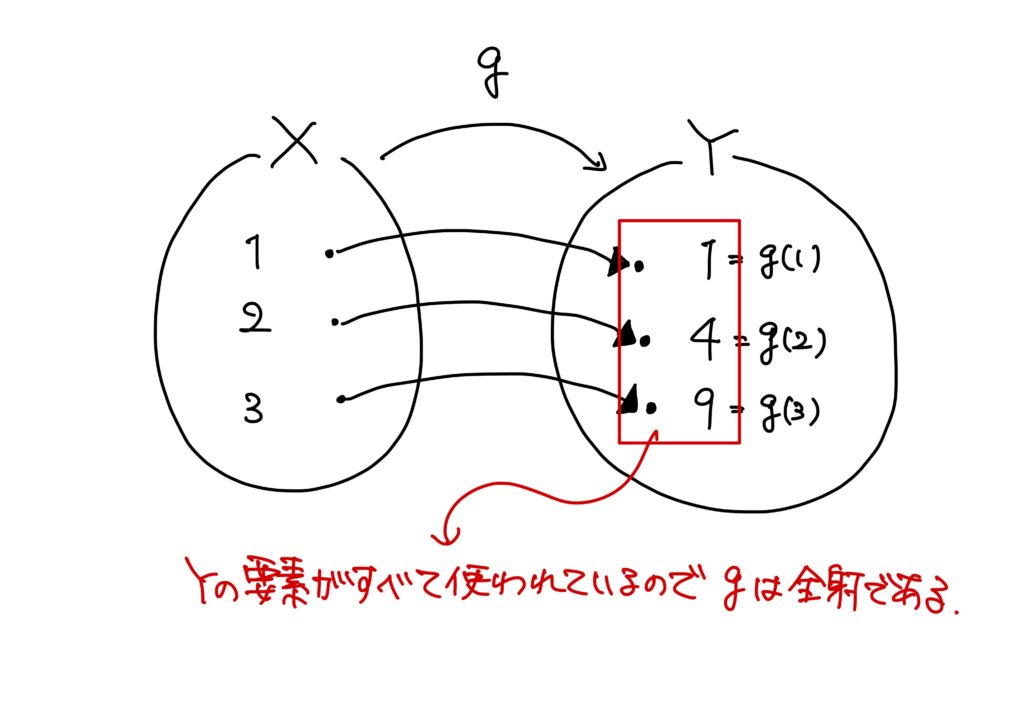
さらにこのとき、終域\(Y\)の要素\(1,4,9\)には全て、それぞれに対応する定義域\(X\)の要素が存在する。
つまり、終域のすべての要素が使われている。
従って、\(g:X\to Y\)は全射である。
例3について
例3.(実数値の関数)
\(X=Y=\mathbb{R}\)とする。
このとき、任意の\(x\in X=\mathbb{R}\)に対して、\(Y=\mathbb{R}\)の要素\(y\)と\(x^2\)とを対応させる。
すなわち、任意の\(x\in X\)に対して、\(y\in Y\)を\(y=x^2\)で対応させる、と言っているわけである。
つまりこの対応規則\(f\)は
$$(\forall x\in X)\ f(x)=x^2$$
ということである。
この\(f\)は単射ではない。
実際、\(x_1=1\)、\(x_2=-1\)とすると、\(f(x_1)=f(x_2)=1\)であるため、\(x\in X\)が相異なっていても同じ\(y\in Y\)と対応しているからである。
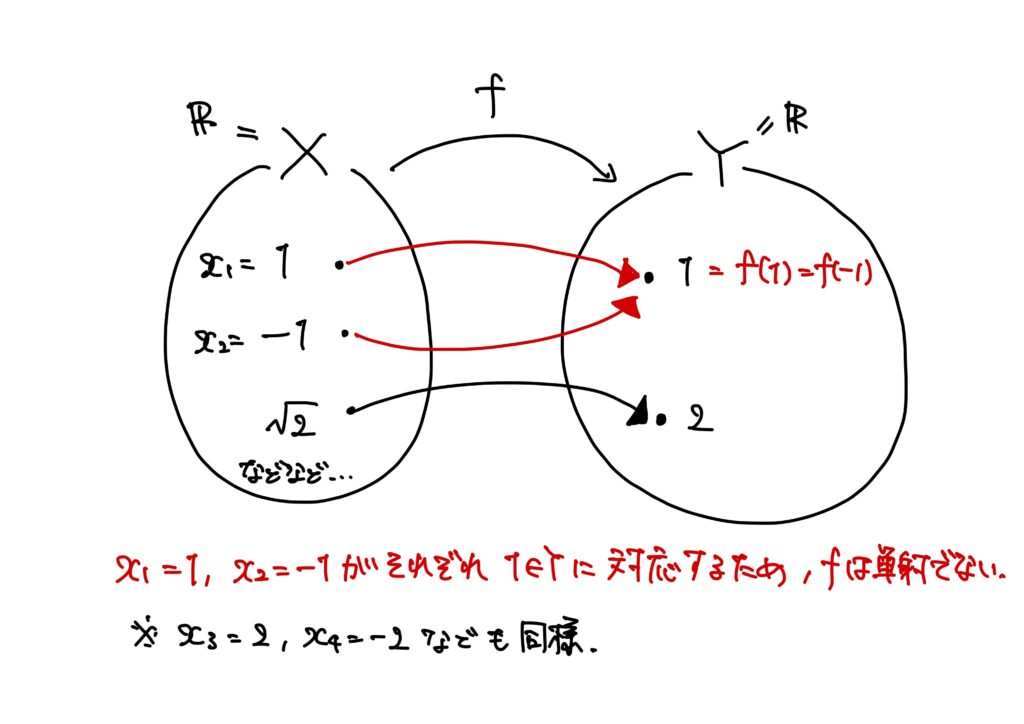
一方、\(X=Y=\mathbb{R}\)とした例3.は全射ではない。
というのも、負の実数\(y\in Y=\mathbb{R}\)が対応する\(x\in X=\mathbb{R}\)が存在しないからである。
例3’について
例3′.(実数値の関数のちょっと改変ver.)
\(X=Y=\{x\in\mathbb{R}\mid x\geq0\}\)とする。
このとき、写像\(f_0:X\to Y\)を\(f_0(x)=x^2\)で定める。
この\(f_0\)は全射である。
実際、任意の\(y\in Y\)に対して、\(\pm\sqrt{y}\in X\)が存在するからである。
ここで、この\(f_0\)は単射でもある。
なぜなら、任意の\(x_1,x_2\in X\)に対して、\(x_1\neq x_2\)ならば、\(f_0(x_1)=x_1^2\)であり、\(f_0(x_2)=x_2^2\)であるので、\(f_0(x_1)\neq f_0(x_2)\)であるからである。

まとめ
- 例1.は単射ではなく、全射でもない。
- 例1′.は単射であるが、全射でない。
- 例2は単射であるし、全射でもある。
- 例3.は単射ではなく、全射でもない。
- 例3′.は単射であり、全射でもある。
である。
従って、全単射なのは例2.と例3’である。
で、全単射って?
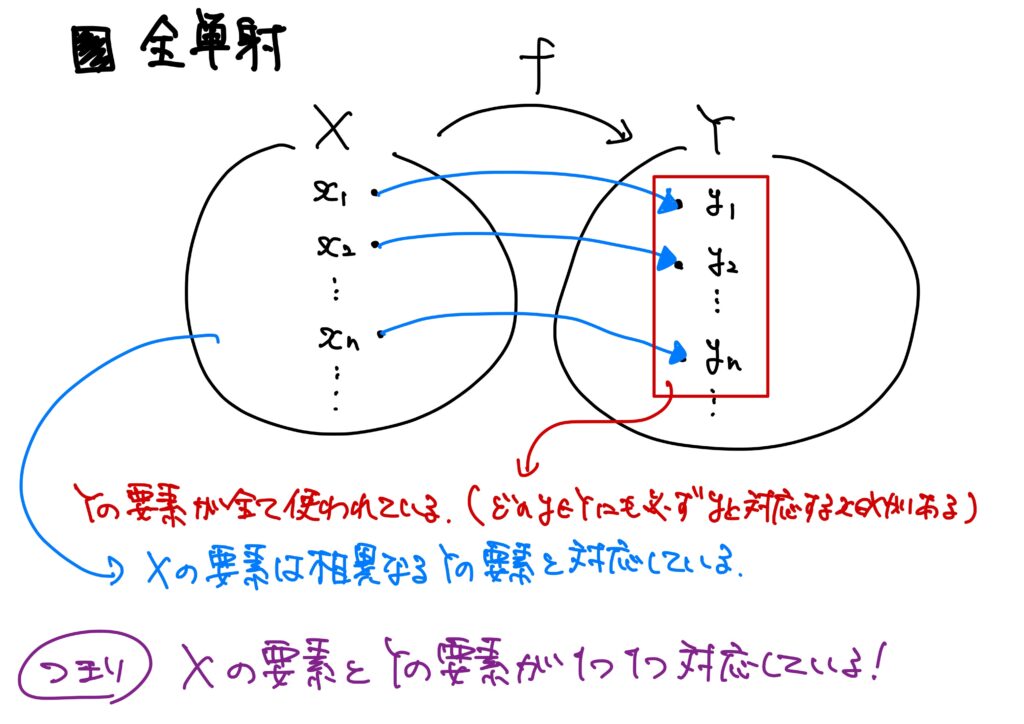
全単射を言い換えてみると、
ということである。
さらに言い換えれば、
ということである。
(※うまく言えなかった気がするので、「ん?」となったら下図を見てください。)
これを論理式で書けば、次である。
- \((\forall x,x’\in X)\ (f(x)= f(x’)\Rightarrow x=x’)\),
- \(f(X)=Y\)
余談(集合の濃度)
実は、全単射は逆写像(逆関数)の存在以外にも重要な役割を果たす。
それは集合の”濃度”である。
集合における濃度というのは、要素の数のことである。
これは簡単に数えられる程度の要素しかない集合に対してはあまり意味はないのだが、要素の数が有限個であっても膨大である場合や無限個である場合には誠に重宝する。
2つの集合において、濃度が等しい、平たく言えば要素の数が一致しているということはそれらの集合に全単射が存在するということなのである。
一つずつダブらずに対応してるんだから、要素の数は等しいよね、という発想である。
有限個の場合は「へーそーなんだー」で終わってしまうのだが、これが無限個の場合だと結構面白い(と思う)。
なぜかというと、自然数の集合\(\mathbb{N}\)と自然数の集合の直積集合\(\mathbb{N}^2\)は実は濃度が一致している。
すなわち、\(\mathbb{N}\)と\(\mathbb{N}^2\)の間には全単射が存在するので要素の数は同じでなのである。
筆者は最初、「んなわけあるか!嘘つくな!\(\mathbb{N}^2\)のほうが多いに決まっててんだろ!」と思ったのだが、なんとこれが本当に全単射が存在してしまうのである。
「無限って不思議だぁ…」と思った瞬間でもある。
興味があったら調べてみてほしい。
(※ちなみに、自然数の集合と偶数の集合にも全単射があるので濃度は一致してるヨ。)
結
今回は全単射について解説した。
全単射は単射かつ全射であるような写像のことを指す。
これを言い換えれば、
ということである。
次回は「逆写像」について解説する。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに、「集合・写像・論理ー数学の基本を学ぶ」の方が入門者にはオススメです!





コメントをする