「点列の極限の和・差と点列と数列の積の極限」【解析学の基礎シリーズ】点列編 その2

本記事の内容

本記事は点列の和・積、数列と点列の積の極限について解説する記事です。

本記事を読むにあたり、数列の極限と点列の極限を知っている必要があるため、その際は以下の記事を参照してください。

数列の収束って？〜直感から論理へ〜

本記事の内容本記事は「有界な単調列は収束する」という命題の証明に必要な、数列の極限を説明する記事です。この記事を読むにあたり、数列とはどういうものかを知っている必要があるため、以下の記事も合わせて御覧ください。収束の直感的なイメージとその例

for-spring.com

「点列って？」「点列の極限って？」【解析学の基礎シリーズ】点列編 その1

...

for-spring.com

2022.04.21

点列の極限の簡単な復習

点列の収束は

でした。
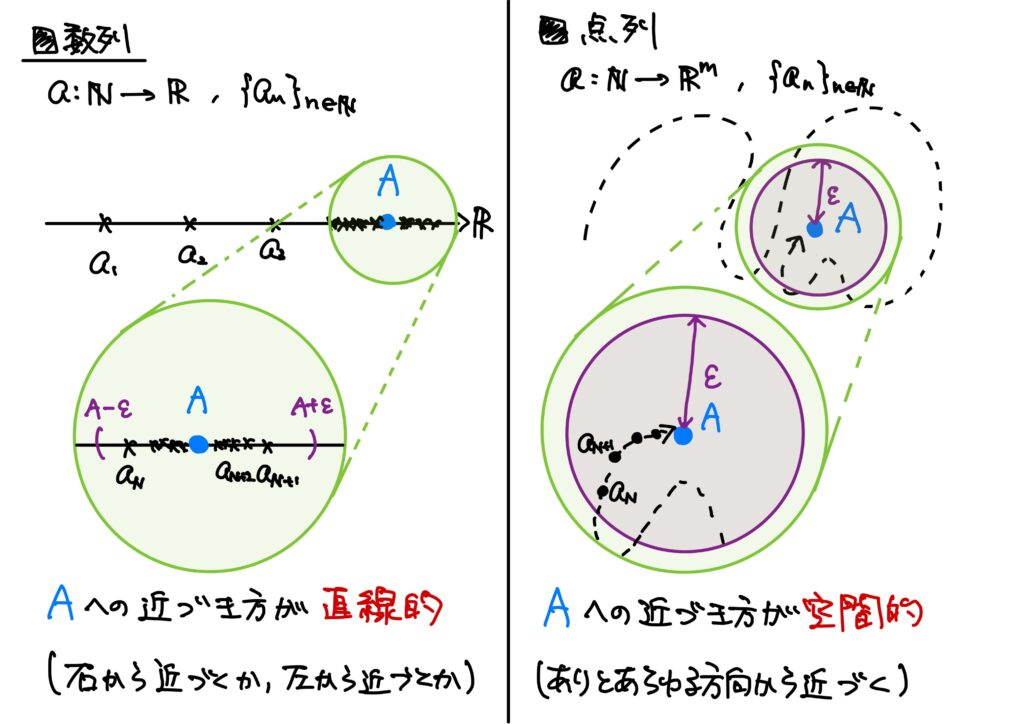
形式的には数列の極限と何ら変わらないのでした。
ただ、極限への近づき方が数列は直線的だったのに対して、点列は空間的だということでした。

さらに、この点列の収束と同値な命題がありました。
それが以下です。

要は、点列の極限は、個々の数列の極限のベクトルと一致しますよ、ということでした。
高校数学のノリでいうところの「$\lim$はカッコの中に入れてOK」ということです。
つまり

というわけです。

点列の極限の和・差

ベクトルに対しても和・差を考えることができますので、数列のときと同じように点列の極限にも和・差・積・商を考えることができます。

ただし、積・商については数列と同じようには行きません。
数列は結局値が実数でしたので、数列の積といったらば、結局は実数同士の積でした。
しかし、ベクトル同士で積は取れません(ベクトル同士の掛け算はできません)。

点列の場合の積は基本的に内積、外積です。
ただ、ベクトルは定数倍ができるので、そういう意味で点列と数列の積の極限を考えることができます。
今回はこれも示します。
同様に商も特殊といえば特殊です。(内積と外積と商は後の記事で解説します。)

さて、「何が成り立つのかネ？」ということですが、端的に言ってしまいましょう。

この証明は実は数列の極限の証明に帰着できます。
というのも定理1.が成り立っているためです。

つまり、
$$\boldsymbol{A}= \left( \begin{array}{c} A_1 \\ A_2 \\ \vdots \\ A_m \end{array} \right),\quad \boldsymbol{a}_n= \left( \begin{array}{c} a_{n,1} \\ a_{n,2} \\ \vdots \\ a_{n,m} \end{array} \right),\quad \boldsymbol{B}= \left( \begin{array}{c} B_1 \\ B_2 \\ \vdots \\ B_m \end{array} \right),\quad \boldsymbol{b}_n= \left( \begin{array}{c} b_{n,1} \\ b_{n,2} \\ \vdots \\ b_{n,m} \end{array} \right),$$
としたとき、定理1.から
$$\lim_{n\to\infty}(\boldsymbol{a}_n\pm\boldsymbol{b}_n)= \lim_{n\to\infty}\left( \begin{array}{c} \boldsymbol{a}_{n,1}\pm\boldsymbol{b}_{n,1} \\ \boldsymbol{a}_{n,2}\pm\boldsymbol{b}_{n,2} \\ \vdots \\ \boldsymbol{a}_{n,m}\pm\boldsymbol{b}_{n,m} \end{array} \right)= \left( \begin{array}{c} \displaystyle\lim_{n\to\infty}(\boldsymbol{a}_{n,1}\pm\boldsymbol{b}_{n,1}) \\ \displaystyle\lim_{n\to\infty}(\boldsymbol{a}_{n,2}\pm\boldsymbol{b}_{n,2})\\ \vdots \\ \displaystyle\lim_{n\to\infty}(\boldsymbol{a}_{n,m}\pm\boldsymbol{b}_{n,m}) \end{array} \right)$$
が成り立ちます。

従って、
$$\left( \begin{array}{c} \displaystyle\lim_{n\to\infty}(\boldsymbol{a}_{n,1}\pm\boldsymbol{b}_{n,1}) \\ \displaystyle\lim_{n\to\infty}(\boldsymbol{a}_{n,2}\pm\boldsymbol{b}_{n,2})\\ \vdots \\ \displaystyle\lim_{n\to\infty}(\boldsymbol{a}_{n,m}\pm\boldsymbol{b}_{n,m}) \end{array} \right)= \left( \begin{array}{c} A_1\pm B_1 \\ A_2\pm B_2 \\ \vdots \\ A_m\pm B_m \end{array} \right)$$
であれば証明が完了です。
すなわち、$1\leq i\leq m$なる任意の$i\in\mathbb{N}$で
$$\lim_{n\to\infty}(a_{n,i}\pm b_{n,i})=A_i\pm B_i$$
であればよいのです。
これは、$a_{n,i}$、$b_{n,i}$がそれぞれ数列$\{a_{n,i}\}_{n\in\mathbb{N}}$、$\{b_{n,i}\}_{n\in\mathbb{N}}$の項ですので、数列の極限に帰着できることを指しています。

つまり、次を示せば良いことになります。

$\displaystyle \lim_{n\to\infty}(a_n-b_n)=\lim_{n\to\infty}a_n-\lim_{n\to\infty}b_n$の場合は、$\displaystyle \lim_{n\to\infty}(a_n+b_n)=\lim_{n\to\infty}a_n+\lim_{n\to\infty}b_n$の場合において$b_n$を$-b_n$にすれば良いので$\displaystyle \lim_{n\to\infty}(a_n+b_n)=\lim_{n\to\infty}a_n+\lim_{n\to\infty}b_n$を示します。

証明

示したいことは
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |(a_n+b_n)-(A+B)|<\epsilon)$$
です。
今、$\displaystyle \lim_{n\to\infty}a_n=A$および$\displaystyle \lim_{n\to\infty}b_n=B$が成り立っているため、
$$(\forall \epsilon_a>0)(\exists N_a\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N_a\Rightarrow |a_n-A|<\epsilon_a)$$
かつ
$$(\forall \epsilon_b>0)(\exists N_b\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N_b\Rightarrow |b_n-B|<\epsilon_b)$$
が成り立っています。
いつもの通りに、$N$を見つけるために$|(a_n+b_n)-(A+B)|$を変形してみましょう。
すると、

$$\begin{eqnarray} |(a_n+b_n)-(A+B)|=|(a_n-A)+(b_n-B)|\leq |a_n-A|+|b_n-B| \end{eqnarray}$$
となります。
今、任意の$\epsilon_a>0$に対して$n\geq N_a$なる$n\in\mathbb{N}$においては$|a_n-A|<\epsilon_a$が、任意の$\epsilon_b>0$に対して$n\geq N_b$なる$n\in\mathbb{N}$においては$|b_n-B|<\epsilon_b$が成り立っています。
従って、$N$として$N_a$と$N_b$のうち大きい方を採用すればよいことが分かります。
また、$\epsilon_a>0$と$\epsilon_b>0$は任意だったので、任意の$\epsilon>0$を使って新たに$\displaystyle \frac{\epsilon}{2}>0$と書き直します。
故に、$N=\max\{N_a,N_b\}$とすることで、
$n\geq N$なる$n\in\mathbb{N}$に対して

$$\begin{eqnarray} |(a_n+b_n)-(A+B)|=|(a_n-A)+(b_n-B)|\leq |a_n-A|+|b_n-B|<\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon \end{eqnarray}$$
が成り立ちます。
従って、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |(a_n+b_n)-(A+B)|<\epsilon)$$
です。
故に$\displaystyle \lim_{n\to\infty}(a_n+b_n)=\lim_{n\to\infty}a_n+\lim_{n\to\infty}b_n$です。

$\displaystyle \lim_{n\to\infty}(a_n-b_n)=\lim_{n\to\infty}a_n-\lim_{n\to\infty}b_n$の場合は、
今の証明を$b_n$を$-b_n$に書き換えれば証明できます。

証明終わり

従って、点列の極限の和・差が成り立ちます。

次に、点列と数列の積の極限を考えます。

点列と数列の積の極限

ベクトル同士に単なる積は取れません。
ベクトルにおける積は内積と外積の２種類があります。
ただ、ベクトルには定数倍ができるので、本節ではそういう意味で点列と数列の積の極限を考えます。

「どういうことかネ？」となるかもしれないので、主張を明示してしまいましょう。

字面だけを見ると「単なる積に見えるがネ」と思うかもしれませんが、これはベクトルのスカラー倍です。
実際、
$$\boldsymbol{A}= \left( \begin{array}{c} A_1 \\ A_2 \\ \vdots \\ A_m \end{array} \right),\quad \boldsymbol{a}_n= \left( \begin{array}{c} a_{n,1} \\ a_{n,2} \\ \vdots \\ a_{n,m} \end{array} \right)$$
としたとき、
$$\lim_{n\to\infty}(k_n\boldsymbol{a}_n)=\lim_{n\to\infty}k_n \left( \begin{array}{c} a_{n,1} \\ a_{n,2} \\ \vdots \\ a_{n,m} \end{array} \right)=\lim_{n\to\infty} \left( \begin{array}{c} k_n\cdot a_{n,1} \\ k_n\cdot a_{n,2} \\ \vdots \\ k_n\cdot a_{n,m} \end{array} \right)$$
だからです。
さらに、定理1.から
$$\lim_{n\to\infty} \left( \begin{array}{c} k_n\cdot a_{n,1} \\ k_n\cdot a_{n,2} \\ \vdots \\ k_n\cdot a_{n,m} \end{array} \right)= \left( \begin{array}{c} \displaystyle\lim_{n\to\infty}(k_n\cdot a_{n,1}) \\ \displaystyle\lim_{n\to\infty}(k_n\cdot a_{n,2})\\ \vdots \\ \displaystyle\lim_{n\to\infty}(k_n\cdot a_{n,m}) \end{array} \right)$$
ですので、この場合も数列の場合に帰着できます。
従って、次を示せば良いことになります。

証明

示したいことは
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |a_nb_n-AB|<\epsilon)$$
です。
今、$\displaystyle \lim_{n\to\infty}a_n=A$および$\displaystyle \lim_{n\to\infty}b_n=B$が成り立っているため、
$$(\forall \epsilon_a>0)(\exists N_a\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N_a\Rightarrow |a_n-A|<\epsilon_a)$$
かつ
$$(\forall \epsilon_b>0)(\exists N_b\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N_b\Rightarrow |b_n-B|<\epsilon_b)$$
が成り立っています。

いつもの通りに、$N$を見つけるために$|a_nb_n-AB|$を変形してみましょう。
目標としては$|a_n-A|$と$|b_n-B|$を出したいわけです。
そういう立場に立った状態で変形してみましょう。
とはいえ、実は同じような考え方を既に関数の極限でしています。

$$\begin{eqnarray} |a_nb_n-AB|&=&|a_n-b_n-a_nB+a_nB-AB|\\ &\leq&|a_nb_n-a_nB|+|a_nB-AB|\\ &=&|a_n|\cdot|b_n-B|+|a_n-A|\cdot|B| \end{eqnarray}$$
となります。
従って、$|a_n|$が有界であれば、つまりある$M\in\mathbb{R}$が存在して$a_n\leq M$が成り立てば、$\epsilon_a$と$\epsilon_b$をうまく帳尻合わせることで証明が完了です。
実は、そういう$M$は存在します。
つまり、次が成り立ちます。

補題2.の証明

実数列$\{a_n\}_{n\in\mathbb{N}}$が$A\in\mathbb{R}$に収束するとします。
つまり
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |a_n-A|<\epsilon)$$
が成り立っています。
つまり、$n\geq N$なる$n\in\mathbb{N}$に対しては
$$A-\epsilon<a_n<A+\epsilon$$
が成り立っています。
従って、$|a_n|<|A-\epsilon|$または$|a_n|<|A+\epsilon|$が成り立っています。
故に$M’=\max{|A-\epsilon|,|A+\epsilon|}$とすれば、
$n\geq N$なる$n\in\mathbb{N}$に対しては$|a_n|<M’$です。

次に、$1\leq n< N$という$n\in\mathbb{N}$について考えてみましょう。
$1\leq n< N$という$n\in\mathbb{N}$に対しては$\{a_n\}$の値は有限個です。
従って、$M=\max\{|a_1|,|a_2|,\dots ,|a_{N-1}|,M’\}$とすることで、$1\leq n< N$という$n\in\mathbb{N}$についても$n\geq N$という$n\in\mathbb{N}$についても、すなわち任意の$n\in\mathbb{N}$に対して$|a_n|\leq M$です。

補題2.の証明終わり

では、数列の極限の積の証明に戻ります。

今、
$$\begin{eqnarray} |a_nb_n-AB|&=&|a_n-b_n-a_nB+a_nB-AB|\\ &\leq&|a_nb_n-a_nB|+|a_nB-AB|\\ &=&|a_n|\cdot|b_n-B|+|a_n-A|\cdot|B| \end{eqnarray}$$
が成り立っているのでした。
更に補題2.から、ある$M\in\mathbb{R}$が存在して、任意の$n\in\mathbb{N}$に対して$|a_n|\leq M$でした。
従って、
$$\begin{eqnarray} |a_n|\cdot|b_n-B|+|a_n-A|\cdot|B|\leq M\cdot |b_n-B|+|a_n-A|\cdot |B| \end{eqnarray}$$
が成り立ちます。
加えて、今
$$(\forall \epsilon_a>0)(\exists N_a\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N_a\Rightarrow |a_n-A|<\epsilon_a)$$
かつ
$$(\forall \epsilon_b>0)(\exists N_b\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N_b\Rightarrow |b_n-B|<\epsilon_b)$$
が成り立っているのでした。
$\epsilon_a>0$と$\epsilon_b>0$は任意だったので、帳尻を合わせるために任意の$\epsilon>0$を用いて$\displaystyle\epsilon_a=\frac{\epsilon}{2|B|}$、$\displaystyle\epsilon_b=\frac{\epsilon}{2M}$としても成り立ちます。従って、
$$\begin{eqnarray} |a_nb_n-AB|&=&|a_n-b_n-a_nB+a_nB-AB|\\ &\leq&|a_nb_n-a_nB|+|a_nB-AB|\\ &=&|a_n|\cdot|b_n-B|+|a_n-A|\cdot|B|\\ &\leq& M\cdot |b_n-B|+|a_n-A|\cdot |B|\\ &=&M\cdot \frac{\epsilon}{2M}+\frac{\epsilon}{2|B|}\cdot |B|\\ &=&\epsilon \end{eqnarray}$$
従って、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |a_nb_n-AB|<\epsilon)$$
が成り立ちます。

証明終わり

本当に成り立つのかネ？

成り立ちます。
「ついさっき成り立つことを証明しましたよね局長？」と言いたいところですが、しかし一方で例があったほうが説得力があると思いますので、２つほど例を紹介します。

例3.(和差の例)
$$\boldsymbol{A}= \left( \begin{array}{c} 0 \\ 2 \\ \end{array} \right),\quad \boldsymbol{a}_n= \left( \begin{array}{c} \displaystyle \frac{1}{n} \\ 2 \\ \end{array} \right),\quad \boldsymbol{B}= \left( \begin{array}{c} 1 \\ 1\\ \end{array} \right),\quad \boldsymbol{b}_n= \left( \begin{array}{c} \displaystyle 1+\frac{1}{n} \\ \displaystyle \frac{n+2}{n} \\ \end{array} \right),$$
とします。
このとき、
$$\lim_{n\to\infty}\boldsymbol{a}_n=A,\quad \lim_{n\to\infty}\boldsymbol{b}_n=B$$
です。
これは前回(【解析学の基礎シリーズ】関数の極限編 その19)で証明しています。
このとき、定理1.から
$$\lim_{n\to\infty}(\boldsymbol{a}_n+\boldsymbol{b}_n)= \lim_{n\to\infty}\left( \begin{array}{c} \displaystyle \left(\frac{1}{n}\right)+\left(1+\frac{1}{n}\right)\\ \displaystyle (2)+\left(\frac{n+2}{n}\right)\\ \end{array} \right)= \left( \begin{array}{c} \displaystyle\lim_{n\to\infty}\left(1+\frac{2}{n}\right) \\ \displaystyle\lim_{n\to\infty}\left(3+\frac{2}{n}\right)\\ \end{array} \right)= \left( \begin{array}{c} 1 \\ 3\\ \end{array} \right)= A+B$$
です。

例4.(点列と数列の積の極限)
$$\boldsymbol{A}= \left( \begin{array}{c} 0 \\ 2 \\ \end{array} \right),\quad \boldsymbol{a}_n= \left( \begin{array}{c} \displaystyle \frac{1}{n} \\ 2 \\ \end{array} \right),\quad k_n=\frac{n+4}{3n}$$
とします。
このとき、
$$\lim_{n\to\infty}\boldsymbol{a}_n=A,\quad \lim_{n\to\infty}k_n=\frac{1}{3}$$
です。
これもすでに前回(【解析学の基礎シリーズ】関数の極限編 その19)で証明しています。
(厳密にこれを証明しているわけではありませんが、同じ方法でできます。$n+1$の部分を$n+4$に変えて、分母の$n$を$3n$に変えるだけです。)
このとき、定理1.から
$$\lim_{n\to\infty}(k_n\boldsymbol{a}_n)= \lim_{n\to\infty}\left( \begin{array}{c} \displaystyle \left( \frac{n+4}{3n} \right)\cdot\left(\frac{1}{n}\right)\\ \displaystyle \left( \frac{n+4}{3n} \right)\cdot\left(\frac{n+2}{n}\right)\\ \end{array} \right)= \left( \begin{array}{c} \displaystyle\lim_{n\to\infty} \left( \frac{n+4}{3n}\cdot\frac{1}{n}\right)\\ \displaystyle\lim_{n\to\infty}\left( \frac{n+4}{3n}\cdot\frac{n+2}{n}\right)\\ \end{array} \right)$$
です。
さらに、数列の極限の積から、
$$\left( \begin{array}{c} \displaystyle\lim_{n\to\infty} \left( \frac{n+4}{3n}\cdot\frac{1}{n}\right)\\ \displaystyle\lim_{n\to\infty}\left( \frac{n+4}{3n}\cdot\frac{n+2}{n}\right)\\ \end{array} \right)= \left( \begin{array}{c} \displaystyle\left( \lim_{n\to\infty} \frac{n+4}{3n}\right)\cdot\left(\lim_{n\to\infty}\frac{1}{n}\right)\\ \displaystyle\left(\lim_{n\to\infty}\frac{n+4}{3n}\right)\cdot\left(\lim_{n\to\infty}\frac{n+2}{n}\right)\\ \end{array} \right)= \left( \begin{array}{c} 0 \\ \displaystyle \frac{2}{3}\\ \end{array} \right)= \frac{1}{3}A$$
です。

結

今回は点列の和差の極限と点列と数列の積の極限について解説しました。

結局の所、数列の場合に帰着できる、というわけです。
しかしながら、点列における、というよりベクトルにおける積は内積と外積がありますので、数列と全く同じというわけではありません。

次回は点列の内積の極限について解説します。

乞うご期待！質問、コメントなどお待ちしております！