本記事の内容
本記事は、ヤコビ行列、勾配について解説する記事です。
本記事を読むにあたり、偏微分と全微分について知っている必要があるため、以下の記事も合わせてご覧ください。
↓偏微分の記事
↓全微分の記事
1変数の微分と多変数の微分(偏微分)との違い
1変数の微分と多変数の微分との違いは、勿論変数の数なのですが、それ故微分係数の風貌が変わります。
微分係数は、その点における接線の傾きなので、その瞬間の変化量を表しています。
1変数実数値関数の場合の微分係数は勿論実数値です。
1変数ベクトル値関数の場合の微分係数はベクトルですが、ベクトル値の各関数の微分係数を並べたベクトルです。
確かに、1変数の場合でも微分係数は実数値だったりベクトル値だったりするわけですが、結局の所1変数実数値関数の微分係数を求めるという点においては違いはありません。
それ故、微分係数はなんだかんだ接線の傾きを表しています。
一方で、多変数の場合はそもそも複数の変数で微分するわけですので、偏微分係数は複数あります。
例えば、2変数であれば\(\displaystyle\frac{\partial f}{\partial x}(\boldsymbol{a})\)と\(\displaystyle\frac{\partial f}{\partial y}(\boldsymbol{a})\)のように。
さらに、多変数の場合は全微分というものもあるので、全微分係数まで含めるとさらに種類が多くなります。
先程、1変数の場合の微分係数は接線の傾きを表してるよ、という話でしたが、多変数の場合は接平面の傾き(みたいなもの)になります。
接線は、接線方向のベクトル1つが分かれば、そのベクトルを定数倍することで得られる直線がそのまま接線になります。
しかし、接平面の場合はそうも行きません。
2変数の場合は\(x\)方向の変化量のベクトル(\(x\)の偏微分係数)と\(y\)方向の変化量のベクトル(\(y\)の偏微分係数)が張る平面が接平面になります。
つまり何が言いたいか、というと1変数の場合の微分係数は接線の方程式の傾きを表しており、多変数の場合は各変数の偏微分係数を並べたベクトルにより張られる平面によって接平面が得られる、ということになります。
結局は「多変数はベクトルで考えるんだ」ということです。
それに伴い出現する新たなコンセプトがヤコビ行列と勾配です。
まずは、全微分とヤコビ行列を軽く復習します。
全微分可能性、全微分係数、導関数
\(\Omega\)は\(\mathbb{R}^n\)の開集合、\(\boldsymbol{f}:\Omega\to\mathbb{R}^m\)、\(M(m,n;\mathbb{R})\)を\((m,n)\)型の実行列の集合とする。すなわち、 $$ M(m,n;\mathbb{R})=\left\{A=\left(a_{ij}\right)\middle|a_{ij}\in\mathbb{R}\ (1\leq \forall i\leq m,\ 1\leq \forall j\leq n)\right\} $$ とする。- \(\boldsymbol{a}\in\Omega\)で全微分可能 \(\boldsymbol{a}\in\Omega\)とする。\(\boldsymbol{f}\)が\(\boldsymbol{a}\)で(全)微分可能((totally) differentiable at \(\boldsymbol{a}\))であるとは、 $$ \left( \exists A\in M(m,n;\mathbb{R})\right)\ {\rm s.t.}\ \lim_{\boldsymbol{h}\to\boldsymbol{0}}\frac{1}{\|\boldsymbol{h}\|}\left( \boldsymbol{f}(\boldsymbol{a}+\boldsymbol{h})-\boldsymbol{f}(\boldsymbol{a})-A\boldsymbol{h}\right)=\boldsymbol{0} $$ が成り立つことをいう。このとき、\(A\)を\(\boldsymbol{f}\)の\(\boldsymbol{a}\)における(全)微分係数((totally) derivative of \(\boldsymbol{f}\) at \(\boldsymbol{a}\), the (total) differential of \(\boldsymbol{f}\) at \(\boldsymbol{a}\))とよび、\(\boldsymbol{f}^\prime(\boldsymbol{a})\)で表す。
- \(\Omega\)で全微分可能 \(\boldsymbol{f}\)が\(\Omega\)で(全)微分可能であるとは、\(\forall \boldsymbol{x}\in\Omega\)で全微分可能であることをいう。このとき $$ \Omega\ni\boldsymbol{x}\mapsto \boldsymbol{f}^\prime(\boldsymbol{x})\in M(m,n;\mathbb{R}) $$ を\(\boldsymbol{f}\)の導関数と呼び、\(\boldsymbol{f}^\prime\)で表す。
全微分とは、上記の事でした。
そして、上記の行列\(A\)が実はヤコビ行列になるのでした。
ヤコビ行列というのは以下でした。
ヤコビ行列(ヤコビアン)
\(\Omega\)を\(\mathbb{R}^n\)の開集合、\(\boldsymbol{a}\in\Omega\)、\(\boldsymbol{f}:\Omega\to\mathbb{R}^m\)が\(\boldsymbol{a}\)で全微分可能とし、 $$ \boldsymbol{f}= \left( \begin{array}{c} f_1\\ f_2\\ \vdots\\ f_m \end{array} \right),\quad \boldsymbol{x}=\left( \begin{array}{c} x_1\\ x_2\\ \vdots\\ x_n \end{array} \right) $$と書いたとする。このとき、行列 $$ \boldsymbol{f}^\prime(\boldsymbol{a})=\left(\frac{\partial f_i}{\partial x_j}(\boldsymbol{a}) \right)= \begin{pmatrix} \displaystyle\frac{\partial f_1}{\partial x_1}(\boldsymbol{a})&\displaystyle\frac{\partial f_1}{\partial x_2}(\boldsymbol{a})&\cdots &\displaystyle\frac{\partial f_1}{\partial x_n}(\boldsymbol{a})\\ \displaystyle\frac{\partial f_2}{\partial x_1}(\boldsymbol{a})&\displaystyle\frac{\partial f_2}{\partial x_2}(\boldsymbol{a})&\cdots &\displaystyle\frac{\partial f_2}{\partial x_n}(\boldsymbol{a})\\ \vdots&\vdots& \ddots&\vdots\\ \displaystyle\frac{\partial f_m}{\partial x_1}(\boldsymbol{a})&\displaystyle\frac{\partial f_m}{\partial x_2}(\boldsymbol{a})&\cdots &\displaystyle\frac{\partial f_m}{\partial x_n}(\boldsymbol{a})\\ \end{pmatrix} $$ を\(\boldsymbol{f}\)の\(\boldsymbol{a}\)におけるヤコビ行列またはヤコビアン(the Jacobian matrix of \(\boldsymbol{f}\) at \(\boldsymbol{a}\))と呼ぶ。つまり、ここで何が言いたいのか、というと、
ということです。
与えられた関数が多変数ベクトル値関数の場合、その全微分係数と言われたらば「ああ、この係数ってのは行列なのね」と直ちに思ってほしい、ということです。
ちなみに、前回サラッと紹介した全微分の「\(df=\)うんぬん」という式(というより記号)は”微分形式”と呼ばれるもので、実は数学的に意味がある式です。
勾配(gradient)
勾配はなんてことありません。
言ってしまえば、勾配はヤコビ行列の一部です。
勾配って結局なんですか?
先程、勾配はヤコビ行列の一部だ、と述べましたが本当にそれだけなんです。
更に言ってしまえば「多変数実数値関数の場合のヤコビ行列」ということです。
勾配ベクトル(gradient)
\(\Omega\)は\(\mathbb{R}^n\)の開集合、\(\boldsymbol{a}\in\Omega\)、\(f:\Omega\to\mathbb{R}\)に対して $$ \boldsymbol{x}=\left( \begin{array}{c} x_1\\ x_2\\ \vdots\\ x_n \end{array} \right) $$ と書いたとする。このとき $$ \left( \frac{\partial f}{\partial x_1}\ \frac{\partial f}{\partial x_2}\ \cdots\ \frac{\partial f}{\partial x_n}\right) $$ を転置した\(n\)次元縦ベクトルを\({\rm grad}f(\boldsymbol{a})\)または\(\nabla f(\boldsymbol{a})\)で表し、\(f\)の\(\boldsymbol{a}\)における勾配ベクトル(gradient)と呼ぶ。すなわち $$ {\rm grad}f(\boldsymbol{a})=\nabla f(\boldsymbol{a}) =\left( \begin{array}{c} \displaystyle\frac{\partial f}{\partial x_1}\\ \displaystyle\frac{\partial f}{\partial x_2}\\ \vdots\\ \displaystyle\frac{\partial f}{\partial x_n} \end{array} \right) $$ である。記号\(\nabla\)は単独でもナブラ(nabla)と呼ばれ、 $$ \nabla =\left( \begin{array}{c} \displaystyle\frac{\partial }{\partial x_1}\\ \displaystyle\frac{\partial }{\partial x_2}\\ \vdots\\ \displaystyle\frac{\partial }{\partial x_n} \end{array} \right) $$ という意味で、関数\(f\)に対して勾配ベクトルを対応させる写像としても用いられる。これはまさにヤコビ行列\(\displaystyle A=\left(\frac{\partial f_i}{\partial x_j}(\boldsymbol{a}) \right)\)の\(m=1\)の場合を転置したベクトルに相当します。
勾配ベクトルはいわゆるベクトル解析で頻繁に出現します。
勾配ベクトルのイメージ
勾配ベクトルはもう殆どベクトル解析の範疇ですので、あまり込み入った説明はしませんが、やはりイメージは重要です。
結論から言うと、勾配ベクトルのイメージは(個人的に)2つあると思います。
それが
- 接平面の傾き
- 勾配ベクトル\({\rm grad}f\)の向き\(=\)\(f\)の値が最も激しく変化する向き
です。
1.について(接平面の傾き)
1.については線型代数を学んでいると一撃で見て分かる方法があります。
(※イメージですので、2変数の場合を述べます。)
\(f(x,y)\)の勾配ベクトル\({\rm grad}f\)は
$$
{\rm grad}f=
\left(
\begin{array}{c}
\displaystyle\frac{\partial f}{\partial x}\\
\displaystyle\frac{\partial f}{\partial y}\\
\end{array}
\right)
$$
でした。
これを\(\mathbb{R}^2\)の正規直交基底\(\displaystyle \boldsymbol{e}_1=\left(
\begin{array}{c}
1\\
0
\end{array}
\right)\)、\(\displaystyle \boldsymbol{e}_ 2=\left(
\begin{array}{c}
0\\
1
\end{array}
\right)\)を用いて表すと、
$$
{\rm grad}f=
\frac{\partial f}{\partial x}
\left(
\begin{array}{c}
1\\
0
\end{array}
\right)+
\frac{\partial f}{\partial y}
\left(
\begin{array}{c}
0\\
1
\end{array}
\right)
$$
となります。
正規直交基底\(\boldsymbol{e}_1\)、\(\boldsymbol{e}_2\)は座標軸の役割があるということでしたので、まさに\({\rm grad}f\)は平面を作ることができます。
そしてその座標は\(\displaystyle\left( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\right)\)ですので、\(f\)各方向の変化量です。
従って、接平面の傾きに対応しています。
もっというと、ベクトル\(\displaystyle
\left(
\begin{array}{c}
\displaystyle\frac{\partial f}{\partial x}\\
0
\end{array}
\right)
\)と\(\displaystyle
\left(
\begin{array}{c}
0\\
\displaystyle\frac{\partial f}{\partial y}
\end{array}
\right)
\)
の線型結合の集合
$$
\left\{c_1\left(
\begin{array}{c}
\displaystyle\frac{\partial f}{\partial x}\\
0
\end{array}
\right)+
c_2\left(
\begin{array}{c}
0\\
\displaystyle\frac{\partial f}{\partial y}
\end{array}
\right)\middle|c_1,c_2\in\mathbb{R}\right\}
$$
が接平面となるわけです。
2.について(勾配ベクトル\({\rm grad}f\)の向き\(=\)\(f\)の値が最も激しく変化する向き)
こちらのほうがイメージが湧きやすいかもしれません。
図と共に説明します。
\(f(x,y,z)\)という関数を考えます。
このとき、3次元空間上のある\(\boldsymbol{r}=(x,y,z)\)という点においての勾配ベクトル\({\rm grad}f(\boldsymbol{r})\)は
$$
{\rm grad}f(\boldsymbol{r})=
\left(
\begin{array}{c}
\displaystyle\frac{\partial f}{\partial x}\\
\displaystyle\frac{\partial f}{\partial y}
\end{array}
\right)
$$
です。
このとき、\(\Delta\boldsymbol{r}=(\Delta x,\Delta y,\Delta z)\in\mathbb{R}^3\)としたとき、\(\boldsymbol{r}\)からほんのちょっとだけ動かした点\(\boldsymbol{r}+\Delta\boldsymbol{r}=(x+\Delta x,y+\Delta y,z+\Delta z)\)に対しても\(f\)の値が定まっているとして、この\(\boldsymbol{r}+\Delta\boldsymbol{r}\)について考えてみます。
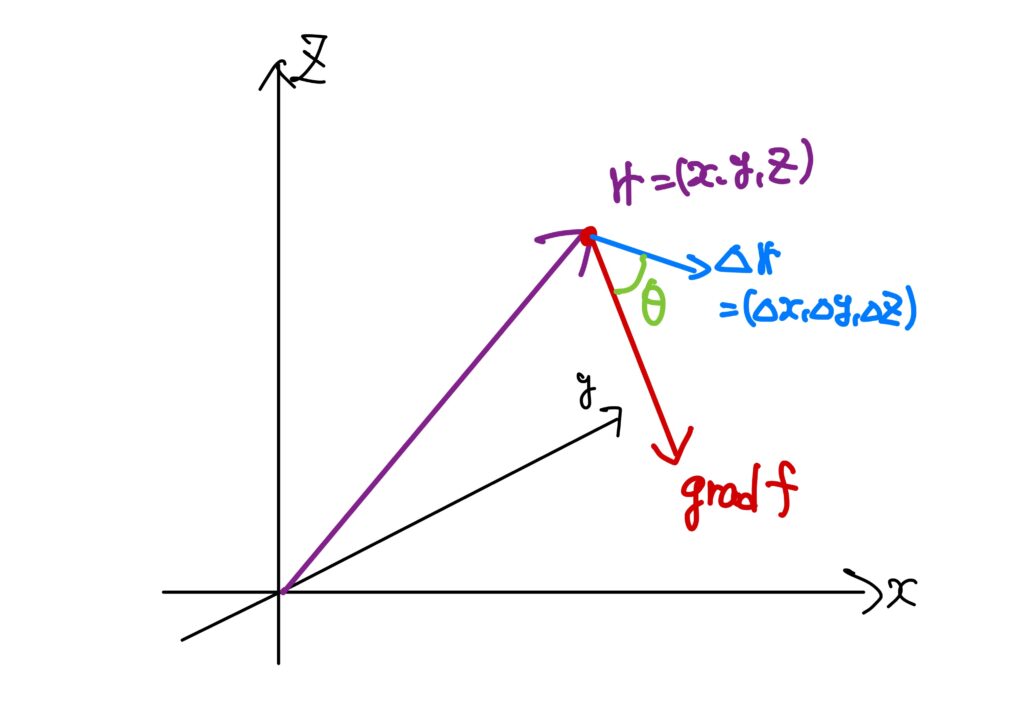
そして、\({\rm grad}f\)と\(\Delta\boldsymbol{r}\)のなす角を\(\theta\ (\theta\in[0,2\pi))\)とします。
このとき、\(\boldsymbol{r}+\Delta\boldsymbol{r}\)での\(f\)値\(f(\boldsymbol{r}+\Delta\boldsymbol{r})\)と\(f(\boldsymbol{r})\)の差を計算してみます。
\begin{eqnarray}
f(\boldsymbol{r}+\Delta\boldsymbol{r})-f(\boldsymbol{r})&=&
f(x+\Delta x,y+\Delta y,z+\Delta z)-f(x,y,z)\\
&=&\color{red}{f(x,y,z)+\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z}-f(x,y,z)\\
&=&\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z
\end{eqnarray}
となります。
ただし、赤字の部分の等式
$$
f(x+\Delta x,y+\Delta y,z+\Delta z)=f(x,y,z)+\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z
$$
については、多変数の場合のテイラー展開を用いました。
まだ学習していないので、「ふーん。そーなんだー。」と思ってください。
さて、
\begin{eqnarray}
f(\boldsymbol{r}+\Delta\boldsymbol{r})-f(\boldsymbol{r})&=&\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z
\end{eqnarray}
が分かりました。
これは内積を使って表すことができます。
すなわち、
\begin{eqnarray}
\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z&=&
\left(\left(
\begin{array}{c}
\displaystyle\frac{\partial f}{\partial x}\\
\displaystyle\frac{\partial f}{\partial y}\\
\displaystyle\frac{\partial f}{\partial z}
\end{array}
\right),
\left(
\begin{array}{c}
\Delta x\\
\Delta y\\
\Delta z
\end{array}
\right)\right)\\
&=&
\left( {\rm grad}f,\Delta \boldsymbol{r}\right)\\
&=&\|{\rm grad}f\|\cdot\|\Delta\boldsymbol{r}\|\cdot \cos\theta
\end{eqnarray}
となります。式\(\|{\rm grad}f\|\cdot\|\Delta\boldsymbol{r}\|\cdot \cos\theta\)において、\(\|{\rm grad}f\|\cdot\|\Delta\boldsymbol{r}\|\)は\(\theta\)に依存しません。
すなわち、固定の値で、動くのはあくまで\(\theta\)です。
ということは、式
$$
f(\boldsymbol{r}+\Delta\boldsymbol{r})-f(\boldsymbol{r})=\|{\rm grad}f\|\cdot\|\Delta\boldsymbol{r}\|\cdot \cos\theta
$$
を最大にするような\(\theta\)は\(\theta\in[0,2\pi)\)で\(\theta=0\)のときです。
つまり、何が言いたいかと言うと、
ということです。
ここで、\(\theta\)は何者だったかと言うと、\({\rm grad}f\)と\(\Delta\boldsymbol{r}\)のなす角でした。
\(\theta=0\)のときに\(f(\boldsymbol{r}+\Delta\boldsymbol{r})-f(\boldsymbol{r})\)の値を最大化するので、まさに\({\rm grad}f\)の方向が最も変化が激しい方向ということになります。
実際に計算してみましょう!
簡単ではありますが、実際に計算してみます。
例1.(2変数2次関数) \(f(x,y)=x^2+2xy+y^2+x+y+1\)が全微分可能かどうかを調べて、\(f\)のヤコビ行列と\({\rm grad}f\)を求めてみます。
\(\displaystyle\frac{\partial f}{\partial x}\)と\(\displaystyle\frac{\partial f}{\partial y}\)は共に多項式関数なので連続です。
従って、\(f\)は\(C^1\)級ですから全微分可能です。
ただし、ここで次の事実を使いました。
定理2.
\(\Omega\)は\(\mathbb{R}^n\)の開集合、\(\boldsymbol{f}:\Omega\to\mathbb{R}^m\)はすべての変数\(x_j\)に対して\(\Omega\)で偏微分可能で、偏導関数\(\displaystyle\frac{\partial \boldsymbol{f}}{\partial x_j}:\Omega\to\mathbb{R}^m\)は連続だとする。このとき、\(\boldsymbol{f}\)は\(\Omega\)で全微分可能である。この定理2.の証明は【解析学の基礎シリーズ】偏微分編 その3を御覧ください。
さて、全微分可能であることが分かりましたので、\(f\)のヤコビ行列\(f^\prime(x,y)\)を求めてみます。
ヤコビ行列と言っても実数値関数ですので今回は横ベクトルになります。
$$
f^\prime(x,y)=\left( \frac{\partial f}{\partial x}\ \frac{\partial f}{\partial y}\right)=(2x+2y+1\ 2y+2x+1)
$$
また、\({\rm grad}f=f^\prime(x,y)^\top\)だったわけですので、
$$
{\rm grad}f(x,y)=
\left(
\begin{array}{c}
\frac{\partial f}{\partial x}\\
\frac{\partial f}{\partial y}
\end{array}
\right)=
\left(
\begin{array}{c}
2x+2y+1\\
2y+2x+1
\end{array}
\right)
$$
となります。
\({\rm grad}f(a,b)\)は\((a,b)\)からの\(f\)の値の変化が最も激しい方向を指すのでした。
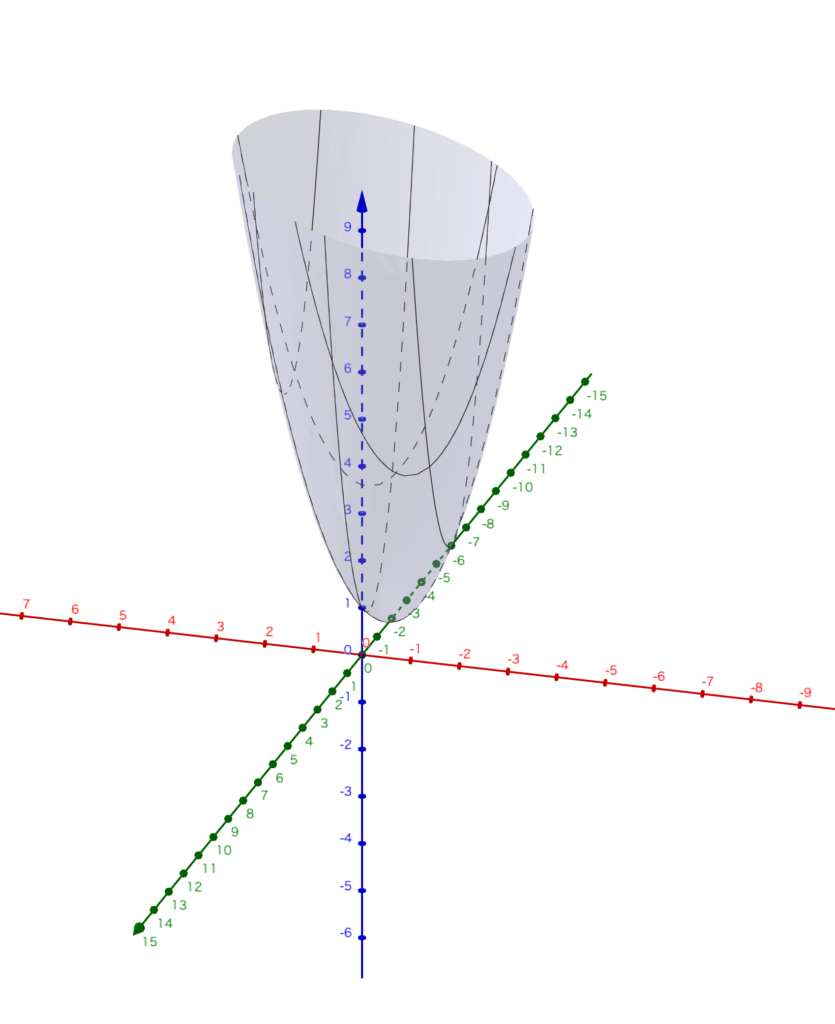
そこで\((a.b)=(0,0)\)として図で確かめてみましょう。
$$
{\rm grad}f(0,0)=
\left(
\begin{array}{c}
1\\
1
\end{array}
\right)
$$
です。
従って、点\((0,0)\)を\((1\ 1)\)の方向に動かしたときに\(f\)の値が最も変化します。

ただし、\(A=(0,0,1),\ B=(0,0,0),\ C=(1,1,0),\ D=(1,1,7)\)です。
確かに、めちゃめちゃ変化してますね。
例2. \(\displaystyle\boldsymbol{f}(x_1,x_2,x_3)=
\left(\begin{array}{c}
f_1(x_1,x_2,x_3)\\
f_2(x_1,x_2,x_3)
\end{array}\right)=
\left(\begin{array}{c}
x_1+2x_2+3x_3+7\\
4x_1+5x_2+6x_3+8
\end{array}\right)
\)
としたとき、\(\boldsymbol{f}\)のヤコビ行列を求めてみます。
\(\displaystyle\frac{\partial f_i}{\partial x_j}\)は定数関数ですので、\(\mathbb{R}^3\)で連続です。
従って、\(\boldsymbol{f}\)は\(\mathbb{R}^3\)で\(C^1\)級ですので全微分可能で、ヤコビ行列\(\displaystyle\boldsymbol{f}^\prime(x_1,x_2,x_3)=\left( \frac{\partial f_i}{\partial x_j}\right)\)は
$$
\left( \frac{\partial f_i}{\partial x_j}\right)=
\begin{pmatrix}
\displaystyle\frac{\partial f_1}{\partial x_1}&\displaystyle\frac{\partial f_1}{\partial x_2}&\displaystyle\frac{\partial f_1}{\partial x_3}\\
\displaystyle\frac{\partial f_2}{\partial x_1}&\displaystyle\frac{\partial f_2}{\partial x_2}&\displaystyle\frac{\partial f_2}{\partial x_3}\\
\end{pmatrix}
=
\begin{pmatrix}
1&2&3\\
4&5&6
\end{pmatrix}
$$
となります。
ちなみに、\(f_1\)の勾配ベクトル\({\rm grad}f_1\)は
$$
{\rm grad}f_1=\left(\begin{array}{c}
\displaystyle\frac{\partial f_1}{\partial x_1}\\
\displaystyle\frac{\partial f_1}{\partial x_2}\\
\displaystyle\frac{\partial f_1}{\partial x_3}\\
\end{array}\right)=
\left(\begin{array}{c}
1\\
2\\
3
\end{array}\right)
$$
で、
\(f_2\)の勾配ベクトル\({\rm grad}f_2\)は
$$
{\rm grad}f_1=\left(\begin{array}{c}
\displaystyle\frac{\partial f_2}{\partial x_1}\\
\displaystyle\frac{\partial f_2}{\partial x_2}\\
\displaystyle\frac{\partial f_2}{\partial x_3}\\
\end{array}\right)=
\left(\begin{array}{c}
4\\
5\\
6
\end{array}\right)
$$
です。
ベクトル値関数\(\boldsymbol{f}\)において、\(f_1\)は\((1\ 2\ 3)\)方向に点を動かすと最も\(f_1\)の値が変化し、\(f_2\)は\((4\ 5\ 6)\)方向に点を動かすと最も\(f_2\)の値が変化する、というわけです。
ベクトル値関数の場合は特に勾配はあまり気にしません。
結
今回は全微分に関連するヤコビ行列と勾配ベクトル(gradient)について解説しました。
あるベクトル値関数が全微分可能であるとき、全微分係数がヤコビ行列となります。
ベクトル値関数ではなく多変数実数値関数の場合はヤコビ行列の第1行目を転置したベクトルが勾配ベクトルとなります。
そして、勾配ベクトルは勾配ベクトルの方向に点を移動させたときに関数の値が最も変化する方向を指しています。
次回は多変数の合成関数の微分と逆関数の微分について解説します。
乞うご期待!質問、コメント等お待ちしております!





コメントをする