本記事の内容
本記事はラグランジュの未定乗数法を解説して、実際に条件付き極値問題を解いてみる、という記事です。
本記事を読むにあたり、陰関数定理について知っている必要があるため、以下の記事も合わせてご覧ください。
ラグランジュの未定乗数法って?
ラグランジュの未定乗数法は条件付き極値問題を解く手法であるのと同時に、極値に関する重要な事実です。
条件付き極値問題って?
では「条件付き極値問題って?」という話ですが、これは読んで字の如しで、ある関数にある条件を追加した場合の極値問題です。
今回は、2変数の場合に限って説明をします。
これまで扱った極値問題は、基本的に定義域が開集合でした。
すると、以下の定理が成り立つのでした。
定理1.(全微分可能な関数が内点で極値を取れば、全微分係数は\(0\)である。)
\(\Omega\)が\(\mathbb{R}^n\)の開集合、\(f:\Omega\to\mathbb{R}\)は全微分可能で、\(\boldsymbol{a}\in\Omega\)、\(f\)は\(\boldsymbol{a}\)で極大(または極小)ならば、\(f^\prime(\boldsymbol{a})=\boldsymbol{0}\)(これは\(\nabla f(\boldsymbol{a})=\boldsymbol{0}\)とも書ける)である。従って、極値点を探す、ということは比較的簡単でした。
これからは、関数\(f\)の極値を、条件
$$
g(x,y)=0
$$
という条件の下で考えます。
つまり、\(f\)を\(g\)の零点集合
$$
N_g=\{(x,y)|g(x,y)=0\}
$$
に制限したときの極値を求める、ということになります。
要するに、\(f:\Omega\to\mathbb{R}\)を\(N_g\)に制限した関数\(\left.f\right|_{N_g}:N_g\to\mathbb{R}\)について極値を求める、という話になります。
もし、\(N_g\)が開集合なのであれば、今までと同様に定理1.を使って極値を求めるわけですが、必ずしも\(N_g\)が開集合というわけではありません。
従って、\(f^\prime(\boldsymbol{a})=\boldsymbol{0}\)を満たす\(\boldsymbol{a}\)を探しても意味がありません。
どんな問題を考えるんですか?
例2. 方程式\(x+2y+3=0\)で表される平面内の曲線を\(L\)とします。
点\((x,y)\)が直線\(L\)上を動くときの、関数\(f(x,y)=x^2+y^2\)の最小値を求めてみましょう。
という問題です。
先述した\(g\)に対応するのは\(g(x,y)=x+2y+3\)です。
一応、これは原点と直線\(L\)との距離の平方になるだろうなあ、ということは直感的に分かるので、微分法を使わなくても解けますが後で、これをラグランジュの未定乗数法を使って求めます。
ラグランジュの未定乗数法
では2変数の場合のラグランジュの未定乗数法を明示して証明してみます。
ラグランジュの未定乗数法の明示
定理3. (2変数のラグランジュの未定乗数法)
\(\Omega\)を\(\mathbb{R}^2\)の開集合、\(f\)と\(g\)を\(\Omega\)で定められ、\(\mathbb{R}\)に値を持つ\(C^1\)級の関数として、 $$ N_g=\{(x,y)\in \Omega|g(x,y)=0\} $$ とおいたとき、 $$ \nabla g=\neq0\ {\rm on}\ N_g $$ が成り立つ。また、条件\(g(x,y)=0\)の下で、\(f\)は\(\boldsymbol{a}=\displaystyle\left(\begin{array}{c}\alpha\\ \beta\end{array}\right)\in N_g\)で極値を取るとする。すなわち、ちなみに、\(\lambda\)のことをラグランジュの未定乗数(Lagrange multiplier)といいます。
また、極値点の座標\(\alpha\)、\(\beta\)、未定定数\(\lambda\)は連立方程式
$$
\begin{cases}
g(\boldsymbol{a},\beta)=0\\
\displaystyle\frac{\partial f}{\partial x}(\alpha,\beta)=\lambda\frac{\partial g}{\partial x}(\alpha,\beta)\\
\displaystyle\frac{\partial f}{\partial y}(\alpha,\beta)=\lambda\frac{\partial g}{\partial y}(\alpha,\beta)\\
\end{cases}
$$
の解だ、と捉えることができるので、これから付帯的に求まる場合が多いです(未知数3個、方程式3個)。
この場合は、条件付き極値問題が解けるわけである。
この方法をラグランジュの未定乗数法と呼びます。
この条件は
$$
F(x,y,\lambda)=f(x,y)-\lambda g(x,y)
$$
とおくと、
$$
F_\lambda=F_x=F_y=0,\quad \nabla F=0
$$
と書けます。
この形で定理を述べている本も多いです。
いざ、証明
では、証明してみましょう!
ラグランジュの未定乗数法の証明
仮定
$$
\nabla g(\boldsymbol{a})\neq
\left(
\begin{array}{c}
0\\
0
\end{array}
\right)
$$
から、
$$
\frac{\partial g}{\partial x}(\boldsymbol{a})\neq0,\quad {\rm or}\quad \frac{\partial g}{\partial y}(\boldsymbol{a})\neq0
$$
です。
①\(\displaystyle\frac{\partial g}{\partial y}(\boldsymbol{a})\neq0\)の場合
ここで、陰関数定理を使います。
陰関数定理とは以下でした。
定理4.(陰関数定理、implicit function theorem)
\(\Omega\)は\(\mathbb{R}^m\times\mathbb{R}^n\)の開集合、\(\boldsymbol{F}:\Omega\ni(\boldsymbol{x},\boldsymbol{y})\mapsto \boldsymbol{F}(\boldsymbol{x},\boldsymbol{y})\in\mathbb{R}^n\)は\(C^1\)級、\((\boldsymbol{a},\boldsymbol{b})\in\Omega\)、\(\boldsymbol{F}(\boldsymbol{a},\boldsymbol{b})=\boldsymbol{0}\)、\(\displaystyle\det\left( \frac{\partial \boldsymbol{F}}{\partial \boldsymbol{y}}\right)(\boldsymbol{a},\boldsymbol{b})\neq\boldsymbol{0}\)が成り立つとする。このとき、\(\boldsymbol{a}\)を含む\(\mathbb{R}^m\)の開集合\(U\)、\(\boldsymbol{b}\)を含む\(\mathbb{R}^n\)の開集合\(V\)、\(C^1\)級の関数\(\boldsymbol{\varphi}:U\to V\)で、以下の1.,2.,3.,4.を満たすものが存在する。- \(U\times V\subset \Omega\).
- \(\boldsymbol{\varphi}(\boldsymbol{a})=\boldsymbol{b}\).
- \(\forall (\boldsymbol{x},\boldsymbol{y})\in U\times V\)に対して、\(\boldsymbol{F}(\boldsymbol{x},\boldsymbol{y})=\boldsymbol{0}\ \Longleftrightarrow\ \boldsymbol{y}=\boldsymbol{\varphi}(\boldsymbol{x})\).
- \(\forall \boldsymbol{x}\in U\)に対して、\(\displaystyle\boldsymbol{\varphi}^\prime(\boldsymbol{x})=-\left( \frac{\partial \boldsymbol{F}}{\partial \boldsymbol{y}}\left( \boldsymbol{x},\boldsymbol{\varphi}(\boldsymbol{x})\right)\right)^{-1}\frac{\partial \boldsymbol{F}}{\partial \boldsymbol{x}}\left( \boldsymbol{x},\boldsymbol{\varphi}(\boldsymbol{x})\right)\)
定理4.(陰関数定理)の証明は【解析学の基礎シリーズ】偏微分編 その13を御覧ください。
陰関数定理から、点\(\boldsymbol{a}\)の近傍で、
$$
g(x,y)=0\Longleftrightarrow y=\varphi(x)
$$
というように\(y\)について解けて、
$$
\varphi^\prime(x)=-\frac{\displaystyle\frac{\partial g}{\partial x}\left(x,\varphi(x)\right)}{\displaystyle\frac{\partial g}{\partial y}\left(x,\varphi(x)\right)}
$$
となります。
そこで、
$$
h(x)=f\left( x,\varphi(x)\right)
$$
とおくと、
\begin{eqnarray}
h^\prime(x)&=&\frac{\partial f}{\partial x}\left( x,\varphi(x)\right)+\frac{\partial f}{\partial y}\left( x,\varphi(x)\right)\varphi^\prime(x)\\
&=&\frac{\partial f}{\partial x}\left( x,\varphi(x)\right)+\frac{\partial f}{\partial y}\left( x,\varphi(x)\right)
\left(
-\frac{\displaystyle\frac{\partial g}{\partial x}\left(x,\varphi(x)\right)}{\displaystyle\frac{\partial g}{\partial y}\left(x,\varphi(x)\right)}
\right)
\end{eqnarray}
となります。
\(f\)は\(\boldsymbol{a}\)で極値を取るので、\(h(x)=f\left( x,\varphi(x)\right)\)は\(x=\alpha\)で極値を取ります。
従って、\(h^\prime(\alpha)=0\)、\(\left( \alpha,\varphi(\alpha)\right)=(\alpha,\beta)=\boldsymbol{a}\)に注意して、
$$
\frac{\partial f}{\partial x}(\boldsymbol{a})-\frac{\displaystyle\frac{\partial f}{\partial y}(\boldsymbol{a})}{\displaystyle\frac{\partial g}{\partial y}(\boldsymbol{a})}\cdot \frac{\partial g}{\partial x}(\boldsymbol{a})=0
$$
です。
さて、ここで、
$$
\lambda=\frac{\displaystyle\frac{\partial f}{\partial y}(\boldsymbol{a})}{\displaystyle\frac{\partial g}{\partial y}(\boldsymbol{a})}
$$
とおくと、すなわち
$$
\frac{\partial f}{\partial y}(\boldsymbol{a})-\lambda\frac{\partial g}{\partial y}(\boldsymbol{a})=0
$$
とおくと、
$$
\frac{\partial f}{\partial x}(\boldsymbol{a})-\lambda\frac{\partial g}{\partial x}(\boldsymbol{a})=0
$$
となります(計算すると分かります)。
さて、以上のことをまとめれば、
$$
\nabla f(\boldsymbol{a})=\lambda\nabla g(\boldsymbol{a})
$$
となります。
②\(\displaystyle\frac{\partial g}{\partial x}(\boldsymbol{a})\neq0\)のとき
この場合は\(g(x,y)=0\)に陰関数定理を適用させて\(x=\)の形に解いて、①と同じようにすれば証明できますので、省略します。
ラグランジュの未定乗数法の証明終わり
実際に計算してみよう!
例2.を解いてみましょう!
例2. 方程式\(x+2y+3=0\)で表される平面内の曲線を\(L\)とします。
点\((x,y)\)が直線\(L\)上を動くときの、関数\(f(x,y)=x^2+y^2\)の最小値を求めてみましょう。

①最小値が存在することの証明
正直、子の問題は図形的な意味が比較的分かりやすい部類だと思いますので、そういう意味では「最小値は存在するでしょ。ひと目見りゃ分かる。」となるわけですが、必ずしもこの問題のように図形的に、視覚的に分かりやすい問題ばかりではありません。
そこで、きちんと書くとどうなるか、ということを述べます。
\(L\)上の点\((x_0,y_0)\)を一つ取り、正の数\(R\)を\(R^2=x_0^2+y_0^2\)で定めて、\(D=\{(x,y)\in\mathbb{R}^2|x^2+y^2\leq R^2\}\)とおきます。
直線\(L\)を
$$
L=L\cap \mathbb{R}^2=L\cap(D\cup D^c)=(L\cap D)\cup (L\cap D^c)
$$
というように分解すると、\(L\cap D\)は\(\mathbb{R}^2\)の空でない有界閉集合なので、\(f\)は\(L\cap D\)において最小値\(m=f(\alpha,\beta)\)を持ちます。
ただし、ここで以下の事実を使いました。
定理5.(多次元版ワイエルシュトラスの最大値定理)
\(K\)は\(\mathbb{R}^n\)の空でない有界な閉集合であり、\(f:K\to\mathbb{R}\)は\(K\)で連続であるとする。このとき、\(f\)は最大値を持つ。すなわち、 $$ (\exists \boldsymbol{c}\in K)\ (\forall \boldsymbol{x}\in K)\ f(\boldsymbol{c})\geq f(\boldsymbol{x}) $$ が成り立つ。 最小値についても同様である。定理5.の証明は【解析学の基礎シリーズ】多変数関数編 その18を御覧ください。
ところで、\((\alpha,\beta)\in D\)なのだから、\(m=f(\alpha,\beta)=\alpha^2+\beta^2\leq R^2\)を満たしています。
一方で、\(L\cap D^c\)においては、\(f(x,y)=x^2+y^2>R\)だから、\(m\)は\(f\)の\(L\)全体における最小値です。
従って、最小値が存在することが示されました。
②唯一の極値は最小値
①で最小値が存在することが分かりましたが、最小値は極値ですので、もしその極値が1つしか無いのであれば、それが最小値に他なりません。
③\(f\)の条件付き極値を求める。
関数\(g:\mathbb{R}^2\to\mathbb{R}\)を\(g(x,y)=x+2y+3\)で定めると、
$$
\nabla g(x,y)=
\left(
\begin{array}{c}
1\\
2
\end{array}
\right)\neq\boldsymbol{0}
$$
です。
従って、条件\(g(x,y)=0\)の下での\(f\)の極値点は、もし存在すれば、ラグランジュの未定乗数法でも止まります。
では、未定定数を\(\lambda\)とおくと
\begin{eqnarray}
&&f_x(x,y)-\lambda g_x(x,y)=0,\\
&&f_y(x,y)-\lambda g_y(x,y)=0,\\
&&g(x,y)=0
\end{eqnarray}
を満たす\(x\)、\(y\)、\(\lambda\)が求めたいもので、\(f\)はこの連立方程式の解\((x,y)\)で極値を取りうる、ということになります。
従って、
\begin{eqnarray}
&&2x-\lambda=0,\\
&&2y-2\lambda=0,\\
&&x+2y+3=0
\end{eqnarray}
の解を知りたいわけです。
これを解くと、
$$
\lambda=-\frac{6}{5},\quad x=-\frac{3}{5},\quad y=-\frac{6}{5}
$$
となり、ただ一つだけです。
実は、このようにラグランジュの未定乗数法で求められた点が極値点であるかどうかは一般にはすぐは分かりません。
しかもラグランジュの未定乗数法は「極値を取れば」という条件が課されているため、ラグランジュの未定乗数法で求めた点が極値点であるかどうかを議論しなければなりません。
そのために、以前解説したヘシアンやらを使うのです。
しかし、ここでは既に最小値が存在することが示されていて、最小値たりえる点の候補がただ1つなので、\(f\)は\(\displaystyle(x,y)=\left( -\frac{3}{5},-\frac{6}{5}\right)\)で極小値を取り、さらにこれは同時に最小値です。
以上をまとめると、\(f\)は\(\displaystyle(x,y)=\left( -\frac{3}{5},-\frac{6}{5}\right)\)で最小値
$$
f\left( -\frac{3}{5},-\frac{6}{5}\right)=\frac{9}{5}
$$
を取ります。
ラグランジュの未定乗数法のキモチの部分
ラグランジュの未定乗数法のキモチの部分を解説します。
再度条件付き極値問題とはどういう問題かということを明示しておきます。
このとき、\(g(x,y)=0\)を制約条件と呼び、\(f(x,y)\)を目的関数と呼びます。
これを図で説明するとこんな感じです。

この限られた範囲(範囲というと領域のような感じですが、制約条件は直線だったりすることもあります。例2.がまさにそうですよね)。
では、次に図形的意味を解説しようと思います。
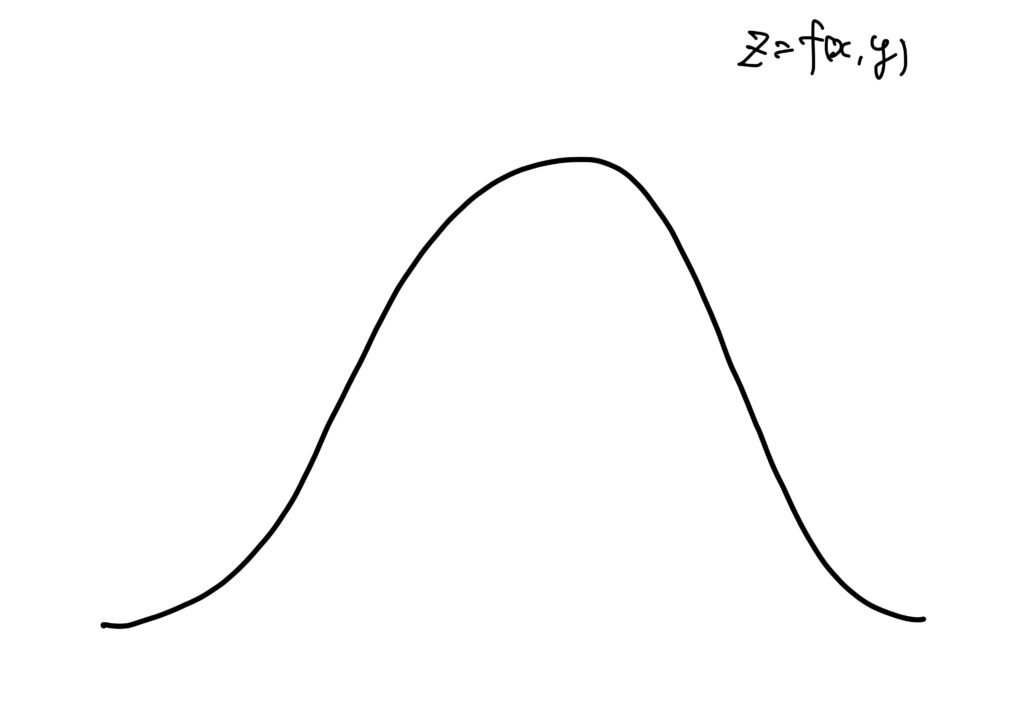
仮に\(z=f(x,y)\)が下のような形の曲面だったとしましょう。
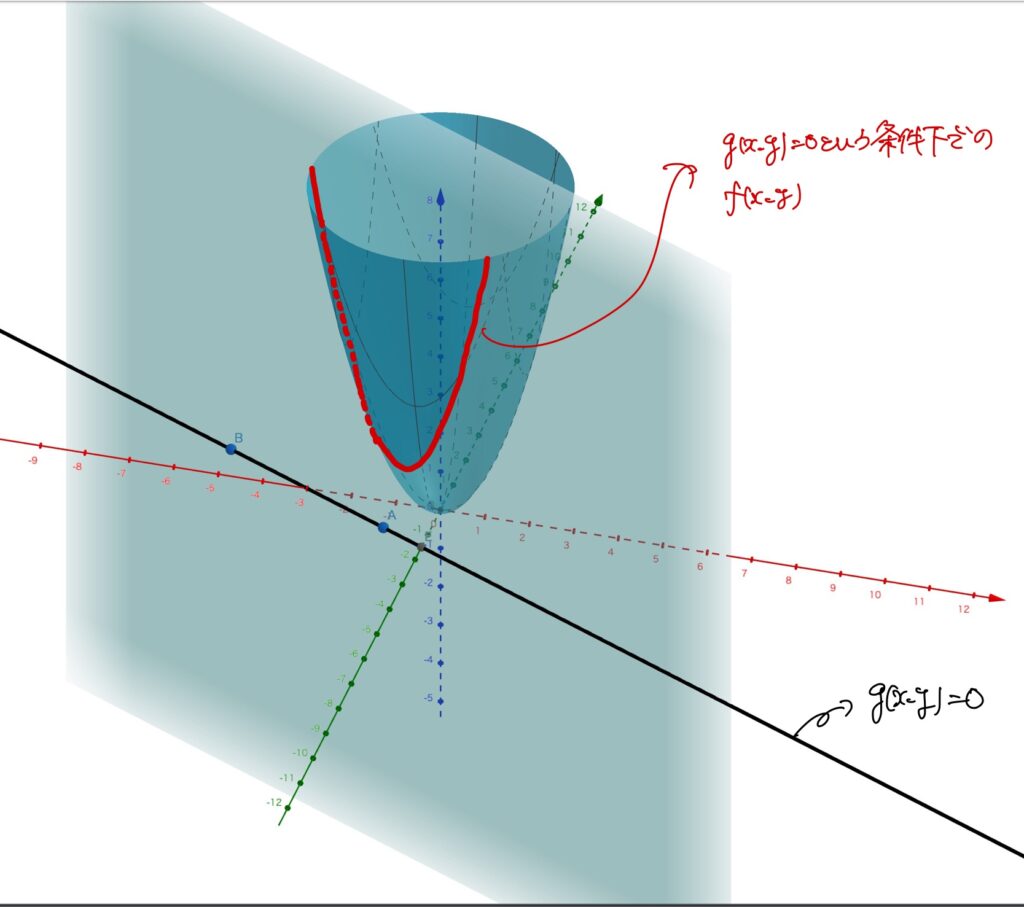
このとき、制約条件\(g(x,y)=0\)を満たすような\(f\)が以下のような曲面だったとしましょう。
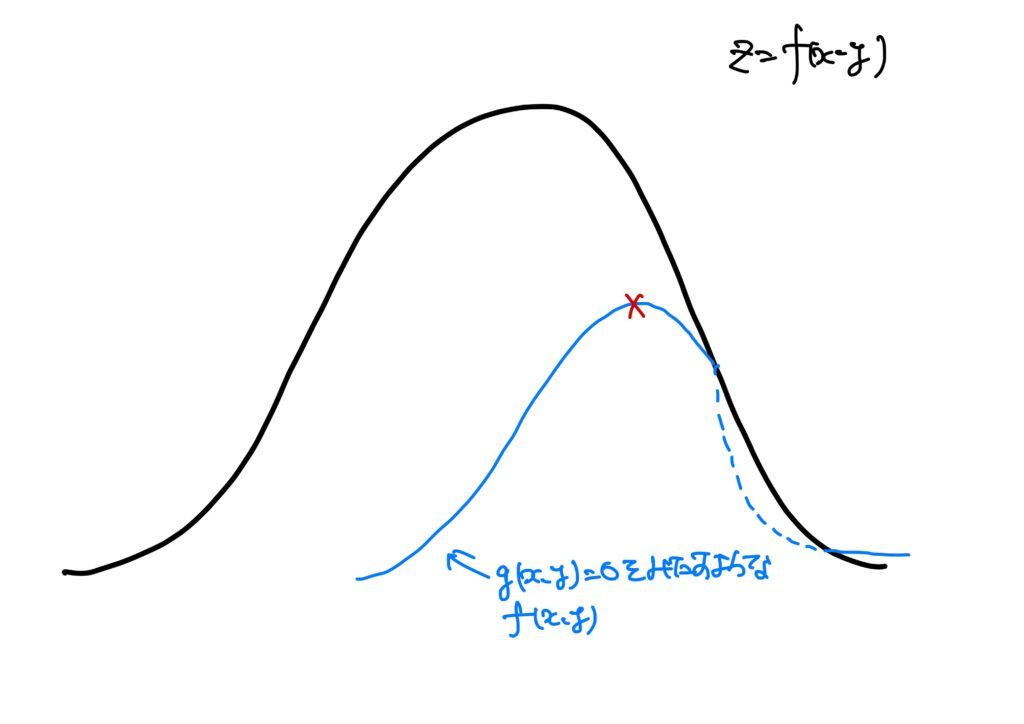
これを見ると、条件付き極大値と極小値は印をつけたところだろうな、とイメージが湧くと思います。
さて、これを等高線で切ってみます。
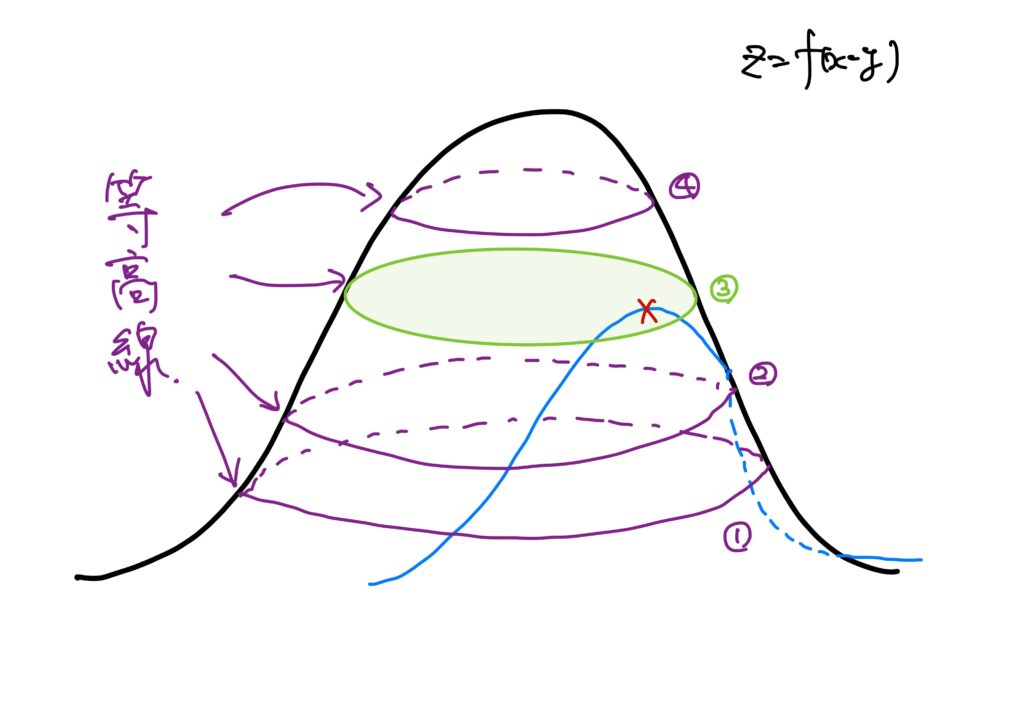
この等高線を描いた図を真上から見てみると、以下のように見えます。
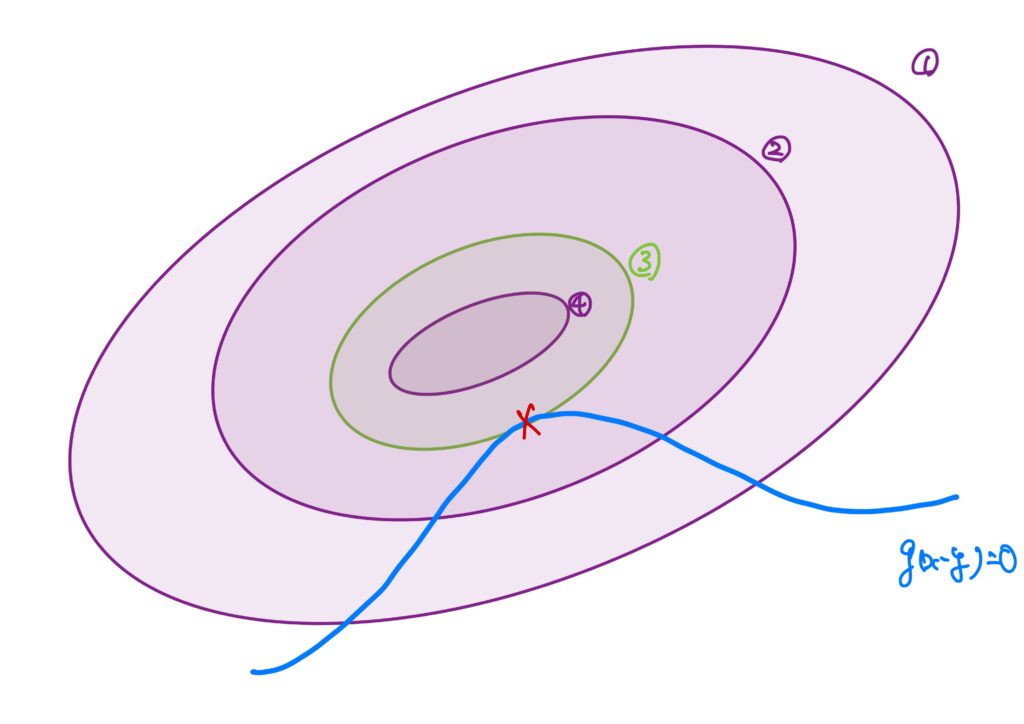
このとき、条件付き極大は、等高線が先程の図で印を付けた部分と接するときに極大を取ります。
これを数学的に表現しましょう。
今、”接する”と言っているわけですので、これは”接線を共有している”と言い換えることができます。
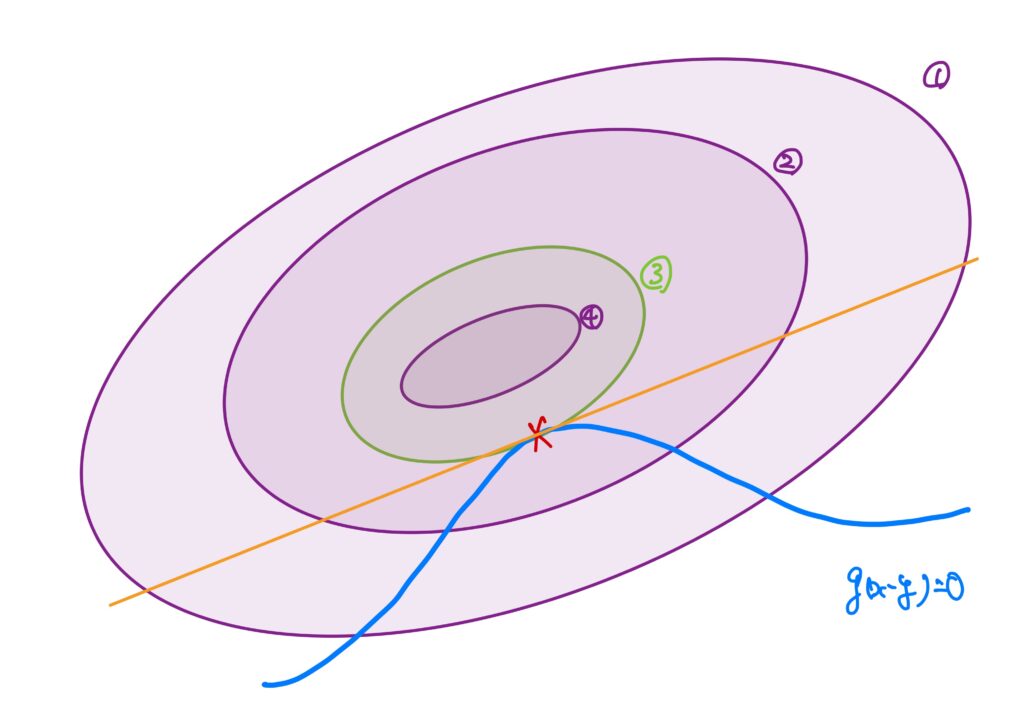
これを別の言い方をすると、「その点における勾配\(\nabla f\)と直交するような直線が接線である」ということです。

勿論、このとき\(g\)についても勾配\(\nabla g\)を考える事ができます。
そのベクトルは以下です。
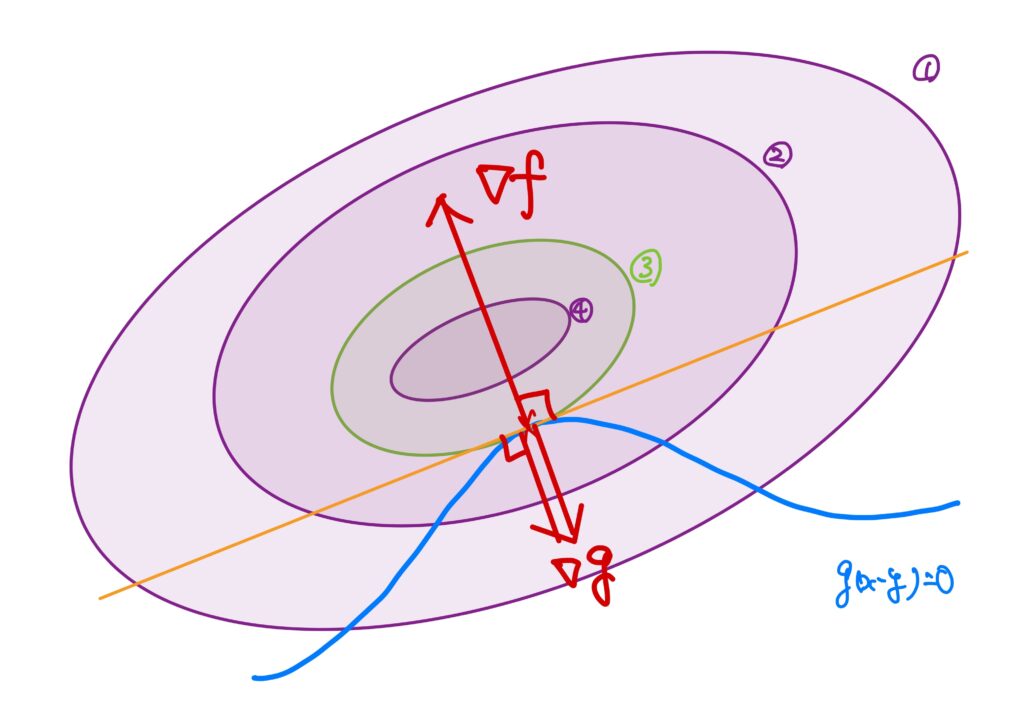
ここで、”接線を共有している”わけですので、大きさに違いはあれど、\(\nabla f\)と\(\nabla g\)は同一直線上にあるはずです。
従って、
$$
\nabla f=\lambda \nabla g
$$
という式が出現するのです。
そして勿論\(g(x,y)=0\)という条件も出現します。
こういう背景だったわけです。
読者の皆様のコメントを下さい!
今回もクイズを出題したいなと思います。
大丈夫。なんてことありません。
ちょっとした余暇にでも考えてくだされば嬉しいです。
ちょいと引用します。
前には危険 後ろは安全
君が見つけさえすれば2つが君を救うだろう
7つのうちの1つだけ 君を前進させるだろう
別の1つで退却の道が開ける その人に2つの瓶はイラクサ酒
残る3つは殺人者 列にまぎれて隠れてる
長々居たくないならば どれかを選んでみるがいい
君が選ぶのに役に立つ 4つのヒントを差し上げようまず第1のヒントだが どんなにずるく隠れても
毒入り瓶のある場所は いつもイラクサ酒の左第2のヒントは両端の 2つの瓶は種類が違う
君が前進したいなら 2つのどちらも友ではない第3のヒントは見たとおり 7つの瓶は大きさが違う
小人も巨人もどちらにも 死の毒薬は入ってない第4のヒントは双子の薬 ちょっと見た目は違っても
引用:J. K. ローリング著、松岡祐子訳「ハリー・ポッターと賢者の石」より
左端から2番目と 右の端から2番目の 瓶の中身は同じ味
※小人と巨人は一番小さい瓶と一番大きい瓶を指しています。
そして、置いてあるとしましょう。
図を挿入
この中で前進するための薬はどれでしょうか?
是非コメントで解答をお待ちしています!
結
今回はラグランジュの未定乗数法について解説しました。
ラグランジュの未定乗数法は条件付き極値問題を考える手法であるのと同時に重要な事実です。
筆者の印象ですが、極値問題は、全定義域での話よりも「この条件下で」という制約条件の下での極値問題の方が多い印象があります。
さて、今回で偏微分編はおしまいです。
次回からは重積分の話に入ります。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!




コメントをする