「偏微分？」「高階微分？」「$C^k$級？」【解析学の基礎シリーズ】偏微分編その1

本記事の内容
多変数関数の微分のちょっとしたイントロ①
多変数関数の微分のちょっとしたイントロ②(微分から偏微分へ)
で、偏微分って何スか？
1. 偏微分
2. で、結局偏微分って何なんですか？
偏導関数、高階微分、 $C^k$ 級
いっちょ偏微分可能であることを証明してみっか。
結

本記事の内容

本記事は偏微分、高階偏微分、 $C^k$ 級について解説する記事です。

本記事を読むにあたり、１変数関数の微分と多変数関数の極限について知っている必要があるため、以下の記事も合わせてご覧ください。

※シリーズ化しているので、シリーズの一部の記事のリンクを掲載しています。

↓多変数関数の極限の記事

多変数関数の微分のちょっとしたイントロ①

１変数実数値関数と同様にして、多変数関数にも微分法を考えます。
むしろ、多変数関数の微分法を考えることのほうが多い印象があります。
というのも、1変数実数値関数 $f: \mathbb{R}\to\mathbb{R}$ というのは、何か1つの実数 $x$ に対して、実数 $f(x)$ を対応させる写像のことなので、値が $x$ にしか依存しません。
つまり、何か１つの対象が変数 $x$ にしか縛られない、ということで $x$ さえ分かってしまえば対象が何であるか確定する、ということになります。

しかし、現実はそう単純ではありません。
例えば、インクを水に垂らしたときに、そのインクが水の中でどんどん広がっていく現象を記述したりする方程式を拡散方程式といいますが、拡散方程式は変数が複数存在する微分方程式(微分が含まれる方程式)です。
ちなみに、拡散方程式は花粉の広がり方などに使われたりもします。

他には、流体中の粒子の運動を記述したNavier-Stokes方程式も変数が複数存在する微分方程式(これを偏微分方程式といいます)です。

(※ちなみに、Navier-Stokes方程式はNewtonの古典力学の運動方程式を流体力学版へと改変したものです。つまり、Navier-Stokes方程式も運動方程式です。)

このように、実は変数がただ１つだけの方程式よりも複数存在する方程式の方がより多く出現します(と断言してしまうのはマズいかもしれないけれど、筆者はそういう印象です)。

余談

ちなみに…Navier-Stokes方程式はNewtonの古典力学の運動方程式を流体力学版へと改変したものです。
つまり、Navier-Stokes方程式も運動方程式です。

少々筆者のパーソナルな話になってしまいますが、高校生のときの筆者が進学する大学を選ぶときに、「世の中の現象を数式で表せるなんて凄い！面白そう！これがやりたい！」と思って大学を選びました。
とはいえ、実際やってみたらより純粋な数学のほうが面白くなってしまって専門にはしませんでしてけれどね(笑)

多変数関数の微分のちょっとしたイントロ②(微分から偏微分へ)

１変数の微分から多変数の微分についての橋渡しをしたいと思います(うまくできるかな…)。

１変数の微分法のチャラい復習

微分可能、微分係数

$I=(a,b)$ を

$\mathbb{R}$ の開区間とし、

$f:I\to \mathbb{R}$ とする。このとき、

$t\in I$ に対して

$c=\lim_{h\to 0}\frac{f(t+h)-f(t)}{h}$ という

$c\in \mathbb{R}$ が存在するとき、

$f$ は

$t$ で微分可能であるといい、

$c$ を

$f$ の導値、または微分係数という。このとき、

$c=f^\prime(t)=\frac{df}{dt}(t)=\frac{d}{dt}f(t)=\frac{df(t)}{dt}=\left(f(t)\right)^\prime=\left(Df\right)(t)$ と書く。

でした。
詳しくは【解析学の基礎シリーズ】１変数実数値関数の微分編その1を御覧ください。

偏微分のイントロ+全微分との関係

多変数の場合だと、変化量 $h$ は実数ではなくベクトルになります。
従って、このままでは使えません。

実は、多変数関数には微分が２種類存在します。

全微分 $f^\prime(a)$
偏微分 $\displaystyle\frac{\partial f}{\partial x_j}(a)$

実は、１変数の微分 $f^\prime(a)$ とよく対応するのは、全微分の方です(それ故同じ記号を使っています)。

例えば、１変数実数値関数 $f$ のグラフ $y=f(x)$ 上の点 $(a,f(a))$ における接線の方程式は
$y=f^\prime(a)(x-a)+f(a)$
ですが、多変数実数値関数 $f$ のグラフ $y=f(\boldsymbol{x})$ 上の点 $(a,f(\boldsymbol{a}))$ においては接線ではなく接平面になります。
その方程式は
$y=f^\prime(\boldsymbol{a})(\boldsymbol{x}-\boldsymbol{a})+f(\boldsymbol{a})$
です。
形式的には違いはなくて、覚えるという意味では苦労がほぼ無いと思います。

また、 $f$ がベクトル値 $\displaystyle\boldsymbol{f}= \left( \begin{array}{c} f_1\\ f_2\\ \vdots\\ f_m \end{array} \right)$ の場合、
$\frac{\partial \boldsymbol{f}}{\partial x_j}(a)= \left( \begin{array}{c} \displaystyle\frac{\partial f_1}{\partial x_j}(a)\\ \displaystyle\frac{\partial f_2}{\partial x_j}(a)\\ \vdots\\ \displaystyle\frac{\partial f_m}{\partial x_j}(a)\\ \end{array} \right)$
となります。

全微分の偏微分の関係性はある種、簡単です。

$\begin{eqnarray} \boldsymbol{f}^\prime(a)&=&\left( \frac{\partial \boldsymbol{f}}{\partial x_1}(a)\ \frac{\partial \boldsymbol{f}}{\partial x_2}(a)\ \cdots\ \frac{\partial \boldsymbol{f}}{\partial x_n}(a)\ \right)\\ &=& \begin{pmatrix} \displaystyle\frac{\partial f_1}{\partial x_1}(a)&\displaystyle\frac{\partial f_1}{\partial x_2}(a)&\cdots &\displaystyle\frac{\partial f_1}{\partial x_n}(a)\\ \displaystyle\frac{\partial f_2}{\partial x_1}(a)&\displaystyle\frac{\partial f_2}{\partial x_2}(a)&\cdots &\displaystyle\frac{\partial f_2}{\partial x_n}(a)\\ \vdots&\vdots& \ddots&\vdots\\ \displaystyle\frac{\partial f_m}{\partial x_1}(a)&\displaystyle\frac{\partial f_m}{\partial x_2}(a)&\cdots &\displaystyle\frac{\partial f_m}{\partial x_n}(a)\\ \end{pmatrix}= \left(\frac{\partial f_i}{\partial x_j}(a) \right) \end{eqnarray}$
です。
つまり、

全微分係数は偏微分係数を成分とする行列のこと。

です。

要するに、今までの１変数実数値関数の微分係数は接線の傾きだったのに対して、多変数の場合は接平面の傾きに対応する、ということです。
そして、多変数の微分も結局の所は１変数の微分と形式的にはさして変わらないぜということです。

直感的な偏微分のイメージ

本質的に１変数の場合と何が違うか、というと、１変数の場合は微分に方向が１つしかありませんでした。
というのも変数が1つだったからです。
しかしながら、多変数の場合は方向が複数あります。
例えば2変数だったとすると、 $x$ 方向(横の方向)と $y$ 方向(奥行きの方向)の２つの方向があります。
それ故、 $x$ で微分する、 $y$ で微分する、ということになるのです。

先程の記号 $\displaystyle\frac{\partial f}{\partial x}$ と $\frac{\partial f}{\partial y}$ はそれぞれ $x$ 方向の $f$ の変化量、 $y$ 方向の $f$ の変化量を表しています。

で、偏微分って何スか？

「偏微分とはこれです！」と言いたいところですが、まずは例を挙げます。

偏微分

例1.(2変数2次関数) 実定数 $a,,b,c,d,p,q,r\in\mathbb{R}$ に対して、
$f(x,y)=ax^2+bxy+cy^2px+qy+r\quad ((x,y)\in\mathbb{R}^2)$
として、 $f:\mathbb{R}^2\to\mathbb{R}$ を定めるとき、
$\frac{\partial f}{\partial x}=2ax+by+p$
です。

「おいおい。偏微分についてまだ何も言ってないのにいきなりヘンチクリンな記号を使って書かれたってわかんねんよ。」となると思いますが、大丈夫です。
後でしっかり解説しますが、ここでは1変数関数の $x$ での微分を $\displaystyle\frac{df}{dx}$ と書いたのに対して、多変数関数の $x$ での微分を $\frac{\partial f}{\partial x}$ と書いた、と思ってくれてOKです。

多変数関数に対して、ある１つの変数 $x$ で微分することを $x$ で偏微分する、といいますが、偏微分する際は他の変数(今回は $y$ )を定数とみなして微分します。
同様にして
$\begin{eqnarray} \frac{\partial f}{\partial y}&=&bx+2cy+q\\ \frac{\partial^2 f}{\partial x^2}&=&\frac{\partial }{\partial x}\left( \frac{\partial f}{\partial x}\right)=2a\\ \frac{\partial^2 f}{\partial y\partial x}&=&\frac{\partial }{\partial y}\left( \frac{\partial f}{\partial x}\right)=b\\ \frac{\partial^2 f}{\partial x\partial y}&=&\frac{\partial }{\partial x}\left( \frac{\partial f}{\partial y}\right)=b\\ \frac{\partial^2 f}{\partial y^2}&=&\frac{\partial }{\partial y}\left( \frac{\partial f}{\partial y}\right)=2c\\ \end{eqnarray}$
です。

ちなみに、 $f$ の全微分 $f^\prime(x,y)$ は
$f^\prime(x,y)=\left( \frac{\partial f}{\partial x}\ \frac{\partial f}{\partial y}\right)=\left(2ax+by+p\ bc+2cy+q \right)$
となります。
しかし、これは $\displaystyle \left( \begin{array}{c} 2ax+by+p\\ bc+2cy+q \end{array}\right)$
ではありません。
これは $\nabla f(x,y)$ という記号で表されます。

で、結局偏微分って何なんですか？

そんな怒らないでくださいよ。ちゃんと説明しますから。

偏微分可能、偏微分係数

$\Omega$ は

$\mathbb{R}^n$ の開集合、

$\boldsymbol{f}:\Omega\to\mathbb{R}^m$ 、

$\boldsymbol{a}=\left( \begin{array}{c} a_1\\ \vdots\\ a_n \end{array}\right)\in\Omega$ 、

$j=\{1,\dots,n\}$ とする。

$\boldsymbol{f}$ が点

$\boldsymbol{a}$ で変数

$x_j$ について偏微分可能であるとは、極限

$\lim_{h\to0}\frac{\boldsymbol{f}(\boldsymbol{a}+h\boldsymbol{e}_j)-\boldsymbol{f}(\boldsymbol{a})}{h}$ が存在することを言う。ただし、

$\boldsymbol{e}_j$ は第

$j$ 成分が

$1$ で、それ以外の成分すべて

$0$ であるような

$\mathbb{R}^n$ のベクトルとする。すなわち、

$\boldsymbol{e}_j= \left( \begin{array}{c} 0\\ \vdots\\ 0\\ 1\\ 0\\ \vdots\\ 0 \end{array}\right) \begin{array}{c} \\ \\ \\ \leftarrow j番目\\ \\ \\ \\ \end{array}$ である。
　このとき、極限値

$\in\mathbb{R}^m$ を

$\boldsymbol{f}$ の点

$\boldsymbol{a}$ での変数

$x_j$ についての偏微分係数(the partial derivative of

$f$ in the direction

$x_j$ at

$\boldsymbol{a}$ )と呼び、

$\frac{\partial \boldsymbol{f}}{\partial x_j}(a),\quad\frac{\partial }{\partial x_j}\boldsymbol{f}(a),\quad \boldsymbol{f}_{x_j}(a)$ などの記号で表す。

さて、上記の
$\frac{\boldsymbol{f}(\boldsymbol{a}+h\boldsymbol{e}_j)-\boldsymbol{f}(\boldsymbol{a})}{h}$
をベクトルの記法を使わずに成分でもって表すと、
$\begin{eqnarray} &&\frac{\boldsymbol{f}(\boldsymbol{a}+h\boldsymbol{e}_j)-\boldsymbol{f}(\boldsymbol{a})}{h}\\ &=& \frac{\boldsymbol{f}(a_1,\dots,a_{j-1},\color{red}{a_j+h},a_{j+1},\dots.a_n)-\boldsymbol{f}(a_1,\dots,a_{j-1},a_j,a_{j+1},\dots.a_n)}{h} \end{eqnarray}$
となります。

偏導関数、高階微分、 $C^k$ 級

１変数実数値関数と同様にして、高階微分、 $C^k$ 級というコンセプトが定まります。

偏導関数、高階微分、 $C^k$ 級

$\Omega$ は

$\mathbb{R}^n$ の開集合、

$\boldsymbol{f}:\Omega\to\mathbb{R}^m$ とする。

偏微分可能

$j\in\{1,\dots,n\}$

$\boldsymbol{f}$

$\Omega$

$x_j$

偏微分可能

$\forall \boldsymbol{x}\in\Omega$

$\boldsymbol{f}$

$\boldsymbol{x}$

$x_j$

$\Omega\ni \boldsymbol{x}\mapsto \frac{\partial \boldsymbol{f}}{\partial x_j}(\boldsymbol{x})\in\mathbb{R}^m$

$\boldsymbol{f}$

$x_j$

偏導関数

$\frac{\partial \boldsymbol{f}}{\partial x_j},\quad \frac{\partial }{\partial x_j}\boldsymbol{f},\quad \boldsymbol{f}_{x_j}$

1階偏導関数

$\displaystyle\frac{\partial \boldsymbol{f}}{\partial x_1},\cdots,\frac{\partial \boldsymbol{f}}{\partial x_n}$

$\boldsymbol{f}$

1階偏導関数

記号

$i,j\in\{1,\dots,n\}$

$\boldsymbol{f}$

$\Omega$

$x_j$

$\displaystyle\frac{\partial \boldsymbol{f}}{\partial x_j}$

$\Omega$

$x_j$

$\displaystyle\frac{\partial }{\partial x_j}\left( \frac{\partial \boldsymbol{f}}{\partial x_j}\right)$

$\frac{\partial^2 \boldsymbol{f}}{\partial x_i\partial x_j},\quad \boldsymbol{f}_{x_jx_i}$

$i=j$

$\displaystyle\frac{\partial^2 \boldsymbol{f}}{\partial x_j\partial x_j}$

$\displaystyle\frac{\partial^2 \boldsymbol{f}}{\partial x_j^2}$

2階偏導関数

$\displaystyle\frac{\partial^2 \boldsymbol{f}}{\partial x_i\partial x_j}\ (i,j=1,\cdots,n)$

$\boldsymbol{f}$

2階偏導関数

$k$ 階偏導関数

$k\in\mathbb{N}\ (k\geq3)$

$\boldsymbol{f}$

$k$ 階偏導関数

$C^k$ 級

$k\in\mathbb{N}$

$\boldsymbol{f}$

$\Omega$

$C^k$

$\boldsymbol{f}$

$\Omega$

$k$

$\boldsymbol{f}$

$\Omega$

$C^\infty$ 級

$\boldsymbol{f}$

$\Omega$

$C^\infty$

$\forall k\in\mathbb{N}$

$\boldsymbol{f}$

$\Omega$

$C^k$

$C^0$ 級

$\boldsymbol{f}$

$\Omega$

$C^0$

$\boldsymbol{f}$

$\Omega$

$\boldsymbol{f}$

$0$

いやあ。長い。長かった。
しかしながら、読んでみると、「ああ、１変数のときと同じじゃんね」となったかと思います。
強いて言えば、多変数ベクトル値関数の極限を知っている必要がありますが、これについてはすでに学んでいるので大丈夫かと思います。

ちなみに、チャラく復習すると、以下でした。

多変数ベクトル値関数の収束

$\Omega\subset\mathbb{R}^n$ を

$\mathbb{R}^n$ の領域、

$\boldsymbol{f}:\Omega\to\mathbb{R}^m$ を写像(関数)、

$\boldsymbol{a}\in\bar{\Omega}$ 、

$\boldsymbol{A}\in\mathbb{R}^m$ とする。

$\boldsymbol{x}\to\boldsymbol{a}$ のとき

$f(\boldsymbol{x})$ が $\boldsymbol{A}$ に収束する(このことを

$\boldsymbol{f}(\boldsymbol{x})\to \boldsymbol{A}\ (\boldsymbol{x}\to \boldsymbol{a})$ と表す)とは、

$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall \boldsymbol{x}\in\bar{\Omega}:0<|\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow |\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{A}|<\epsilon)$ が成り立つことをいう。

$\boldsymbol{A}$ のことを

$\boldsymbol{x}\to \boldsymbol{a}$ のときの

$\boldsymbol{f}(\boldsymbol{x})$ の極限と呼び、

$\displaystyle\lim_{\boldsymbol{x}\to \boldsymbol{a}}\boldsymbol{f}(\boldsymbol{x})=\boldsymbol{A}$ と表す。また、

$\boldsymbol{x}\to \boldsymbol{a}$ のときに

$\boldsymbol{f}(\boldsymbol{x})$ が極限を持つ(あるいは「

$\boldsymbol{f}(\boldsymbol{x})$ が収束する」)とは、ある

$\boldsymbol{A}\in\mathbb{R}^m$ が存在して、

$\boldsymbol{x}\to \boldsymbol{a}$ のときに

$\boldsymbol{f}(\boldsymbol{x})$ が

$\boldsymbol{A}$ に収束することをいう。

また、多変数ベクトル値関数の連続は以下でした。

多変数ベクトル値関数の連続

$\Omega$ を

$\mathbb{R}^n$ の領域、

$\boldsymbol{f}:\Omegaと\to\mathbb{R}^m$ とする。

$\boldsymbol{a}\in\Omega$ とする。 $\boldsymbol{f}$ が $\boldsymbol{a}\in\Omega$ で連続(continuous at $\boldsymbol{a}$ )であるとは、 $\lim_{\boldsymbol{x}\to\boldsymbol{a}}\boldsymbol{f}(\boldsymbol{x})=\boldsymbol{f}(\boldsymbol{a})$ が成り立つことをいう。

$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall\boldsymbol{x}\in\Omega;\ 0<|\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow |\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{f}(\boldsymbol{a})|<\epsilon)$

$\boldsymbol{f}$ が $\Omega$ で連続である(continuous on $\Omega$ )とは、任意の $\boldsymbol{a}\in \Omega$ に対して、 $\boldsymbol{f}$ が $\boldsymbol{a}$ で連続であることをいう。

$(\forall \boldsymbol{a}\in\Omega)(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall \boldsymbol{x}\in\Omega:\ 0<|\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow |\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{f}(\boldsymbol{a})|<\epsilon)$

いっちょ偏微分可能であることを証明してみっか。

してみましょう。

例2. $\displaystyle f(x,y)= \begin{cases} \displaystyle\frac{xy}{x^2+y^2}&((x,y)\neq(0,0))\\ 0&((x,y)=(0,0))\\ \end{cases}$ とします。

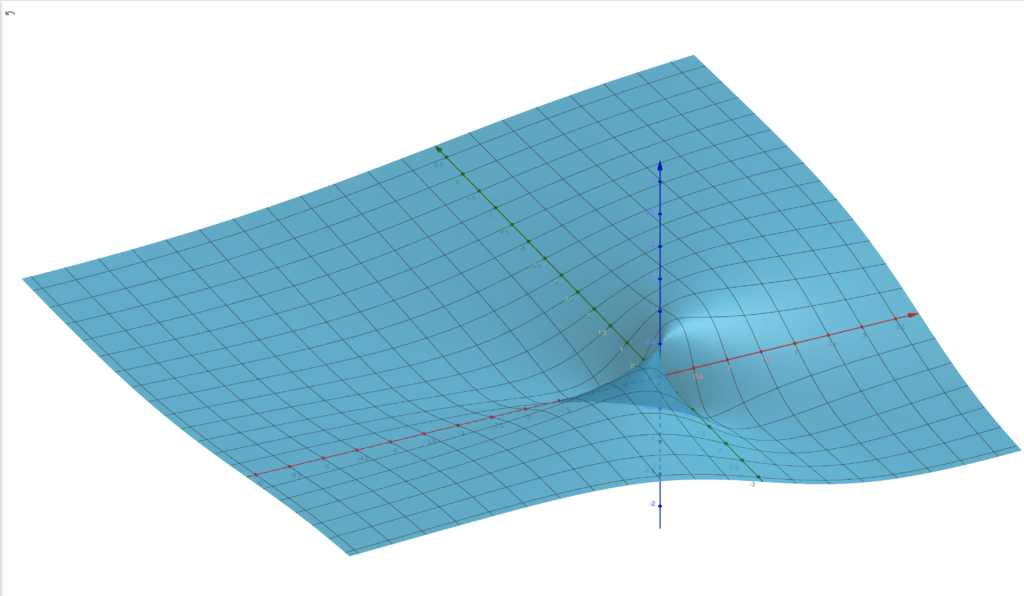
このとき、 $f$ が原点 $O=(0,0)$ で偏微分可能であるかを調べてみます(まあ、偏微分可能なんですけどね)。

まず、 $f$ が原点で $x$ で偏微分可能であるかを調べてみます。

$\begin{eqnarray} \lim_{h\to0}\frac{f((0,0)+h(1,0))-f(0,0)}{h}&=&\lim_{h\to0}\frac{f(h,0)-f(0,0)}{h}\\ &=&\lim_{h\to0}\frac{1}{h}\left(\frac{h\cdot0}{h^2+0^2}-f(0,0)\right)\\ &=&\lim_{h\to0}\frac{1}{h}\left(\frac{0}{h^2+y^2}-0\right)=0 \end{eqnarray}$
従って、極限が存在するので、 $f$ は原点で $x$ で偏微分可能です。

同様にして、
$\begin{eqnarray} \lim_{h\to0}\frac{f((0,0)+h(0,1))-f(0,0)}{h}&=&\lim_{h\to0}\frac{f(0,h)-f(0,0)}{h}\\ &=&\lim_{h\to0}\frac{1}{h}\left(\frac{h\cdot0}{0^2+h^2}-f(0,0)\right)\\ &=&\lim_{h\to0}\frac{1}{h}\left(\frac{0}{0^2+h^2}-0\right)=0 \end{eqnarray}$
となるので、 $f$ は原点で $y$ で偏微分可能です。

例3. $\displaystyle f(x,y)= \begin{cases} \displaystyle\frac{x}{x^2+y^2}&((x,y)\neq(0,0))\\ 0&((x,y)=(0,0))\\ \end{cases}$ とします。

このとき、 $f$ が $(0,0)$ で偏微分可能かを考えてみます。

まず、 $f$ が原点で $x$ で偏微分可能であるかを調べてみます。

$\begin{eqnarray} \lim_{h\to0}\frac{f((0,0)+h(1,0))-f(0,0)}{h}&=&\lim_{h\to0}\frac{f(h,0)-f(0,0)}{h}\\ &=&\lim_{h\to0}\frac{1}{h}\left(\frac{h}{h^2+0^2}-f(0,0)\right)\\ &=&\lim_{h\to0}\frac{1}{h}\left(\frac{h}{h^2}-0\right)\\ &=&\lim_{h\to0}\frac{1}{h}\cdot\frac{h}{h^2}\\ &=&\lim_{h\to0}\frac{1}{h^2}=\infty \end{eqnarray}$
従って、極限が存在しないので、 $f$ は原点で $x$ で偏微分可能ではありません。

同様にして、

$\begin{eqnarray} \lim_{h\to0}\frac{f((0,0)+h(0,1))-f(0,0)}{h}&=&\lim_{h\to0}\frac{f(0,h)-f(0,0)}{h}\\ &=&\lim_{h\to0}\frac{1}{h}\left(\frac{0}{0^2+h^2}-f(0,0)\right)\\ &=&\lim_{h\to0}\frac{1}{h}\left(0-0\right)=0 \end{eqnarray}$
従って、極限が存在するので、 $f$ は原点で $y$ で偏微分可能です。

結

今回は、偏微分、高階微分、 $C^k$ 級について解説して、実際に偏微分可能かどうかを実例をもとに計算してみました。

偏微分は結局の所、形式的にはある変数に注目したとき、それ以外を定数と見て微分するということで、これはその変数方向の変化量を表しています。

次回は、偏微分の交換可能性について解説します。

乞うご期待！質問、コメントなどお待ちしております！

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

本記事の内容

多変数関数の微分のちょっとしたイントロ①

多変数関数の微分のちょっとしたイントロ②(微分から偏微分へ)

１変数の微分法のチャラい復習

偏微分のイントロ+全微分との関係

直感的な偏微分のイメージ

で、偏微分って何スか？

偏微分

で、結局偏微分って何なんですか？

偏導関数、高階微分、CkC^k級

いっちょ偏微分可能であることを証明してみっか。

結

コメントをする

偏導関数、高階微分、 $C^k$ 級