デデキントの切断？デデキントの定理の証明

本記事の内容
デデキントの切断について
言いたかったこと(デデキントの定理)
結

本記事の内容

本記事は

デデキントの切断
デデキントの定理

を説明し、デデキントの定理を証明する記事です。

本記事を読むにあたり、実数の連続性のイメージについて知っているとより理解が深まると思われますので、是非以下の記事も参照してください。

また、

この記事を理解するためには、集合および論理の初歩を理解していることが前提であるため、以下の記事も合わせて御覧ください。
※【論理と集合シリーズ】と銘打ってシリーズ化しているため、その一部のリンクを貼っています。

↓論理の初歩

↓集合の初歩

デデキントの切断について

デデキントの切断は「実数の数直線には”すき間”が無い」に対応します。
ここでは、「整数と有理数は知ってるが、実数なんて知らんヨ」という立場で書きます。

リヒャルト・デデキントは「連続性が担保される数があれば、その数は数直線を切断した面として捉えられるんじゃないか？」と思ったわけです。

整数の切断(直感的な理解)

まずは切断の直感的な理解を整数で説明します。
下図のように、整数の数直線を考えます。
このとき、$1$と$2$の間などには整数は存在していません($\displaystyle\frac{1}{2}$は整数でない)ので、”すき間”があります。

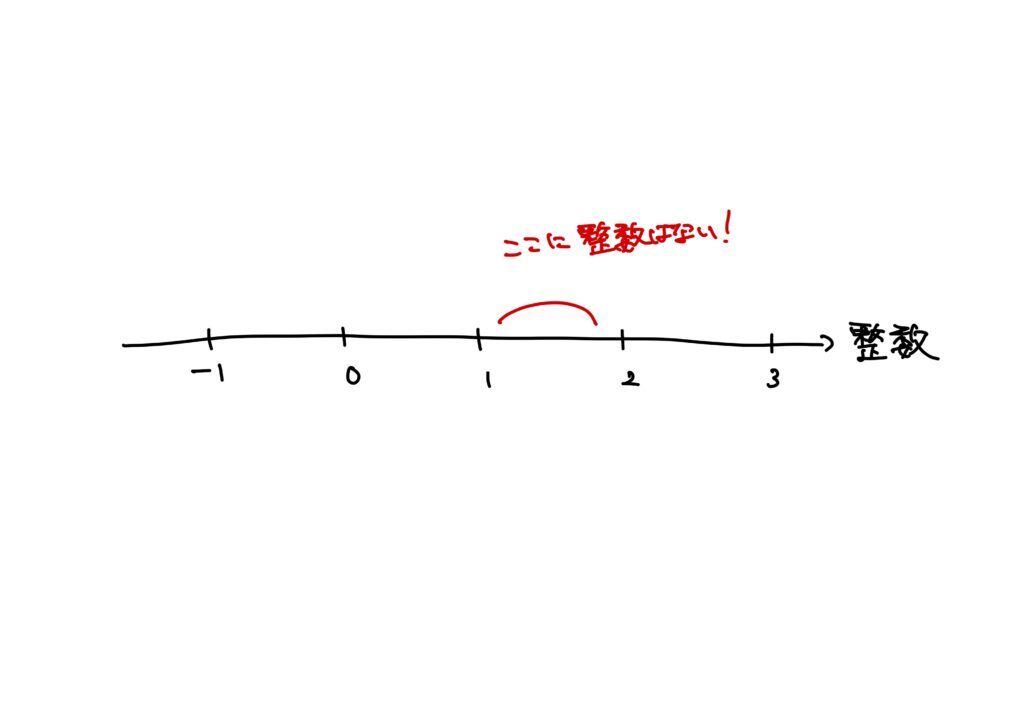
このとき、下図のように、この数直線を好きなところで切ります。
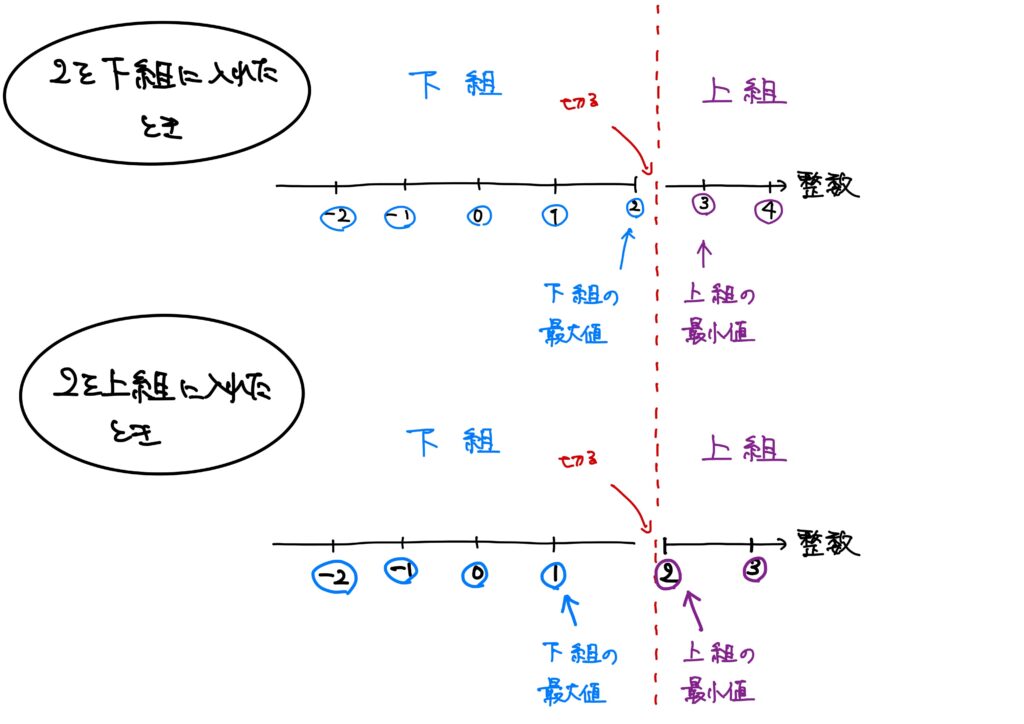
その切り口から左側を下組、右側を上組と呼ぶことにすると、下組には必ず最大値が存在して、上組には必ず最小値が存在します。

これは図のように、切り口が”すき間”にある場合だけに言えることではなく、切り口が数のところでも同じで、下組には最大値が、上組には最小値が存在します。
というのも、例えば$2$のところが切り口だったとして、この$2$を下組(上組でも良い)に入れたとき、下組の最大値は$2$で、上組の最小値は$3$です。
$2$を上組に入れたとき、下組の最大値は$1$で、上組の最小値は$2$です。

有理数の切断

今度は有理数について同じようにやってみましょう。
しかしながら、有理数の切断は整数ほど直感的には理解するのが難しいです。
というのも、有理数の数直線には一見すると”すき間”が無いように見えるからです。
例えば、こんな状況です。

オノコウスケ

$0$と$2$の間にある有理数ってどんなのがある？

たか

そりゃいっぱいありそうなもんだけれど、まず$1$があるよね。

オノコウスケ

そうだね。じゃあ$0$と$1$の間にある有理数ってどんなのがある？

たか

$\displaystyle \frac{1}{2}$とかじゃない？

オノコウスケ

そうだね。じゃあ$0$と$\displaystyle \frac{1}{2}$の間は？

たか

$\displaystyle \frac{1}{4}$とか。

というように、この操作はいくらでもできます($0$ともう一方の数を足して$2$で割ればいいから)。
すなわち、どんな$2$つの有理数の間にもまた有理数がある、という性質がある。
これを稠密性(ちゅうみつせい)という。
論理式で書けば、次です。

有理数の稠密性 $$(\forall a,b\in\mathbb{Q})a<b\Rightarrow\exists c\in\mathbb{Q}\ {\rm s.t.}\ a<c<b$$

稠密性というのは、直感的には「ぎっしり詰まっている」ということで、「であれば、有理数の数直線には”すき間”が無いのではないかネ？」となるかもしれません。
実は、有理数の数直線にはしっかり”すき間”があります。
これは後述する有理数の切断で説明します。

切断の数学的な理解

まずは「切断」というものを数学的に説明します。
言ってしまえば、「ある(大小関係があるような)集合に対する切断とはある特別な性質を持つ集合の組」のことです。
その性質というのは、

$2$つの集合の和集合は全体の集合と一致している。
$2$つの集合は接していない。（全体の集合はピッタリ$2$つに分かれている。）
$2$つの集合はそれぞれ空集合でない。（なにかしらの要素がある。）
片方の集合に入っている全ての要素は、もう一方の集合に入っている全ての要素よりも小さい。

ということです。
これを論理式で書くと、次です。

切断大小関係があるような集合$K$に対して、次を満たすような集合$A,B$の組$(A,B)$を$K$の切断という。

$K=A\cup B$
$A\cap B=\emptyset$,
$A\neq \emptyset$, $B\neq \emptyset$,
$a\in A$かつ$b\in B$ならば$a<b$.

先の整数の数直線を切る、ということを上記の切断に当てはめてみましょう。

例1.(切り口が”すき間”にあるとき)

$K=\mathbb{Z}$,
$A=\{x\in\mathbb{Z}\mid x\leq 1\}$,
$B=\{x\in\mathbb{Z}\mid x\geq 2\}$ .

とします。

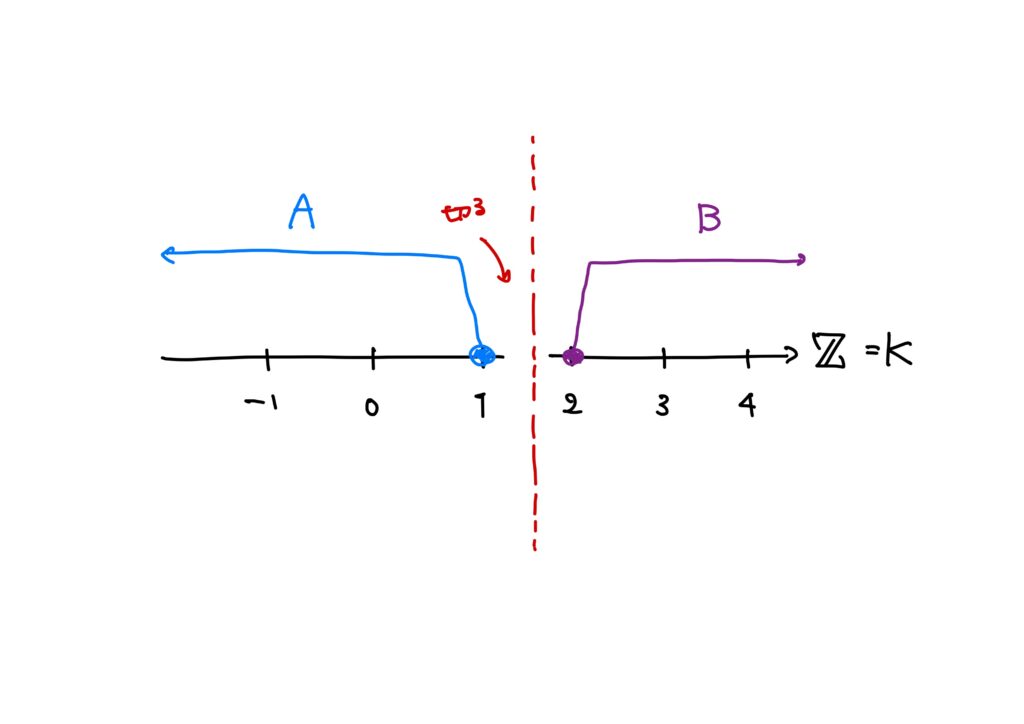
このとき、

$K=A\cup B$
「任意の$k\in K$に対して、$k\in A$または$k\in B$」、および「任意の$x$に対して、$x\in A\cup B$ならば$x\in K$」を示せば良いです。
（集合が等しいとはこれを示すことだった！）
任意の$k\in K$に対して、$K=\mathbb{Z}$であるため、$k\leq 1$か、$k\geq 2$のいずれか一方が成り立ちます。
実際、仮に$k\leq 1$かつ$k\geq 2$が成り立ったとすると(背理法！)、$2\leq k\leq 1$となり、$2\leq 1$を得ますが、これは矛盾です。
従って$k\in A$または$k\in B$ですから、$k\in A\cup B$です。
一方、任意の$x\in A\cup B$に対して、$x\in A$または$x\in B$ですが、$x\in A$であったとしても、$x\in B$であったとしても、$x\in\mathbb{Z}$であるため、$K=\mathbb{Z}$なのだから$x\in K$です。
$A\cap B=\emptyset$
仮に$A\cap B\neq\emptyset$だったとすると(背理法！)、ある$z$が存在して$z\in A\cap B$を満たします。
このときは、すでに1.で矛盾が生じることに言及しています。
$A\neq \emptyset$, $B\neq \emptyset$
$1\in A$かつ$2\in B$であるため、成り立ちます。
$a\in A$かつ$b\in B$ならば$a<b$.<br>
任意の$a\in A$に対して、$a\leq1$であり、任意の$b\in B$に対して、$2\leq b$であるから、$a\leq 1<2\leq b$により$a<b$です。

例2.(切り口に数があるとき)

$K=\mathbb{Z}$,
$A=\{x\in\mathbb{Z}\mid x\leq 1\}$,
$B=\{x\in\mathbb{Z}\mid x> 1\}$ .

とします。

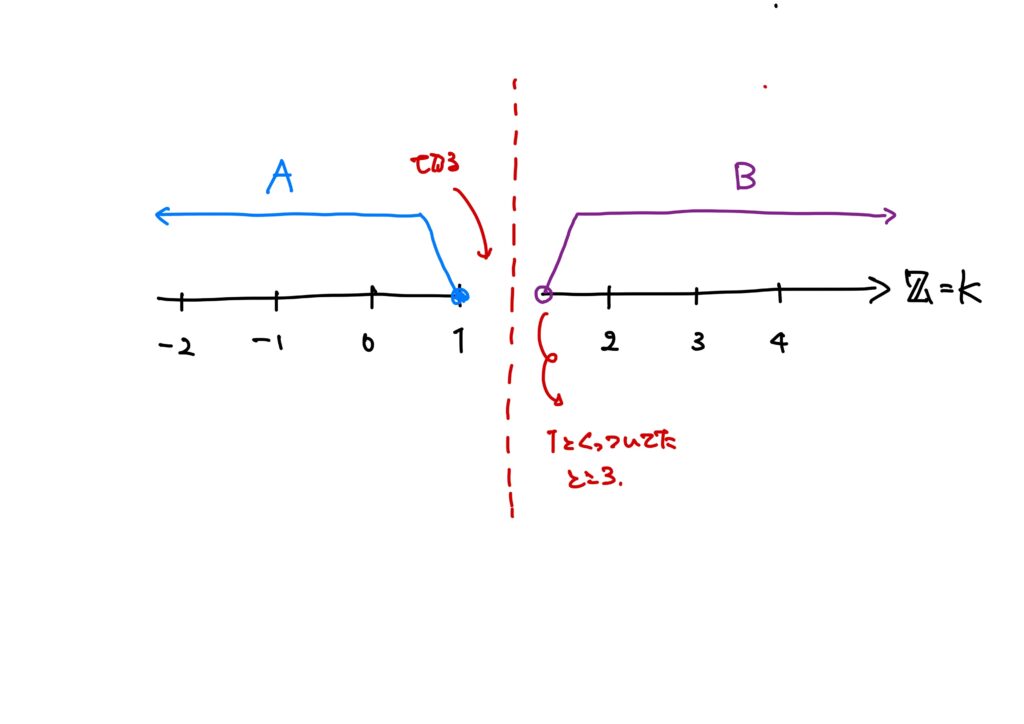
このとき、

$K=A\cup B$
「任意の$k\in K$に対して、$k\in A\lor k\in B$」および「任意の$x\in A\cup B$ならば$x\in K$」を示せば良いです。
任意の$k\in K$に対して、$K=\mathbb{Z}$であるため、$k\leq 1$か、$k> 1$のいずれか一方が成り立ちます。
実際、仮に$k\leq 1$かつ$k>1$が成り立ったとすると(背理法！)、「$(x<1$かつ$ x>1)$または$(x=1$かつ$x>1)$」が真です。
しかし、$1<x<1$なる整数$x$は存在しないため、「$x<1$かつ$x>1$」という命題は偽です。
さらに、「$x=1$かつ$x>1$」という命題も$1<1$となり、偽です。
これは矛盾です。
従って$k\in A$または$k\in B$です。
故に$k\in A\cup B$です。
一方、任意の$x\in A\cup B$に対して、$x\in A$または$x\in B$ですが、$x\in A$であったとしても、$x\in B$であったとしても、$x\in\mathbb{Z}$であるため、$K=\mathbb{Z}$なのだから$x\in K$です。
$A\cap B=\emptyset$
仮に$A\cap B\neq\emptyset$だったとすると(背理法！)、ある$z$が存在して$z\in A\cap B$を満たします。
このときは、すでに1.で矛盾が生じることに言及しています。
$A\neq \emptyset$, $B\neq \emptyset$
$1\in A$かつ$2\in B$であるため、成り立ちます。
$a\in A$かつ$b\in B$ならば$a<b$
任意の$a\in A$に対して、$a\leq1$であり、任意の$b\in B$に対して、$2< b$であるから、$a\leq 1<b$により$a<b$です。

有理数の切断

整数の切断のときと同じようなことをしてみましょう。

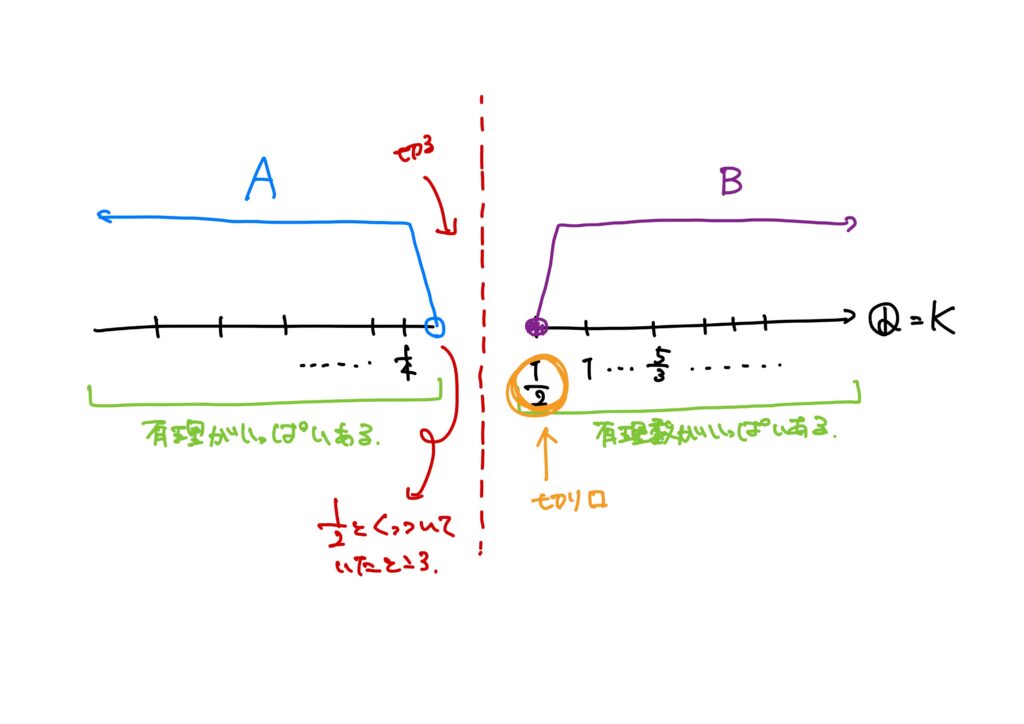
例3.

$K=\mathbb{Q}$,
$A=\{q\in\mathbb{Q}\mid q<\displaystyle \frac{1}{2}\}$,
$B=\{q\in\mathbb{Q}\mid q\geq\displaystyle \frac{1}{2}\}$,

とすると、$(A,B)$は切断です。

このとき、

$K=A\cup B$
「任意の$k\in K$に対して、$k\in A\lor k\in B$」および「任意の$x$に対して、$x\in A\cup B$ならば$x\in K$」を示せば良いです。
任意の$k\in K$に対して、$K=\mathbb{Q}$であるため、$k<\displaystyle\frac{1}{2}$か、$k\geq\displaystyle\frac{1}{2}$のいずれか一方が成り立ちます。
実際、仮に$k<\displaystyle\frac{1}{2}$かつ$k\geq\displaystyle\frac{1}{2}$が成り立ったとすると(背理法！)、「$(x<\displaystyle \frac{1}{2}$かつ$x>\displaystyle\frac{1}{2})$または$(x=\displaystyle\frac{1}{2}$かつ$x>\displaystyle\frac{1}{2})$」が真です。
しかし、$\displaystyle\frac{1}{2}<x<\displaystyle\frac{1}{2}$なる有理数$x$は存在しないため、「$x<\displaystyle\frac{1}{2}$かつ$x>\displaystyle\frac{1}{2}$」という命題は偽です。
さらに、「$x=\displaystyle\frac{1}{2}$かつ$x>\displaystyle\frac{1}{2}$」という命題も$\displaystyle\frac{1}{2}<\displaystyle\frac{1}{2}$となり、偽です。
これは矛盾です。
従って$k\in A$または$k\in B$であるから、$k\in A\cup B$です。
一方、任意の$x\in A\cup B$に対して、$x\in A$または$x\in B$ですが、$x\in A$であったとしても、$x\in B$であったとしても、また$x\in A\cap B$だったとしても、$x\in\mathbb{Q}$であるため、$K=\mathbb{Q}$ですから$x\in K$です。
$A\cap B=\emptyset$
仮に$A\cap B\neq\emptyset$だったとすると(背理法！)、ある$z$が存在して$z\in A\cap B$となります。
このときは、すでに1.で矛盾が生じることに言及しています。
$A\neq \emptyset$, $B\neq \emptyset$
$\displaystyle\frac{1}{4}\in A$かつ$\displaystyle\frac{3}{2}\in B$であるため、成り立ちます。
$a\in A\land b\in B\Rightarrow a<b$
任意の$a\in A$に対して、$a<\displaystyle\frac{1}{2}$であり、任意の$b\in B$に対して、$\displaystyle\frac{1}{2}\leq b$であるから、$a\leq \displaystyle\frac{1}{2}<b$により$a<b$です。

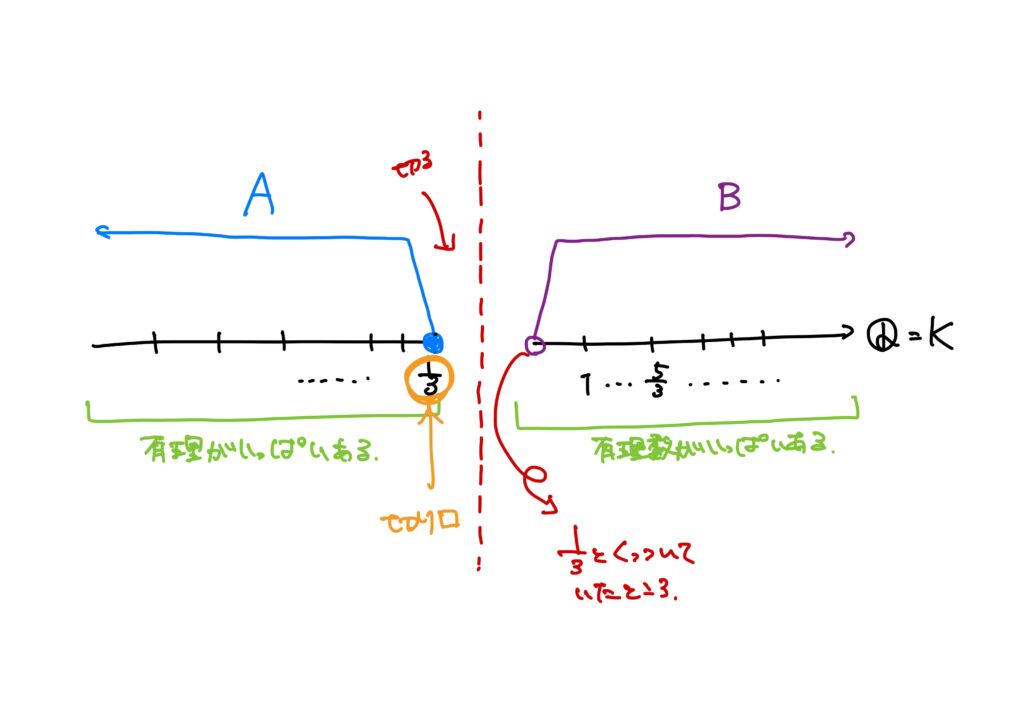
例4.

$K=\mathbb{Q}$,
$A=\{q\in\mathbb{Q}\mid q\leq\displaystyle \frac{1}{3}\}$,
$B=\{q\in\mathbb{Q}\mid q>\displaystyle \frac{1}{3}\}$,

とすると、$(A,B)$は切断です。

このとき、

$K=A\cup B$
$A\cap B=\emptyset$
$A\neq \emptyset$, $B\neq \emptyset$
$a\in A$かつ$b\in B$ならば$a<b$

が成り立ちます。
ただし、証明は例3.と殆ど同じですので、省略します。

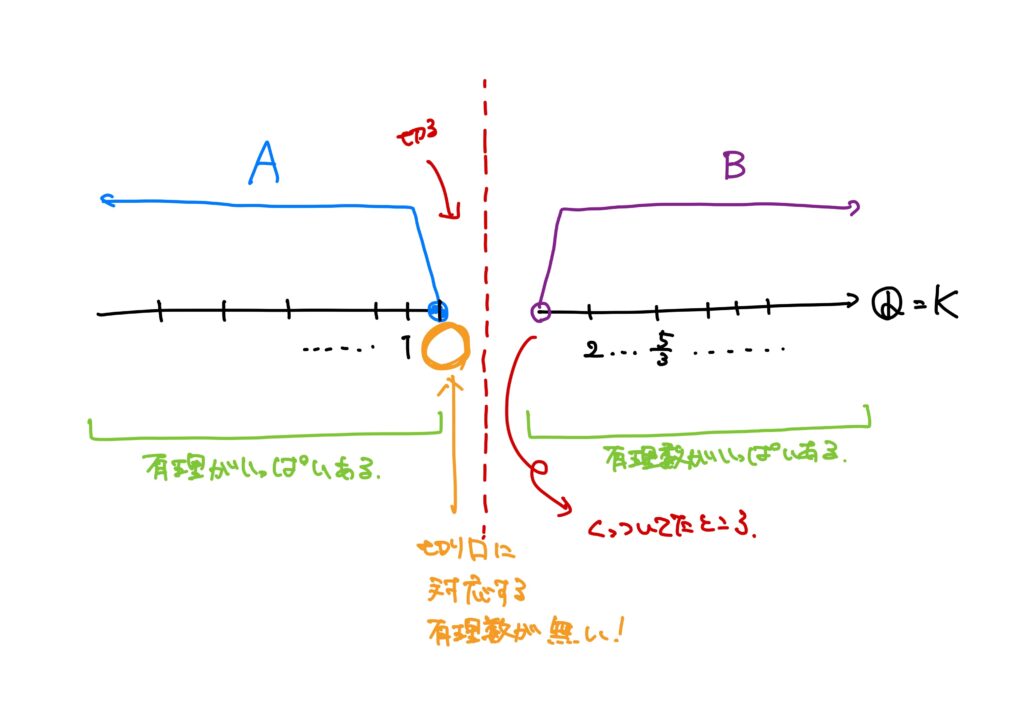
例5.（重要）
負の有理数の集合を$\mathbb{Q}^-=\{q\in\mathbb{q}\mid q<0\}$と書くことにします。
このとき、

$K=\mathbb{Q}$,
$A=\{q\in\mathbb{Q}\mid q^2\leq2\}\cup\mathbb{Q}^-$,
$B=\{q\in\mathbb{Q}\mid q^2>2\}$,

とすると、$(A,B)$は切断です。

$K=A\cup B$
「任意の$k\in K$に対して、$k\in A$または$k\in B$」および「任意の$x$に対して$x\in A\cup B$ならば$x\in K$を示せば良いです。
任意の$k\in\mathbb{Q}$に対して、$k=0$,$k>0$,$k<0$のいずれかが成り立ちます。
$k=0$のとき、$k\in A$です。
$k<0$のときは$k\in\mathbb{Q}^-\subset A$ですので、$k\in A$です。
$k>0$のとき、$k^2>2$か$k^2\leq 2$のいずれかが成り立つことを示せば良いです。
仮に$k^2>2$かつ$k^2\leq 2$であれば、$2<k^2\leq 2$となり、$2<2$となるから矛盾です。
従って、$k^2>2$と$k^2\leq 2$のいずれか一方が成り立ちます。
故に$k\in A\cup B$が成り立ちます。
一方、任意の$x\in A\cup B$に対して、$x\in A$または$x\in B$ですが、$x\in A$であったとしても、$x\in B$であったとしても、また$x\in A\cap B$だったとしても、$x\in\mathbb{Q}$であるため、$K=\mathbb{Q}$ですから$x\in K$です。
$A\cap B=\emptyset$
仮に$A\cap B\neq\emptyset$だったとすると(背理法！)、ある$z$が存在して$z\in A\cap B$を満たします。
このときは、すでに1.で矛盾が生じることに言及しています。
$A\neq \emptyset$, $B\neq \emptyset$
$\displaystyle-\frac{1}{4}\in A$かつ$\displaystyle\frac{3}{2}\in B$ですので、成り立ちます。
$a\in A$かつ$b\in B$ならば$a<b$
任意の$a\in A$に対して、「$(a<0)$または$(a>0$かつ$a^2\leq 2)$」です。
また、任意の$b\in B$に対して、「$(b>0)$かつ$(a>0$かつ$b^2>2)$」です。
従って、$a^2\leq 2<b^2$です。
$a<0$ならば、$b>0$により$a<b$です。
$a>0$かつ$a^2<2$であれば、$a^2<b^2$と$(a+b)(a-b)<0$は同値ですので$-b<a<b$だから$a<b$である。

例3,4,5を見てみると、それぞれ

例3:下組に最大値が無い、かつ上組に最小値がある。(切り口に対応する数有)
例4:下組に最大値があり、かつ上組に最小値がない。(切り口に対応する数有)
例5:下組に最大値が無く、かつ上組にも最小値がない。($q^2=2$という有理数は存在しないから。)(切り口に対応する数無)

という場合です。
※例5.の場合は$(0,1]$に最大値$1$はあるけど、最小値は存在しない、と高校で習ったと思います。

	最大値	最小値	切り口に対応する数
例3	なし	$\frac{1}{2}$	$\frac{1}{2}$
例4	$\frac{1}{3}$	なし	$\frac{1}{3}$
例5	なし	なし	なし

このとき、重要なのは

例3および例4の場合は切断したときの切り口に対応する数(それぞれ$\displaystyle\frac{1}{2}$、$\displaystyle\frac{1}{3}$)があるけれど、例5の場合には切り口に対応する数が存在しない！

ということです。
これはすなわち、

有理数の数直線には”すき間”がある！

ということです。
ちなみに、場合としては

下組に最大値があり、かつ上組に最小値ある

も考えうるのですが、この場合は有理数では起こり得ません。
仮に$A,B$が有理数の部分集合で、$A$には最大値$a$が、$B$には最小値$b$があったとします。
このとき、有理数の稠密性から、$a$と$b$の間には必ず有理数$c$が存在します($a<c<b$を満たす有理数$c$が存在する)。
しかしこの$c$は有理数であるにも関わらず、$A$の要素でもなければ、$B$の要素でもありません。
したがって、切断の条件$\mathbb{Q}=A\cup B$を満たしません。
故に、この場合は起こり得ないのです。

さて、例5には切り口に対応する数が存在しない、と述べたのですが、素朴に「であれば、その切り口にある数はどんな数かネ？」という疑問が生まれます。
この数こそが無理数なのです
例5.の場合、すなわち有理数の切断において、下組に最大値が無く、上組にも最小値がないような切断に対して、その切り口である$q^2=2$(あくまで一例)を満たす数を無理数と呼ぶというわけです。

ここで「$q^2=2$なんていう数はあるんすか？」というツッコミが論破王から来そうなので、解説しておきます。
答えは「あります」です。
それは、$1$辺が$1$kmの正方形の土地を考えます。
この土地の対角線の長さは三平方の定理から$q^2=2$kmを満たす数です。
つまり、$q^2=2$kmを満たす数$q$を作図することができます。
すなわち、$q^2=2$を満たす数は実在するのです。

以上により、有理数と無理数をあわせた集合において切断を考えると、必ず切り口に対応する数が存在することになります。
したがって、有理数と無理数を合わせた集合には一切”すき間”が無いということなのです。
有理数と無理数をあわせた集合の要素を実数と呼ぶことで、実数には一切すき間がない、と言えるのである。

「実数って？」という疑問に対する回答

先に「実数は有理数と無理数をあわせた集合の要素だ」と述べました。
これは、有理数と無理数をあわせた集合に切断を考えることに寄って、一切”すき間”が無いということから言えます。
つまり、有理数の切断の切り口には必ず数が対応してますよ、と言っているわけす。
従って、「有理数の切断の切り口を実数と呼ぶんですよ」と言っても良いのです。
更に言い換えれば、「有理数の切断の切り口には必ず数が対応するのだから、切断を考える、ということは$1$つの有理数を考えることと同じことだよね」ということもできます。
すなわち、

実数有理数の集合$\mathbb{Q}$のデデキント切断$(A,B)$を実数と呼ぶ。実数を全て集めてきた集合を$\mathbb{R}$(Real numberのR）と書く。

言いたかったこと(デデキントの定理)

本記事で言いたかったことは、実数の集合に対して次の定理が成り立つということです。

デデキントの定理 実数の集合$\mathbb{R}$の任意の切断$(A,B)$に対して、ある実数$r$が存在して、次の2つのいずれか一方が成り立つ。

$A$には最大値が無く、$B$には最小値$r$がある。
$A$には最大値$r$があり、$B$には最小値がない。

つまり、切断で考えられる4パターンのうち、実数の切断では下組と上組のどちらか一方に最大値または最小値があるパターンに限る、ということです。
さらにいえば、実数の切断では、切り口に必ず数が存在してますよ、ということである。

結

今回は「デデキントの切断」と「デデキントの定理」を説明して、証明を与えました。
デデキントの定理は

実数の数直線上には一切”すき間”が無い。

という直感に対応する概念です。

次回は、「上に有界、上界、上限、下に有界、下界、下限」を説明します。

乞うご期待！質問、コメントなどお待ちしております！

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34