本記事の内容
本記事は平均値の定理のイメージとその証明を与える記事です。
「証明だけ知りたいのだがネ?」という方は平均値の定理の証明まで飛んでください。
本記事を読むにあたり、ロルの定理について知っている必要があるため、以下の記事も合わせてご覧ください。
平均値の定理のイメージ
平均値の定理のイメージはなんてことありません。
「当然じゃね?」なる方も多いと思います(かくいう筆者もそう思っています)。
平均値の定理を平たく言えば、
ということです。
「文章じゃわかりにくいわ!」となるかもしれませんので、図で説明します。
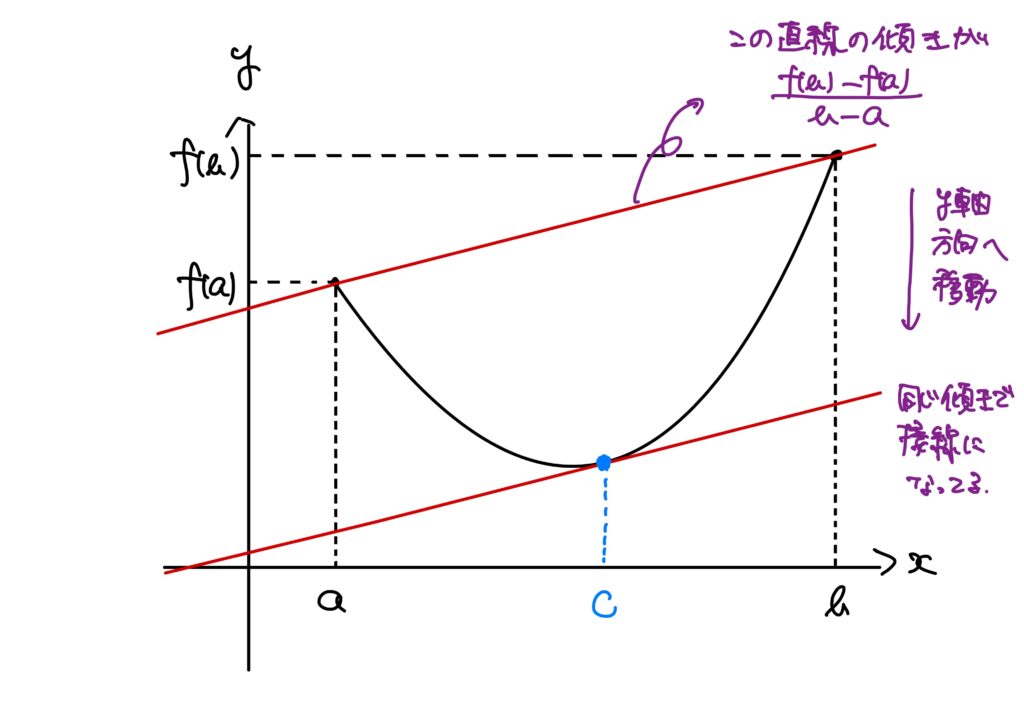
このように、閉区間での関数の値同士を結んでできる直線を描いたとき、その直線と同じ傾きの接線が描けまっせ、ということです。
少々数学的に言えば、
ということになります。
つまり、\(f(b)\)と\(f(a)\)を結んでできる直線を上下に(\(y\)軸方向に)平行移動すれば、必ず\(f\)の接線になりますよ、ということです。
もちろんこの\(c\in(a,b)\)は1つとは限りません。
以下のような場合もあります。
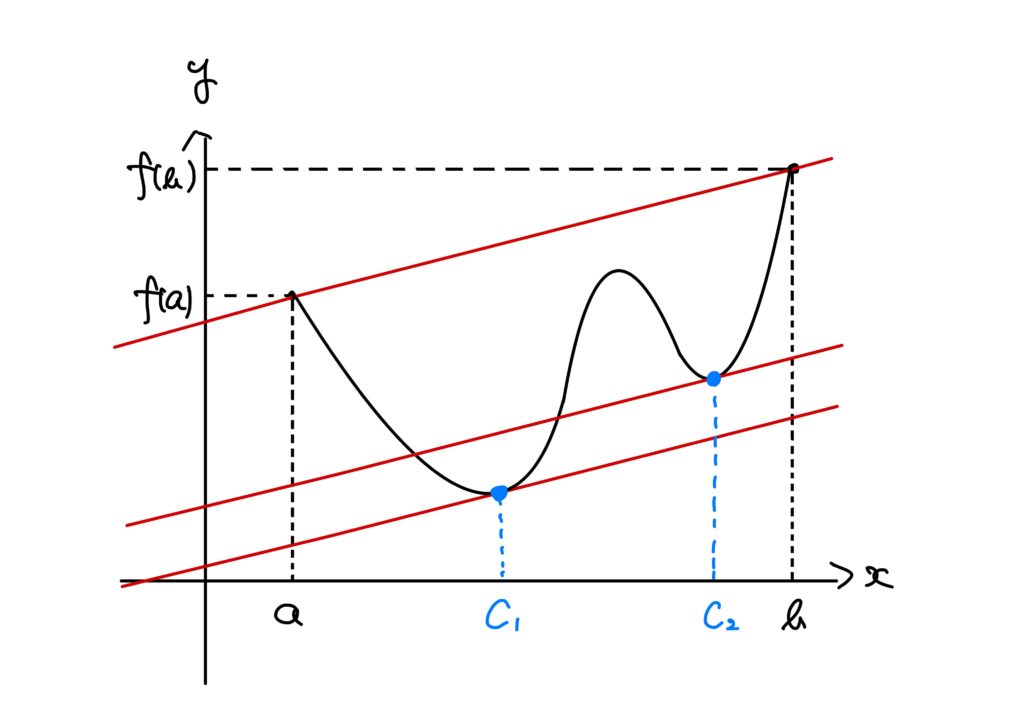
では、平均値の定理を明示して証明しましょう!
平均値の定理の明示とその証明
平均値の定理の明示
平均値の定理を数学的に明示すると、次です。

これを証明します。
と、その前に証明の発想を説明します。
平均値の定理の証明の発想
平均値の定理を少々観察してみましょう。
筆者が大学1年生のとき、教授が「グッと睨むとこうなりますよね?」という表現をして行間を飛ばされ混乱した記憶があります(笑)
そんな話は置いておいて、グッと睨んでみましょう。(行間は飛ばしませんのでご安心を)
平均値の定理において、仮に\(f(b)\)と\(f(a)\)が等しかったら、すなわち\(f(b)=f(a)\)であれば、\(f(b)-f(a)=0\)ですので、\(\displaystyle\frac{f(b)-f(a)}{b-a}=0\)です。
すると、前回(【解析学の基礎シリーズ】1変数実数値関数の微分編 その7)証明した「ロルの定理と似てないか?」となります。
ロルの定理は何だったか、というと、
(平均値の定理の証明へジャンプ)
でした。
ロルの定理の証明は【解析学の基礎シリーズ】1変数実数値関数の微分編 その7を御覧ください。
これを見ると、「似てるどころか同じではないかネ?」となると思います。
そうです。同じです。
つまり、平均値の定理はロルの定理のある種の一般化となっています。
ロルの定理の\(f(b)\)と\(f(a)\)が一致していないくても、\(f(b)\)と\(f(a)\)を結んでできる直線と同じ傾きの接線が描けるということを主張しているのが平均値の定理なのです。
ロルの定理においては\(f(b)=f(a)\)ですので、傾きが\(0\)だった、とういうことなのです。
ここに気がつくことができれば、「ロルの定理を使えるのではないかネ?」という発想に至るわけです。
すなわち、「ロルの定理を使えるように\(f(x)\)を使った新しい関数\(g(x)\)を作ろうぜ」という話になるわけです。
\(g:[a,b]\to\mathbb{R}\)が満たしてほしい条件としては、
- \(g(a)=g(b)\)、
- \(g\)は\((a,b)\)で微分可能、
- \(g\)は\([a,b]\)で連続
です。
もしこれが成り立てば、ロルの定理から\(g^\prime(c_0)=0\)という\(c_0\in(a,b)\)を見つけることができます。
目標を思い出しておくと、\(\displaystyle\frac{f(b)-f(a)}{b-a}=f^\prime(c)\)という\(c\in(a,b)\)を見つけたいわけです。
式変形をして、\(\displaystyle f^\prime(c)-\frac{f(b)-f(a)}{b-a}=0\)という\(c\in(a,b)\)を見つけたいわけです。
今、\(g^\prime(c_0)=0\)ですので、\(\displaystyle f^\prime(c)-\frac{f(b)-f(a)}{b-a}=g^\prime(c_0)\)を満たすような\(c\)と\(g\)を見つけたいということに言い換えることができます。
もしそのような\(g\)が見つけられたらば、\(c_0\)を見つけることができるため、\(c\)の候補として\(c_0\)が挙げられます。
\(c\)として\(c_0\)を採用すると、\(\displaystyle f^\prime(c_0)-\frac{f(b)-f(a)}{b-a}=g^\prime(c_0)\)となります。
ここで、1次関数\(y=tx\ (t\neq0)\)を微分すると\(y^\prime=t\)ということを思い出せば、「\(\displaystyle f(x)-\frac{f(b)-f(a)}{b-a}x=g(x)\)とすればいいんじゃないか?」となるわけです。
このように\(g\)を決めたとすると、\(\displaystyle g(a)=f(a)-\frac{f(b)-f(a)}{b-a}a\)、\(\displaystyle g(b)=f(b)-\frac{f(b)-f(a)}{b-a}b\)となって必ずしも\(g(a)\)と\(g(b)\)は等しくありません。
従って、ちょっと改良してみます。
どうするかというと、\(\displaystyle f(x)-\frac{f(b)-f(a)}{b-a}x\)の\(x=a\)での値と\(x=b\)での値を一致させたいので、今回はこの値を\(f(a)\)と一致させるように改良してみます(もちろん\(f(b)\)でもOKです)。
さて、\(x=a\)でのこの関数の値は\(\displaystyle f(a)-\frac{f(b)-f(a)}{b-a}a\)でした。
これを改良してどうにか\(f(a)\)と一致させたいわけです。
すると、\(\displaystyle-\frac{f(b)-f(a)}{b-a}a\)の部分が邪魔なので、これが\(0\)だったら嬉しいです。
故に、\(x=a\)を代入したときに、\(\displaystyle-\frac{f(b)-f(a)}{b-a}a\)の部分が\(0\)になってほしいので、\(\displaystyle-\frac{f(b)-f(a)}{b-a}x\)の部分を\(\displaystyle-\frac{f(b)-f(a)}{b-a}(x-a)\)としてみます。
すなわち、新たに
$$g(x)=f(x)-\frac{f(b)-f(a)}{b-a}(x-a)$$
としてみます。
すると、
- \(\displaystyle g(a)=f(a)\)、
- \(\displaystyle g(b)=f(b)-\frac{f(b)-f(a)}{b-a}(b-a)=f(b)-f(b)+f(a)=f(a)\)
となって、\(g(a)=g(b)\)です。
「よっしゃ!」といった感じです。
しかし、まだ考えなければならないことがあります。
それは\(g\)の連続性と微分可能性です。
とはいえ、これはすでに担保されているようなものです。
というのも、そもそも仮定から\(f\)は\([a,b]\)で連続で\((a,b)\)で微分可能です。
また、\(\displaystyle\frac{f(b)-f(a)}{b-a}(x-a)\)は一次関数ですので、\(\mathbb{R}\)で連続かつ微分可能です。
※多項式関数(1次関数の一般化)の連続性については【解析学の基礎シリーズ】関数の極限編 その8を、微分可能性については【解析学の基礎シリーズ】1変数実数値関数の微分編 その5を御覧ください。
さてさて、この発想に至ったらば、後はそれは体裁を整えつつ文章に直せば証明となります。
平均値の定理の証明
発想の部分が少々長くなってしまったので、平均値の定理を再掲します。
では行きましょう!
証明
示したいことは
$$
(\exists c\in(a,b))\ {\rm s.t.}\ \frac{f(b)-f(a)}{b-a}=f^\prime(c)
$$
です。
すなわち、上記を満たす\(c\in(a,b)\)を見つけることで証明完了です。
\(x\in[a,b]\)に対して、
$$g(x)=f(x)-\frac{f(b)-f(a)}{b-a}(x-a)$$
とすると、\(f\)は\([a,b]\)で連続であり、\(\displaystyle-\frac{f(b)-f(a)}{b-a}(x-a)\)は1次関数ですので、\(\mathbb{R}\)で連続だから、\(g\)は\([a,b]\)で連続です。
また、\(f\)は\((a,b)\)で微分可能であり、\(\displaystyle-\frac{f(b)-f(a)}{b-a}(x-a)\)は1次関数ですので、\(\mathbb{R}\)で微分可能だから、\(g\)は\((a,b)\)で微分可能です。
さらに、
- \(\displaystyle g(a)=f(a)-\frac{f(b)-f(a)}{b-a}(a-a)=f(a)-0=f(a)\)、
- \(\displaystyle g(b)=f(b)-\frac{f(b)-f(a)}{b-a}(b-a)=f(b)-f(b)+f(a)=f(a)\)
ですので、\(g(a)=g(b)\)です。
従って、\(g\)はロルの定理の仮定を満たします。
故に、
$$
(\exists c_0\in(a,b))\ {\rm s.t.}\ g^\prime(c_0)=0
$$
が成り立ちます。
つまり、上記を満たすような\(c_0\in(a,b)\)を見つけてくることができます。
ここで、
$$
g^\prime(c_0)=f^\prime(c_0)-\frac{f(b)-f(a)}{b-a}
$$
ですので、\(g^\prime(c_0)=0\)だから、
$$
f^\prime(c_0)-\frac{f(b)-f(a)}{b-a}=0
$$
です。
従って、
$$f^\prime(c_0)=\frac{f(b)-f(a)}{b-a}$$
となるため、\(c\)として\(c_0\)を採用すれば良い事がわかります。
証明終わり
結
今回は平均値の定理のイメージとその証明を行いました。
平均値の定理を平たく言えば、
ということでした。
また、平均値の定理はロルの定理から導かれる事実であるのと同時に、ロルの定理の一般化(より広い範囲での主張)です。
次回は高校数学でも出現した「微分係数が正(負)ならば狭義単調増加(減少)関数」、「微分係数\(=0\)であれば定数関数」ということを示します。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする