本記事の内容
本記事はワイエルシュトラスの最大値定理(最大値の定理、最大値最小値定理)のイメージを説明する記事です。
本記事を読むにあたり、関数の連続とはどういうことかを知っているとよりイメージが湧きやすいと思われますので、その際は以下の記事を参照してください。
また、中間値の定理のイメージも知っているとより良いと思われますので、合わせてご覧ください。
関数の連続性のイメージの復習
関数の連続性のイメージは【解析学の基礎シリーズ】関数の極限編 その4で説明したとおり、
ということでした。
関数が(閉区間で)”つながっている”ことで得られる事実うちの1つが「ワイエルシュトラスの最大値定理」なのです。
※関数の連続性の数学的な説明は【解析学の基礎シリーズ】関数の極限編 その5を御覧ください。
では早速中間値の定理のイメージを説明します。
例と共に見るワイエルシュトラスの最大値定理のイメージ
ワイエルシュトラスの最大値定理はどういう主張なのか、ということを説明する前にまずどういう状況かを考え、どういうことが言えそうか(すなわち、どういう発想でワイエルシュトラスの最大値定理が成り立つと予想されたか)を説明します。
例
例1.\(\displaystyle f_1:\left[ -\frac{\pi}{2},\frac{5}{2}\pi \right]\to\mathbb{R}\)、\(f_1(x)=\sin x\)
以前の記事(【解析学の基礎シリーズ】関数の極限編 その12)で述べたとおり、この関数は\(\displaystyle \left[ -\frac{\pi}{2},\frac{5}{2}\pi \right]\)で連続です。
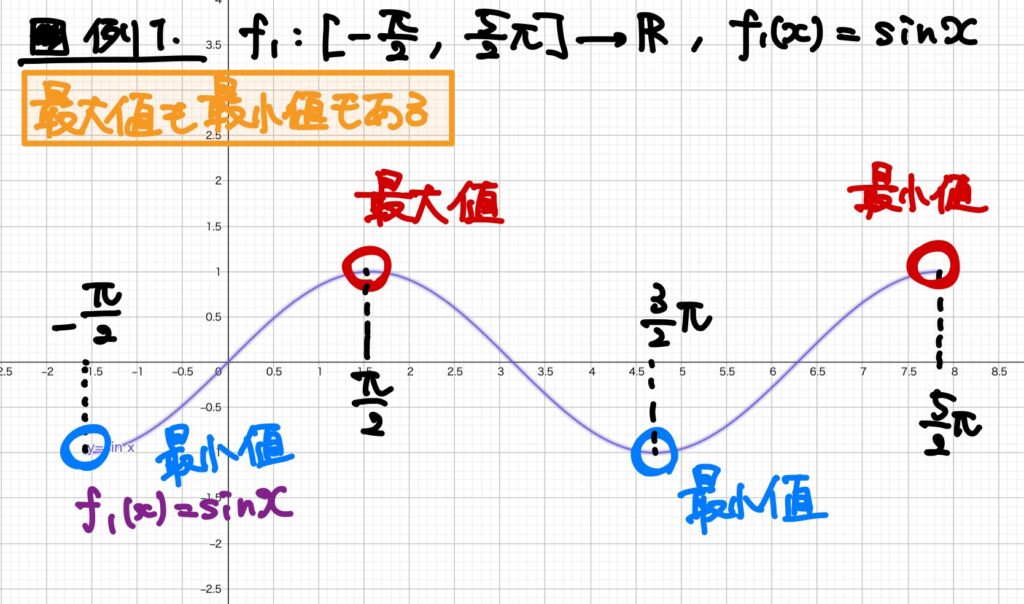
この図において、関数\(f_1\)は次のことが分かります。
- \(\displaystyle x=\frac{\pi}{2},\ \frac{\pi}{2}\)で最大値\(\displaystyle f_1\left( \frac{\pi}{2}\right)=f_1\left( \frac{5}{2}\pi \right)=1\)を取ります。
- \(\displaystyle x=-\frac{\pi}{2},\ \frac{3}{2}\pi\)で最小値\(\displaystyle f_1\left( -\frac{\pi}{2}\right)=f_1\left( \frac{3}{2}\pi \right)=-1\)を取ります。
例2.\(\displaystyle f_2:[ -2,0)\cup(0,2]\to\mathbb{R}\)、\(\displaystyle f_2(x)=\frac{1}{x^2}\)
\(f_2\)は\(x=0\)で不連続です。
この図において、関数\(f_2\)は次のことが分かります。
- 最大値は存在しません。
- \(x=-2,\ 2\)で最小値\(f_2(-2)=f_2(2)=1\)を取ります。
このように、閉区間で連続な関数に対しては必ず最大値も最小値も両方存在します。
これがワイエルシュトラスの最大値定理です。
とはいえ、少々注意が必要です。
というのも、「不連続であっても最大値と最小値の両方が存在する場合もある」からです。

例3.\(f_3:[0,5]\to\mathbb{R}\),
$$f_3(x)=\begin{cases}
x+2 & (1\leq x\leq 5)\\
x-3 & (0\leq x<1)
\end{cases}
$$
この関数は連続ではありません。

この関数は連続でないのにも関わらず、
- \(x=5\)で最大値\(f_3(5)=7\)を取ります。
- \(x=0\)で最小値\(f_3(0)=-3\)を取ります。
という事が分かります。
混乱してしまうかもしれませんが、何が言いたいかというと、
ということです。
ワイエルシュトラスの最大値定理のイメージ図
「つまり、ワイエルシュトラスの最大値定理ってどういうことなの?」ということを説明する図が以下です。
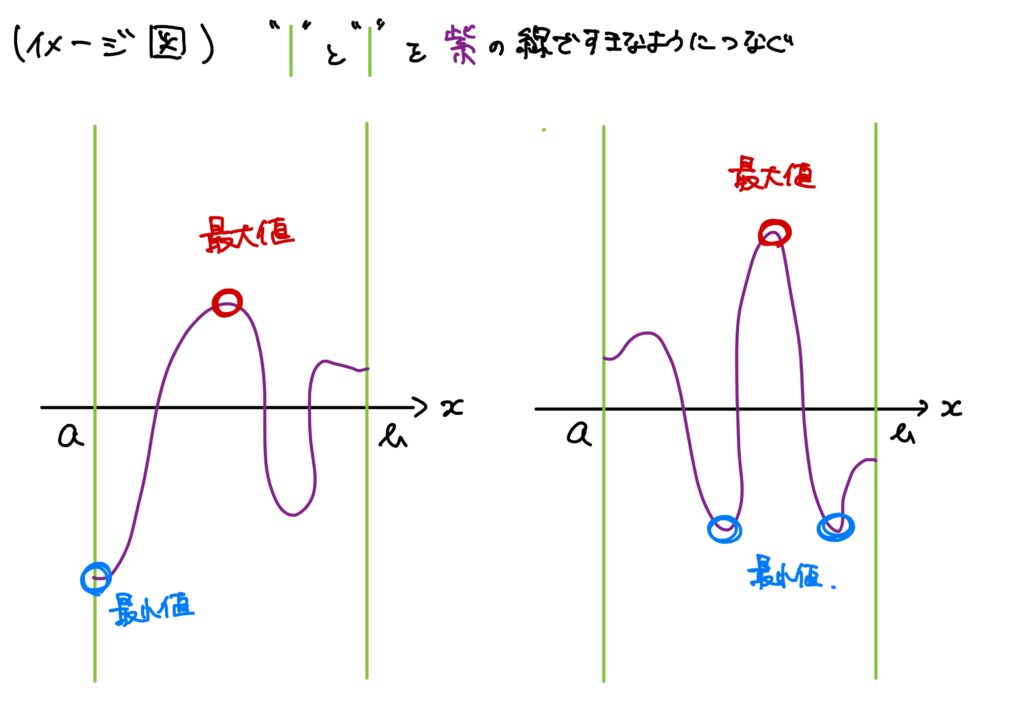
このように、途切れることなくつないだとき、つないだ線には必ず一番大きいところ(最大値)と一番小さいところ(最小値)の両方が存在します。
この「途切れることなくつないだとき」が関数の連続性に対応します。
(図を見ると「そりゃそうだな」と筆者は思いました。)
連続でない関数については、例2.で見たとおり、最大値と最小値が一方しか存在しない場合があります。
連続であるという条件は「閉区間で」という条件が付きます。
なぜかを以下で説明します。
ワイエルシュトラスの最大値定理のポイント
以上のことをまとめれば、ワイエルシュトラスの最大値定理のイメージは
ということです。
ここで、「開区間じゃだめなのけ?」と中間値の定理のときと同様に思うかもしれません。
実はダメなんです。
これは\(\tan x\)を考えてみると直ちに分かります。
例4. \(\displaystyle f_4:\left( -\frac{\pi}{2},\frac{\pi}{2} \right)\to\mathbb{R}\)、\(f_4(x)=\tan x\)とします。
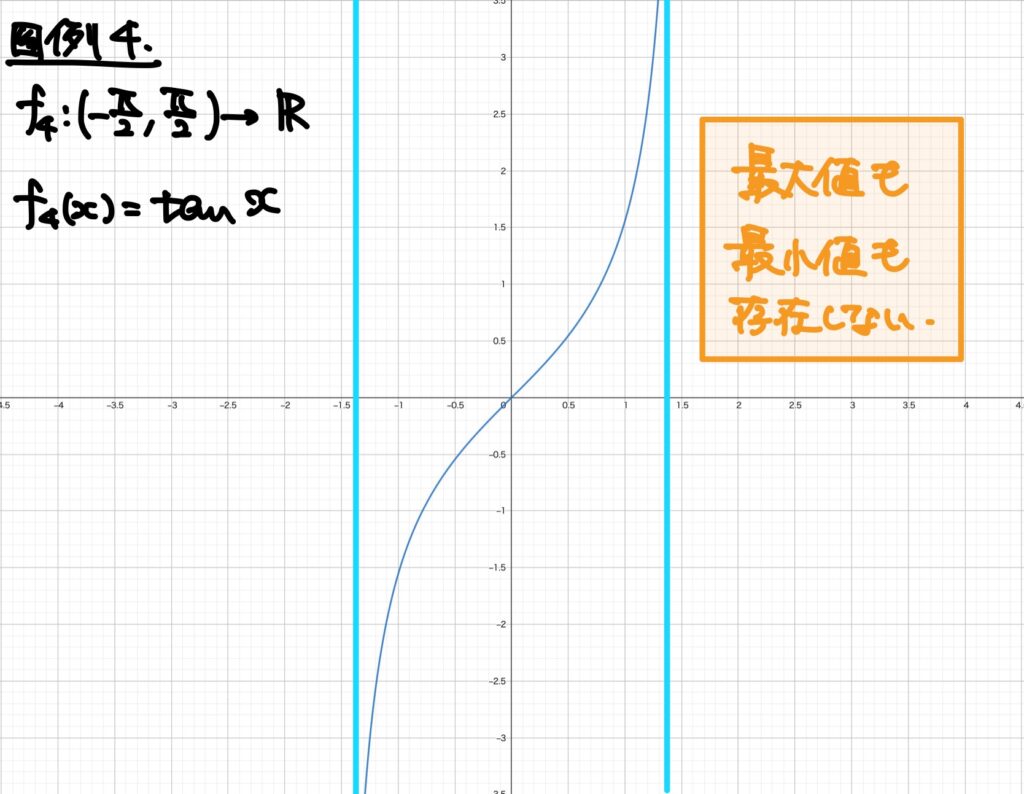
この関数は\(\displaystyle \left( -\frac{\pi}{2},\frac{\pi}{2} \right)\)で連続です。
しかしながら、最大値も最小値も存在しません。
このように開区間で連続だったとしても、最大値、最小値が存在しない場合があります。
故にワイエルシュトラスの最大値定理には「閉区間で連続」という条件が必要なのです。
結
今回はワイエルシュトラスの最大値定理のイメージを説明しました。
この定理のイメージとしては、
ということで、閉区間で連続じゃないとダメだよ、ということも注意しました。
主観ですが、筆者が最初のこの定理を見たときに「当たり前じゃね?」と思いました。
また同時に「こんな当たり前のことをどう証明するんだ?」とも思いました。
次回はワイエルシュトラスの最大値定理を数学的に明示して、さらに証明も与えます。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ1冊持っておくと良いと思います!





コメントをする