本記事の内容
本記事は関数の収束は数学的にどういうことかを説明し、実際に関数の収束を証明してみる記事である。
本記事を読むにあたり数列の収束を理解し、関数の収束のイメージがついているとより理解しやすいと思われるので、その際は以下の記事を参照してください。
関数の収束って?
関数の収束を論理式で書くと、次である。
直感的に言い直しておくと、
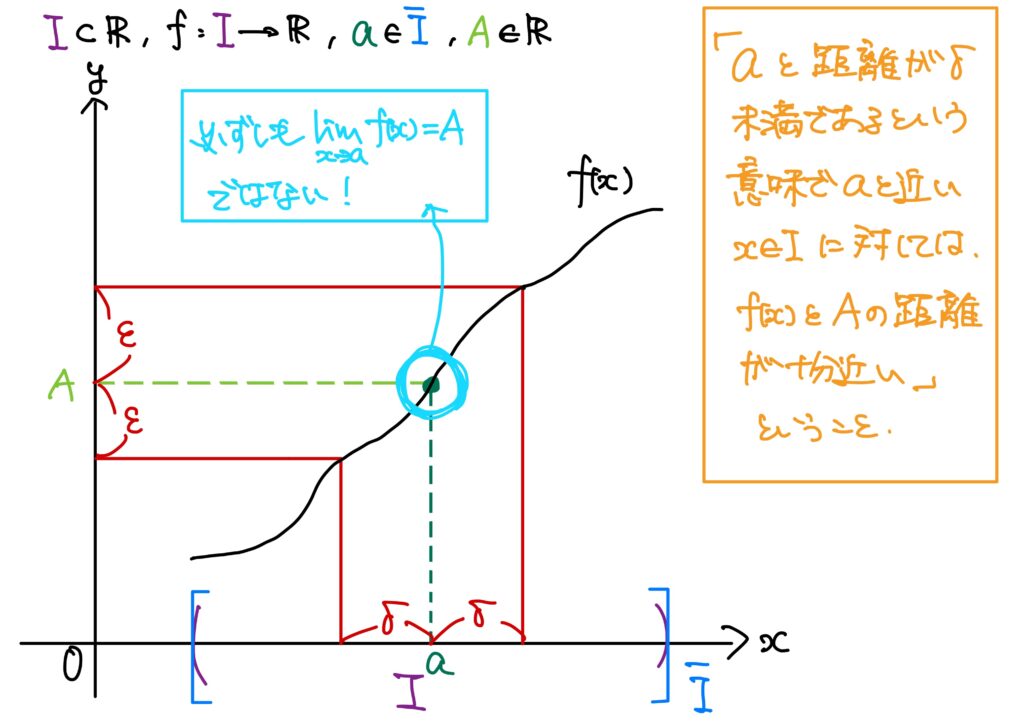
ここで「\(A\)って\(f(a)\)のことじゃねえの?」と思うかもしれないが、必ずしも一致しない。
「本当に?」と思う方は次の単元で例とともに説明するので、それまでお待ち下さい。
実際に証明してみよう!
先に挙げた例1.,2.,3.を厳密に証明してみよう!
余談とし筆者の勘所も述べるつもりなので、もしよかったらそれも読んでいただければ嬉しい。
(証明)
示したいことは、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-3|<\delta\Rightarrow |x^2-9|<\epsilon)$$
である。
すなわち、上記を満たすような\(\delta>0\)を見つけてくればよいわけである。
任意の\(\epsilon>0\)に対して、\(\delta=-3+\sqrt{9+\epsilon}\)とする。(「はぁ?なんだこれ?」と思うかもしれないが、そのときは余談を参照してください。)
すると、\(\epsilon>0\)であるため、\(\delta>0\)である。
\(|x-3|<\delta\)なる\(x\in I\)に対して、
\begin{eqnarray} |x^2-9|&=&|(x+3)(x-3)| \\
&=&|x+3|\cdot |x-3| \\
&=&|x-3+6|\cdot|x-3| \\
&<&\left(|x-3|+|6|\right)\cdot|x-3| \\
&=&|x-3|^2+6|x-3| \\
&<&\delta^2+6\delta \\
&=&(-3+\sqrt{9+\epsilon})^2+6\cdot(-3+\sqrt{9+\epsilon}) \\
&=&9-6\sqrt{9+\epsilon}+9+\epsilon-18+6\sqrt{9+\epsilon}\\
&=&\epsilon
\end{eqnarray}
従って、\(|x^2-9|<\epsilon\)が任意の\(\epsilon>0\)で成り立った。
故に、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-3|<\delta\Rightarrow |x^2-9|<\epsilon)$$
が成り立ったので、\(\displaystyle \lim_{x\to 3}x^2=9\)である。
(Q.E.D.)
この証明を読んで、「お?\(\delta\)の決め方がわかったきがするぞ?」という方はぜひ例2.の証明に挑戦してみてほしい。
(証明)
示したいことは、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-100|<\delta\Rightarrow \left|\frac{1}{x}-\frac{1}{100}\right|<\epsilon\right)$$
である。
すなわち、上記を満たすような\(\delta>0\)を見つけてくればよいわけである。
任意の\(\epsilon>0\)に対して、\(\delta=\epsilon\)とする。
すると、\(\epsilon>0\)であるため、\(\delta>0\)である。
\(|x-100|<\delta\)なる\(x\in I\)に対して、
\begin{eqnarray}
\left|\frac{1}{x}-\frac{1}{100}\right|&=&\left|\frac{100-x}{100x}\right| \\
&<&|100-x|<\delta=\epsilon
\end{eqnarray}
従って、\(\left|\dfrac{1}{x}-\dfrac{1}{100}\right|<\epsilon\)が任意の\(\epsilon>0\)で成り立った。
故に、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-100|<\delta\Rightarrow \left|\frac{1}{x}-\frac{1}{100}\right|<\epsilon\right)$$
が成り立ったので、\(\displaystyle \lim_{x\to 100}\frac{1}{x}=\frac{1}{100}\)である。
(Q.E.D.)
「ふむ。今回は\(\delta\)が\(\epsilon\)なのか。」となっていると嬉しい。
(証明)
示したいことは、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<\left|x-\frac{1}{2}\right|<\delta\Rightarrow |[x]-0|<\epsilon\right)$$
である。
すなわち、上記を満たすような\(\delta>0\)を見つけてくればよいわけである。
任意の\(\epsilon>0\)に対して、\(\delta=\epsilon\)とする。
すると、\(\epsilon>0\)であるため、\(\delta>0\)である。
ここで、任意の\(x\in I\)に対して、\([x]=0\)であることに注意する。
\(\left|x-\dfrac{1}{2}\right|<\delta\)なる\(x\in I\)に対して、
\begin{eqnarray}
|[x]-0|=|0-0|=0<\delta=\epsilon
\end{eqnarray}
従って、\(|[x]-\dfrac{1}{100}|<\epsilon\)が任意の\(\epsilon>0\)で成り立った。
故に、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall x\in I\ 0<|x-\frac{1}{2}|<\delta\Rightarrow \left|[x]-0\right|<\epsilon\right)$$
が成り立ったので、\(\displaystyle \lim_{x\to \frac{1}{2}}[x]=0\)である。
(Q.E.D.)
余談(筆者の勘所)
「どうやって\(\delta\)を見つけんだよ!」という話である。
これは実は数列のときの勘所ほとんど同じである。
例1.を解いたときの筆者の頭の中を書く。
〜〜〜筆者の頭の中〜〜〜
\(|x-3|<\delta\)を満たすような\(x\)で\(|x^2-9|<\epsilon\)が成り立つような\(\delta\)を見つけたいんだよね。
もし仮にそんな\(\delta\)があったらば、使える不等式は\(0<|x-3|<\delta\)だけだよな。
じゃあ\(|x^2-9|\)をなんとか\(\delta\)が使える形、\(|x-3|\)が出現する形に直してみるか。 \begin{eqnarray}
|x^2-9|&=&|(x+3)(x-3)| \\
&=&|x+3|\cdot |x-3| \\
&=&|x-3+6|\cdot|x-3| \\
&<&\left(|x-3|+|6|\right)\cdot|x-3| \\
&=&|x-3|^2+6|x-3| \\
&<&\delta^2+6\delta
\end{eqnarray}
なのだから、\(\delta^2+6\delta <\epsilon\)という\(\delta\)が見つけられれば嬉しい。
というより、これを満たす\(\delta\)があればいい!
ということは\(\delta^2+6\delta-\epsilon=0\)という\(\delta\)に対する2次方程式を解きゃいいんじゃんね。
解いてみると…\(\delta=-3\pm\sqrt{9+\epsilon}\)だな。
でも、\(\delta>0\)じゃなきゃいけない。
\(\epsilon>0\)だから、\(\delta=-3-\sqrt{9+\epsilon}<0\)でだめ。 \(\delta=-3+\sqrt{9+\epsilon}>0\)だ。OK。
〜〜〜筆者の頭の中おしまい〜〜〜
要は無理やりゴールから逆算している、ということである。
数列のときにも述べたが、
ということである。
結
今回は関数の収束を数学的に説明した。
直感的には
ということである。
数列の収束の証明は「ある番号」を見つけてくるのに対して、関数の収束の証明は「ある幅」を見つけてくる作業である。
次回は「関数の極限の性質」について説明する。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ1冊持っておくと良いと思います!





コメントをする