本記事の内容
本記事は「数列の発散とは数学的に何か?」および「\(\infty\)は数なのか?」ということについて解説する記事である。
本記事を読むに当たり、数列の発散のイメージを知っているとより理解しやすいと思われるので、その際は以下の記事を参照してください。
数列の発散
「数列の発散とはどういうことか」を説明するわけだが、つまりは、数列の値が”限りなく大きくなる(小さくなる)”ということを論理式であらわそう、ということである。
とはいえ、本質的には前回(数列の発散編 その1)に述べたように、どんな実数よりも大きい(小さい)ということが発散なのである。
ちなみに、数列の収束について少々復習をしておこう。
数列\(\{a_n\}_{n\in\mathbb{N}}\)が\(a\)に収束する、というのは、 どんな正の実数\(\epsilon\)を取ってきたとしても、それに対応するある番号\(N\)が存在して、\(N\)以上の自然数\(n\)(\(N\)以降の番号\(n\)に対して、\(|a_n-a|<\epsilon\)を満たすこと。
だった。
要は、「ある番号以降の\(\{a_n\}_{n\in\mathbb{N}}\)の値は\(a\)と十分近い。」ということだった。 数列の発散についても似たようなもので、 「ある番号以降の\(\{a_n\}_{n\in\mathbb{N}}\)の値はどんな実数よりも大きい」ということである。
では、明示しよう。
\(\{a_n\}_{n\in\mathbb{N}}\)が数列であるとする。
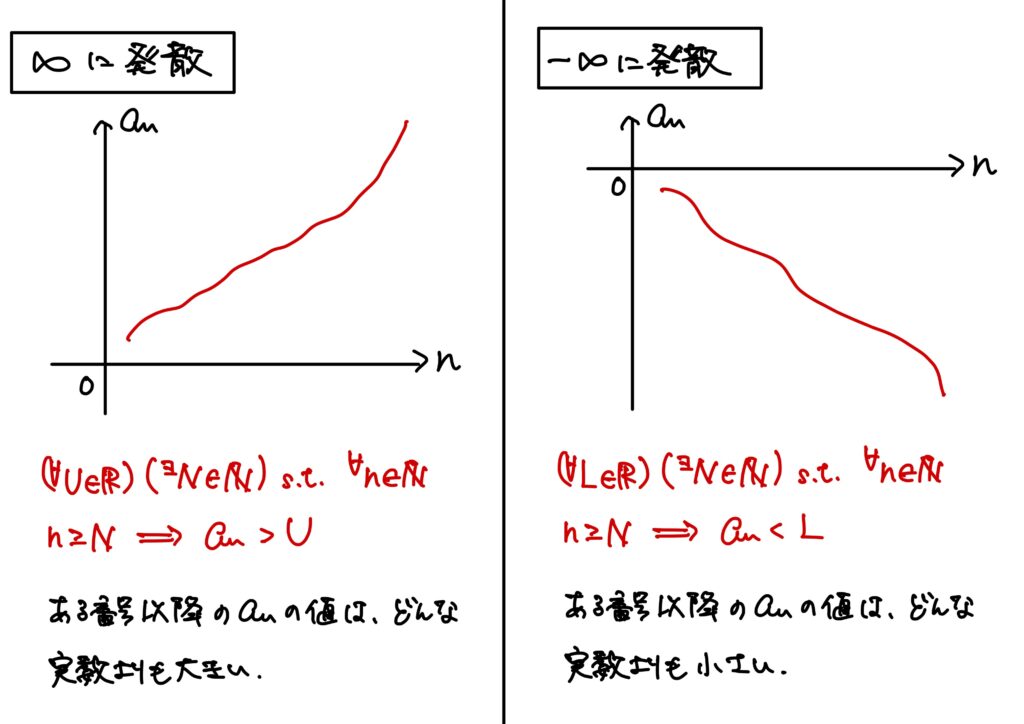
- \(\infty\)への発散 \(\{a_n\}_{n\in\mathbb{N}}\)が\(\infty\)に発散するとは、 $$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow a_n>U)$$ が成り立つ事をいう。 このことを $$\lim_{n\to\infty}a_n=\infty$$ と書く。
- \(-\infty\)への発散 \(\{a_n\}_{n\in\mathbb{N}}\)が\(-\infty\)に発散するとは、 $$(\forall L\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow a_n<L)$$ が成り立つ事をいう。 このことを $$\lim_{n\to\infty}a_n=-\infty$$ と書く。
「\(\infty\)って数なの?」
結論から言おう。
数ではない。
しかし、「どんな実数よりも大きいモノ」を表す記号で数のように扱うことができる。
「ん?」と思うかもしれないが、\(\infty\)が数であるか否かは置いておいても、少なくとも実数ではないことが分かる。
仮に\(\infty\)が実数であったとする。
すなわち、\(\infty\in\mathbb{R}\)であったとする。
このとき、\((\forall U\in\mathbb{R})\ \infty>U\)であり、かつ\(\infty\in\mathbb{R}\)なのだから、\(\infty>\infty\)が成り立つ。
しかしながら、任意の\(a,b\in\mathbb{R}\)に対して、\(a=b\)または\(a>b\)または\(a\infty\)が同時に成り立ってしまっている。
故に矛盾である。
別の言い方をしてみよう。
仮に\(\infty\in\mathbb{R}\)であったとする。
まず、任意の\(a\in\mathbb{R}\)に対して、\(a<a+1\)が成り立っており、\(a+1\in\mathbb{R}\)である。
従って、\(x=\infty+1\in\mathbb{R}\)であり、かつ\(\infty<\infty+1=x\)でなければならない。
しかしながら、これは、\(x<\infty\)かつ\(\infty<x\)が同時に成り立っている、ということになり矛盾である。
同様にして、\(-\infty\)も実数でない。
実は、\(\displaystyle\frac{1}{\infty}\)やら高校数学で出現した\(\infty\)に関わるモノは全て実数でない。
「どんな実数よりも大きいモノなんてあるんすか?」
答えは、「”モノ”があるかは(筆者は)わからないが(ごめんなさい)、少なくとも数はある。」である。
これを保証しているのが、実数の連続性を語る際に散々出現したアルキメデスの原理(「区間縮小法とアルキメデスの原理からデデキントの定理を証明しよう!」)なのである。
これをもう一度明示しておくと、
これは任意の正の実数\(a,b\)で成り立つのだから、\(a=1\)としても成り立つ。
従って、任意の正の実数\(a\)に対して、それよりも大きい自然数\(N_0\)が存在する、と言っているわけである。
したがって、どんな正の実数よりも大きい自然数が存在する、ということなのである。
こう考えると、Arichimedesさんってすげえな、と思う。
「あれ?じゃあ実数の集合って上に有界なんじゃね?」
「あら?任意の正の実数が上から抑えられてる(任意の正の実数より大きい自然数がある)のだから、実数の集合って上に有界なんじゃね?」と思うかもしれない。
しかし、そんなことはない。
有界でない(非有界と言ったりもする)。
理由は単純で「自然数だって実数じゃん。」ということである。
アルキメデスの原理から任意の正の実数\(a\)に対してそれよりも大きい\(n\in\mathbb{N}\subset\mathbb{R}\)がある。
ということは、\(n\in\mathbb{R}\)なのだから、再度アルキメデスの原理により\(n\)よりも大きい\(N\in\mathbb{N}\subset\mathbb{R}\)が存在する。
というようにこの操作は何回でもできる。
従って、ある特定の実数があって、どんな実数もその特定の実数よりも小さい、ということは起こらない。
故に実数の集合は上に有界ではない。
結
今回は数列の発散とは何か、ということを数学的に明示した。
また、無限大というモノに対する初歩も解説した。
数列が\(\infty\)に発散する、というのは、数列のある番号以降の値がどんな実数よりも大きい状態を指す。
同様に数列が\(-\infty\)に発散する、というのは、数列のある番号以降の値がどんな実数よりも小さい状態を指す。
また、無限大はどんな実数よりも大きい”モノ”であって、実数でない。
あくまで記号なのである。
次回は、数列が発散することを実際に証明してみる。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ1冊持っておくと良いと思います!




コメントをする