「初等関数の連続性を証明してみよう！(指数関数、対数関数)」【解析学の基礎シリーズ】関数の極限編 その11

本記事の内容

本記事は指数関数、対数関数、三角関数の連続性を実際に証明してみる記事である。

本記事を読むにあたり、関数の連続性について知っているとより理解が深まると思われるので、その際は以下の記事を参照してください。

「関数の連続って数学的に何？」「実際に証明してみよう！」【解析学の基礎シリーズ】関数の極限編 その５

...

for-spring.com

2022.04.05

「連続な関数の合成関数も連続な関数」【解析学の基礎シリーズ】関数の極限編 その９

...

for-spring.com

2022.04.09

序

前回の記事(【解析学の基礎シリーズ】関数の極限編 その10)で述べた初等関数のうち、多項式関数、有理関数、定数関数、無理関数は既に証明しているので、これらの証明が知りたい方はそれぞれ以下を参照してください。

• 多項式関数が連続であることの証明
• 有理関数が連続であることの証明
• 定数関数が連続であることの証明
• 無理関数が連続であることの証明

指数関数が$\mathbb{R}$で連続であることの証明

証明に入る前に流れを説明する。

• (ステップ1)：指数法則と、「積の極限は極限の積と等しい」という事実を使って示したいことを簡略化する。
  $x\to b$ではなく、実は$x\to0$のときに$a^x\to1$であることを示せばOKということが分かる。
• (ステップ2)：$x\to0$のときに$a^x\to1$であることを示す。
• おしまい。

(証明)

正直に証明するならば、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x-b|<\delta\Rightarrow |a^x-a^b|<\epsilon)$$
を示せば良いのだが、今回は「指数法則」と「積の極限は極限の積」(【解析学の基礎シリーズ】関数の極限編 その3)を使うことによって、より簡単に証明ができる。

(ステップ1)
$$\begin{eqnarray} \lim_{x\to b}a^x&=&\lim_{x\to b}a^{b+(x-b)}\\ &=&\lim_{x\to b}\left(a^b\cdot a^{x-b} \right)\\ &=&\left(\lim_{x\to b}a^b\right)\cdot \left(\lim_{x\to b}a^{x-b}\right) (積の極限は極限の積だから。)\\ &=&a^b\cdot \left(\lim_{x\to b}a^{x-b}\right) (定数関数の極限はその定数に収束するから。) \end{eqnarray}$$

であるから、$\displaystyle\lim_{x\to b}a^{x-b}=1$であれば良い。
すなわち、
$$\lim_{x\to 0}a^x=1$$
が成り立てば良い。

実際、$\displaystyle A=\lim_{x\to b}a^{x-b}\Rightarrow A=\lim_{x\to 0}a^x$が成り立つからである。
なぜならば、$\displaystyle A=\lim_{x\to b}a^{x-b}$としたとき、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x-b|<\delta\Rightarrow |a^x-A|<\epsilon)$$
が成り立っている。
このとき、$y=x-b$とすると$|y|=|x-b|\in\mathbb{R}$であり、$0<|y|<\delta$である。
今、$|a^{x-b}-A|<\epsilon$が任意の$\epsilon>0$で成り立っているのだから、$|a^y-A|<\epsilon$も成り立っている。
これはまさに$\displaystyle A=\lim_{x\to 0}a^x$である。

(ステップ2)

(補題2.の証明)
示したいことは、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x|<\delta\Rightarrow |a^x-1|<\epsilon)$$
である。
要は、上記を満たす$\delta$を見つけてきなさいということである。
$a$について2つの場合に分ける。
①$a>1$のとき
任意の$\epsilon>0$に対して、$\displaystyle\epsilon_1=\min\left\{\epsilon,\frac{1}{2}\right\}$とすると、$0<\epsilon\leq \dfrac{1}{2}$
が成り立つ。
ここで、
$$\delta=\min\left\{ -\log_a(1-\epsilon_1),\log_a(1+\epsilon_1) \right\}$$
とする。(※余談1参照)
このとき$\delta>0$である。
実際、$a>1$であり、$\epsilon_1\leq\dfrac{1}{2}<1$により、$\log_a(1-\epsilon_1)<0$だからである。
さて、$|x|<\delta$なる$x\in\mathbb{R}$に対して、
$$\begin{eqnarray} |x|<\delta&\Leftrightarrow&-\delta<x<\delta\\ &\Leftrightarrow&\left(\log_a(1-\epsilon_1)<x<-\log_a(1-\epsilon_1)\right)または\left(-\log_a(1+\epsilon_1)<x<\log_a(1+\epsilon_1)\right) \end{eqnarray}$$
$\delta$は$-\log_a(1-\epsilon_1),\log_a(1+\epsilon_1)$のうち小さい方を採用するのだから、$x$の範囲としては狭いような$\delta$を採用することになる。
故に、
$$\begin{eqnarray} |x|<\delta&\Rightarrow&\log_a(1-\epsilon_1)<x<\log_a(1+\epsilon_1)\\ &\Rightarrow&1-\epsilon_1<a^x<1+\epsilon_1\\ &\Rightarrow&-\epsilon_1<a^x-1<\epsilon_1\\ &\Rightarrow&|a^x-1|<\epsilon_1 \end{eqnarray}$$
ここで、$\displaystyle\epsilon_1=\min\left\{\epsilon,\frac{1}{2}\right\}$だったことを思い出すと、$|a^x-1|<\epsilon_1<\epsilon$である。
従って、$a>1$のときは
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x|<\delta\Rightarrow |a^x-1|<\epsilon)$$
が成り立った。

故に
$$\begin{eqnarray} |x|<\delta&\Rightarrow&\log_a(1-\epsilon_1)<\log_a(1+\epsilon_1)\\ &\Rightarrow&1-\epsilon_1<a^x<1+\epsilon_1\\ &\Rightarrow&-\epsilon_1<a^x-1<\epsilon<1\\ &\Rightarrow&|a^x-1|<\epsilon_1 \end{eqnarray}$$
ここで、$\displaystyle\epsilon_1=\min\left\{\epsilon,\frac{1}{2}\right\}$だったことを思い出すと、$|a^x-1|<\epsilon_1<\epsilon$である。
従って、$a>1$のときは
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x|<\delta\Rightarrow |a^x-1|<\epsilon)$$
が成り立った。

②$0<a<1$のとき
$b=\dfrac{1}{a}$とすることで、$b>1$となるから、先の場合と同様の議論になる。
従って、
$$\lim_{x\to0}b^x=1$$
が成り立つ。
すなわち、
$$\begin{eqnarray} \lim_{x\to 0}a^x&=&\lim_{x\to0}\left(\frac{1}{b^x}\right)\\ &=&\frac{\displaystyle\lim_{x\to0}1}{\displaystyle\lim_{x\to 0}b^x}\\ &=&\frac{1}{1}\\ &=&1 \end{eqnarray}$$
故にこの場合も、 $$\lim_{x\to0}a^x=1$$ が成り立つ。

• $a=1$のときは、$\displaystyle\lim_{x\to 0}a^x=\lim_{x\to 0}1=1$により成り立つ。

(Q.E.D.)

従って、補題2.が成り立ったので、命題1.が成り立つ。
(Q.E.D.)

余談1($\delta$のとり方)

やはり、難しいのは$\delta$のとり方である。
さらに今回は$\epsilon$についても若干特殊なことをした。
今回は補題2.の証明の①$a>1$のときを例に取って、筆者がどう考えたかを伝える。

〜〜〜〜〜〜〜〜〜〜筆者の頭の中〜〜〜〜〜〜〜〜〜〜
$|x|<\delta$ならば$|a^x-1|<\epsilon$が成り立つような$\delta>0$が仮にあったとしよう。
すなわち
$$|x|<\delta\Leftrightarrow -\delta<x<\delta$$
が成り立つということだ。
目標としては$|a^x-1|<\epsilon$を示したいのだから、$\delta$を逆算するためにこの式を変形してみる。
$$\begin{eqnarray} |a^x-1|<\epsilon&\Leftrightarrow&-\epsilon<a^x-1<\epsilon\\ &\Leftrightarrow&1-\epsilon<a^x<1+\epsilon \end{eqnarray}$$
仮に$1-\epsilon>0$ならば、真数条件を満たすから$\log_a(1-\epsilon)<x<\log_a(1+\epsilon)$が成り立つ。
ということは$\delta$として$\log_a(1-\epsilon)$か$\log_a(1+\epsilon)$の小さい方をを取れば良い。
しかし$a>1$だから$\log_a(1-\epsilon)<0$であるし、ここには注意しなければならない。

まずは$\epsilon$について考えてみる。
$\epsilon>0$は任意の実数なのだから、必ずしも$1-\epsilon>0$ではない。
では、必ず$1-\epsilon>0$となるように$\epsilon>0$を書き直す。
$1-\epsilon>0$となれば良いのだから、$1>\epsilon>0$であれば良い。
仮に$\epsilon=\dfrac{1}{2}$(実際は$\dfrac{1}{3}$でも$\dfrac{1}{100}$でも良い)であればよい。
では、任意の$\epsilon>0$と$\dfrac{1}{2}$のうち、小さい方を$\epsilon_1$と名付ける。
こうすれば、$\dfrac{1}{2}$より大きい正の実数は$\epsilon$で表現でき、$\dfrac{1}{2}$より小さい正の実数も$\epsilon$で表現できる。
さらに$\epsilon_1$は常に$1-\epsilon_1>0$である。

次は$\delta$。
先程決めた$\epsilon_1$をつかうと、$\delta$の候補としては$\log_a(1-\epsilon_1)$か$\log_a(1+\epsilon_1)$の小さい方だが、$\log_a(1-\epsilon_1)<0$だから、$-\log_a(1-\epsilon_1)>0$である。
従って、$-\log_a(1-\epsilon_1)$か$\log_a(1+\epsilon_1)$の小さい方を$\delta$とすれば$\delta>0$であり、かつ$|x|<\delta$だ。
実際、$\delta=-\log_a(1-\epsilon_1)$ならば、$-\log_a(1-\epsilon_1)<\log_a(1+\epsilon_1)$だから、$-\delta<x<\delta\Rightarrow \log_a(1-\epsilon)<x<\log_a(1+\epsilon)$が成り立つ。
一方$\delta=\log_a(1+\epsilon_1)$ならば、$\log_a(1+\epsilon_1)<-\log_a(1-\epsilon_1)$であるから、$-\delta<x<\delta\Rightarrow \log_a(1-\epsilon)<x<\log_a(1+\epsilon)$が成り立つ。
従って
$$\delta=\min\left\{ -\log_a(1-\epsilon_1),\log_a(1+\epsilon_1) \right\}$$
である。
〜〜〜〜〜〜〜〜〜〜筆者の頭の中おしまい〜〜〜〜〜〜〜〜〜〜〜

対数関数が$\mathbb{R}_{>0}$で連続であることの証明

対数関数の場合は指数関数よりも正直な証明方法である。
ただし、指数と対数の関係は使う。
とはいえ、むしろ指数と対数の関係しか使わないという点においては誠にシンプルである。

(証明)

示したいことは
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x-b|<\delta\Rightarrow |\log_ax-\log_ab|<\epsilon)$$
である。

①$a>1$のとき
$c=\log_ab$とすると、$b=a^c$が成り立つ。
任意の$\epsilon>0$に対して、
$$c-\epsilon<c<c+\epsilon$$
が成り立つ。
加えて、$b’=a^{c-\epsilon}$、$b”=a^{c+\epsilon}$とおくと、$a>1$のときは
$$b'<b<b”$$
が成り立つ。

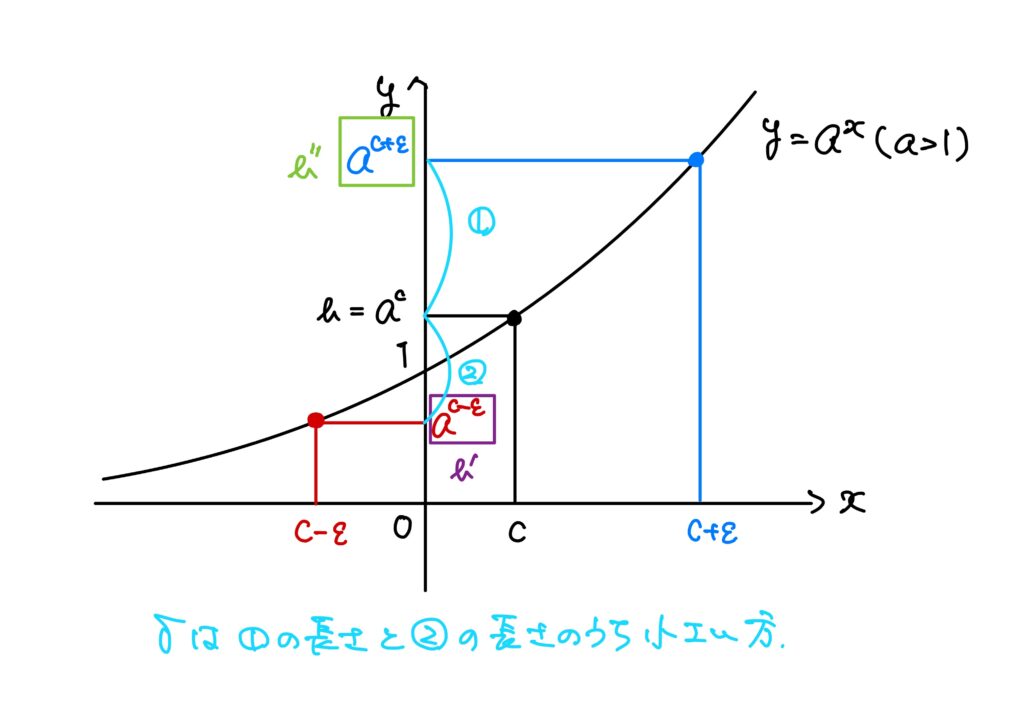
ここで、
$$\delta=\min\left\{ b”-b,b-b’ \right\}$$
とすれば、$\delta>0$である。(余談2参照)
$|x-b|<\delta$なる$x\in\mathbb{R}$に対して、
$$\begin{eqnarray} |x-b|<\delta&\Rightarrow&b'<x<b”\\ &\Rightarrow&\log_ab'<\log_ax<\log_ab”\\ &\Rightarrow&c-\epsilon<\log_ax<c+\epsilon\\ &\Rightarrow&\log_ab-\epsilon<\log_ax<\log_ab+\epsilon\\ &\Rightarrow&|\log_ax-\log_ab|<\epsilon \end{eqnarray}$$
従って、$a>1$のときは$\displaystyle\lim_{x\to\ b}\log_ax=\log_ab$が成り立つ。

②$0<a<1$のとき
$a>1$と殆ど同じ方法で証明できる。
$c=\log_ab$とすると、$b=a^c$が成り立つ。
任意の$\epsilon>0$に対して、
$$c-\epsilon<c<c+\epsilon$$
が成り立つ。
加えて、$b’=k^{c-\epsilon}$、$b”=k^{c+\epsilon}$とおくと、$0<a<1$のときは
$$b”<b<b’$$
が成り立つ。
ここで、
$$\delta=\min\left\{ b’-b,b-b” \right\}$$
とすれば、$\delta>0$である。
$|x-b|<\delta$なる$x\in\mathbb{R}$に対して、
$$\begin{eqnarray} |x-b|<\delta&\Rightarrow&b”<x<b’\\ &\Rightarrow&\log_ab”<\log_ax<\log_ab’\\ &\Rightarrow&c-\epsilon<\log_ax<c+\epsilon\\ &\Rightarrow&\log_ab-\epsilon<\log_ax<\log_ab+\epsilon\\ &\Rightarrow&|\log_ax-\log_ab|<\epsilon \end{eqnarray}$$
従って、$0<a<1$のときも$\displaystyle\lim_{x\to\ b}\log_ax=\log_ab$が成り立つ。

以上から、 $$\lim_{x\to\ b}\log_ax=\log_ab$$ である。
(Q.E.D.)

余談2($\delta$のとり方)

今回も命題1.の①$a>1$のときを例にとる。

〜〜〜〜〜〜〜〜〜〜筆者の頭の中〜〜〜〜〜〜〜〜〜〜

指数関数と同じようにやってみる。
$|x-b|<\delta$ならば$|\log_ax-\log_ab|<\epsilon$が成り立つような$\delta>0$が仮にあったとする。
$$|x|<\delta\Leftrightarrow -\delta<x<\delta$$
が成り立つということだ。
目標としては$|\log_ax-\log_ab|<\epsilon$を示したいのだから、$\delta$を逆算するためにこの式を変形してみる。
$$\begin{eqnarray} |\log_ax-\log_ab|<\epsilon&\Leftrightarrow&-\epsilon<\log_ax-\log_ab<\epsilon\\ &\Leftrightarrow&\log_ab-\epsilon<\log_ax<\log_ab+\epsilon \end{eqnarray}$$
今、$a>1$なのだから、
$$\begin{eqnarray} \log_ab-\epsilon<\log_ax<\log_ab+\epsilon&\Rightarrow&a^{\log_ab-\epsilon}<a^{\log_ax}<a^{\log_ab+\epsilon}\\ &\Leftrightarrow&a^{\log_ab-\epsilon}<x<a^{\log_ab+\epsilon} \end{eqnarray}$$
これが成り立っていれば良い。
従って候補は$a^{\log_ab-\epsilon}$と$a^{\log_ab+\epsilon}$のうち、小さい方だな。
しかしこれは記号が乱立しているため新しい記号を導入する。
〜〜〜〜〜〜〜〜〜〜筆者の頭の中おしまい〜〜〜〜〜〜〜〜〜〜

結

今回は指数関数と対数関数が$\mathbb{R}$で連続であることを証明した。
多項式関数やらとは少々毛色が違ったのだが、指数と対数の法則を”うまく”使うことで証明ができる。

【解析学の基礎シリーズ】関数の極限 その7および【解析学の基礎シリーズ】関数の極限編 その9で述べたように、連続な関数の和・差・積・商も連続な関数(商だけは特別)、連続な関数の合成関数もまた連続な関数であるから、前回の記事(【解析学の基礎シリーズ】関数の極限編 その10)で列挙した例

• 例4. $g:\mathbb{R}\to\mathbb{R}$、$g(x)=2^{\frac{x}{3}}$
  これは、$f(x)=x^{\frac{1}{3}}$と$g(x)=2^x$の合成関数。
• 例6. $g_3:\mathbb{R}_{>0}\to\mathbb{R}$、$\displaystyle g_3(x)=\frac{\log x}{x^2}$
  これは、$f(x)=\log x$と$g(x)=x^2$の商を取った関数。

が連続な関数であることが分かる。

次回は三角関数と逆三角関数がそれぞれ特定の範囲で連続であることを示す。

乞うご期待！質問、コメントなどお待ちしております！

この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください！
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ１冊持っておくと良いと思います！