ユークリッドの互除法(大きい数の最大公約数)

本記事の内容

本記事は大きい数の最大公約数を求める手法として有用なユークリッドの互除法について解説する記事です。

本記事を読むに当たり、最大公約数について知っている必要があるため、以下の記事も合わせてご覧ください。

整数の積=最大公約数×最小公倍数

...

for-spring.com

2023.02.22

最小公倍数、最大公約数のちょっとした復習

最小公倍数、最大公約数とは以下でした。

詳しくは、【代数学の基礎シリーズ】初等整数論編 その3を御覧ください。

ちなみに、最小公倍数は公倍数の最小値ではなく、公倍数に絶対値をとった数から\(0\)を除いた整数の最小値でしたね。

\(\gcd(a,b)=1\)かつ\(bc\)が\(a\)で割り切れるならば、\(c\)が\(a\)で割り切れる。

最大公約数が\(1\)であるときには、その性質を使うことで「どの整数がどの整数を割り切る」のかが明瞭になります。

定理1.の証明

まず、次の事実を使います。

定理2.の証明は【代数学の基礎シリーズ】初等整数論編 その3を御覧ください。

今、\(\gcd(a,b)=1\)ですので、定理2.から\(a\)と\(b\)の最小公倍数は\(ab\)です。
すなわち\({\rm lcm}(a,b)=ab\)です。
さらに、仮定から\(bc\)は\(a\)で割り切れる為、\(bc\)は\(a\)の倍数です。
もちろん、\(bc\)は\(b\)で割り切れる為、\(bc\)は\(b\)の倍数でもあります。
すなわち、\(bc\)は\(a\)と\(b\)の公倍数です。

ここで、次の事実を使います。

定理3.の証明は【代数学の基礎シリーズ】初等整数論編 その3を御覧ください。

今、\({\rm lcm}(a,b)=ab\)であるので、定理3.から\(bc\)は\(ab\)の倍数です。
したがって、
$$
\frac{bc}{ab}=\frac{c}{a}\in\mathbb{Z}
$$
です。
すなわち、\(c\)は\(a\)で割り切れます。

定理1.の証明終わり

大きい数の最大公約数はどのように求めるか？(ユークリッドの互除法)

最大公約数自体難しい概念ではありませんが、例えば次のような問題が出たとしましょう。

確かに、\(35187368436\)の約数をすべて求め、その後\(6543983986\)の約数をすべて求めて、その中で共通な約数を見つけて、その中で最大のものは…とすれば求まります。
しかし非常に面倒です。

時としてこういった問題が出ます。
このような問題はま正直に解くと非常に時間がかかってしまいます。

これを整数の性質を使うことで、分かりやすく簡単に求めようというのがユークリッドの互除法です。

先に少々ネタバラシをしておくと、ユークリッドの互除法を1回行うだけで直ちに分かりやすく最大公約数が求まるわけではなく、数回行うことでどんどん分かりやすくして最大公約数を求めます。

定理0.(ユークリッドの互除法)の証明

$$
a=qb+r\quad (0\leq r<b)\tag{1}
$$
とし、\(m=\gcd(a,b)\)とします。
このとき、\(m\)は\(a\)と\(b\)の約数ですので、
$$
(\exists k_1,k_2\in\mathbb{Z})\ {\rm s.t.}\ a=mk_1\land b=mk_2
$$
です。
これを(1)に代入すれば、
\begin{eqnarray}
a=qb+r&\Longleftrightarrow&mk_1=q\cdot mk_2+r\\
&\Longleftrightarrow&mk_1-qmk_2=r\\
&\Longleftrightarrow&m\left( k_1-qk_2\right)=r
\end{eqnarray}
となるため、\(m\)は\(r\)、すなわち\(a-qb\)の約数です。
\(m=\gcd(a,b)\)ですので、\(m\)は\(b\)の約数でもあります。
つまり、\(m\)は\(a-qb\)と\(b\)の公約数です。
ここで、次の事実を使います。

定理4.の証明は【代数学の基礎シリーズ】初等整数論編 その3を御覧ください。

定理4.から、\(m\)は\(\gcd(a-qb,b)\)の約数です。
したがって、\(m\leq \gcd(a-qb,b)\)、すなわち\(\gcd(a,b)\leq\gcd(a-qb,b)\)です。

逆に、\(m\)が\(a-qb\)と\(b\)を割り切る(つまり、\(m\)が\(a-qb\)と\(b\)の公約数)とすると、
$$
(\exists t_1,t_2\in\mathbb{Z})\ {\rm s.t.}\ a-qb=mt_1\land b=mt_2
$$
であるため、\(a-q\cdot mt_2=mt_1\)だから、\(a=m\left( t_1-qt_2\right)\)となります。
したがって、\(m\)は\(a\)と\(b\)の公約数です。
したがって、\(\gcd(a-qb,b)\leq m=\gcd(a,b)\)となります。

いじょうのことから、\(\gcd(a,b)=\gcd(a-qb)\)となります。

定理0.の証明終わり

\(a,b\in\mathbb{Z}\)に対して、\(a\)を\(b\)で割った余りを\(c\)としましょう。
すると、ユークリッドの互除法から、\(\gcd(a,b)=\gcd(b,c)\)です。
次に、\(b\)を\(c\)で割った余りを\(d\)とすれば、これもユークリッドの互除法から\(\gcd(b,c)=\gcd(c,d)\)です。
このように操作を続けていけば、\(a>b>c>d>\cdots\)というようになります(後述します)。
余りは必ず\(0\)以上ですから、この操作を続けていけば、有限回の試行で余りは\(0\)になります。
今、\(c\)を\(d\)で割った余りが\(0\)、すなわち\(d\)が\(c\)を割り切るとしましょう。
すると、\(\gcd(c,d)=\gcd(d,0)=d\)となります。
すなわち、\(d=\gcd(a,b)\)です。

これがユークリッドの互除法の最初に述べた「数回行う」という意味になります。

ユークリッドの互除法を使ってみる。

では、実際にユークリッドの互除法を使ってみましょう。

具体的な問題の前に…

本節では、\(a,b\in\mathbb{Z}\)の最大公約数\(\gcd(a,b)\)をユークリッドの互除法で求めてみます。
\(a=a_0\)、\(b=b_0\)とし、割り算定理(剰余の定理)を使っていきます。

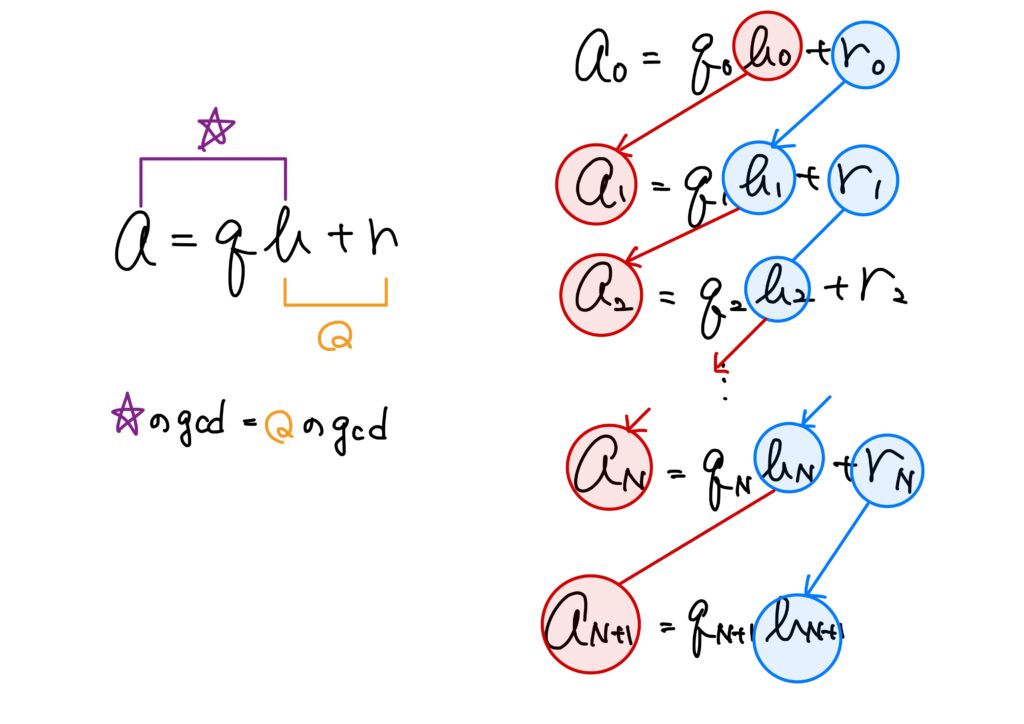
これを数学的に書けば次になります。
\begin{eqnarray}
&&a_0=q_0b_0+r_0,\quad 0\leq r_0<b_0,\quad a_1=b_0,\ b_1=r_0\\
&&a_1=q_1b_1+r_1,\quad 0\leq r_1<b_1,\quad a_2=b_1,\ b_2=r_1\\
&&a_2=q_2b_2+r_2,\quad 0\leq r_2<b_2,\quad a_3=b_2,\ b_3=r_2\\
&&\qquad \qquad\vdots\\
&&a_N=q_Nb_N+r_N,\quad 0\leq r_N<b_N,\quad a_{N+1}=b_N,\ b_{N+1}=r_N\\
&&a_{N+1}=q_{N+1}b_{N+1}+0
\end{eqnarray}
つまり、\(b_{N+1}=r_N\)は\(a_{N+1}=b_N\)を割り切ります。
上式を見ると、たしかに
$$
b_0>r_0=b_1>r_1=b_2>r_2=b_3>\cdots=b_N>r_N=b_{N+1}>r_{N+1}=0
$$
となっており、つまりは
$$
r_0>r_1>r_3>\cdots>r_N>r_{N+1}=0
$$
ということになります。

実際に解いてみる。(例1)

\(\gcd(39,15)\)を計算してみましょう(上の式において\(a=39\)、\(b=15\))。

\begin{eqnarray}
39&=&15\times 2+9\\
15&=&9\times 1+6\\
9&=&6\times1+3\\
6&=&3\times 2+0
\end{eqnarray}

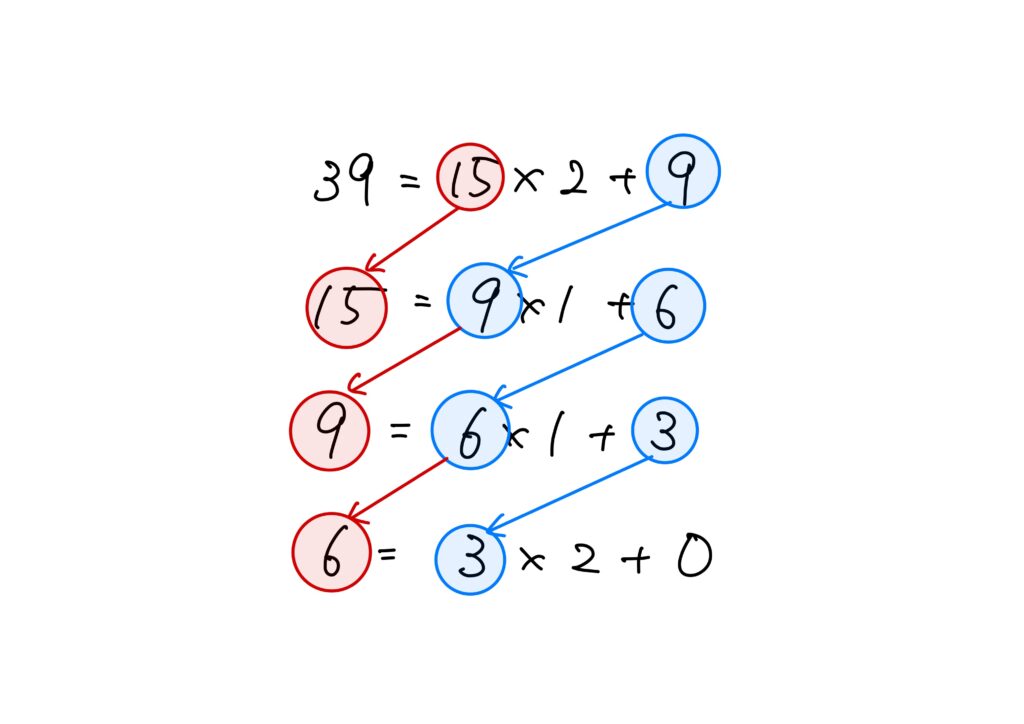
故に、\(\gcd(39,15)=3\)です。

実際に解いてみる。(例2)

最初に挙げた大きい数を扱ってみましょう(ユークリッドの互除法を使っても手間がかかりますが…)。
\begin{eqnarray}
35187368436&=&6543983986\times5+2467448506\\
6543983986&=&2467448506\times2+1609086974\\
2467448506&=&1609086974\times1+858361532\\
1609086974&=&858361532\times1+750725442\\
858361532&=&750725442\times1+107636090\\
750725442&=&107636090\times6+104908902\\
107636090&=&104908902\times1+2727188\\
104908902&=&2727188\times38+1275758\\
2727188&=&1275758\times2+175672\\
1275758&=&175672\times7+46054\\
175672&=&46054\times3+37510\\
46054&=&37510\times1+8544\\
37510&=&8544\times4+3334\\
8544&=&3334\times2+1876\\
3334&=&1876 \times1+1458\\
1876&=&1458 \times1+418\\
1458&=&418\times3+204\\
418&=&204\times2+10\\
204&=&10\times20+4\\
10&=&4\times2+2\\
4&=&2\times2+0
\end{eqnarray}
故に、
$$
\gcd(35187368436,6543983986)=2
$$
とわかります。

ユークリッドの互除法は3つ以上の整数の最大公約数を求める事もできる。

時として3つ以上の整数の最大公約数を求めるという状況も生まれます。
しかし、結局は2つの整数の最大公約数を求めるユークリッドの互除法に帰着されます。

\(a,b,c,\cdots,l\in\mathbb{Z}\)の最大公約数を求めるとしましょう。
このとき、\(a,b,c,\cdots,l\)の中で\(a\)が一番小さいとしましょう。
\(a\)で\(b,c,\cdots,l\)を割って、その余りを\(b^\prime,c^\prime,\cdots,l^\prime\)と書いたとします。
すると、2つの整数の場合のユークリッドの互除法と同様にして、
$$
\gcd(a,b,c,\cdots,l)=\gcd(a,b^\prime,c^\prime,\cdots,l^\prime)
$$
が成り立ちます。

\(b^\prime,c^\prime,\cdots,l^\prime\)の中に\(0\)があれば、それは\(\gcd()\)の中から除外してOKです。
実際、
\(\gcd(k,0)=k\)と同様にして
$$
\gcd(a_1,\cdots,a_{i-1},0,a_{i+1},\cdots,a_n)=\gcd(a_1,\cdots,a_{i-1},a_{i+1},\cdots,a_n)
$$
が成り立つからです。

さて、今
$$
\gcd(a,b,c,\cdots,l)=\gcd(a,b^\prime,c^\prime,\cdots,l^\prime)
$$
が成り立っているわけですが、今度は\(\gcd(a,b^\prime,c^\prime,\cdots,l^\prime)\)に同じ操作を行います。
このとき、\(b^\prime,c^\prime,\cdots,l^\prime\)は\(b,c,\cdots,l\)を\(a\)で割った余りですから、どれも\(a\)より小さいです。
故に、\(b^\prime,c^\prime,\cdots,l^\prime\)の中で最も小さい数を選び、再度その数で\(b^\prime,c^\prime,\cdots,l^\prime\)を割った余りを\(b^{\prime\prime},c^
{\prime\prime},\cdots,l^{\prime\prime}\)とします。

この操作をつづければ、毎回\(\gcd()\)内の最大値が小さくなっていきますから、次第にあまりが\(0\)であるようなものが出てきて、ついには\(\gcd(k,0)\)の形になります。

以上のことから、結局3つ以上の場合でもユークリッドの互除法は2つの場合に帰着されます。

例えば、
$$
\gcd(629,391,255)=\gcd(119,-119,255)=\gcd(119,17)=17
$$
という具合です。

皆様のコメントを下さい！

ユークリッドといえば、『原論』が有名です。
筆者は学部生の頃、ユークリッド幾何学を学んだとき「ユークリッド幾何学ってゴリゴリの論理の話なんだ」と驚き、「人類は紀元前300年頃にこのようなことを考えていたんだ」と感動しました。
そこで、「原論を読んでみるか」と思い(もちろん、原典はギリシャ文字で書かれているので読めませんが)、現代版の原論を読みました。

皆様は、古い本は読まれますか？
もしくは読みたいと思っている本はありますか？
ぜひコメントで教えて下さい！

結

今回は大きい数の最大公約数を求める手法としてユークリッドの互除法を解説しました。
ユークリッドの互除法は誠に有用です。
今や高校数学で学ぶ内容ですが、なぜユークリッドの互除法が成り立つのか？と考えたとき、実は核の部分では「割り算定理(剰余の定理)が成り立っているから」ということになります。
割り算定理の記事でも述べましたが、これは小学校で出現する内容です。
そう考えると、やはり数学はつながっているなと感じざるを得ません。

次回は3つ以上の整数の最小公倍数を求める方法について解説します。

乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ１週間以内にお答えします。
(難しかったらもう少しかかるかもしれませんが…)

初等整数論について、以下の書籍をオススメします！