区間縮小法⇒デデキントの定理

本記事の内容
「区間縮小法+アルキメデスの原理ならばデデキントの定理」の証明
実数の連続性との関係性
結

本記事の内容

本記事は区間縮小法(区間縮小の原理)とアルキメデスの原理からデデキントの定理を証明する記事です。

この記事を読むにあたり、区間縮小法を知っている必要があるため、以下の記事も合わせて御覧ください。

「区間縮小法+アルキメデスの原理ならばデデキントの定理」の証明

定理. 区間縮小の原理+アルキメデスの原理$\Rightarrow$デデキントの定理

アルキメデスの原理の証明は道中(使う場所)で行います。
また、デデキントの定理は以下でした。

デデキントの定理 実数の集合$\mathbb{R}$の任意の切断$(A,B)$に対して、ある実数$r$が存在して、次の2つのいずれか一方が成り立つ。

$A$には最大値が無く、$B$には最小値$r$がある。
$A$には最大値$r$があり、$B$には最小値がない。

デデキントの定理の証明は【解析学の基礎シリーズ】実数の連続性編その2を御覧ください。

定理の証明に入る前に、証明の流れを説明します。

区間縮小の原理を満たす区間の列を作る。
- (ステップ1-1) 実数の切断$(A,B)$から区間縮小の原理を満たすような縮小する区間(どんどん小さくなる区間)の列$\{I_n\}_{n\in\mathbb{N}}$を作る。
- (ステップ1-2) 作った区間から単調増加数列$\{a_n\}_{n\in\mathbb{N}}$と単調減少数列$\{b_n\}_{n\in\mathbb{N}}$を得る。
  作った区間の左端からなる数列を$\{a_n\}_{n\in\mathbb{N}}$、右端からなる数列を$\{b_n\}_{n\in\mathbb{N}}$とすることで、$\{a_n\}_{n\in\mathbb{N}}$は単調増加、$\{b_n\}_{n\in\mathbb{N}}$は単調減少数列となる。
- (ステップ1-3) 任意の自然数$n$に対して区間$I_n$の長さ$|b_n-a_n|$をからなる数列$\{|b_n-a_n|\}_{n\in\mathbb{N}}$が$\displaystyle\lim_{n\to\infty}|b_n-a_n|=0$を満たすことを示す。
  これを示すために、アルキメデスの原理(補題6.)と、とある数列が$0$に収束するという事実を使う！(これらは定理.の証明の道中で証明します。)
- これで区間縮小の原理の仮定を満たすような区間と数列を作ることができた。
デデキントの定理を導く。

$\displaystyle\bigcap_{n\in\mathbb{N}}I_n$の要素$c$を任意に取ってきたとき、$c$が$A$の最大値か$B$の最小値かのいずれか一方であることを示す。
- (ステップ2-1) $\displaystyle\bigcap_{n\in\mathbb{N}}I_n$の要素$c$を任意に取ってくる。
  1.で作った区間の列は区間縮小の原理を満たすのだから、$\displaystyle\bigcap_{n\in\mathbb{N}}I_n$の要素$c$について考える。
- (ステップ2-2) $c\in A$のとき、$c$は$A$の最大値であり、同時に$B$には最小値が存在しない事を示す。
- (ステップ2-3) $c\in B$のとき、$c$は$B$の最小値であり、同時に$A$には最大値が存在しない事を示す。

証明

示したいことは、区間縮小の原理を仮定したとき、任意の実数の切断$(A,B)$に対して、

$A$には最大値が無く、$B$には最小値がある。
$A$には最大値があり、$B$には最小値がない。

のいずれか一方のみが成り立つことです。

(ステップ1-1)
$(A,B)$を任意の実数の切断とします。
このとき、$A$から要素$a$を、$B$から要素$b$を任意にとります。
すなわち、$a\in A$および$b\in B$を任意に取ります。
そして、この$a,b$を両端とする区間$[a,b]$に$I_0$と名前をつけます。
すなわち、$I_0=[a,b]$とします。

(ステップ1-2)
さて、$a$と$b$の中間にある数$\displaystyle\frac{a+b}{2}$(有理数とは限りません)は、$(A,B)$が切断であることから$A$および$B$のいずれか一方の要素です。

$\displaystyle \frac{a+b}{2}\in A$のとき
$$a_1=\frac{a+b}{2},\ b_1=b$$
$\displaystyle \frac{a+b}{2}\in B$のとき
$$a_1=a,\ b_1=\frac{a+b}{2}$$

と置くことによって、区間$I_1=[a_1,b_1]$の左端$a_1$は$A$の要素であり、右端$b_1$は$B$の要素です。
さらに、区間$I_1$は区間$I_0$の部分集合であり、区間$I_1$は区間$I_0$の右半分($\displaystyle \frac{a+b}{2}\in A$のとき)かまたは左半分($\displaystyle \frac{a+b}{2}\in B$のとき)です。
加えて、区間$I_1$の幅は$\displaystyle b_1-a_1=\frac{1}{2}(b-a)$です。

同様に

$\displaystyle \frac{a_1+b_1}{2}\in A$のとき
$$a_2=\frac{a_1+b_1}{2},\ b_2=b_1$$
$\displaystyle \frac{a_1+b_1}{2}\in B$のとき
$$a_2=a_1,\ b_2=\frac{a_1+b_1}{2}$$

と置くことによって、区間$I_2=[a_2,b_2]$の左端$a_2$は$A$の要素であり、右端$b_2$は$B$の要素です。
さらに、区間$I_2$は区間$I_1$の部分集合であり、区間$I_2$は区間$I_1$の右半分($\displaystyle \frac{a_1+b_1}{2}\in A$のとき)かまたは左半分($\displaystyle \frac{a_1+b_1}{2}\in B$のとき)です。
加えて、区間$I_2$の幅は$\displaystyle b_2-a_2=\frac{1}{4}(b-a)$です。

この操作を続ける事によって、
$$I_0\supset I_1\supset I_2\supset \dots I_n\supset \dots$$
という縮小する区間の列と、
$$I_n=[a_n,b_n],\ b_n-a_n=\frac{1}{2^n}(b-a)$$
を得ることができます。
また、このとき、数列$\{a_n\}_{n\in\mathbb{N}}$は上に有界な単調増加数列であり、数列$\{b_n\}_{n\in\mathbb{N}}$は下に有界な単調減少数列です。
実際、
$$a_{n+1}=\begin{cases}
a_n \\
\displaystyle\frac{a_n+b_n}{2}
\end{cases}$$
であるので、
$$a_{n+1}-a_n=\begin{cases}
a_n-a_n=0 \\
\displaystyle\frac{a_n+b_n}{2}-a_n=\frac{b_n-a_n}{2}
\end{cases}$$
です。
ここで、任意の$n\in\mathbb{N}$に対して、$a_n\in A$であり、かつ$b_n\in B$です。
従って、任意の$n\in\mathbb{N}$に対して、$a_n<b_n$($(A,B)$は切断だから)であるので、任意の$n\in\mathbb{N}$で、$\displaystyle\frac{b_n-a_n}{2}>0$です。
以上により、数列$\{a_n\}_{n\in\mathbb{N}}$は単調増加数列です。
さらに、$(A,B)$が切断であるので、任意の$a\in A$に対して$a<b$という$b\in B$が取れるのだから、上に有界です。
同様にして、
$$b_{n+1}=\begin{cases}
b_n \\
\displaystyle\frac{a_n+b_n}{2}
\end{cases}$$
であるから、
$$b_{n+1}-b_n=\begin{cases}
b_n-b_n=0 \\
\displaystyle\frac{a_n+b_n}{2}-b_n=\frac{a_n-b_n}{2}
\end{cases}$$
です。
上記と同じ理由で、任意の$n\in\mathbb{N}$で$\displaystyle\frac{a_n-b_n}{2}<0$です。
以上により、数列$\{b_n\}_{n\in\mathbb{N}}$は単調減少数列です。
さらに、$(A,B)$が切断であるので、任意の$b\in A$に対して$a<b$という$a\in B$が取れるのだから下に有界です。

(ステップ1-3)
ここで、
$$\lim_{n\to\infty}(b_n-a_n)=\lim_{n\to\infty}\frac{1}{2^n}(b-a)=0$$
である。(これを証明するためにアルキメデスの原理を使う！)
次で証明を与えます。
まずはアルキメデスの原理の証明を与えます。

アルキメデスの原理 $$(\forall a\in\mathbb{R}_{>0})(\forall b\in\mathbb{R}_{>0})(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ b<N_0a$$ ただし、$\mathbb{R}_{>0}=\{x\in\mathbb{R}\mid x>0\}$、すなわち正の実数の集合である。

少々余談なのだが、アルキメデスの原理は今まで何度か出現していたが証明を与えていませんでした。
また、これは解析学を語る上でよく出現する事実であるため、そういう意味で重要です。
また、アルキメデスの原理はワイエルシュトラスの上限公理から導かれます。

ワイエルシュトラスの上限公理(上限公理、有界性公理) $A\subset \mathbb{R}$、$A\neq\emptyset$、$A$は上に有界であるとする。このとき$A$の上限$\sup A$が存在する。つまり、上に有界かつ空でない$\mathbb{R}$の任意の部分集合は上限を持つ。

アルキメデスの原理の証明

背理法を用います。
仮に、アルキメデスの原理が成り立たないとします。
すなわち、
$$(\exists a\in\mathbb{R}_{>0})(\exists b\in\mathbb{R}{>0})\ {\rm s.t.}\ (\forall N_0\in\mathbb{N})\ {\rm s.t.}\ b\geq N_0a\dots(※)$$
が成り立ったとします。
すなわち、上記を満たすような正の実数$a$および$b$を見つけることができる、と仮定します。
このとき、$A=\{na\mid n\in\mathbb{N}\}$とおくと、$A\subset\mathbb{R}\neq\emptyset$が成り立ちます。
また、(※)により、$A$は上に有界であることがわかります（$b$が$A$の上界となっているため）。
従って、ワイエルシュトラスの上限公理の仮定を満たします。
ワイエルシュトラスの上限公理から、$A$の上限$S$が存在します。
$S$は$A$の上限であるため、

$(\forall x\in A)x\leq S$,
$(\forall \epsilon>0)(\exists x\in A)\ {\rm s.t.}\ x>S-\epsilon$

が成り立ちます。
すなわち、上記を満たすような$x\in A$を見つけることができます。
2.は任意の正の実数$\epsilon$で成り立つのだから、最初に見つけてきた$a$を用いて$\epsilon=\displaystyle \frac{a}{2}$としても成り立ちます。
従って、先程見つけた$x\in A$を用いて
$$S-\epsilon S+\epsilon>S$$
です。
従って、$y\in A$かつ$y>S$だが、これは$S$が$A$の上限であることに反します。
すなわち、上限$S$よりも大きな$A$の要素が見つかってしまったので、矛盾。

アルキメデスの原理の証明終わり

次に(ステップ1-2)で出現した
$$\lim_{n\to\infty}(b_n-a_n)=\lim_{n\to\infty}\frac{1}{2^n}(b-a)=0$$
を示します。

補題7. $$\lim_{n\to\infty}\left(\frac{1}{2}\right)^n(b-a)=0$$

補題7.の証明

示したいことは、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow \left|\left(\frac{1}{2}\right)^n(b-a)-0\right|<\epsilon)$$
です。
任意の自然数$n$に対して、$2^n>n$を満たします。
数学的帰納法により示します。
$n=1$のとき、$2^n=2$であるから、$2^n>n$が成り立ちます。
$n=k$のとき成り立ったとすると、$2^k>k$です。
$n=k+1$のとき、$2^{k+1}>k+1$であればOKです。
$k\geq1$であることに注意すれば、
$2^{k+1}=2\cdot 2^k>2k=k+k\geq k+1$
となり成立します。
従って、$\displaystyle\frac{1}{2^n}(b-a)<\frac{1}{n}\cdot (b-a)$が成り立ちます。
ゆえに、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow \left|\frac{1}{n}\cdot (b-a) -0\right|<\epsilon)\cdots①$$
が示されれば、
$\displaystyle\frac{1}{2^n}(b-a)<\frac{1}{n}\cdot (b-a)$が成り立つので、$\displaystyle\left|\left(\frac{1}{2}\right)^n(b-a)-0\right|<\epsilon$が成り立ち、$\displaystyle\left|\left(\frac{1}{2}\right)^n-0\right|<\frac{\epsilon}{b-a}$が成り立つので、証明が終わります。
(※ちなみに、$\epsilon$は任意の正の実数だったので、$\frac{\epsilon}{b-a}$も任意の正の実数である。)
すなわち、本質的には
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow \left|\frac{1}{n}-0\right|<\epsilon)$$
が示されれば、$\left(\displaystyle\lim_{n\to\infty}\frac{1}{n}=0\right)$を示したことになり、証明が終わります。
しかし、これはすでに証明しています(【解析学の基礎シリーズ】実数の連続性編その8)。
従って、①が成り立つ。

補題7.の証明終わり

では、(ステップ1-2)の証明に戻りましょう。
上記の話から
$$\lim_{n\to\infty}(b_n-a_n)=\lim_{n\to\infty}\frac{1}{2^n}(b-a)=0$$
が成り立ちました。

(ステップ2-1)
すると、今得られた区間の列$\{I_n\}_{n\in\mathbb{N}}$は区間縮小の原理の仮定を満たします。
従って、区間縮小の原理から、
$$\bigcap_{n\in\mathbb{N}}I_n=\{c\}$$
という実数$c$が存在します。
さて、$(A,B)$は実数の切断であったので、今見つけた$c$も$A$か$B$かいずれか一方の要素です。

(ステップ2-2)
今、$c\in A$だったとします。
このとき、$c$が$A$の最大値であり、かつ$B$には最小値がなければ良いです。
仮に、$c$が$A$の最大値でなかったとします(背理法！)。
ここで、最大値および最小値とは何だったかというと、

最大値、最小値 $A\subset \mathbb{R}$とする。このとき、$S\in\mathbb{R}$が

$(\forall x\in A)(x\leq S)$,
$S\in A$.

を満たすとき、$S$は$A$の最大値という。
また、このとき、$I\in\mathbb{R}$が

$(\forall x\in A)(x\geq I)$,
$I\in A$.

を満たすとき、$I$は$A$の最小値という。

でした。
今、$c$が$A$の最大値でないので、
$$(\exists x\in A)\ {\rm s.t.}\ x>cまたはc\not\in A$$
が成り立ちます。
今、$c\in A$であるため、$(\exists x\in A)\ {\rm s.t.}\ x>c$が成り立ちます。
すなわち、$x>c$を満たすような$x\in A$を見つけてくることができます。
このとき、$x\in A$はある正の実数$\epsilon_0$を用いて$x=c+\epsilon_0$と書けます。
区間縮小の原理から、$\displaystyle\lim_{n\to\infty}b_n=c$であるので、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |b_n-c)|<\epsilon)$$
が成り立つ。すなわち、上記を満たすような自然数$N$を見つけることができます。
ここで、$\epsilon>0$はすべての正の実数を表すため、先の見つけた正の実数$\epsilon_0$でも成り立ちます。
従って、先程見つけてきた$N$も用いて
$$\forall n\in\mathbb{N}\ n\geq N\Rightarrow |b_n-c|<\epsilon_0$$
が成り立ちます。
数列$\{b_n\}_{n\in\mathbb{N}}$は下に有界な単調減少数列だから、$c$は集合$\{b_n\mid n\in\mathbb{N}\}$の下限です。
従って、任意の$m\in\mathbb{N}$に対して、$c<b_m$なのだから、$n\geq N$を満たす自然数$n$についても$c<b_n$が成り立ちます。
ここで、$|b_n-c|<\epsilon_0$だったのだから、$-\epsilon_0<b_n-c<\epsilon_0$です。
ゆえに$b_n<c+\epsilon_0$です
従って、$c<b_n<c+\epsilon_0=x$を得ます。
ここで、$b_n\in B$であるから、$x\in B$であるはずだが、$x\in A$であるので矛盾です。
以上のことから、$c$は$A$の最大値です。
このとき、$B$には最小値が存在しません。
仮に$B$に最小数が合ったとすると、$c$は$\{b_n\mid n\in\mathbb{N}\}$の下限であるので、最小値が存在したらならば$c$であるから、$c\in B$です。
今、$c\in A$であるため、$c\in A\cap B$です。
しかし、これは$(A,B)$が切断であることに反します。

(ステップ2-3)
次に、$c\in B$のときを考えます。
先と同様です。
このとき、$A$には最大値がなく、かつ$B$には最小値があれば良いです。
仮に、$c$が$B$の最小値でなかったとしましょう(背理法！)。
$$(\exists x\in B)\ {\rm s.t.}\ x<cまたはc\not\in B$$
が成り立ちます。
今、$c\in B$であるため、$(\exists x\in B)\ {\rm s.t.}\ x<c$が成り立ちます。
すなわち、$x<c$を満たすような$x\in B$を見つけてくることができます。
このとき、$x\in B$はある正の実数$\epsilon_0$を用いて$x=c-\epsilon_0$と書けます。
区間縮小の原理から、$\displaystyle\lim_{n\to\infty}a_n=c$であるので、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |a_n-c)|<\epsilon)$$
が成り立ちます。
すなわち、上記を満たすような自然数$N$を見つけることができます。
ここで、$\epsilon>0$はすべての実数を表すため、先の見つけた正の実数$\epsilon_0$でも成り立ちます。
従って、先程見つけてきた$N$も用いて
$$\forall n\in\mathbb{N}\ n\geq N\Rightarrow |a_n-c|<\epsilon_0$$
が成り立ちます。
数列$\{a_n\}_{n\in\mathbb{N}}$は上に有界な単調増加数列だから、$c$は集合$\{a_n\mid n\in\mathbb{N}\}$の上限です。
従って、任意の$m\in\mathbb{N}$に対して、$a_m<c$なのだから、$n\geq N$を満たす自然数$n$についても$a_n<c$が成り立ちます。
ここで、$|a_n-c|<\epsilon_0$だったのだから、$-\epsilon_0<a_n-c<\epsilon_0$である。
ゆえに$a_n>c-\epsilon_0$です。
従って、$c-\epsilon_0=x<a_n<c$を得ます。
ここで、$a_n\in A$であるから、$x\in A$であるはずだが、$x\in B$であるので矛盾。
以上のことから、$c$は$B$の最小値です。
このとき、$A$には最大値が存在しません。
仮に$A$に最小数があったとすると、$c$は$\{a_n\mid n\in\mathbb{N}\}$の上限であるので、最大値が存在したらならば$c$であるから、$c\in A$です。
今、$c\in B$であるため、$c\in A\cap B$です。
しかし、これは$(A,B)$が切断であることに反します。
従ってデデキントの定理が成り立ちます。

証明終わり

実数の連続性との関係性

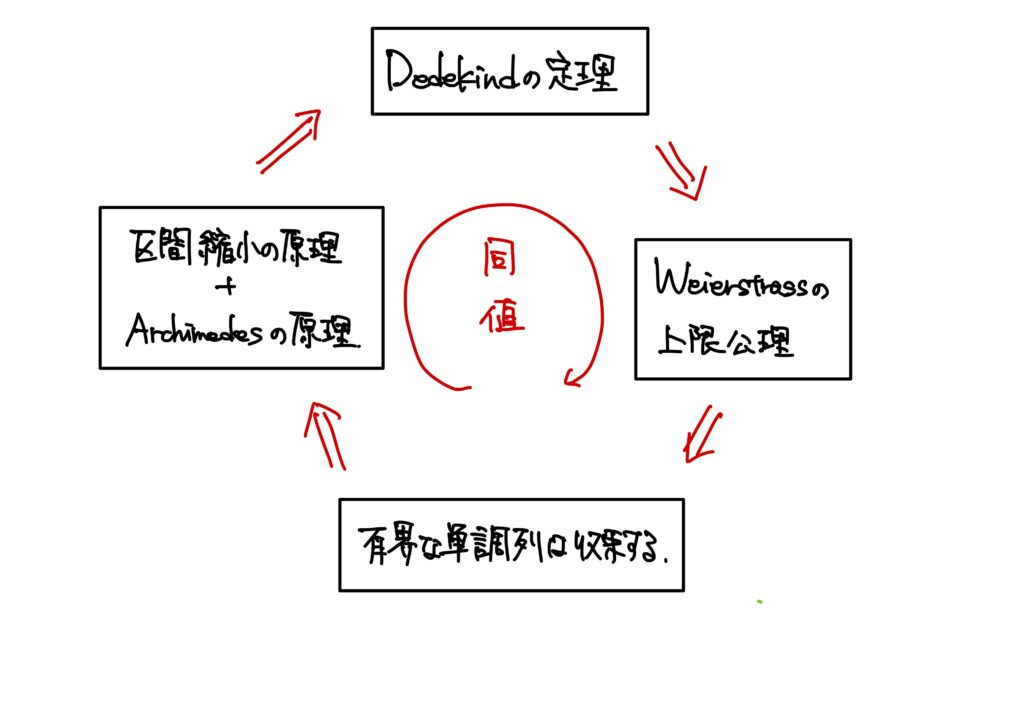
「区間縮小の原理+アルキメデスの原理$\Rightarrow$デデキントの定理」を示すことによって、
$${\rm デデキント}の定理\Rightarrow {\rm ワイエルシュトラス}の上限公理\Rightarrow「有界な単調列は収束する。」\\
\Rightarrow 区間縮小の原理+{\rm アルキメデス}の原理\Rightarrow {\rm デデキント}の定理$$
が証明されたことになるため、これら4つは全て同値である事が分かります。

結

今回は区間縮小法とアルキメデスの原理からデデキントの証明を与えました。
また、アルキメデスの原理の証明も与えました。

アルキメデスの原理は、解析学の中でも基本的な(簡単という意味ではない)事実であるため、ぜひ覚えてほしいところです。
区間縮小の原理は「だんだん小さくなっていく有界な閉区間が無限に続くとき、その共通部分は1点のみからなる集合だ。」と直感的に思える主張であるため、「実数の数直線上に”すき間”が無い」という直感に対応します。
したがって、そういう意味では実数の連続性と関連があります。

さらに、今回は

デデキントの定理
ワイエルシュトラスの上限公理
有界な単調列は収束する。
区間縮小の原理+アルキメデスの原理

がそれぞれ同値であることも間接的にではあるが示しました。
実は、実数の連続性と同値な命題はまだあります。

次回は「ボルツァーノ-ワイエルシュトラスの定理」です

乞うご期待！質問、コメントなどお待ちしております！

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34