本記事の内容
本記事は線型写像と行列の関係性について解説する記事です。
本記事を読むにあたり、写像について知っている必要があるため、以下の記事も合わせてご覧ください。
※シリーズ化しているため、一部の記事のリンクを掲載しています。
※注意※ 本記事は実行列と実ベクトルのみを扱います。
線型写像ってなんスか?
線型写像を一言で
線型写像を一言でいうと、
です。
「ありゃ?像ってなんだっけ?」というと、写像\(f:X\to Y\)および\(x\in X\)に対して\(f(x)\in Y\)のことです。
詳しくは【論理と集合シリーズ】写像編 その4を御覧ください。
線型写像をもっと端的に言うと、
「ナンジャソレ?」となるかもしれませんので、簡単な例を挙げます。
例えばどんなのッスか?
例1.\(f:\mathbb{R}\to\mathbb{R}\)を\(f(x)=2x\)で定めます。
このとき、
- 任意の\(a,b\in\mathbb{R}\)に対して\(f(a+b)=2(a+b)=2a+2b=f(a)+f(b)\)
- 任意の\(c\in\mathbb{R}\)および任意の\(a\in\mathbb{R}\)に対して\(f(ca)=2(ca)=c\cdot2a=cf(a)\)
が成り立ちます。
このとき\(f\)は線型写像であるといいます。
一方で、次の例を考えてみます。
例2.\(g:\mathbb{R}\to\mathbb{R}\)を\(g(x)=x^2\)で定めます。
このとき、
- 任意の\(a,b\in\mathbb{R}\)に対して\(f(a+b)=(a+b)^2=a^2+2ab+b^2\)となり、必ずしも\(f(a+b)\)と\(f(a)+f(b)\)は等しくありません。
- 任意の\(c\in\mathbb{R}\)および任意の\(a\in\mathbb{R}\)に対して\(f(ca)=(ca)^2=c^2a^2=c^2f(a)\)となり、必ずしも\(f(ca)\)と\(cf(a)\)は等しくありません。
この\(g\)は線型写像ではありません。
ベクトルの方がよりわかりやすいと思われますので、別の例を挙げます。
例3.\(h:\mathbb{R}^2\to\mathbb{R}^3\)を
$$
h\left(
\begin{array}{c}
x\\
y\\
\end{array}
\right)
=
\left(
\begin{array}{c}
x+y\\
2x\\
x-3y \\
\end{array}\right)
$$
で定めます。
このとき
- 任意の\(\displaystyle
\boldsymbol{a}=\left(
\begin{array}{c}
a_1\\ a_2\\
\end{array}
\right),\ \boldsymbol{b}=\left(
\begin{array}{c}
b_1\\ b_2\\
\end{array}
\right)\in\mathbb{R}^2\)に対して以下が成り立ちます。
\begin{eqnarray}
h(\boldsymbol{a}+\boldsymbol{b})&=&h\left(
\left(\begin{array}{c}a_1\\ a_2\\\end{array}\right)+\left(\begin{array}{c}b_1\\ b_2\\\end{array}\right)\right)\\
&=&h\left(\begin{array}{c}a_1+b_1\\ a_2+b_2\\\end{array}\right)\\
&=&
\left(
\begin{array}{c}a_1+b_1+a_2+b_2\\
2(a_1+b_1)\\
a_1+b_1-3(a_2+b_2)\\
\end{array}\right)\\
&=&
\left(\begin{array}{c}a_1+a_2\\ 2a_1\\a_1-3a_2 \end{array}\right)+\left(\begin{array}{c}b_1+b_2\\ 2b_1\\b_1-3b_2 \end{array}\right)\\
&=&h
\left(\begin{array}{c}a_1\\ a_2\end{array}\right)+h\left(\begin{array}{c}b_1\\ b_2\end{array}\right)=h(\boldsymbol{a})+h(\boldsymbol{b})
\end{eqnarray} - 任意の\(c\in\mathbb{R}\)および任意の\(\displaystyle\boldsymbol{a}=\left(\begin{array}{c}a_1\\ a_2\\\end{array}\right)\)に対して、以下が成り立ちます。
$$
h\left(c\left(\begin{array}{c}a_1\\ a_2\end{array}\right)\right)=h\left(\left(\begin{array}{c}ca_1\\ ca_2\end{array}\right)\right)=\left(\begin{array}{c}ca_1+ca_2\\ 2ca_1\\ ca_1-3ca_2\end{array}\right)=c\left(\begin{array}{c}ca_1+ca_2\\ 2ca_1\\ ca_1-3ca_2\end{array}\right)=ch\left(\left(\begin{array}{c}a_1\\ a_2\end{array}\right)\right)
$$
従って、\(h\)は線型写像です。
というわけで、線型写像とは何か、ということを明示します。
で、何スか?線型写像って?
で、線型写像は何か、ということをしっかり書くと以下です。
\(\mathbb{R}^n\)から\(\mathbb{R}^m\)への線型写像
写像\(f:\mathbb{R}^n\to\mathbb{R}^m\)が線型写像(linear mapping)であるとは、任意の\(\boldsymbol{a},\boldsymbol{b}\mathbb{R}^n\)および任意の\(c\in\mathbb{R}\)に対していかが成り立つときをいう。- \(f(\boldsymbol{a}+\boldsymbol{b})=f(\boldsymbol{a})+f(\boldsymbol{b})\) (和を保つ)
- \(f(c\boldsymbol{a})=cf(\boldsymbol{a})\) (スカラー倍を保つ)
ここで注意が2つほどあります。
- 注意1:「\(\mathbb{R}^n)から(\mathbb{R}^m\)への」という枕詞をつけたのは、線型写像は\(\mathbb{R}^n\)を一般化した線型空間で定められる概念だからです。
詳しくは線型空間の部分で解説します。 - 注意2:「保つ」という言葉はあまり聞き馴染みがないかと思いますが、演算について語る上では比較的よく出現します。
どういう意味か、ということをサラッというと、「定義域内で演算した要素を写像で対応させると、その行き先(対応している要素)での演算をした要素となっている」ということです。
つまり、厳密に言えば\(f(\boldsymbol{a}+\boldsymbol{b})=f(\boldsymbol{a})+f(\boldsymbol{b})\)の左辺の\(+\)と右辺の\(+\)は別物なのです。
すなわち左辺の\(+\)は\(\mathbb{R}^n\)での\(+\)なのであって、右辺の\(+\)は\(\mathbb{R}^m\)での\(+\)です。
故に\(\mathbb{R}^n\)での\(+\)を\(+_n\)と書き、\(\mathbb{R}^m\)での\(+\)を\(+_m\)と書いて\(f(\boldsymbol{a}+_n\boldsymbol{b})=f(\boldsymbol{a})+_mf(\boldsymbol{b})\)と書いた方が厳密です。
スカラー倍でも同じです。
線型写像は合成しても線型写像です
1つ自然にわかる事実を証明します。
以下に主張とその証明を書きますが、ぜひ一度ご自身で証明してみてください!
命題3.(線型写像の合成写像も線型写像)
\(m,n.l\in\mathbb{N}\)、\(f:\mathbb{R}^n\to\mathbb{R}^m\)および、\(g:\mathbb{R}^m\to\mathbb{R}^l\)が線型写像だとする。このとき、\(f\)と\(g\)の合成写像\(g\circ f:\mathbb{R}^n\to\mathbb{R}^l\)も線型写像である。命題3.の証明
\(m,n,l\in\mathbb{N}\)、\(f:\mathbb{R}^n\to\mathbb{R}^m\)および、\(g:\mathbb{R}^m\to\mathbb{R}^l\)が線型写像だとします。
このとき、示したいのは、任意の\(\boldsymbol{a},\boldsymbol{b}\in\mathbb{R}^n\)および\(c\in\mathbb{R}\)に対して、
- \((g\circ f)(\boldsymbol{a}+\boldsymbol{b})=(g\circ f)(\boldsymbol{a})+(g\circ f)(\boldsymbol{b})\)
- \((g\circ f)(c\boldsymbol{a})=c(g\circ f)(\boldsymbol{a})\)
です。
任意の\(\boldsymbol{a},\boldsymbol{b}\in\mathbb{R}^n\)に対して、\(f\)が線型写像であるから、
$$
(g\circ f)(\boldsymbol{a}+\boldsymbol{b})=g\left( f(\boldsymbol{a}+\boldsymbol{b})\right)=g\left( f(\boldsymbol{a})+f(\boldsymbol{b})\right)
$$
です。
また、\(g\)が線型写像であることから、
$$
g\left( f(\boldsymbol{a})+f(\boldsymbol{b})\right)=g\left( f(\boldsymbol{a})\right)+g\left( f(b)\right)=(g\circ f)(\boldsymbol{a})+(g\circ f)(\boldsymbol{b})
$$
です。
任意の\(\boldsymbol{a}\)および\(c\in\mathbb{R}\)に対して、\(f\)が線型写像であるから、
$$
(g\circ f)(c\boldsymbol{a})=g\left( f(c\boldsymbol{a})\right)=g\left( cf(\boldsymbol{a})\right)
$$
です。
また、\(g\)が線型写像であることから、
$$
g\left( cf(\boldsymbol{a})\right)=cg\left( f(\boldsymbol{a})\right)=c(g\circ f)(\boldsymbol{a})
$$
です。
命題3.の証明終わり
線型写像の行列表現
いきなりネタバラシなのですが、実は線型写像は行列によって書き表すことができ、逆に行列は線型写像を定めます。
そういう意味で両者を同一視することができます。
本節ではそれを解説します。
標準基底
まずは標準基底について解説します。
\(\mathbb{R}^n\)の標準基底
\(n\in\mathbb{N}\)とし、\(\mathbb{R}^n\)のベクトルを列ベクトルで表すことにして、以下のベクトルを考える。 $$ \boldsymbol{e}_1= \left( \begin{array}{c} 1\\ 0\\ \vdots \\ \vdots \\ 0 \end{array} \right),\quad \boldsymbol{e}_2= \left( \begin{array}{c} 0\\ 1\\ 0 \\ \vdots \\ 0 \end{array} \right),\cdots, \boldsymbol{e}_j= \left( \begin{array}{c} 0\\ \vdots\\ 1 \\ \vdots \\ 0 \end{array} \right)(\leftarrow j番目),\cdots, \boldsymbol{e}_n= \left( \begin{array}{c} 0\\ \vdots\\ \vdots \\ 0 \\ 1 \end{array} \right) $$ すなわち、各\(j=1,2,\cdots,n\)に対して、\(j\)番目の成分が\(1\)で、他の成分がすべて\(0\)であるようなベクトルが\(\boldsymbol{e}_j\)である。 このとき、\(n\)個のベクトルの組 $$ \boldsymbol{e}_1,\ \boldsymbol{e}_2,\cdots,\boldsymbol{e}_n $$ を\(\mathbb{R}^n\)の標準基底(standard basis, canonical basis)と呼ぶ。さらっと基底について述べておきます。
基底、特に標準基底はある種の座標軸のような役割を持っています。
例えば、2次元の場合を考えてみましょう。
2次元の場合の標準基底は
$$
\boldsymbol{e}_1=\left(
\begin{array}{c}
1\\
0
\end{array}
\right),\quad
\boldsymbol{e}_2=\left(
\begin{array}{c}
0\\
1
\end{array}
\right)
$$
です。
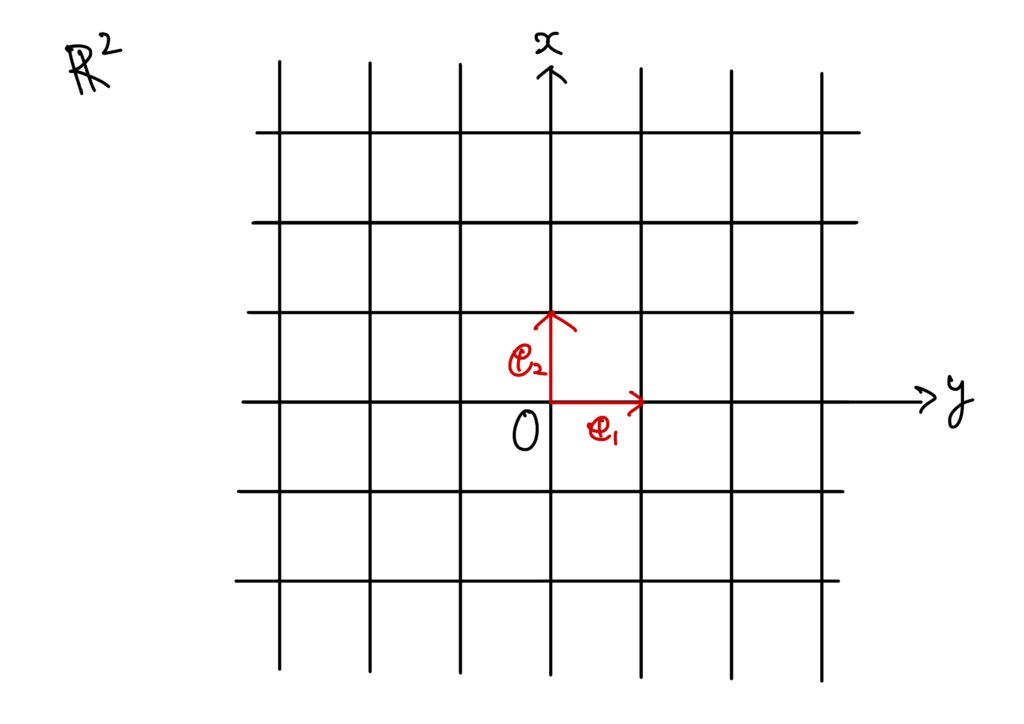
このとき、平面\(\mathbb{R}^2\)の任意の点は\(\boldsymbol{e}_1,\boldsymbol{e}_2\)を用いて一意的に表現することができます。
例えば、\((2,3)\)という点は
$$
\left(
\begin{array}{c}
2\\
3
\end{array}\right)=
2\left(
\begin{array}{c}
1\\
0
\end{array}
\right)+3\left(
\begin{array}{c}
0\\
1
\end{array}
\right)=2\boldsymbol{e}_1+3\boldsymbol{e}_2
$$
です。
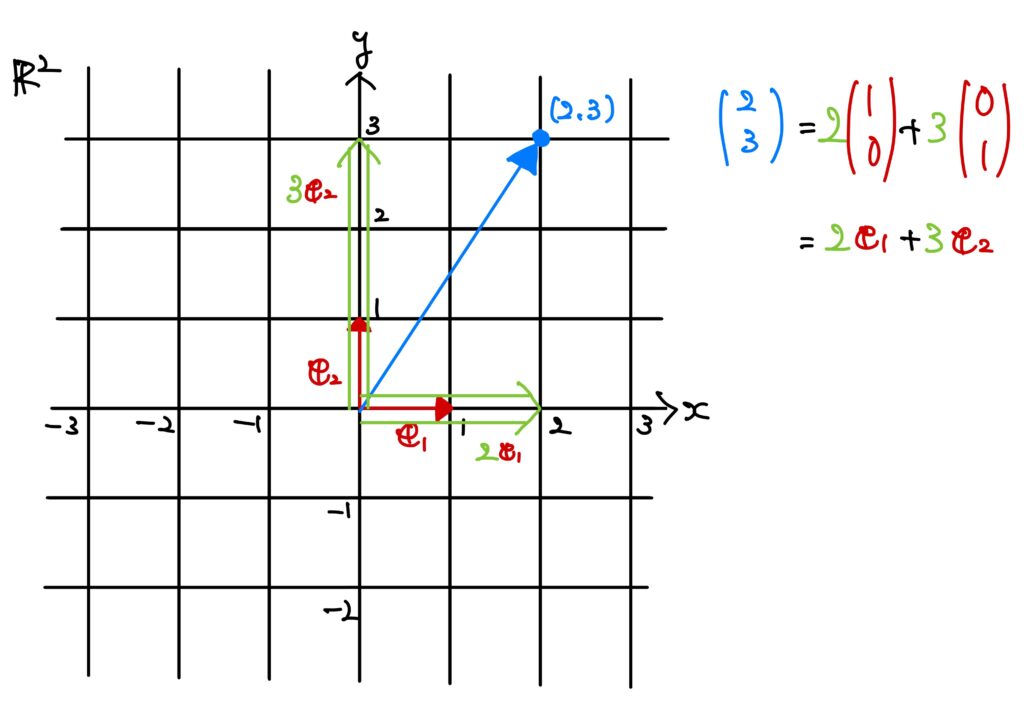
そういう意味で座標軸的な役割を担っています。
そのため、この標準基底に注目し、線型写像によって標準基底がどの要素と対応するのか、ということ着目すれば線型写像と行列の関係が分かります。
標準基底に着目してみる
では、「線型写像は行列で表現できまっせ」ということを見ていきましょう。
線型写像\(f:\mathbb{R}^n\to\mathbb{R}^m\)が与えられたとし、\(\boldsymbol{e}_1,\ \boldsymbol{e}_2,\cdots,\boldsymbol{e}_n\)が\(\mathbb{R}^n\)の標準基底だとします。
ここで、注意なのが、\(\boldsymbol{e}_1,\ \boldsymbol{e}_2,\cdots,\boldsymbol{e}_n\)は\(0\)か\(1\)が縦に\(n\)個並んだベクトルです。
さてこのとき、\(\mathbb{R}^n\)の標準基底の像\(f(\boldsymbol{e}_1),f(\ \boldsymbol{e}_2),\cdots,f(\boldsymbol{e}_n)\)を考えてみましょう。
これら\)が\(\mathbb{R}^n\)の標準基底だとします。
このとき、\(\mathbb{R}^n\)の標準基底の像\(f(\boldsymbol{e}_1),f(\ \boldsymbol{e}_2),\cdots,f(\boldsymbol{e}_n)\)は\(\mathbb{R}^m\)の要素ですから、それぞれが\(\mathbb{R}^m\)のベクトルです。
従って、\(f(\boldsymbol{e}_1),f(\ \boldsymbol{e}_2),\cdots,f(\boldsymbol{e}_n)\)を以下のように書いてみます。
$$
f(\boldsymbol{e}_1)=
\left(
\begin{array}{c}
a_{11}\\
a_{21}\\
\vdots \\
\vdots \\
a_{m1}
\end{array}
\right),\quad
f(\boldsymbol{e}_2)=
\left(
\begin{array}{c}
a_{12}\\
a_{22}\\
\vdots \\
\vdots \\
a_{m2}
\end{array}
\right),\cdots,
f(\boldsymbol{e}_j)=
\left(
\begin{array}{c}
a_{1j}\\
a_{2j}\\
\vdots \\
\vdots \\
a_{mj}
\end{array}
\right),\cdots,
f(\boldsymbol{e}_n)=
\left(
\begin{array}{c}
a_{1n}\\
a_{2n}\\
\vdots \\
\vdots \\
a_{mn}
\end{array}
\right)
$$
ここで、\(\mathbb{R}^m\)の標準基底を\(\boldsymbol{e}^\prime_1,\ \boldsymbol{e}^\prime_2,\cdots,\boldsymbol{e}^\prime_m\)と書いたとしましょう。
すなわち、
$$
\boldsymbol{e}^\prime_1=
\left(
\begin{array}{c}
1\\
0\\
\vdots \\
\vdots \\
0
\end{array}
\right),\quad
\boldsymbol{e}^\prime_2=
\left(
\begin{array}{c}
0\\
1\\
0 \\
\vdots \\
0
\end{array}
\right),\cdots,
\boldsymbol{e}^\prime_k=
\left(
\begin{array}{c}
0\\
\vdots\\
1 \\
\vdots \\
0
\end{array}
\right)(\leftarrow k番目),\cdots,
\boldsymbol{e}^\prime_m=
\left(
\begin{array}{c}
0\\
\vdots\\
\vdots \\
0 \\
1
\end{array}
\right)
$$
ここで注意なのが、\(\boldsymbol{e}^\prime_1,\ \boldsymbol{e}^\prime_2,\cdots,\boldsymbol{e}^\prime_m\)は\(0\)か\(1\)が縦に\(m\)個並んだベクトルです。
先程の\(f(\boldsymbol{e}_1),f(\ \boldsymbol{e}_2),\cdots,f(\boldsymbol{e}_n)\)は\(\mathbb{R}^m\)の要素だったわけですから、これらを\(\boldsymbol{e}^\prime_1,\ \boldsymbol{e}^\prime_2,\cdots,\boldsymbol{e}^\prime_m\)をつかって表現してみます。
ここでは\(f(\boldsymbol{e}_j)\)に注目してみましょう。
すると、
\begin{eqnarray}
f(\boldsymbol{e}_j)&=&
\left(
\begin{array}{c}
a_{1j}\\
a_{2j}\\
\vdots \\
\vdots \\
a_{mj}
\end{array}
\right)=
\left(
\begin{array}{c}
a_{1j}\\
0\\
\vdots \\
\vdots \\
0
\end{array}
\right)+
\left(
\begin{array}{c}
0\\
a_{2j}\\
0 \\
\vdots \\
0
\end{array}
\right)+\dots+
\left(
\begin{array}{c}
0\\
\vdots\\
a_{kj}\\
\vdots \\
0
\end{array}
\right)(\leftarrow k番目)+\dots+
\left(
\begin{array}{c}
0\\
\vdots\\
\vdots \\
0 \\
a_{mj}
\end{array}
\right)\\
&=&
a_{1j}\left(
\begin{array}{c}
1\\
0\\
\vdots \\
\vdots \\
0
\end{array}
\right)+a_{2j}
\left(
\begin{array}{c}
0\\
1\\
0 \\
\vdots \\
0
\end{array}
\right)+\dots+a_{kj}
\left(
\begin{array}{c}
0\\
\vdots\\
1\\
\vdots \\
0
\end{array}
\right)+\dots+a_{mj}
\left(
\begin{array}{c}
0\\
\vdots\\
\vdots \\
0 \\
1
\end{array}
\right)\\
&=&
a_{1j}\boldsymbol{e}^\prime_1+a_{2j}\boldsymbol{e}^\prime_2+\dots+a_{kj}\boldsymbol{e}^\prime_k+\dots+a_{mj}\boldsymbol{e}^\prime_m\\
&=&
\sum_{i=1}^ma_{ij}\boldsymbol{e}_i^\prime
\end{eqnarray}
です。
まとめれば、
ということです。
次に、\(f(\boldsymbol{e}_1),f(\ \boldsymbol{e}_2),\cdots,f(\boldsymbol{e}_n)\)を列ベクトルとする\((m,n)\)行列\(A\)を考えます。
すなわち、
$$
A=
\begin{pmatrix}
a_{11}&a_{12}&\cdots &a_{1n}\\
a_{21}&a_{22}&\cdots &a_{2n}\\
\vdots&\vdots& \ddots&\vdots\\
a_{m1}&a_{m2}&\cdots &a_{mn}\\
\end{pmatrix}=\left(f(\boldsymbol{e}_1)\ f(\ \boldsymbol{e}_2)\cdots f(\boldsymbol{e}_n) \right)
$$
となります。
つまり、線型写像から行列が定まったことになります。
これをまとめると、
ということです。
線型写像は行列で表現できる
ここまでは、\(f:\mathbb{R}^n\to\mathbb{R}^m\)の標準基底という特別なベクトルについて考えました。
これからは標準基底だけでなく一般の\(\boldsymbol{x}\in\mathbb{R}^n\)について考えてみましょう。
任意の\(x\in\mathbb{R}^n\)を
$$
\boldsymbol{x}=\left(
\begin{array}{c}
x_1\\
x_2\\
\vdots \\
x_n
\end{array}
\right)
$$
と書いたとしましょう。
この\(\boldsymbol{x}\in\mathbb{R}^n\)は\(\mathbb{R}^n\)の標準基底\(\boldsymbol{e}_1,\ \boldsymbol{e}_2,\cdots,\boldsymbol{e}_n\)を用いると、次のように書くことができます。
\begin{eqnarray}
\boldsymbol{x}&=&
\left(
\begin{array}{c}
x_1\\
x_2\\
\vdots\\
\vdots \\
\vdots \\
\vdots\\
x_n
\end{array}
\right)=
\left(
\begin{array}{c}
x_1\\
0\\
0\\
\vdots \\
\vdots \\
\vdots\\
0
\end{array}
\right)+
\left(
\begin{array}{c}
0\\
x_2\\
0\\
\vdots \\
\vdots \\
\vdots\\
0
\end{array}
\right)+\dots+
\left(
\begin{array}{c}
0\\
\vdots\\
0\\
x_j \\
0 \\
\vdots\\
0
\end{array}
\right)(\leftarrow j番目)+\dots+
\left(
\begin{array}{c}
0\\
\vdots\\
\vdots\\
\vdots \\
0 \\
0\\
x_n
\end{array}
\right)\\
&=&
x_1\left(
\begin{array}{c}
1\\
0\\
0\\
\vdots \\
\vdots \\
\vdots\\
0
\end{array}
\right)+
x_2\left(
\begin{array}{c}
0\\
1\\
0\\
\vdots \\
\vdots \\
\vdots\\
0
\end{array}
\right)+\dots+
x_j\left(
\begin{array}{c}
0\\
\vdots\\
0\\
1 \\
0 \\
\vdots\\
0
\end{array}
\right)(\leftarrow j番目)+\dots+
x_n\left(
\begin{array}{c}
0\\
\vdots\\
\vdots\\
\vdots \\
0 \\
0\\
1
\end{array}
\right)\\
&=&
x_1\boldsymbol{e}_1+x_2\boldsymbol{e}_2+\dots+x_j\boldsymbol{e}_j+\dots+x_n\boldsymbol{e}_n
\end{eqnarray}
さて、線型写像\(f:\mathbb{R}^n\to\mathbb{R}^m\)による\(x\in\mathbb{R}^n\)の像を考えてみましょう。
線型写像とは何だったかということを再掲しておきます。
\(\mathbb{R}^n\)から\(\mathbb{R}^m\)への線型写像(再掲)
写像\(f:\mathbb{R}^n\to\mathbb{R}^m\)が線型写像(linear mapping)であるとは、任意の\(\boldsymbol{a},\boldsymbol{b}\mathbb{R}^n\)および任意の\(c\in\mathbb{R}\)に対していかが成り立つときをいう。- \(f(\boldsymbol{a}+\boldsymbol{b})=f(\boldsymbol{a})+f(\boldsymbol{b})\) (和を保つ)
- \(f(c\boldsymbol{a})=cf(\boldsymbol{a})\) (スカラー倍を保つ)
線型写像の条件1.および2.を繰り返し使うことによって、
\begin{eqnarray}
f(\boldsymbol{x})&=&f\left(x_1\boldsymbol{e}_1+x_2\boldsymbol{e}_2+\dots+x_j\boldsymbol{e}_j+\dots+x_n\boldsymbol{e}_n\right)\\
&=&
f\left(x_1\boldsymbol{e}_1\right)+f\left(x_2\boldsymbol{e}_2\right)+\dots+f\left(x_j\boldsymbol{e}_j\right)+\dots+f\left(x_n\boldsymbol{e}_n\right)\\
&=&
x_1f\left(\boldsymbol{e}_1\right)+x_2f\left(\boldsymbol{e}_2\right)+\dots+x_jf\left(\boldsymbol{e}_j\right)+\dots+x_nf\left(\boldsymbol{e}_n\right)\\
\end{eqnarray}
です。
ここで、
$$
f(\boldsymbol{e}_1)=
\left(
\begin{array}{c}
a_{11}\\
a_{21}\\
\vdots \\
\vdots \\
a_{m1}
\end{array}
\right),\quad
f(\boldsymbol{e}_2)=
\left(
\begin{array}{c}
a_{12}\\
a_{22}\\
\vdots \\
\vdots \\
a_{m2}
\end{array}
\right),\cdots,
f(\boldsymbol{e}_j)=
\left(
\begin{array}{c}
a_{1j}\\
a_{2j}\\
\vdots \\
\vdots \\
a_{mj}
\end{array}
\right),\cdots,
f(\boldsymbol{e}_n)=
\left(
\begin{array}{c}
a_{1n}\\
a_{2n}\\
\vdots \\
\vdots \\
a_{mn}
\end{array}
\right)
$$
と書いたことを思い出すと、
\begin{eqnarray}
&&x_1f\left(\boldsymbol{e}_1\right)+x_2f\left(\boldsymbol{e}_2\right)+\dots+x_jf\left(\boldsymbol{e}_j\right)+\dots+x_nf\left(\boldsymbol{e}_n\right)\\
&=&
x_1\left(
\begin{array}{c}
a_{11}\\
a_{21}\\
\vdots \\
\vdots \\
a_{m1}
\end{array}
\right)+
x_2
\left(
\begin{array}{c}
a_{12}\\
a_{22}\\
\vdots \\
\vdots \\
a_{m2}
\end{array}
\right)+\cdots+
x_j
\left(
\begin{array}{c}
a_{1j}\\
a_{2j}\\
\vdots \\
\vdots \\
a_{mj}
\end{array}
\right)+\cdots+
x_n
\left(
\begin{array}{c}
a_{1n}\\
a_{2n}\\
\vdots \\
\vdots \\
a_{mn}
\end{array}
\right)
\\
&=&
\left(
\begin{array}{c}
x_1a_{11}+x_2a_{12}+\dots+x_ja_{1j}+\dots+x_na_{1n}\\
x_1a_{21}+x_2a_{22}+\dots+x_ja_{2j}+\dots+x_na_{2n}\\
\vdots \\
\vdots \\
x_1a_{m1}+x_2a_{m2}+\dots+x_ja_{mj}+\dots+x_na_{mn}
\end{array}
\right)
\end{eqnarray}
ここで「お?もしや?」と思った方、鋭いです。
「もしかして?」と思った方のその「もしかして」は正解です。
最後のベクトルは、行列とベクトルの積に書き直すことができます。
つまり、
\begin{eqnarray}
\left(
\begin{array}{c}
x_1a_{11}+x_2a_{12}+\dots+x_ja_{1j}+\dots+x_na_{1n}\\
x_1a_{21}+x_2a_{22}+\dots+x_ja_{2j}+\dots+x_na_{2n}\\
\vdots \\
\vdots \\
x_1a_{m1}+x_2a_{m2}+\dots+x_ja_{mj}+\dots+x_na_{mn}
\end{array}
\right)=
\begin{pmatrix}
a_{11}&a_{12}&\cdots &a_{1n}\\
a_{21}&a_{22}&\cdots &a_{2n}\\
\vdots&\vdots& \ddots&\vdots\\
a_{m1}&a_{m2}&\cdots &a_{mn}\\
\end{pmatrix}
\left(
\begin{array}{c}
x_1\\
x_2\\
\vdots \\
x_n
\end{array}
\right)
\end{eqnarray}
です。
「え?本当に?」と思った方はぜひ計算してみてください。
「嘘だr…ホントだ…」となると思います。
ここで、
$$
A=
\begin{pmatrix}
a_{11}&a_{12}&\cdots &a_{1n}\\
a_{21}&a_{22}&\cdots &a_{2n}\\
\vdots&\vdots& \ddots&\vdots\\
a_{m1}&a_{m2}&\cdots &a_{mn}\\
\end{pmatrix}
$$
と書いたとすると、今での話は
$$f(\boldsymbol{x})=A\boldsymbol{x}$$
ということです。
これはまさに、「線型写像は行列で表現できる」ということを指しています。
大事なことなので、この節のまとめとして明記しておきます。
行列は線型写像で表現できる
今までの話の流れとしては線型写像から行列を導き出そう、という流れでした。
今度はその逆、行列から線型写像を導こうという話です。
そもそものお話
まずは、行列とベクトルの積のそもそもの話をします。
$$
A=
\begin{pmatrix}
a_{11}&a_{12}&\cdots &a_{1n}\\
a_{21}&a_{22}&\cdots &a_{2n}\\
\vdots&\vdots& \ddots&\vdots\\
a_{m1}&a_{m2}&\cdots &a_{mn}\\
\end{pmatrix},\quad
\boldsymbol{x}=
\left(
\begin{array}{c}
x_1\\
x_2\\
\vdots \\
x_n
\end{array}
\right)
$$
としたとき、\(A\)は\((m,n)\)型の行列、\(\boldsymbol{x}\)は\(n\)次のベクトル、すなわち\((n,1)\)型の行列ですので\(A\)と\(\boldsymbol{x}\)の積\(A\boldsymbol{x}\)を考えることができます。
そこで\(A\boldsymbol{x}\)を計算してみます。
すると、
\begin{eqnarray}
A\boldsymbol{x}&=&
\begin{pmatrix}
a_{11}&a_{12}&\cdots &a_{1n}\\
a_{21}&a_{22}&\cdots &a_{2n}\\
\vdots&\vdots& \ddots&\vdots\\
a_{m1}&a_{m2}&\cdots &a_{mn}\\
\end{pmatrix}
\left(
\begin{array}{c}
x_1\\
x_2\\
\vdots \\
x_n
\end{array}
\right)\\
&=&
\left(
\begin{array}{c}
x_1a_{11}+x_2a_{12}+\dots+x_ja_{1j}+\dots+x_na_{1n}\\
x_1a_{21}+x_2a_{22}+\dots+x_ja_{2j}+\dots+x_na_{2n}\\
\vdots \\
\vdots \\
x_1a_{m1}+x_2a_{m2}+\dots+x_ja_{mj}+\dots+x_na_{mn}
\end{array}
\right)\in\mathbb{R}^m
\end{eqnarray}
です。
これを写像の視点からみてみます。
すると、
ということです。
これはまさに写像です。
すなわち、行列というのは行列とベクトルの積を規則とすることで、そもそも\(\mathbb{R}^n\)から\(\mathbb{R}^m\)への写像なのです。
ということは、行列は写像なのですから、この写像が線型写像だということが分かればゴールです。
行列が与える写像は線型写像だ
では、行列が与える写像が線型写像だということ示します。
任意の\((m,n)\)型の行列を\(A=(a_{ij})\)が与えられたとき、写像\(f_A:\mathbb{R}^n\to\mathbb{R}^m\)を
$$
\boldsymbol{x}=
\left(
\begin{array}{c}
x_1\\
x_2\\
\vdots \\
x_n
\end{array}
\right)
$$
に対して、
$$
f_A(\boldsymbol{x})=A\boldsymbol{x}
$$
により定めます。
このとき、\(f_A\)が線型写像だ、ということを示したいわけです。
要するに、以下が成り立てば良いわけです。
任意の\(\boldsymbol{x},\boldsymbol{y}\in\mathbb{R}^n\)と任意の\(k\in\mathbb{R}\)に対して、
- \(f_A(\boldsymbol{x}+\boldsymbol{y})=f_A(\boldsymbol{x})+f_A(\boldsymbol{y})\),
- \(f_A(k\boldsymbol{x})=kf_A(\boldsymbol{x})\)
が成り立てばOKです。
まずは1.を示します。
1.を示すにあたって、行列の積の分配則を使います。
「なんだったっけ?」というと、以下でした。
定理.(分配則)
\(m,n,r\in\mathbb{N}\)、\(k,h\in\mathbb{C}\)とする。このとき、3つの行列\(C\)に対して、以下が成り立つ。- \(A\)が\((m,n)\)型、\(B\)及び\(C\)が\((n,r)\)型のとき、\(A(B+C)=AB+AC\)
- \(A\)と\(B\)が\((m,n)\)型、\(C\)が\((n,r)\)型のとき、\((A+B)C=AC+BC\)
- \(A\)および\(B\)が共に\((m,n)\)型のとき、\(k(A+B)=kA+kB\)
- \(A\)および\(B\)が共に\((m,n)\)型のとき、\((k+h)A=kA+hA\)
この定理の証明は【線型代数学の基礎シリーズ】行列編 その2を御覧ください。
今、定理.(分配則)の1.において\(r=1\)の場合を使います。
すると、
$$
f_A(\boldsymbol{x}+\boldsymbol{y})=A(\boldsymbol{x}+\boldsymbol{y})=A\boldsymbol{x}+A\boldsymbol{y}=f_A(\boldsymbol{x})+f_A(\boldsymbol{y})
$$
です。
次に2.です。
2.を示すにあたって、スカラー倍の性質を使います。
「なんだったっけ?」というと、以下でした。
定理.(スカラー倍の性質)
\(k,h\in\mathbb{C}\)、\(m,n,r\in\mathbb{N}\)とする。\((m,n)\)型行列\(A\)と\((n,r)\)型行列\(B\)と\(k,h\)に対して次が成り立つ。- \((kh)A=k(hA)\)
- \(k(AB)=(kA)B=A(kB)\)
- \(0A=O_{mn}\quad\)
- \(1A=A\)
この定理の証明は【線型代数学の基礎シリーズ】行列編 その2を御覧ください。
今、定理.(スカラー倍の性質)の2.において\(r=1\)の場合を使います。
すると、
$$
f_A(k\boldsymbol{x})=A(k\boldsymbol{x})=k\left(A\boldsymbol{x}\right)=kf_A(\boldsymbol{x})
$$
となるので、\(f_A\)は線型写像です。
この章のまとめ
要するに、この章では以下のことを示したことになります。
定理.(線型写像と行列との関係)
\(m,n\in\mathbb{N}\)、\(\mathbb{R}^n\)および\(\mathbb{R}^m\)の標準基底をそれぞれ\(\boldsymbol{e}_1,\dots,\boldsymbol{e}_n\)および\(\boldsymbol{e}_1,\dots,\boldsymbol{e}_n\)とする。このとき、任意の線型写像\(f:\mathbb{R}^n\to\mathbb{R}^m\)に対して、 $$f(\boldsymbol{e}_j)=\sum_{i=1}^ma_{ij}\boldsymbol{e}_i^\prime\quad (j\in\mathbb{N},\ 1\leq j\leq n)$$ によって\((m,n)\)型の行列 $$ A=\left(a_{ij}\right) $$ が定まり、任意の\(\boldsymbol{x}\in\mathbb{R}^n\)に対して\(f(\boldsymbol{x})=A\boldsymbol{x}\)が成り立つ。逆に、任意の\((m,n)\)型行列\(A\)が与えられたとき、 $$ f_A(\boldsymbol{x})=A\boldsymbol{x}\quad (\boldsymbol{x}\in\mathbb{R}^n) $$ によって線型写像\(f_A:\mathbb{R}^n\to\mathbb{R}^m\)が定まる。
この対応によって、線型写像\(f:\mathbb{R}^n\to\mathbb{R}^m\)と\((m,n)\)型行列\(A\)は一対一対応する。
結
今回は、\(\mathbb{R}^n\)から\(\mathbb{R}^m\)への線型写像は何か、ということと線型写像は行列で表現でき、逆に行列は線型写像であるということから線型写像と行列は同一視できるということを解説しました。
この説明にあたり、標準基底(座標軸のようなもの)に着目することで見通しが良くなるのでした。
今回の話は「行列ってなんとなく分かったけど結局何者?」という問に対して「線型写像です」と答える記事ということもできるでしょう。
次回は行列式の話をするために必要な「置換、互換、対称群(サラッと)、巡回置換、置換の符号」について解説します。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする