本記事の内容
本記事は中間値の定理の証明を与える記事です。
本記事を読むに当たり関数の連続性と区間縮小法を知っている必要があるため、その際は以下の記事を参照してください。
では、まずは中間値の定理のイメージを復習しましょう。
中間値の定理のイメージの復習
中間値の定理はどういうイメージだったかというと、
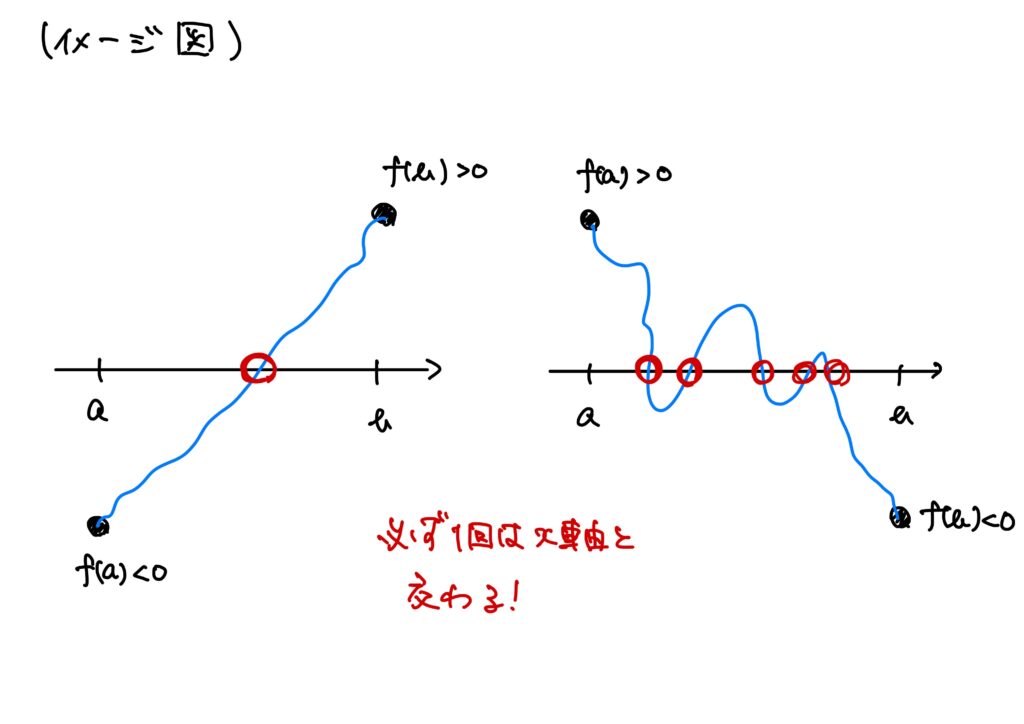
ということでした。
詳しくは【解析学の基礎シリーズ】関数の極限編 その13を参照してください。
実は、中間値の定理の主張はもう少し広いです。
「どういうことか?」というと、「\(x\)軸と少なくとも1回は交わる。」という部分の主張がもう少し広いです。
要は、\(x\)軸、すなわち\(y=0\)と交わるということを「\(y=D\)と少なくとも1回は交わる。」という主張に直すことができます。
つまりは上下(\(y\)軸方向)に平行移動したということです。
図とともに説明します。
とどのつまり、こういうことです。
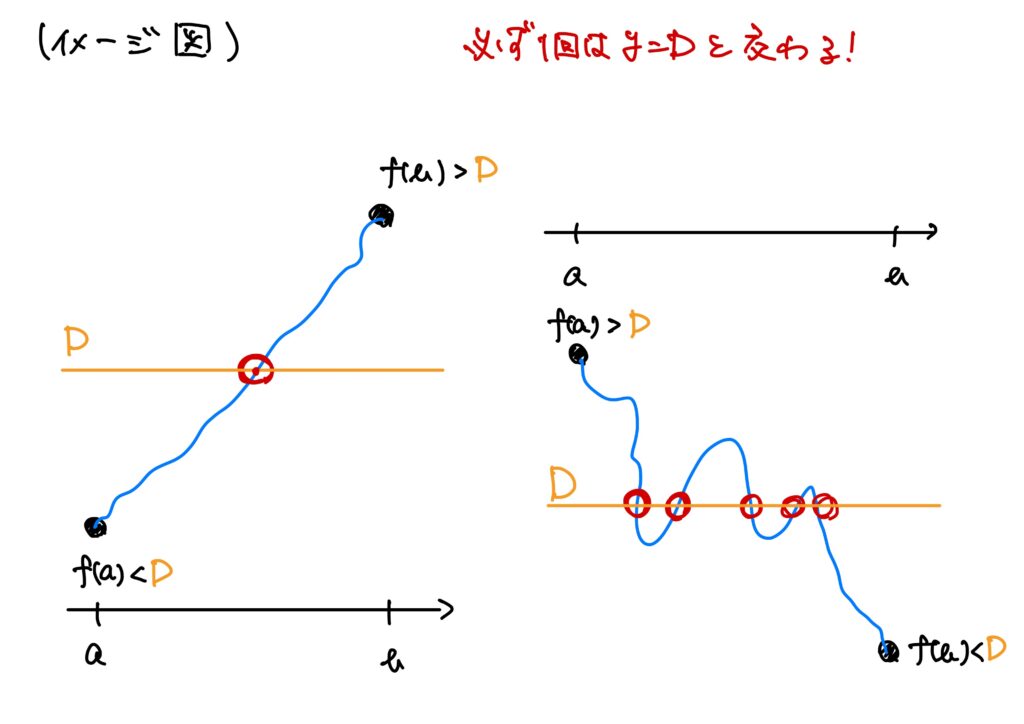
まさに、前回述べた中間値の定理を上下に平行移動した主張になっています。
前回述べたイメージは\(D=0\)の場合だった、というわけです。
今回は、\(y=D\)の場合を証明していきます。
では、中間値の定理とは何か、ということを明示します。
中間値の定理の明示

次にどういう発想で証明するかを説明します。
証明をするための発想
筆者は最初にこの定理を知ったとき、「当たり前じゃね?」と思いました。
「そりゃあ連続なら交わるでしょうよ」と思いました。
また同時に「どうすんだよ」とも思いました。
しかし、図を描いてみて「この主張は直感的には成り立つよね。ということは、この主張は\(f(x)=D\)という方程式の解\(x\)を求めろってことじゃないか?」
と思ったわけです。
示すことは\(f(d)=D\)となるような\(d\in(a,b)\)の存在です。
つまり、どのように\(d\)を見つけるのか、というアルゴリズムを提示することで証明が完了します。
ここで、「\(c\in[a,b]\)を任意に取ってきて、\(f(c)<D\)だったらば、\(f(c)\)が\(D\)に近づくように\(c+\epsilon\)(ちょっとずらして\(D\)に近づける、という意味)の値を考えて、\(f(c)>D\)だったらば\(f(c)\)が\(D\)に近づくように\(c-\epsilon\)(ちょっとずらして\(D\)に近づける、という意味)の値を考える。という操作を繰り返していけば\(d\)が求まるんじゃないか?」と思ったわけです。
(コンピュータで方程式を解くときはこのようにして解くんじゃないかな、なんて思ったりしてます。)
ここで、この発想に至ったらば、「もしかしてもしかすると、だな。まさか区間縮小区法が使えるんじゃないか?」と思えるわけです。
「だって、区間縮小法はどんどん区間を狭めてって収束先を見つける手法なんだから\(f(d)=D\)に収束する\(d\)を見つけることと似てるじゃんね。」というわけです。
ネタバラシすると、中間値の定理の証明方法はいくつかあります。
筆者と同じ発想で区間縮小法で証明する方法もあれば、ワイエルシュトラスの上限公理を使った証明方法もあります。
本記事では区間縮小法を使った証明を紹介します。
いざ、証明
証明に際して、区間縮小法が使えそうだ、と思っているわけですから、「どうやって縮小する区間(どんどん小さくなる区間)を作るんだ?」ということが肝になってきます。
むしろこの区間を作ってしまえばおしまいです。
区間縮小法は何だったかと言うと、
- 任意の\(I_n\)に含まれる実数が存在する。すなわち $$\bigcap_{n\in\mathbb{N}}I_n\neq\emptyset$$,
- 特に、\(I_n=[a_n,b_n]\)として、\(\displaystyle \lim_{n\to\infty}(b_n-a_n)=0\)であれば(すなわち、区間がどんどん小さくなっていけば)、共通部分は一点\(\alpha\)のみからなる集合である。すなわち、 $$\bigcap_{n\in\mathbb{N}}I_n=\{\alpha\}$$ である。このとき、 $$\lim_{n\to\infty}a_n=\lim_{n\to\infty}b_n=\alpha$$ である。
でした。
以前区間縮小法を使った証明にはデデキントの定理やらボルツァーノ-ワイエルシュトラスの定理がありました。
これらはアルキメデスの原理を追加することで同値な定理ですが、主張としては別です。
しかし、どのように区間縮小法を使うのか、ということについては同じです。
与えられた区間の中のある点を目指して長さを半分ずつにしていくことで、どんどん小さくなる区間(縮小する区間)の列と数列を作りました。
今回もこの発想でできるのではないか?ということでやってみます。
(あくまで予想です。)
「マネしてやってみよう!」というわけです。
では行きましょう。
(証明の流れ)
- (ステップ1):デデキントの定理の証明やボルツァーノ-ワイエルシュトラスの定理を証明するときと同じような縮小する区間を作る。
- (ステップ2):区間縮小法から縮小する区間はある一点だけの集合になる。
- (ステップ3):その一点が求めたい\(d\)であることを示す。
中間値の定理の証明
(ステップ1):デデキントの定理の証明やボルツァーノ-ワイエルシュトラスの定理を証明するときと同じような縮小する区間を作る。
関数\(f:[a,b]\to\mathbb{R}\)が\([a,b]\)で連続であるとします。
どんどん小さくなる区間の列を作りたいということを念頭に置きます。
このとき、\(f(a)<D<f(b)\)を満たす任意の\(D\in\mathbb{R}\)に対して、数列\(\{a_n\}_{n\in\mathbb{N}}\)と\(\{b_n\}_{n\in\mathbb{N}}\)を以下のように決めます。
※文章だとわかりにくいかもしれないので、その際はまず以下の文章の後にある図を見てから、下記の文章を読んでみてください。
①\(n=1\)のとき、\(a_1=a\)、\(b_1=b\)とします。
どんどん小さくなる区間を作りたいので、まずは区間の端っこを使った一番大きい区間を作るためです。
このとき、\(b_1-a_1=b-a\)です。
\(a_1=a\)、\(b_1=b\)であり、尚かつ\(f(a)<D<f(b)\)ですから、
$$f(a_1)<D<f(b_1)$$
が成り立ちます。
②\(n=2\)のとき、\(a_2\)と\(b_2\)を次のように決めます。
- \(\displaystyle f\left( \frac{a_1+b_1}{2} \right)<D\)のとき
$$\begin{cases}\displaystyle
a_2=\frac{a_1+b_1}{2}\\
b_2=b_1
\end{cases}$$
とします。
このとき、\(\displaystyle f\left(\frac{a_1+b_1}{2}\right)=f(a_2)<D\)が成り立ちます。 - \(\displaystyle f\left( \frac{a_1+b_1}{2} \right)>D\)のとき
$$\begin{cases}\displaystyle
a_2=a_1\\
b_2=\frac{a_1+b_1}{2}
\end{cases}$$
とします。
このとき、\(\displaystyle f\left(\frac{a_1+b_1}{2}\right)=f(b_2)>D\)が成り立ちます。
このようにすることで、\([a,b]\)よりも小さく小さい区間を作ることができ、さらには\(f(d)=D\)を満たす\(d\)に近づきます。
1.の場合、2.の場合のいずれであっても
\begin{eqnarray}
b_2-a_2&=&\frac{1}{2}(b_1-a_1)\\
&=&\frac{1}{2}(b-a)
\end{eqnarray}
が成り立ちます。
さらに、
$$f(a_2)<D<f(b_2)$$
が成り立ちます。
もし仮に\(\displaystyle f\left( \frac{a_1+b_1}{2} \right)=D\)であったのなら、
$$d=\frac{a_1+b_1}{2}$$
ということが分かるので、証明はおしまいです。
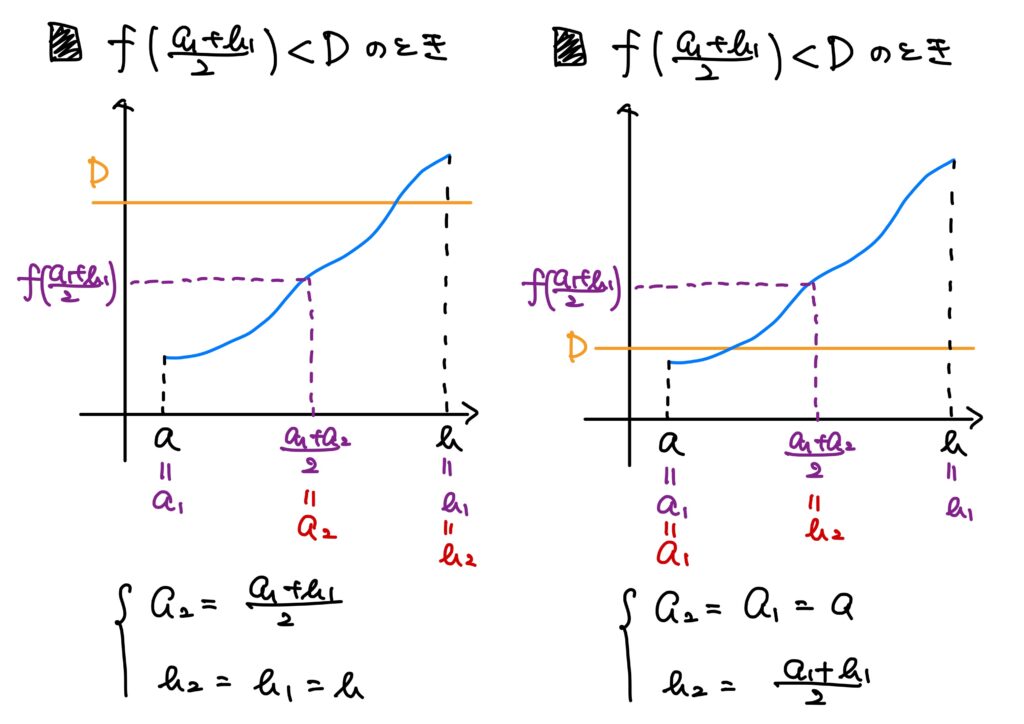
①、②と同じ手続きで数列\(\{a_n\}_{n\in\mathbb{N}}\)と\(\{b_n\}_{n\in\mathbb{N}}\)を決めます。(本質的には数列を決めるというより、その数列の値を端点とする区間を決めることになります。)
③\(n=n\)のとき
- \(\displaystyle f\left( \frac{a_{n-1}+b_{n-1}}{2} \right)<D\)のとき
$$\begin{cases}\displaystyle
a_n=\frac{a_{n-1}+b_{n-1}}{2}\\
b_n=b_{n-1}
\end{cases}$$
とします。
このとき、\(\displaystyle f\left(\frac{a_{n-1}+b_{n-1}}{2}\right)=f(a_n)<D\)が成り立ちます。 - \(\displaystyle f\left( \frac{a_{n-1}+b_{n-1}}{2} \right)<D\)のとき
$$\begin{cases}\displaystyle
a_n=a_{n-1}\\
b_n=\frac{a_{n-1}+b_{n-1}}{2}
\end{cases}$$
とします。
このとき、\(\displaystyle f\left(\frac{a_{n-1}+b_{n-1}}{2}\right)=f(b_n)>D\)が成り立ちます。 - \(\displaystyle f\left( \frac{a_{n-1}+b_{n-1}}{2} \right)=D\)のとき
\(\displaystyle d=\frac{a_{n-1}+b_{n-1}}{2}\)とすることで証明が終わります。
このときも、先と同じで1.、2.、3.の場合のうち3.の場合は既に証明が終わっていることになるので、1.、2.のいずれの場合出会ったとしても、
\begin{eqnarray}
b_n-a_n&=&\frac{1}{2}(b_{n-1}-a_{n-1})\\
&=&\frac{1}{2^{n-1}}(b-a)
\end{eqnarray}
が成り立ちます。
さらに、
$$f(a_n)<D<f(b_n)$$
が成り立ちます。
さて、これで数列\(\{a_n\}_{n\in\mathbb{N}}\)と\(\{b_n\}_{n\in\mathbb{N}}\)の値を端点とする縮小する区間が作れてような気がします。
しかし、まだ「ような気がする」だけであって、本当に縮小するのかどうかを考えなければなりません。
つまり、\(\{a_n\}_{n\in\mathbb{N}}\)が単調増加数列で\(\{b_n\}_{n\in\mathbb{N}}\)が単調減少数列であることを確かめなければなりません。
「いやいや。縮小するように作ったんだからそりゃそうでしょ。」と思うかもしれませんが、確認してみましょう。
まずは\(\{a_n\}_{n\in\mathbb{N}}\)が単調増加数列かどうかです。
- \(\displaystyle f\left( \frac{a_{n-1}+b_{n-1}}{2} \right)<D\)のとき
\(\displaystyle a_n=\frac{a_{n-1}+b_{n-1}}{2}\)です。
このとき、
\begin{eqnarray}
a_n-a_{n-1}&=&\frac{(b_{n-1}-a_{n-1})}{2}\\
&=&\frac{1}{2^{n-1}}(b-a)
\end{eqnarray}
です。
任意の\(n\in\mathbb{N}\)に対して、\(\dfrac{1}{2^{n-1}}>0\)で、かつ\(b-a>0\)ですので、\(\dfrac{1}{2^{n-1}}(b-a)>0\)です。 - \(\displaystyle f\left( \frac{a_{n-1}+b_{n-1}}{2} \right)>D\)のとき
\(a_n=a_{n-1}\)です。
従って、任意の\(n\in\mathbb{N}\)で\(a_n\geq a_{n-1}\)ですので、\(\{a_n\}_{n\in\mathbb{N}}\)は単調増加数列です。
次に\(\{b_n\}_{n\in\mathbb{N}}\)が単調減少数列かどうかです。
- \(\displaystyle f\left( \frac{a_{n-1}+b_{n-1}}{2} \right)<D\)のとき
\(b_n=b_{n-1}\)です。 - \(\displaystyle f\left( \frac{a_{n-1}+b_{n-1}}{2} \right)>D\)のとき
\(\displaystyle b_n=\frac{a_{n-1}+b_{n-1}}{2}\)です。
このとき、
\begin{eqnarray}
b_n-b_{n-1}&=&\frac{(a_{n-1}-b_{n-1})}{2}\\
&=&-\frac{1}{2^{n-1}}(b-a)
\end{eqnarray}
です。
任意の\(n\in\mathbb{N}\)に対して、\(\dfrac{1}{2^{n-1}}>0\)で、かつ\(b-a>0\)ですので、\(-\dfrac{1}{2^{n-1}}(b-a)<0\)です。
従って、任意の\(n\in\mathbb{N}\)で\(b_n\leq b_{n-1}\)ですので、\(\{b_n\}_{n\in\mathbb{N}}\)は単調減少数列です。
これでようやく、「数列\(\{a_n\}_{n\in\mathbb{N}}\)と\(\{b_n\}_{n\in\mathbb{N}}\)の値を端点とする縮小する区間が作れた。」と断言できます。
さらに、\(b_n-a_n=\dfrac{1}{2^{n-1}}(b-a)\)ですので、
$$
\lim_{n\to\infty}(b_n-a_n)=\lim_{n\to\infty}\frac{1}{2^{n-1}}(b-a)=0
$$
(ステップ2):区間縮小法から縮小する区間はある一点だけの集合になる。
さて、これで区間縮小法の仮定を満たしたことになります。
つまり、
$$\lim_{n\to\infty}a_n=\lim_{n\to\infty}b_n=\alpha$$
という\(\alpha\in\mathbb{R}\)が存在します。
もともとは縮小する区間を作ってどんどん範囲を狭めることによって\(d\)を見つけたいな、という話でしたので、もしこの\(\alpha\)が\(d\)の正体であれば嬉しいわけです。
というか証明が終わります。
要は、\(f(\alpha)=D\)を証明したいわけです。
(ステップ3):\(\alpha=d\)を示す。
「どうしよっかな」となるわけですが、\(\displaystyle\lim_{n\to\infty}a_n=\lim_{n\to\infty}b_n=\alpha\)なのですから、\(\displaystyle f(\lim_{n\to\infty}a_n)=D\)を示せば良いことになります。
そこで、まだ使っていない事実\(f(a_n)<D<f(b_n)\)に着目します。
すると、
\begin{eqnarray}
\lim_{n\to\infty}f(a_n)<\lim_{n\to\infty}D<\lim_{n\to\infty}f(b_n)\Leftrightarrow \lim_{n\to\infty}f(a_n)<D<\lim_{n\to\infty}f(b_n)
\end{eqnarray}
ですので、仮に\(\displaystyle \lim_{n\to\infty}f(a_n)=f\left(\lim_{n\to\infty}a_n\right)\)だったらば、
\begin{eqnarray}
\lim_{n\to\infty}f(a_n)<D<\lim_{n\to\infty}f(b_n)&\Leftrightarrow&f\left(\lim_{n\to\infty}a_n\right)<D<f\left(\lim_{n\to\infty}b_n\right)\\
&\Leftrightarrow&f(\alpha)<D<f(\alpha)\\
&\Leftrightarrow&f(\alpha)=D
\end{eqnarray}
となります。
これは個人の視点に依りますが、筆者は
「連続な関数だったら、定義域内のどの点でも必ず関数の値が1つだけ定まっていて、しかもその値が飛び値でもないわけだから、定義域内の数列の極限とその極限での関数の値が一致しそうだな。でも飛び値があるような不連続な関数だったら必ずしも一致しないな。」
と思うので、本当に正しいかどうか証明してみます。
補題の証明
示したいことは
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n>N\Rightarrow |f(x_n)-f(a)|<\epsilon)$$
です。
毎度のことで\(\delta\)を見つけてきましょう。
まず、\(f\)は\(I\)で連続なので、\(a\in I\)でも連続です。
従って、
$$(\forall \epsilon>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall x\in I:0<|x-a|<\delta_1\Rightarrow |f(x)-f(a)|<\epsilon)$$
が成り立ちます。
また、数列\(\{x_n\}_{n\in\mathbb{N}}\)は\(a\)に収束するので、
$$(\forall \epsilon_2>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |x_n-a|<\epsilon_2)$$
が成り立ちます。
この\(\epsilon_2\)は任意の正の実数ですので、\(\epsilon_2=\delta_1\)でも成り立ちます。
すなわち、
$$(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n\geq N\Rightarrow |x_n-a|<\delta_1)$$
が成り立っています。
このとき\(x_n\in I\)で、尚つ\(|x_n-a|<\delta_1)\)が成り立っているので、\(|f(x_n)-f(a)|<\epsilon\)が成り立ちます。
すなわち、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}:n>N\Rightarrow |f(x_n)-f(a)|<\epsilon)$$
です。
補題の証明終わり
さて、戻りましょう。
今、補題から\(\displaystyle \lim_{n\to\infty}f(a_n)=f\left(\lim_{n\to\infty}a_n\right)\)が分かりました。
従って
\begin{eqnarray}
\lim_{n\to\infty}f(a_n)<D<\lim_{n\to\infty}f(b_n)&\Leftrightarrow&f\left(\lim_{n\to\infty}a_n\right)<D<f\left(\lim_{n\to\infty}b_n\right)\\
&\Leftrightarrow&f(\alpha)<D<f(\alpha)\\
&\Leftrightarrow&f(\alpha)=D
\end{eqnarray}
が成り立ちました。
以上のことから\(f(\alpha)=D\)が分かったので、\(d\)の正体は\(\alpha\)だったことが分かります。
従って、中間値の定理が成り立ちます。
中間値の定理の証明終わり
結
今回は中間値の定理の証明を説明しました。
中間値の定理というのは
ということで、証明には複数の手法がありますが、今回は区間縮小法で証明しました。
次回は関数の連続性から得られるもう一つの有名な定理、平均値の定理のイメージについて解説します。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ1冊持っておくと良いと思います!






コメントをする