本記事の内容
本記事は、基本情報技術者試験におけるデータの単位、コンピュータでの数の数え方について、情報及びコンピュータの素人目線から説明する記事です。
本記事を読むに当たり、2進数、16進数について知っている必要があるため、以下の記事も合わせてご覧ください。

本記事のゴール
本記事のゴールは次の問題を解けるようになることです。
10進数の演算式\(7\div 32\)の結果を2進数で表したものはどれか。
ア. 0.001011 イ. 0.001101 ウ. 0.00111 エ. 0.0111
(平成31年度)
基数変換
基本情報技術者試験の対策をしていて、まず最初に躓くであろう部分(筆者は躓きました)が基数変換だと思います。
読んで字の如し、基数を変換するやり方です。
ただ、基数がわかっていればなんてことありません。
16進数→10進数、10進数→2進数の変換さえできれば、10進数→16進数の変換も本質的に同じであるため十分です。
16進数→10進数
2BD.C8という16進数表現の数を10進数表現に変換せよ。
簡単です。
16進数表現の2BD.C8という数は、
$$
2\times16^{2}+{\rm B}\times16^{1}+{\rm D}\times16^0+{\rm C}\times16^{-1}+8\times16^{-2}
$$
でした。
そして、B、C、Dはそれぞれ10進数表現では11、12、13です。
故に、
\begin{eqnarray}
2{\rm BD}.{\rm C}8&=&2\times16^{2}+{\rm B}\times16^{1}+{\rm D}\times16^0+{\rm C}\times16^{-1}+8\times16^{-2}\\
&=&2\times16^{2}+11\times16^{1}+13\times16^0+12\times16^{-1}+8\times16^{-2}\\
&=&512+176+13+\frac{12}{16}+\frac{8}{16^2}\\
&=&701.78125
\end{eqnarray}
となるわけです。
10進数→2進数
10進数表現の4.625を2進数表現に直す方法を述べます。
(ここでは手法を述べることに留めます)
やることは簡単で、与えられた数を整数部と小数部に分け、それぞれ変換します。
整数部
単純です。
10進数を2進数の基数2で割り算を商が0になるまで続け、余りを逆に並べる
だけです。
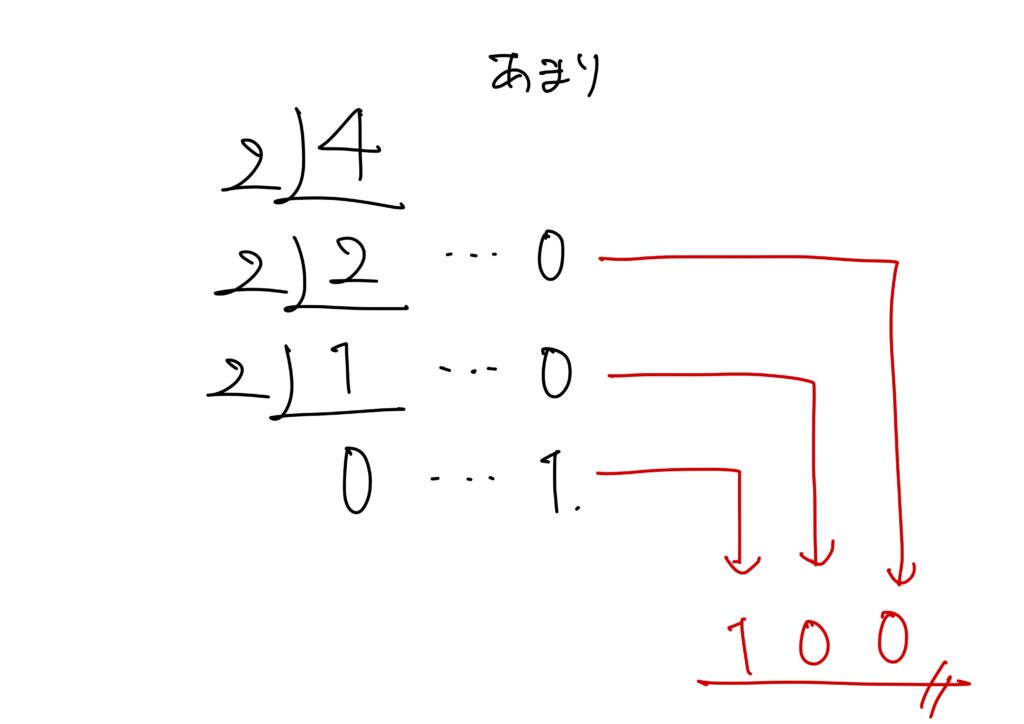
小数部
- 10進数小数に、2進数の基数2をかける。
- 積のうち、整数部だけを取り出す。
- 残った小数に更に2をかける。
これを小数部が0になるまで続けます。
本記事のゴールを解いてみる
10進数の演算式\(7\div 32\)の結果を2進数で表したものはどれか。
ア. 0.001011 イ. 0.001101 ウ. 0.00111 エ. 0.0111
(平成31年度)
まず、\(7\div 32=0.2185\)です。
整数部は0ですので、小数部だけを変換します。

負の2進数
負の整数を2進数で表現する方法には以下の3つがあります。
- 絶対値表現
- 1の補数表現
- 2の補数表現
絶対値表現
絶対値表現
ビット列の先頭の1ビットで「正負」を表し、残りのビットで「値」を表す方法。先頭の1ビットが0の場合は「正」を表し、1の場合は「負」を表す。例2. 8ビットの2進数で表現
- \(2=00000010\)
- \(-2=10000010\)
1の補数表現
1の補数表現
1の補数表現とは、全てのビットを反転することで正負を表す方法。ただし、反転とは、0を1に、1を0に変換することである。例3. 8ビットの2進数で表現
- \(2=00000010\)
- \(-2=11111101\)
2の補数表現
2の補数表現
全てのビットを反転した後に、1を足して正負を表現する方法。例4. 8ビットの2進数で表現
- \(2=00000010\)
- \(-2=11111110\)
結
今回は、基本情報技術者試験における基数変換、負の2進数について、情報及びコンピュータの素人目線から説明しました。
問題が解けるということに重きを置き説明しました。
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければお答えします!
Twitterでもリプ、DM問わず質問、コメントを大募集しております!



コメントをする