本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題を1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。
前回の問題については以下の記事を御覧ください!
問題を明示します。
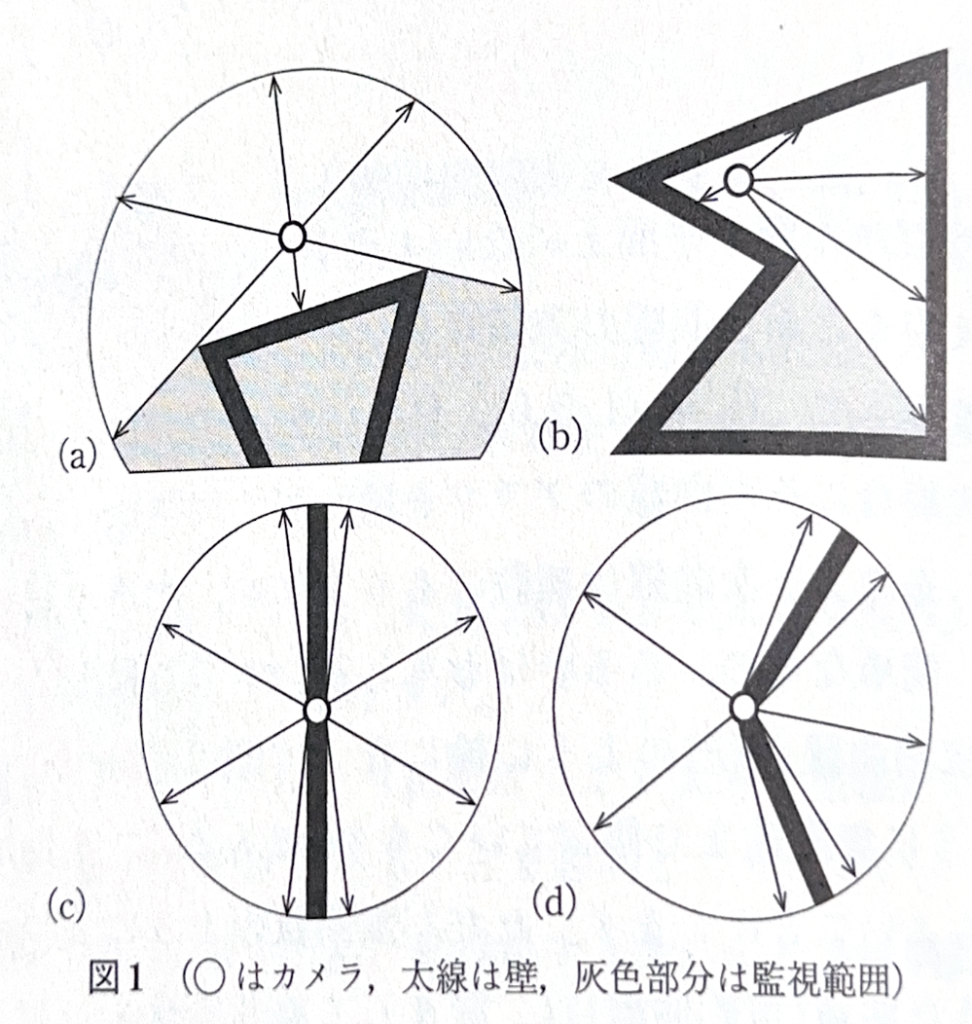
平面上に\(n\)角形(凸とは限らない)の形をした図形がある。この図形を刑務所の平面図と見なすことにしよう。平面上の適切な位置に何台かの監視用カメラを設置し、刑務所の内部と外部の両方を監視したい。ただし、カメラが監視できる範囲を次のように定めます:
(1) さえぎる壁がない限り、カメラの視線は、その位置を中心として\(360^\circ\)の範囲を監視できる(図1(a),(b)参照)。
(2) 壁に設置されたカメラは壁の両側とも(内側も外側も)監視できる(図1(c),(d)参照)。
さて、刑務所の形がどんな形をした\(n\)角形であろうとも、平面全体を監視するために、高々\(\displaystyle \left\lfloor\frac{n+2}{2}\right\rfloor\)\(\Bigg(\)\(\displaystyle\frac{n+2}{2}\)の切り下げ\(\Bigg)\)台のカメラを適切な位置に設置すれば十分であることを証明して下さい。ただし、この問題は全て平面の問題としてと考えることにします。
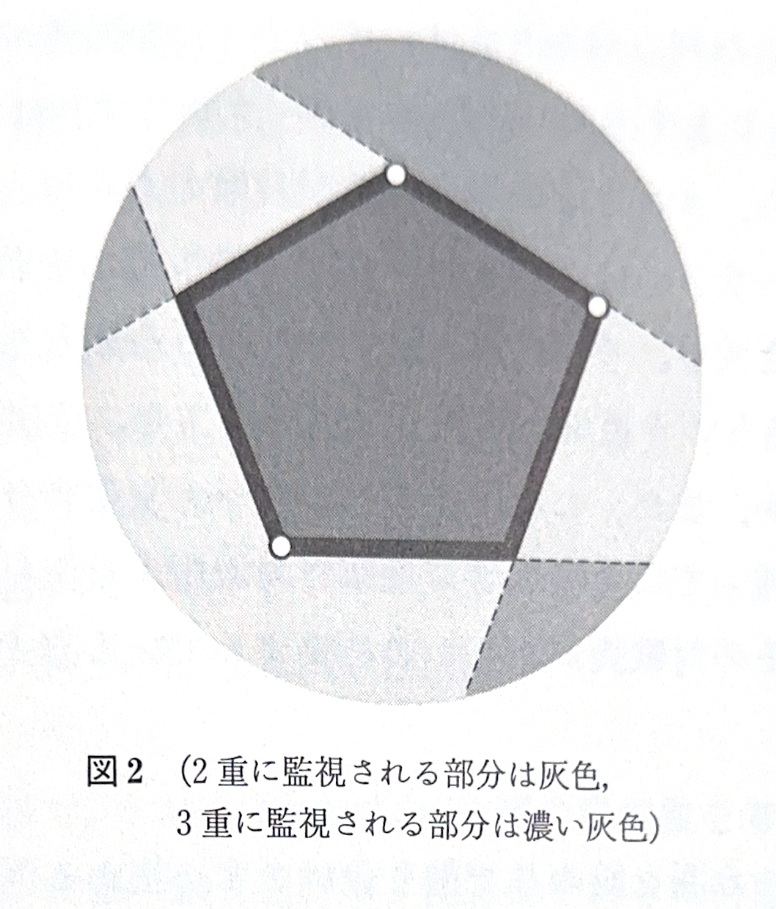
たとえば、図2のように、5角形の形をした刑務所ならば3台以上のカメラが必要です。数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p25.
チャレンジの結果…?
チャレンジの結果…解けませんでした…
最近解けない状態が続き、少々悲しいです…
筆者の解答を紹介します。
この問題を読んだときに、次の2つをパッと思いつきました。
- 数学的帰納法で攻めるか?
- 四色問題と関係がありそう?
正直、四色問題の方は「やってみて使いそうなら使うか」程度でした。
というわけで、数学的帰納法で攻めてみることにしました。
\(1\)角形および\(2\)角形は問題文の図(c)と(d)で示されているため、\(n\geq3\)の場合を考えます。
\(n=3\)のとき
\(n=3\)のときは、三角形しかありえません。
このとき、カメラを置くことができる位置の候補は次の10個です。
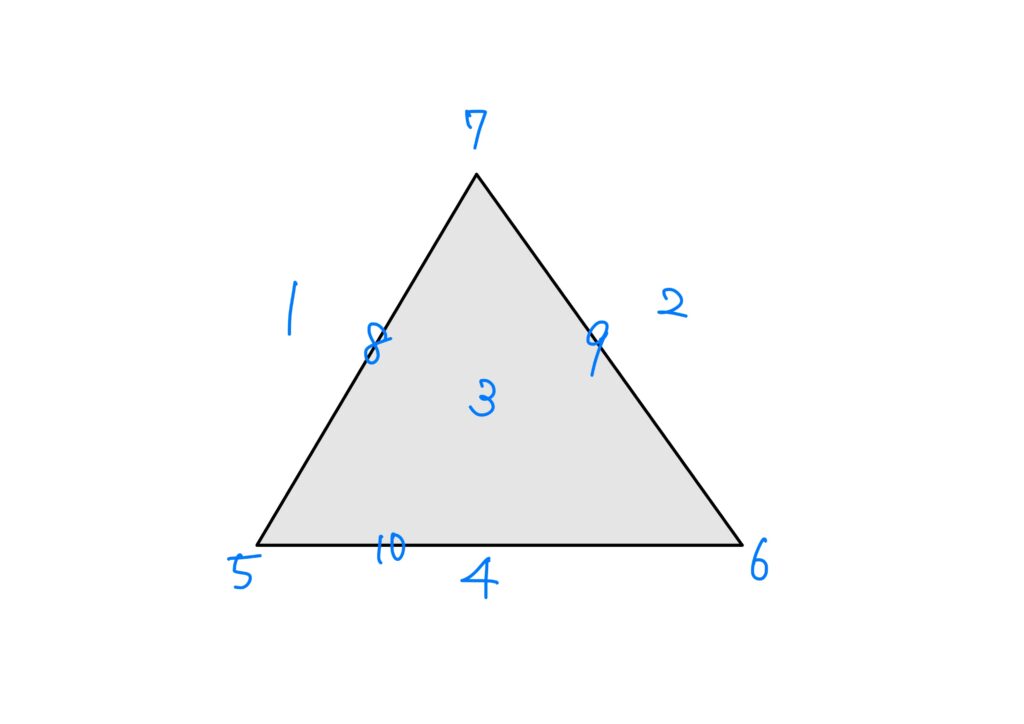
このとき、カメラを置く位置をその位置の番号の組で表したとします。
すると、\((7,4)\)か\((5,2)\)か\((6,1)\)に置けば十分であることがわかります。
仮に、\(1\)から\(10\)のうち、どの1つを選んだとしても必ず死角が生まれることもわかります。
つまり、\(n=3\)の場合はカメラを2個置けば十分であることがわかります。
そして、
$$
2=\left\lfloor \frac{3+2}{2}\right\rfloor=\left\lfloor \frac{5}{2}\right\rfloor=\lfloor 2.5\rfloor
$$
となるため、題意を満たします。
一応、\(n=4\)の場合も確認しましたが、題意を満たすことを同様に証明できます。
ちなみに、\(n=4\)の場合も2個で十分です(対角線の頂点の2個に置けばよい)。
\(n=k+1\)のとき
\(n=k\)のときに成り立つと仮定します。
すなわち、\(k\)角形領域全体を監視するには高々\(\displaystyle\left\lfloor \frac{k+2}{2}\right\rfloor\)個のカメラがあれば十分であるとします。
その上で\(n=k+1\)の場合を考えます。
このとき、次の場合に分けることができます。
- \(k\)角形が凸多角形\(\land\)\(k+1\)角形が凸多角形
- \(k\)角形が凸多角形\(\land\)\(k+1\)角形が凸多角形でない
- \(k\)角形が凸多角形でない\(\land\)\(k+1\)角形が凸多角形
- \(k\)角形が凸多角形でない\(\land\)\(k+1\)角形が凸多角形でない
1.\(k\)角形が凸多角形\(\land\)\(k+1\)角形が凸多角形である場合
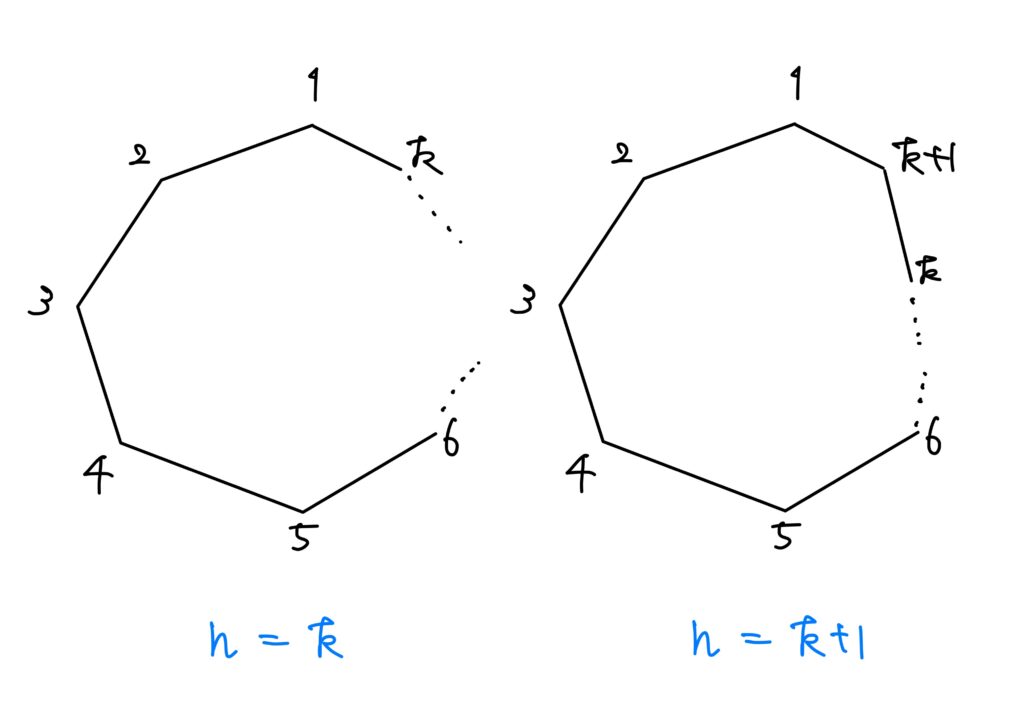
\(n=k\)のとき、一般性を失わず頂点1にカメラが置いてあると仮定してOKです。
すると、頂点1に置いているカメラ(これをカメラ1と呼ぶ)は下図のように
- \(k\)角形の内部
- 辺\((1,2)\)および辺\((k,1)\)の外部
の領域を網羅しています。
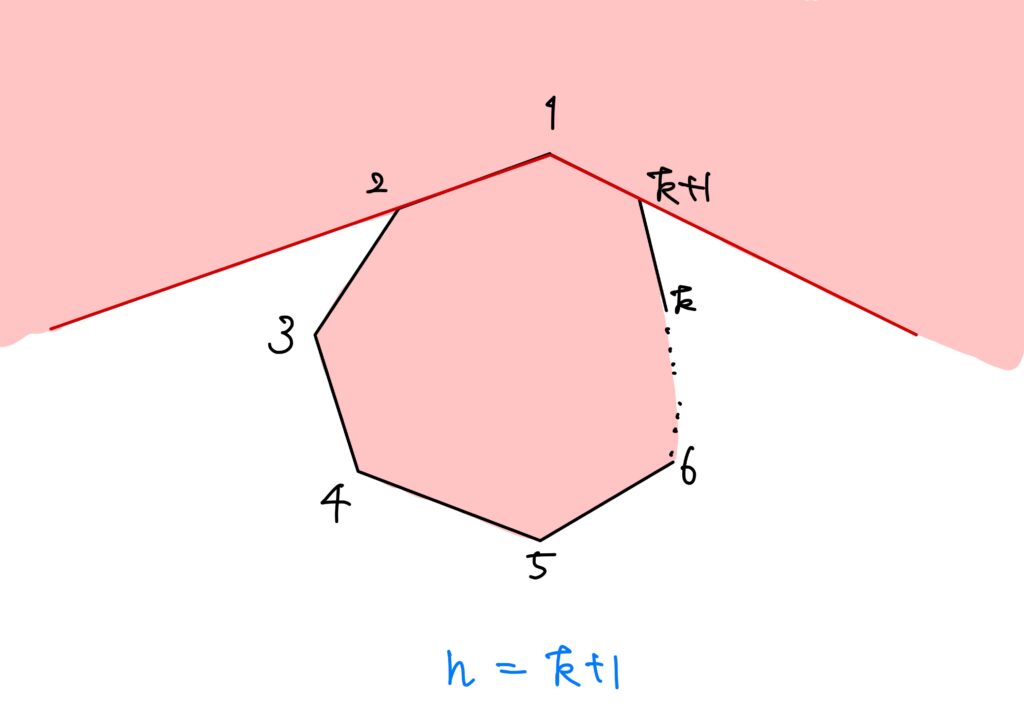
この事実はカメラを置いた頂点に対して、その頂点から映える隣接した二辺の外部と多角形の内部を網羅していることを指していて、頂点上にカメラが設置されていれば、位置(頂点の番号)に依存しません。
故に、\(3,5,7,9,\cdots\)とカメラを置いていけばOKです。
つまり、\(\displaystyle\left\lfloor \frac{k}{2}\right\rfloor\)個あれば十分です。
\(n=k+1\)の場合も全く同様で\(\displaystyle\left\lfloor \frac{k+1}{2}\right\rfloor\)個あれば十分です。
そして、
$$
\left\lfloor \frac{k+1}{2}\right\rfloor\leq \left\lfloor \frac{k+2}{2}\right\rfloor
$$
だから、題意を満たします。
2.\(k\)角形が凸多角形\(\land\)\(k+1\)角形が凸多角形でない場合
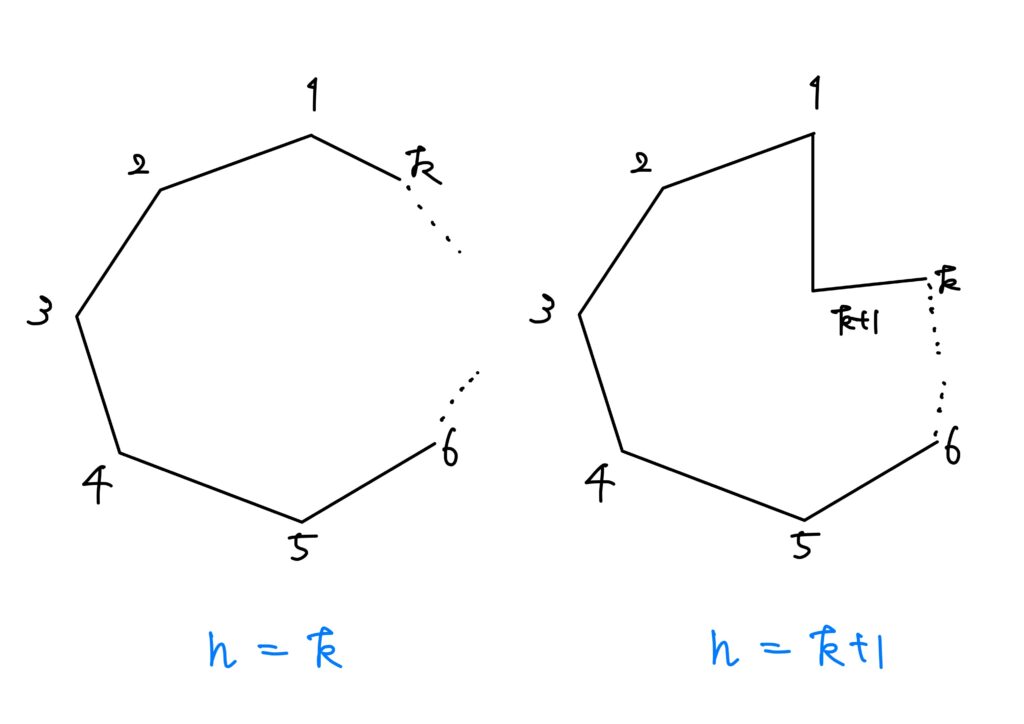
要するに、頂点\(k+1\)の部分だけ凹んでいるという状況です。
まず、頂点\(1\)にカメラを置きます。
すると、そのカメラは以下の領域を網羅しています。
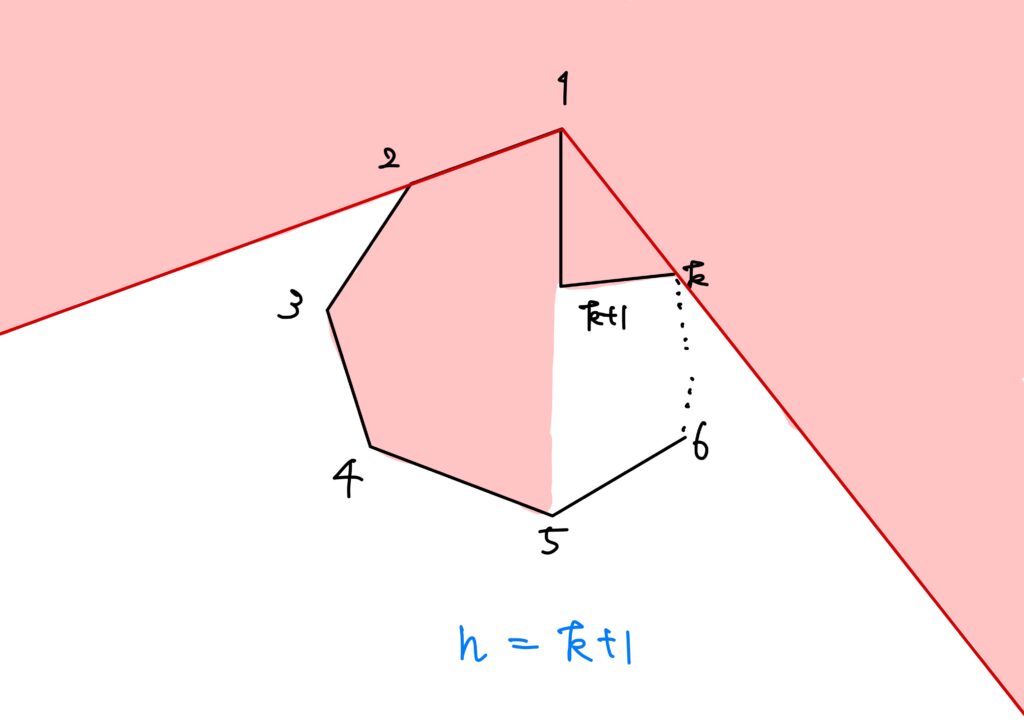
カメラ\(1\)で網羅されている頂点を\(l\)個とすると、網羅されていない頂点は\(k+1-l\)個です。
このとき、カバーされている頂点に対しては\(\displaystyle\left\lfloor \frac{l}{2}\right\rfloor\)個あれば、その\(l\)個の頂点の外部は網羅できます。
同様にして、カメラ\(1\)で網羅されていない頂点に対しては\(\displaystyle\left\lfloor \frac{k+1-l}{2}\right\rfloor\)個あれば十分です。
したがって、
$$
\left\lfloor \frac{l}{2}\right\rfloor+\left\lfloor \frac{k+1-l}{2}\right\rfloor\leq\left\lfloor \frac{k+3}{2}\right\rfloor
$$
を示せばOKです。
床関数の性質から、
\begin{eqnarray}
&&\frac{l}{2}-1<\left\lfloor \frac{l}{2}\right\rfloor\leq \frac{l}{2}\\
&&\frac{k+1-l}{2}-1<\left\lfloor \frac{k+1-l}{2}\right\rfloor\leq\frac{k+1-l}{2}
\end{eqnarray}
であるため、
$$
\frac{l}{2}+\frac{k+1-l}{2}-2<\left\lfloor \frac{l}{2}\right\rfloor+\left\lfloor \frac{k+1-l}{2}\right\rfloor\leq\frac{l}{2}+\frac{k+1-l}{2}
$$
が成り立ちます。
これを変形すれば、
$$
\frac{k-3}{2}<\left\lfloor \frac{l}{2}\right\rfloor+\left\lfloor \frac{k+1-l}{2}\right\rfloor\leq\frac{k+1}{2}
$$
です。
一方で、
$$
\frac{k+3}{2}-1<\left\lfloor \frac{k+3}{2}\right\rfloor\leq\frac{k+3}{2}
$$
です。
すなわち、
$$
\frac{k+2}{2}<\left\lfloor \frac{k+3}{2}\right\rfloor\leq\frac{k+3}{2}
$$
です。
以上から、\(\displaystyle\left\lfloor \frac{l}{2}\right\rfloor+\left\lfloor \frac{k+1-l}{2}\right\rfloor\)と\(\displaystyle\left\lfloor \frac{k+3}{2}\right\rfloor\)の範囲は共通部分を持たずに、後者が真に大きいことがわかります。
したがって、題意を満たします。
3.\(k\)角形が凸多角形でない\(\land\)\(k+1\)角形が凸多角形の場合
ここで詰まりました。
なぜなら、\(k\)角形に何個の凹んでいる点があるかで細かく場合分けしなければならないからです。
ココまで来て、この手法は良くないのだなーと感じました。
それでも何かできないかなと悩みましたが時間切れです。
投稿されたエレガントな解答
(前略)
この問題を出題する際に、問題文の中に“4色定理を用いて次の命題を証明せよ”と書き加えるべきか否かについて悩みました。そして、最終的には、この刑務所問題に真剣に取り組めば、きっと、4色定理(平面上のどんな地図も、隣り合うどの2か国も異なる色になるように、4色の色で塗り分けることができる(Appel & Hakrn, 1976))が脳裏をかすめるでしょうし、さらに、もし、“4色定理を用いて証明せよ”とするとやさしすぎるということになりかねないと判断し、結局、問題文中では4色定理を使うことを示唆しないことにしたのでした。この判断が、正解者1名という悲しい結果を招いた原因であると反省しています。
正解者は1名で、不正解のほとんどが「\(n\)角形の頂点\({\rm P}_1,{\rm P}_2,\cdots,{\rm P}_n\)の偶数(または奇数)番目(すなわち、1つおき)にカメラを設置すれば良い。」という解答で、その証明を、\(n\)角形のいち部分に着目して場合分けしたり、昨日法を用いて示そうとしていました。しかしながら、\(n\)角形の形が多様で、上の方針による証明は不可能そうです。
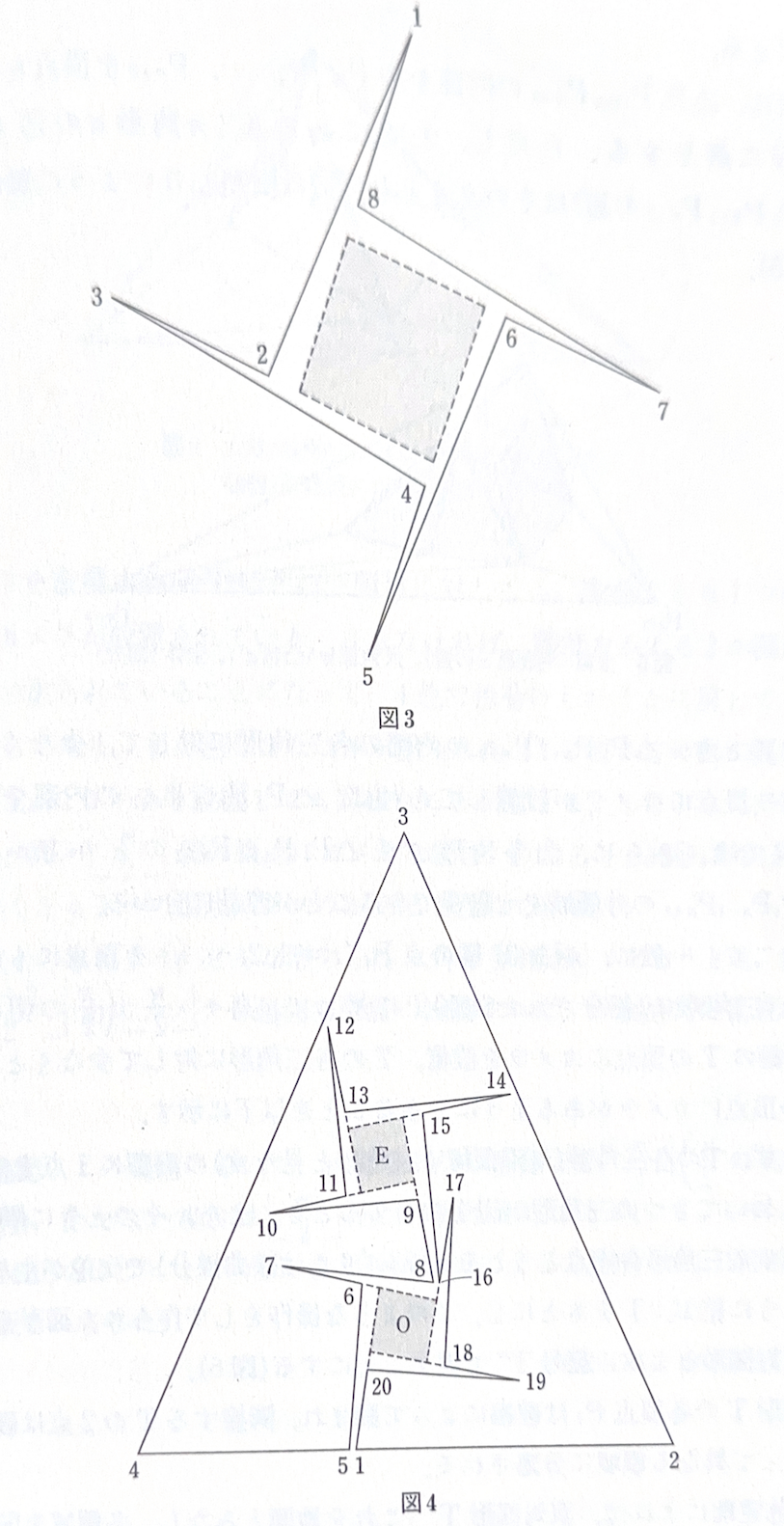
そこで、まず、カメラを多角形の頂点に1つおきに配置しても平面全体を監視できない例を示しましょう。図3は(中略)氏によるものですが、頂点1,3,5,7のいちにカメラを配置しても内側のある部分(灰色部分)が監視できない例です。これを組み合わせると、図4のように外側を監視できない例も作れます。図4において、領域\({\rm E}\)、\({\rm O}\)はそれぞれ、カメラを多角形の偶数番目、奇数番目の点に設置しただけれは監視できない領域(死角)を表しています。 それでは、4色定理を用いて、朝エレガントに解いてくれた(中略)氏の解答を紹介しましょう。
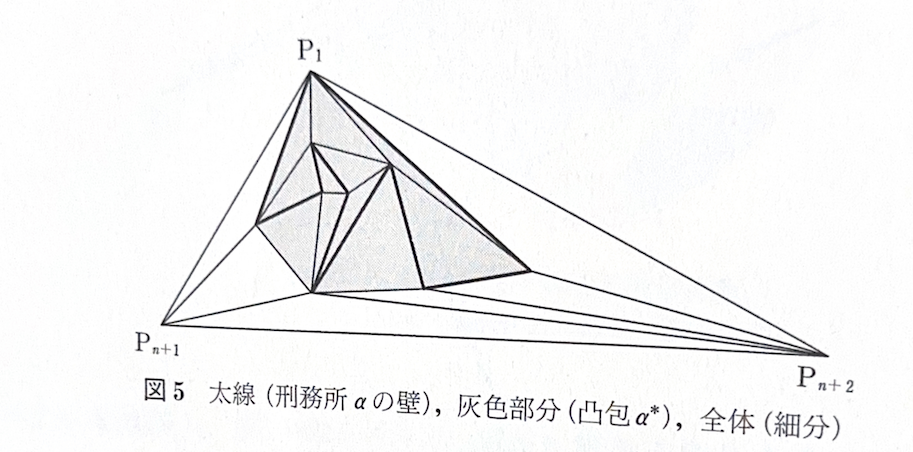
[証明] \(n\)角形\(\alpha\)を含む最小の凸多角形(凸包)を\(\alpha^\ast\)とする。\(\alpha^\ast\)の協会乗の1点を\({\rm P}_1\)としたとき、\(\alpha^\ast\)の外部の2点\({\rm P}_{n+1},{\rm P}_{n+2}\)を\(\triangle{\rm P}_1{\rm P}_{n+1}{\rm P}_{n+2}\)が\(\alpha^\ast\)を完全に内部に含む(点\({\rm P}_1\)のみが\(\alpha^\ast\)と接する)ようにとる。
次に、\(\triangle{\rm P}_1{\rm P}_{n+1}{\rm P}_{n+2}\)の内部を点\({\rm P}_1,{\rm P}_2,\cdots,{\rm P}_{n+2}\)を頂点とする三角形に細分する。ただし、すでにある辺(\(n\)角形\(\alpha\)の辺または\(\triangle{\rm P}_1{\rm P}_{n+1}{\rm P}_{n+2}\)の辺)はそのままとし、辺は交差しないように細分する(図5)。
このとき、\(\triangle{\rm P}_1{\rm P}_{n+1}{\rm P}_{n+2}\)の内部の各三角形に対して、少なくとも1つの頂点にカメラが設置してあれば、\(\triangle{\rm P}_1{\rm P}_{n+1}{\rm P}_{n+2}\)の内部全体を監視でき、さらに、凸多角形\(\alpha^\ast\)と\(\triangle{\rm P}_1{\rm P}_{n+1}{\rm P}_{n+2}\)のとり方から、\(\triangle{\rm P}_1{\rm P}_{n+1}{\rm P}_{n+2}\)の外領域をも監視できることが容易に分かる。
そこで、一般に、\(n(\geq3)\)個の点\({\rm P}_i\ (i=1,2,\cdots,n)\)を頂点にもつような(三角形に)細分された図形\({\rm T}\)に対して、高々\(\displaystyle\left\lfloor \frac{n}{2}\right\rfloor\Large(\frac{n}{2}\)の切り下げ\(\Large)\)個の\({\rm T}\)の頂点カメラを設置、\({\rm T}\)の各三角形に対して少なくとも1つの頂点にカメラがあるようにできることをいかに示す。
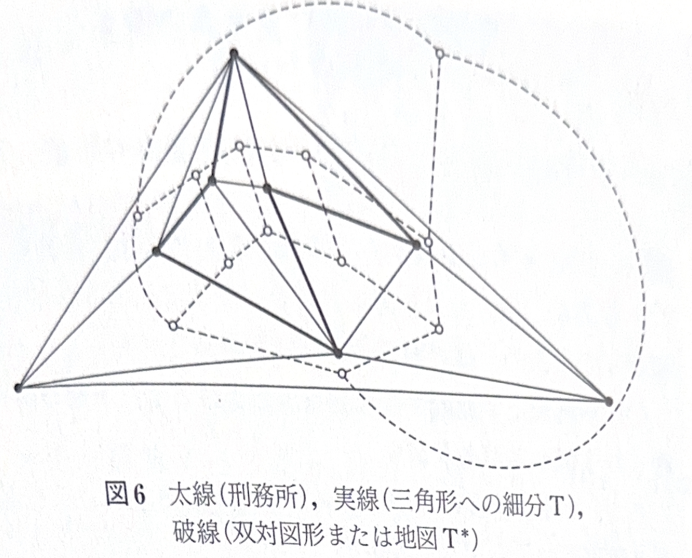
まず、\({\rm T}\)の各三角形(無限領域も三角形と見なす)の内部に1点をとり、\({\rm T}\)において2つの三角形が辺を共有するとき、また、そのときに限り、対応する三角形のない点どうしを破線分(破曲線分)で交差が生じないように結ぶ。\({\rm T}\)をもとにし、このような操作をして作られた図形を\({\rm T}\)の双対図形とよび、記号\({\rm T}^\ast\)で表すことにする(図6)。
図形\({\rm T}\)の書く頂点\({\rm P_i}\)は破線によって囲まれ、隣接する\({\rm T}\)の2点は破線によって異なる領域に分離される。
4色定理によれば、双対図形\({\rm T}^\ast\)(これを地図とみなし、各領域を国とみなせば地図色分け問題と考えることができる)を、隣接するどの2か国もことなる色になるように、4つの色1,2,3,4によって、色分けできる。そこで、色1または色2が塗られた\({\rm T}^\ast\)のすべての国に属する頂点\({\rm P}_i\)に
カメラを設置すれば\({\rm T}\)のどの三角形にたいしても、少なくとも1つの頂点にカメラが設置されている。さもなければ、隣接するある2か国が同じ色で塗られていることになって、4色で色分けしたことに反してしまうからである。また色3または色4が塗られた\({\rm T}^\ast\)のすべての国に属する頂点\({\rm P}_i\)にカメラを設置しても同様なことが言える。したがって、図形\({\rm T}\)の、高々\(\displaystyle\left\lfloor \frac{n}{2}\right\rfloor\)個の頂点にカメラを置き、\({\rm T}\)のどの三角形に対しても少なくとも1つの頂点にカメラがあるようにできる。
以上の事実より、どんな形をした\(n\)角形(刑務所)であろうとも、高々\(\displaystyle\left\lfloor \frac{n+2}{2}\right\rfloor\)台のカメラを適切な位置に設置すれば、平面全体を監視できる。
(後略) 数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p231-p235.
読者の皆様への挑戦状!
来週の日曜日に挑戦します!
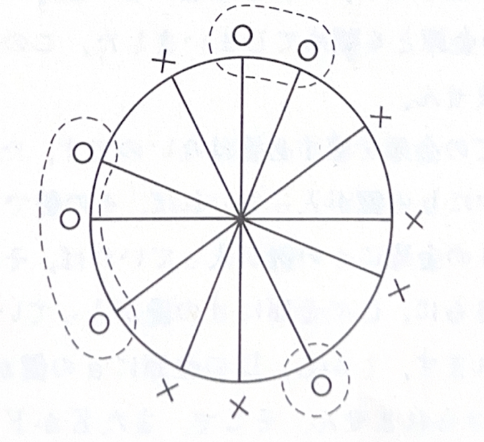
円と\(n\)本の直径からなる図形をかきます。各直径の両端について、片方に○印、もう片方に✕印をつけます。どちらを○印にするかは確率\(1/{2}\)で決め、他の直径の印付とは独立であるとします。
○印が演習場で連続する部分を島とよびます。下図の例では、点線で囲った3個の島があります。
さて、\(n\)本の直径に印付をおこなったとき、ちょうど\(k\)個の島ができる確率はいくらでしょうか?数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p27.
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ一週間ほどでお答えします。
(難しかったらもう少しかかるかもしれませんが…)
Twitterでもリプ、DM問わず質問、コメントを大募集しております!
他の「エレガントな解答をもとむ」の問題に挑戦してみたい方はぜひ以下の書籍をお買い求め下さい!




コメントをする