本記事の内容
本記事は「逆写像って?」ということについて解説する記事である。
本記事を読むにあたり、全単射と合成写像について知っているとより理解が進むと思われるので、その際は以下の記事を御覧ください。
逆写像
逆?
全単射の節で少々ネタバラシしたのだが、全単射であるときに限り逆写像(逆関数)が存在する。
高校数学では「逆関数を求めなさい。」という問題を解いたことがあると思われるが、逆写像(逆関数)は必ずしも存在するわけではない。
しかし、高校数学ではそれを学ばない(範囲外のため)、「逆関数を求めろ?んなもん簡単だろ。\(y=f(x)\)を\(x=\)の形にして最後に\(x\)と\(y\)を入れ替えればいいんだから。」で終わってしまう。
さて、逆写像という概念は至ってシンプルである。
というのも、「\(X\)の要素から\(Y\)の要素への対応があるんだったら、同じ規則で\(Y\)の要素から\(X\)の要素への対応もあるんじゃね?」という発想だからである。
つまり、「今までは\(x\)と\(f(x)\)の対応を考えていたけど、今度は\(f(x)\)から\(x\)への対応を考えてみようぜ」ということで、\(f(x)\)から\(x\)への対応というのは、”\(f(x)\)から\(x\)に戻る”写像ということである。
しかし、写像\(f\)というのは終域\(Y\)の要素が全て使われていなくても良い。
一方\(Y\)の要素から\(X\)の要素に写像\(g\)を定めるためには\(Y\)の要素を全て使う必要がある。
従って、\(X\)の要素全てと\(Y\)の要素全てに対応関係がある全単射の場合でなければ写像\(f\)と逆の対応(写像)、すなわち、”元にに戻す”対応\(g\)は考えられないのである。
\(f\)が全単射であるとき\(f\)とこの\(g\)は逆写像の関係にある、と言ったりする。
しかしながら、”もとに戻さなくて良い”のであれば、\(f:X\to Y\)とは全く関係なく、\(g:Y\to X\)という写像を(\(X\)と\(Y\)の要素が無限個なら)いくらでも作ることはできる。
これらはあくまで別々の写像なのであって、逆写像の関係にはない。
実際、\(X=\mathbb{R}\)、\(Y=\{x\in \mathbb{R}\mid x\geq 0\}\)のとき、\(f:X\to Y\)を\(f(x)=x^2\)とする。
このとき、\(f\)は全射であるが、単射ではない。
さらに、\(g:Y\to X\)を\(g(y)=y\)とすると、確かに\(g\)は\(Y\)から\(X\)への写像であるのだが、”もとには戻らない”ので\(f\)とは逆写像の関係にはない。
とどのつまり、\(f\)の逆写像というのは
ということなのである。
恒等写像
逆写像を厳密に語るために1つ特別な写像のお話をする。
と言っても非常に簡単で、\(X\neq\emptyset\)であるとき\(f:X\to X\)において、つまり自分から自分への写像であって、\(X\)の要素はすべて自分自身と対応づける、という対応である。
この写像を\(X\)の恒等写像という。
\(X=\mathbb{R}\)のとき、\(f:X\to X\)を\(f(x)=x\)とすると恒等写像である。
これは中学数学でよく出る1次関数\(y=x\)である。
以上のことを式で書けば、
で、逆写像って厳密に何よ?
逆写像というのは「\(f(x)\)を\(x\)に戻すような写像」のことであった。
これを合成写像の概念を思い出してみれば、別の言い方をすることができるのである。
それは、「\(x\)を\(f(x)\)に対応させた後、\(f(x)\)を\(x\)に戻すような写像」である。
もう少々詳しく言うと、逆写像は「\(x\)を\(f\)で\(f(x)\)に対応させた後、\(f(x)\)に\(x\)に戻すように対応させたとき、元の\(x\)に戻ってくる写像」ということなのである。
これはまさに、というわけなのである。「\(f\)と\(f(x)\)に\(x\)に戻すように対応\(g\)を合成すると、恒等写像だ!」
というわけなのである。
以上のことを式で書くと次である。

例1.
\(X=\{カレー,ステーキ、おにぎり,チャーハン\}\)、\(Y=\{スプーン,ナイフ,手,足\}\)とし、
に対して、\(h:X\to Y\)を
- \(h(カレー)=スプーン\)、
- \(h(ステーキ)=ナイフ\)、
- \(h(おにぎり)=手\)、
- \(h(チャーハン)=スプーン\)
で定めた。
しかし、足\(\in Y\)と対応する\(X\)の要素が無いし、スプーンの対応先がカレーとチャーハンの2つあるため、\(h_1:Y\to X\)をどのように定めても\(h_1\)は逆写像になりえない。
実際、スプーンをカレーに、ナイフをステーキに、手をおにぎりに、スプーンをチャーハンに対応させるためには
- \(h_1(スプーン)=カレー\)、
- \(h_1(ナイフ)=ステーキ\)、
- \(h_1(手)=おにぎり\)、
- \(h_1(スプーン)=チャーハン\)
としなければならないのだが、なんとスプーンにはカレーとチャーハンの2つの対応先が存在することになり、\(h_1\)は写像でないためである。

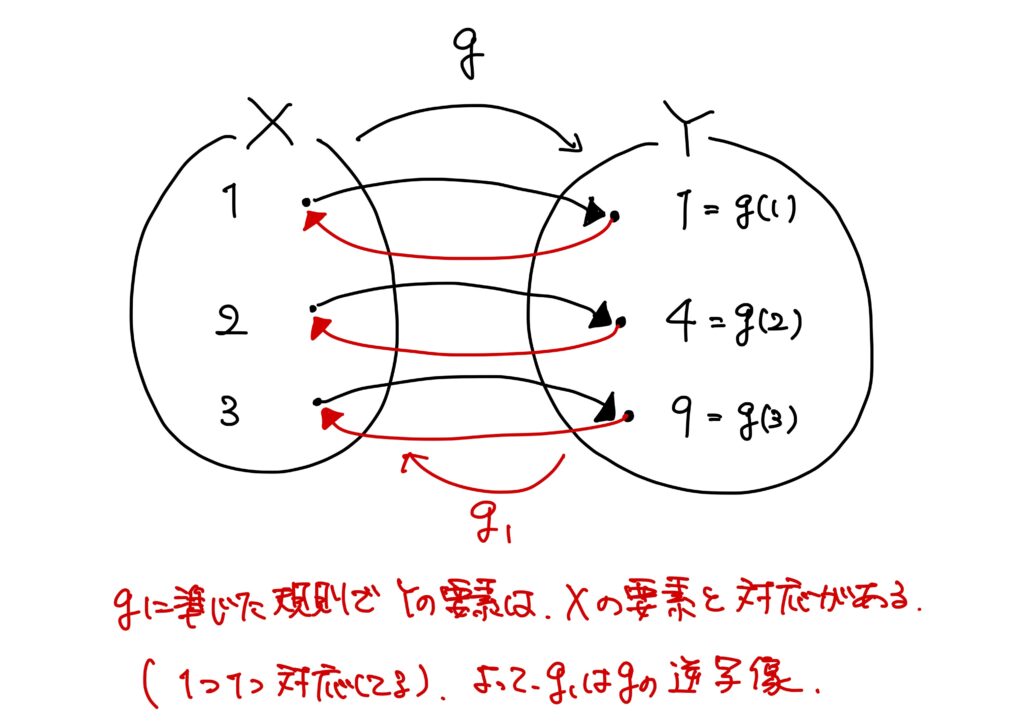
例2.
\(X=\{1,2,3\}\)、\(Y=\{1,4,9\}\)とする。
写像\(g:X\to Y\)を
- \(g(1)=1\)、
- \(g(2)=4\)、
- \(g(3)=9\)。
で定める。
また、\(g_1:Y\to X\)を
- \(g_1(1)=1\)、
- \(g_1(4)=2\)、
- \(g_1(9)=3\)。
として定める。
このとき、
- \((g_1\circ g)(1)=g_1(g(1))=g_1(1)=1\),
- \((g_1\circ g)(2)=g_1(g(2))=g_1(4)=2\),
- \((g_1\circ g)(3)=g_1(g(3))=g_1(9)=3\),
- \((g\circ g_1)(1)=g(g_1(1))=g(1)=1\),
- \((g\circ g_1)(4)=g(g_1(4))=g(2)=4\),
- \((g\circ g_1)(9)=g(g_1(9))=g(3)=9\),
であるから、\(g\circ g_1={\rm id}_X\)かつ\(g_1\circ g={\rm id}_Y\)が成り立つため、\(g_1\)は\(g\)の逆写像である。
さて、全単射の節で「逆写像が存在するのは全単射のときに限る!」という話をした。
これを証明しよう。
実はこの逆、すなわち逆写像があれば全単射である、も成り立つ。
すなわち、次が成り立つ。
(証明)
\(f:X\to Y\)を写像とする。
①「写像\(f\)が全単射ならば、\(f\)の逆写像が存在する。」ことの証明
\(f\)が全単射であるとすると\(f\)は全射であるから、任意の\(y\in Y\)に対して、ある\(x\in X\)が存在して、\(y=f(x)\)が成り立つ。
この\(x\)は一意的に、すなわちダブり無く定まる。
実際、\(x’\in X\)に対して、\(y=f(x’)\)とすると、
$$f(x)=y=f(x’)$$
である。
ここで、\(f\)は単射でもあるから、\(x=x’\)である。
従って、ダブリが無いので\(g(y)=x\)として、写像\(g:Y\to X\)を定めることができる(ダブリがあったら写像ではなくなってしまう)。
このとき、
$$(g\circ f)(x)=g(f(x))=g(y)=x$$
であり、かつ
$$(f\circ g)(y)=f(g(y))=f(x)=y$$
が成り立つ。
従って、\(g\circ f={\rm id}_X\)かつ\(f\circ g={\rm id}_Y\)が成り立つため、\(g\)は\(f\)の逆写像である。
②「写像\(f\)に逆写像が存在するならば、\(f\)は全単射である。」ことの証明
まず、恒等写像\({\rm id}_X:X\to X\)は全単射である。
実際、任意の\(x_1,x_2\in X\)に対して、\(f(x_1)=f(x_2)\)であるとすると、\(f(x_1)=x_1\)かつ\(f(x_2)=x_2\)であるため、\(x_1=x_2\)である。
従って、恒等写像は単射である。
また、任意の\(x_3\in X\)に対して、ある\(x\in X\)が存在して、\(x_3=f(x)\)であれば全射なのだが、\(x\)として\(x_3\)自身を取れば良い。
従って、恒等写像は全単射である。
\(g:Y\to X\)を\(f:\to Y\)の逆写像とする。
すなわち、
$$g\circ f={\rm id}_Xかつf\circ g={\rm id}_Y$$
が成り立つとする。
このとき、\(f\)が全単射であれば良い。
- 単射
\(f(x_1)=f(x_2)\ (x_2,x_2\in X)\)とする。
このとき、\(g\circ f={\rm id}_X\)なのだから、
$$x_1=(g\circ f)(x_1)=g(f(x_1))=g(f(x_2))=(g\circ f)(x_2)=x_2$$
となり、\(x_1=x_2\)であるから単射である。 - 全射
$$(\forall y\in Y)(\exists x\in X)\ {\rm s.t.}\ y=f(x)$$
が成り立てば良い。
つまり、上記のような\(x\in X\)を見つけてくれば良い。
\(f\circ g\)が全単射であるので、\(f\circ g\)は全射なのだから、任意の\(y\in Y\)に対して、ある\(y’\in Y\)が存在して、\(y=(f\circ g)(y’)=f(g(y’))\)を満たす。
\(x\)として\(g(y’)\)を採用すれば、\(g(y’)\in X\)であり、
$$f(x)=f(g(y’))=(f\circ g)(y’)=y$$
が成り立つ。
ここで、\(y\in Y\)は任意だったので、
$$(\forall y\in Y)(\exists x\in X)\ {\rm s.t.}\ y=f(x)$$
が成り立ったことになる。
したがって、\(f\)は全射である。
故に\(f\)は全単射である。
以上のことから、\(f\)が全単射であることと、\(f\)の逆写像が存在することは同値である。
(Q.E.D.)
逆写像は全単射のときにしか存在しないってことは逆写像って殆ど無いんじゃね?
そんなことはない。
今の議論から、「全単射でなければ逆写像も存在しないわけなのだから、\(f(x)=\sin x\)には逆写像が存在しないってことじゃんね?だって、\(f(x)=\sin x\)は全単射じゃないんだもん。」となるかもしれない。
正直なところ、半分正解で半分間違いである。
前回の記事で、
「これはどこからどこへの写像でどういうことを満たすんだろうか?」ということがわからなければ、命題の真意を汲み取ることはできない。
と述べたことがここで効いてくる。
答えを言ってしまえば、「定義域と終域によっては全単射なので逆写像が存在する。」である。
普通、\(f(x)=\sin x\)と言われたらば、「\(f:\mathbb{R}\to \mathbb{R}\)を\(f(x)=\sin x\)で定めた関数ね。」と思うだろう。
少なくとも筆者はそう思う。
高校数学でやったとおり、\(f(x)=\sin x\)は下図のようなグラフである。
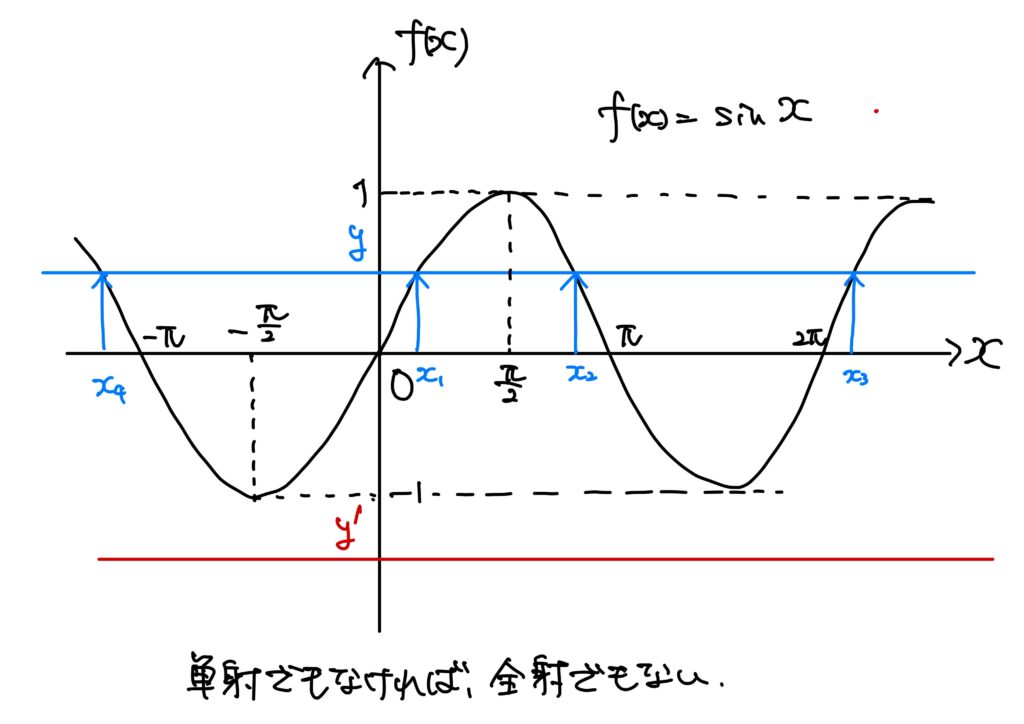
このグラフを見て直ちに「こりゃ全単射じゃねえな。単射でもなければ全射でもねえな。」と分かってくれると嬉しい。
しかし、定義域と終域を次のように絞ってみよう。
- 定義域を\(\mathbb{R}\)から\(\displaystyle\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\)に、
- 終域を\(\mathbb{R}\)から\([-1,1]\)に絞る
このように、することで、次のようなグラフになる。

このグラフを見て直ちに「全単射じゃーん」となってくれれば嬉しい。
実際全単射である。
従って、このときは逆写像が存在する。
まとめると、
- \(f:\mathbb{R}\to \mathbb{R}\)を\(f(x)=\sin x\)で定めたとき、\(f\)に逆写像(逆関数)は存在しない。
- \(\displaystyle g:\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\to [-1,1]\)を\(g(x)=\sin x\)で定めたときには逆写像\(g^{-1}\)が存在する。
この\(g^{-1}\)こそが\({\rm arcsin}\)なのである(正弦関数の逆関数)。

何が言いたかったか、というと、全単射でない写像だったとしても、定義域と終域を適切に狭めたり広げたりすることで全単射が作れる場合があるので、その場合は逆写像が存在する、ということである。
ただ、この例において、\(f\)と\(g\)は定義域の要素をどう終域の要素に対応させるか、という対応のさせ方は同じなのだが、定義域と終域が相異なるため、写像としては異なる写像である。
余談その2(逆写像の有用性)
つらつらと逆写像について語ったが、筆者が思う逆写像の有用性をもう一つ述べておく。
それは「逆写像を使うことによって、考えにくい集合から考えやすい集合に写し、考えやすい集合で考えた後、もとの集合に戻す。」という操作が逆写像によって可能になる。
「は?」と思うかもしれないので、少々記号を使って表す。
集合\(X\)である対象を考えていたとする。
大体の場合は要素が複雑な集合である。
故に、演算を決めたりなんだりと面倒なことがある。
しかし、ここで、この\(X\)が\(\mathbb{R}\)と全単射\(f:X\to \mathbb{R}\)があったとしよう。
故に、\(X\)の要素は写像\(f\)によって全て\(\mathbb{R}\)の要素とただ一つ対応している。
従って、\(X\)では複雑で面倒だったのだが、この全単射\(f\)のおかげで、\(\mathbb{R}\)で\(f(x)\ (x\in \mathbb{R})\)を考えることができる。
つまり、実質的に実数でのお話をすれば良い、ということになる。
さらに、\(f\)は全単射なので、\(f\)の逆写像が存在する。
故に、\(\mathbb{R}\)で\(f(x)\ (x\in \mathbb{R})\)を考えた後、\(f^{-1}\)で\(X\)の要素に戻す(もとに戻す)事ができる。
従って、全単射があるおかげで、より考えやすい集合で議論をし、議論が終わった後、逆写像で元に戻すことで間接的に、より容易に議論が可能だ、ということなのである。
(筆者はむしろこの使い方で逆写像を用いる。誠に平たく言えば、多様体はこのように議論をする。)
結
今回は「逆写像」について解説した。
平たく言えば、「\(f(x)\)を\(x\)に戻すような写像」のことである。
次回は解析学に戻り、「数列の発散」について解説する。
収束については述べたのだが、発散については述べていなかったので、それを述べる。
数列の発散のあとは、「関数に対する収束」について説明する。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに、「集合・写像・論理ー数学の基本を学ぶ」の方が入門者にはオススメです!





コメントをする