「行基本変形とランク〜実際にランクを求めるときに使う方法〜」【線型代数学の基礎シリーズ】行列編その8

本記事の内容
ランクのチャラい復習
行基本変形と基本行列
階段行列
階段行列とランク
1. 行基本変形をしてもランクは変わりません。
2. 行基本変形で行列のランクを計算することができる。
結

本記事の内容

本記事は行基本変形とランクについて解説する記事です。

本記事を読むにあたり、ランクについて知っている必要があるため、以下の記事も合わせてご覧ください。

ランクのチャラい復習

行列のランクについてチャラく復習します。
ランクの定め方は主に2つありました。
それは像空間の次元として定める方法と小行列の行列式で定める方法でした。

ランク(像空間の次元)

$m,n\in\mathbb{N}$ 、

$A=\left( a_{ij}\right)$ を

$(m,n)$ 型の行列とする。このとき、

$A$ が定める線型写像

$A:\mathbb{R}^n\to\mathbb{R}^m$ の像空間

${\rm Image}(A)$ の次元のことを

$A$ のランク(rank)、あるいは階数といい、

${\rm rank}(A)$ で表す。すなわち、

${\rm rank}(A)=\dim\left( {\rm Image}(A)\right)$ である。

小行列

$m,n\in\mathbb{N}$ とし、

$A=\left( a_{ij}\right)$ を

$(m,n)$ 型の行列とする。このとき、第

$i_1,i_2,\dots,i_r$ 行

$(i_1<i_2<\dots<i_r)$ と第

$j_1,j_2,\dots,j_s$ 行

$(j_1<j_2<\dots<j_s)$ の交わるところにある成分、すなわち

$\begin{eqnarray} && \begin{array}{c} &&\qquad\qquad j_1&&\quad\ j_2&\cdots&\ \ j_s&&\\ &&\qquad\qquad ↓&&\quad\ ↓&&\ \ ↓&&\\ \end{array}\\ && \begin{pmatrix} a_{11}&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&a_{1n}\\ &&\bigcirc&&\bigcirc&&\bigcirc&&\\ \vdots&&\bigcirc&&\bigcirc&&\bigcirc&&\vdots\\ \vdots&&\vdots&&\vdots&&\vdots&&\vdots\\ &&\bigcirc&&\bigcirc&&\bigcirc&&\\ a_{m1}&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&a_{mn}\\ \end{pmatrix} \begin{array}{c} \\ \leftarrow i_1行目\\ \leftarrow i_2行目\\ \vdots\\ \leftarrow i_r行目\\ \\ \end{array} \end{eqnarray}$ を取り出して作った

$(r,s)$ 型の行列

$\begin{pmatrix} a_{i_1j_1}&a_{i_1j_2}&\cdots &a_{i_1j_s}\\ a_{i_2i_1}&a_{i_2j_2}&\cdots &a_{i_2j_s}\\ \vdots&\vdots& \ddots&\vdots\\ a_{i_rj_1}&a_{i_rj_2}&\cdots &a_{i_rj_n}\\ \end{pmatrix}$ を

$A \left( \begin{array}{c} i_1&i_2&\cdots&i_r\\ j_1&j_2&\cdots&j_r\\ \end{array} \right)$ で表し、

$A$ の小行列という。特に、

$r=s$ のとき、これを

$A$ の $r$ 次の小行列という。その時の行列式

$\left| A \left( \begin{array}{c} i_1&i_2&\cdots&i_r\\ j_1&j_2&\cdots&j_r\\ \end{array} \right) \right|$ を

$A$ の $r$ 次の小行列式という。

ランク(小行列によるランク)

行列

$A$ において、

$r$ 次の小行列式の中には

$0$ でないものがあり、

$r+1$ 以上の小行列式はすべて

$0$ であるとき、この

$r$ を

$A$ のランクといい、

${\rm rank}(A)$ で表す。
ただし、零行列

$O$ のランクは

$0$ と定める。

そして、性質として以下が成り立つのでした。

定理1.

$(m,n)$ 型行列

$A$ において、次の1.〜5.の数は一致する。

$r={\rm rank}(A)$
$A$ の列ベクトル(項数が $m$ 個のベクトル)の中から選びうる線型独立なベクトルの最大個数 $s$
行列 $A$ の $t$ 次の小行列式の中には $0$ でないものがあり、 $t+1$ 次以上の小行列式はすべて $0$ である。
$A$ の行ベクトル(項数が $n$ 個のベクトル)の中から選びうる線型独立なベクトルの最大個数 $u$
$A$ の行ベクトルが生成する $\mathbb{R}^n$ の部分空間の次元 $v$

定理1.の証明は【線型代数学の基礎シリーズ】行列編その6を御覧ください。

これを見ると、「へえ。ランクを求めるには色々アプローチがあるんだあ」と思うかもしれませんが、どのアプローチでも面倒くさいのが現状だと思います(少なくとも筆者は「めんどくせぇな」と思います)。

勿論、定理1.のアプローチでランクは求まるわけですが、実は、行基本変形を行うことによってランクを求めることができます。
むしろ、通常ランクを求める際は行基本変形でもって求めます。

とどのつまり、ランクを求める際に「線型独立なベクトルの個数は〜」だの「小行列は〜」だのを考えなくて良くて、単に行列の成分に対する四則演算を数回(行列に依存します)行うだけで求まるということです。
これは相当楽ちんです。

では、前回行基本変形とは何か、という話はしましたが、再度明示します。

行基本変形と基本行列

行基本変形と列基本変形をあわせて基本変形といいます。

では、まず行基本変形について復習します。

行基本変形

行列の行基本変形

行列の次の３つの変形を行基本変形という。

(Ⅰ)１つの行に $0$ 出ない数をかける。
(Ⅱ)１つの行にある数をかけたものを他の行に加える。
(Ⅲ)２つの行を入れ替える。

これはまさに行列式を計算するときに使っていました。

基本行列

次に基本行列について解説します。
とは言っても”基本”行列というのは、まさに読んで字の如しといった具合で、基本的な形をしている行列のことを指します。

基本行列

次の3つの正方行列を基本行列という。

基本行列(Ⅰ)：単位行列の $(i,i)$ 成分が $c\neq0$ であるような行列。

$\begin{eqnarray} && \begin{array}{c} &&\qquad\quad i列目\\ &&\qquad\quad ↓\\ \end{array}\\ && \begin{pmatrix} 1&&&&\huge{O}\\ &\ddots&&&\\ &&c&&\\ &&&\ddots&\\ \huge{O}&&&&1 \end{pmatrix} \begin{array}{c} \\ \\ \leftarrow i行目\\ \\ \\ \end{array} \quad(c\neq0) \end{eqnarray}$

$c=1$

基本行列(Ⅱ)：単位行列の $(i,j)$ 成分の $0$ を $c$ で置き換えた行列

$\begin{eqnarray} && \begin{array}{c} &&\qquad\quad i列目&j列目\\ &&\qquad\quad ↓&↓\\ \end{array}\\ && \begin{pmatrix} 1&&&&&&\huge{O}\\ &\ddots&&&&&\\ &&1&&&&\\ &&\vdots&\ddots&&&\\ &&c&\cdots&1&&\\ &&&&&\ddots&\\ \huge{O}&&&&&&1 \end{pmatrix} \begin{array}{c} \\ \leftarrow i行目\\ \\ \leftarrow j行目\\ \\ \end{array}\quad(i<j),\\ && \begin{array}{c} &&\qquad\quad j列目&i列目\\ &&\qquad\quad ↓&↓\\ \end{array}\\ && \begin{pmatrix} 1&&&&&&\huge{O}\\ &\ddots&&&&&\\ &&1&\cdots&c&&\\ &&&\ddots&\vdots&&\\ &&&&1&&\\ &&&&&\ddots&\\ \huge{O}&&&&&&1 \end{pmatrix} \begin{array}{c} \\ \leftarrow j行目\\ \\ \leftarrow i行目\\ \\ \end{array}\quad(i>j) \end{eqnarray}$

基本行列(Ⅲ)：単位行列の $(i,j)$ 成分の $0$ を $c$ で置き換えた行列

$\begin{eqnarray} &&\begin{array}{c} &&&\qquad\quad\ i列目&j列目\\ &&&\qquad\quad\ ↓&↓\\ \end{array}\\ && \begin{pmatrix} 1&&&&&&&\huge{O}\\ &\ddots&&&&&&\\ &&1&&&&&\\ &&&0&\cdots&1&&\\ &&&\vdots&&\vdots&&\\ &&&1&\cdots&0&&\\ &&&&&&1&\\ &&&&&&&\ddots\\ \huge{O}&&&&&&&&1 \end{pmatrix} \begin{array}{c} \\ \leftarrow i行目\\ \\ \leftarrow j行目\\ \\ \end{array} \end{eqnarray}$

余談(まじで読まなくてOK)

行列を

$\LaTeX$ で書くのは結構面倒くさいんですよね。

$\LaTeX$ を使ったことがある方はおわかりかと思いますけど….
私の場合は

$\LaTeX$ はレポートの提出やら卒論やら修論のときに実践で鍛えられましたが、でもやっぱり大変なものは大変なんですよねえ。

行基本変形と基本行列の関係

実は、行列の行基本変形のというのは、ある行列に基本行列をかけるという操作を指しています。
「ホントかな？」と思うかもしれませんが、実際に計算してみると分かります。

定理2.

基本行列は正則であり、行基本変形は基本行列を左からかけるという操作によって得られる。従って、基本変形はある正則行列を左からかける操作によって得られる。

定理2.の証明

なんてことありません。

基本行列が正則行列であることを示すには、これらの行列式が $0$ でないことを証明すればOKです。
なぜならば、行列式が $0$ でないことと正則であることは同値だからです。
すなわち、次が成り立っていたからです。

定理3.

正方行列

$A$ が正則であるための必要十分条件は、

$\det(A)\neq0$ である。このとき、

$A$ の逆行列

$A^{-1}$ は

$A^{-1}=\frac{1}{\det(A)}\tilde{A}$ であたえられる。ただし、

$\tilde{A}$ は

$A$ の余因子行列である。

定理3.の証明は【線型代数学の基礎シリーズ】行列式編その6を御覧ください。

まず、(Ⅰ)の行列式は、対角成分の積と等しいので、 $c\neq0$ です。
次に(Ⅱ)のはそれぞれ下三角行列、上三角行列ですので、これも行列式は対角成分と等しいから $1\neq0$ です。
最後に(Ⅲ)ですが、これは行基本変形を行うことで $-1\neq0$ だと分かります。
従って、基本行列は正則です。

行列 $A$ の左から(Ⅰ)、(Ⅱ)、(Ⅲ)をかけることは、それぞれ

(Ⅰ)： $A$ の第 $i$ 行を $c$ 倍する。(行基本変形(Ⅰ))
(Ⅱ)： $A$ の第 $i$ 行を $c$ 倍して、第 $j$ 行に加える。(行基本変形(Ⅱ))
(Ⅲ)： $A$ の第 $i$ 行と第 $j$ 行を入れ替える。(行基本変形(Ⅲ))

ということに対応します。
従って、行基本変形はある正則行列を左からかける事により得られます。

定理2.の証明終わり

基本行列が正則だということが分かったので、基本行列の逆行列を具体的に与えます。

定理4.

基本行列(Ⅰ)、(Ⅱ)、(Ⅲ)の逆行列(Ⅰ)’、(Ⅱ)’、(Ⅲ)’は次で与えられる。

基本行列(Ⅰ)の逆行列(Ⅰ)’

$\begin{eqnarray} && \begin{array}{c} &&\qquad\quad\qquad\quad i列目\\ &&\qquad\quad\qquad\quad ↓\\ \end{array}\\ && (Ⅰ)’=\begin{pmatrix} 1&&&&\huge{O}\\ &\ddots&&&\\ &&c^{-1}&&\\ &&&\ddots&\\ \huge{O}&&&&1 \end{pmatrix} \begin{array}{c} \\ \\ \leftarrow i行目\\ \\ \\ \end{array} \quad(c\neq0) \end{eqnarray}$

$c=1$

基本行列(Ⅱ)の逆行列(Ⅱ)’

$\begin{eqnarray} && \begin{array}{c} &&\qquad\quad\qquad\quad i列目&\quad j列目\\ &&\qquad\quad\qquad\quad ↓&↓\\ \end{array}\\ && (Ⅱ)’_1=\begin{pmatrix} 1&&&&&&\huge{O}\\ &\ddots&&&&&\\ &&1&&&&\\ &&\vdots&\ddots&&&\\ &&-c&\cdots&1&&\\ &&&&&\ddots&\\ \huge{O}&&&&&&1 \end{pmatrix} \begin{array}{c} \\ \leftarrow i行目\\ \\ \leftarrow j行目\\ \\ \end{array}\quad(i<j),\\ && \begin{array}{c} &&\qquad\quad\qquad\quad j列目&\quad i列目\\ &&\qquad\quad\qquad\quad ↓&\quad↓\\ \end{array}\\ && (Ⅱ)’_2=\begin{pmatrix} 1&&&&&&\huge{O}\\ &\ddots&&&&&\\ &&1&\cdots&-c&&\\ &&&\ddots&\vdots&&\\ &&&&1&&\\ &&&&&\ddots&\\ \huge{O}&&&&&&1 \end{pmatrix} \begin{array}{c} \\ \leftarrow j行目\\ \\ \leftarrow i行目\\ \\ \end{array}\quad(i>j) \end{eqnarray}$

基本行列(Ⅲ)の逆行列(Ⅲ)’

$\begin{eqnarray} &&\begin{array}{c} &&&\qquad\quad\qquad\quad\quad i列目&j列目\\ &&&\qquad\quad\qquad\quad\quad↓&↓\\ \end{array}\\ && (Ⅲ)’=\begin{pmatrix} 1&&&&&&&\huge{O}\\ &\ddots&&&&&&\\ &&1&&&&&\\ &&&0&\cdots&1&&\\ &&&\vdots&&\vdots&&\\ &&&1&\cdots&0&&\\ &&&&&&1&\\ &&&&&&&\ddots\\ \huge{O}&&&&&&&&1 \end{pmatrix} \begin{array}{c} \\ \leftarrow i行目\\ \\ \leftarrow j行目\\ \\ \end{array} \end{eqnarray}$

列基本変形

行基本変形とほぼ同じなのでサラッと行きます。

行列の行基本変形

行列の次の３つの変形を列基本変形という。

(Ⅰ)１つの列に $0$ でない数をかける。
(Ⅱ)１つの列にある数をかけたものを他の列に加える。
(Ⅲ)２つの列を入れ替える。

定理5.

列基本変形は、以前の基本行列を右から欠けるという操作によって得られる。

あ定理5.の証明も定理2.の証明の「行」を「列」に変えて、「左」を「右」に変えるだけですので省略します。

階段行列

先程までは、前回の連立一次方程式を解くための手法の基本変形を抽象化して行列の行基本変形について考えました。
この行列の行基本変形の手法は連立一次方程式の解法だけではなく、行列のランクを求めたり、正則行列の場合はその逆行列を具体的に計算するのに便利です(この記事では逆行列の求め方は書きません)。

従って行基本変形というのは誠に有用です。
しかし、与えられた行列に対して無闇矢鱈に変形するのではなくて、ある形を目標として、それに向かって基本変形をすることが大切です。
その目標こそが階段行列なのです。

階段行列って何スか？

ひとことで言うと、

行の番号が増えるに従って、左側に連続して並ぶ

$0$ の個数が増えていく(まさに階段)ような行列のこと。

です。

これをしっかり書くと次です。

階段行列

行番号が増えるにつれて、左側に連続して並ぶ $0$ の個数が増えていくような行列を階段行列という。各行において、左から連続して並ぶ $0$ と最初に $0$ でない数が出るところの境目に着目すると、次のような階段が得られる。

ｓ任意の行列は行基本変形を繰り返すことで階段行列になる。

そうなんです。凄いよね。

定理6.

任意の行列は行基本変形を繰り返すことで階段行列に変形することができる。

定理6.の証明

$A=\begin{pmatrix} a_{11}&\cdots &a_{1n}\\ \vdots& \ddots&\vdots\\ a_{m1}&\cdots &a_{mn}\\ \end{pmatrix}$
を与えられた行列とします。
このとき、第１列の成分の $a_{11},\dots,a_{m1}$ の中に $0$ でないものがあるとき、その１つを取ります。
例えば、 $a_{i1}\neq0$ だとします。
第１行と第 $i$ 行を入れ替える(行基本変形(Ⅲ))ことで、新たに $(1,1)$ 成分が $0$ でなくなるので、 $a_{11}\neq0$ とします。
このとき、 $2$ 以上の各 $i$ に対して、

(第

$i$ 行)

$+$ (第

$1$ 行)

$\displaystyle\times\frac{-a_{i1}}{a_{11}}$

という行基本変形(Ⅱ)を行うことで、
$\left( \begin{array}{c|ccc} a_{11}&a_{12}&\cdots &a_{1n}\\ \hline 0&&&\\ \vdots&&\huge{B}&\\ 0&&&\\ \end{array} \right)$
の形に変形することができます。
また、第１列の成分がすべて $0$ であれば、そのままで
$\left( \begin{array}{c|cc} 0&&\\ \vdots&\huge{B}&\\ 0&&\\ \end{array} \right)$
の形です。

次に、この行列 $B$ について、 $B$ の第１列に対して同じ操作を行います。
この操作を繰り返していくと、段々 $B$ が右下の方向に小さくなります。
最終的には、この操作で階段行列が得られ、かつ有限回の操作で終了します。

定理6.の証明終わり

定理2.から、基本変形はある正則な行列をかけるという操作に対応するのでした。

定理7.

任意の行列は、適当な正則行列を左からかけることによって階段行列にすることができる。

定理7.の証明

定理6.から任意の行列は行基本変形によって階段行列に変形されます。
また、定理2.からこの行基本費ぇん系はある正則行列を左からかけるという操作によって得られ、また、正則行列の積は正則行列ですので、証明完了です。

定理7.の証明終わり

いっちょ計算してみっか

してみましょ。

例8.
$\begin{pmatrix} 0&1 &-1&2\\ 1&-2&3&9\\ 4&2&2&0\\ \end{pmatrix}$
を階段行列に変形してみます。
$\begin{eqnarray} &&\begin{pmatrix} 0&1 &-1&2\\ 1&-2&3&9\\ 4&2&2&0\\ \end{pmatrix}\xrightarrow{(Ⅲ)} \begin{pmatrix} 1&-2&3&9\\ 0&1&-1&2\\ 4&2&2&0\\ \end{pmatrix}\\ && \xrightarrow{(Ⅱ)} \begin{pmatrix} 1&-2&3&9\\ 0&1&-1&2\\ 0&10&-10&-36\\ \end{pmatrix} \xrightarrow{(Ⅱ)} \begin{pmatrix} 1&-2&3&9\\ 0&1&-1&2\\ 0&0&0&-56\\ \end{pmatrix} \end{eqnarray}$
はじめに第１行と第２行を入れ替えて、次に第３行に(第1行) $\times(-4)$ を加えます。
そして、第3行に(第２行) $\times(-10)$ を加えます。
おしまい。

階段行列とランク

行基本変形をしてもランクは変わりません。

定理9.

行基本変形により、行列のランクは不変である。

定理9.の証明

行列 $A$ に行基本変形を何回か行って、行列 $B$ に移ったとしましょう。
定理2.から正則行列 $P$ が存在して、
$PA=B$
が成り立ちます。
ここで、行列の積に対するランクを考えてみます。

定理10.

$(m,n)$ 型行列 $A$ と $(n,l)$ 型行列 $B$ について、以下が成り立つ。
${\rm rank}(AB)\leq \min\left\{{\rm rank}(A),{\rm rank}(B)\right\}$

定理10.の証明

行列 $A$ 、 $B$ を線型写像
$A: \mathbb{R}^n\to\mathbb{R}^m,\quad B:\mathbb{R}^l\to\mathbb{R}^n$
ととらえると、この２つの線型写像の合成写像は行列の積
$AB: \mathbb{R}^l\to\mathbb{R}^m$
で与えられます。
ここで、
$B(\mathbb{R}^l)={\rm Image}(B)\subset\mathbb{R}^n$
ですので、
${\rm Image}(AB)=AB(\mathbb{R}^l)\subset A(\mathbb{R}^n)={\rm Image}(A)$
となります。

従って、
${\rm rank}(AB)=\dim\left( {\rm Image}(AB)\right)\leq\dim\left( {\rm Image}(A)\right)={\rm rank}(A)$
となります。

ここで、次の事実を使います。

定理11.

$(m,n)$ 型行列 $A$ において、次の1.〜5.の数は一致する。

$r={\rm rank}(A)$
$A$ の列ベクトル(項数が $m$ 個のベクトル)の中から選びうる線型独立なベクトルの最大個数 $s$
行列 $A$ の $t$ 次の小行列式の中には $0$ でないものがあり、 $t+1$ 次以上の小行列式はすべて $0$ である。
$A$ の行ベクトル(項数が $n$ 個のベクトル)の中から選びうる線型独立なベクトルの最大個数 $u$
$A$ の行ベクトルが生成する $\mathbb{R}^n$ の部分空間の次元 $v$

定理11.の証明は【線型代数学の基礎シリーズ】行列編その6を御覧ください。

定理11.から、一般に行列 $X$ のランクと $X^\top$ のランクが一致するので、
${\rm rank}(AB)={\rm rank}\left( (AB)^\top\right)={\rm rank}(B^\top A^\top)\leq {\rm rank}(B^\top)={\rm rank}(B)$
となります。
従って、２つの不等式から
${\rm rank}(AB)\leq \min\left\{{\rm rank}(A),{\rm rank}(B)\right\}$
です。

定理10.の証明終わり

定理12.

$A$ を $(m,n)$ 型の行列、 $B$ を $m$ 次の正則行列、 $C$ を $n$ 次の正則行列とするとき、
${\rm rank}(BAC)={\rm rank}(BA)={\rm rank}(AC)={\rm rank}(A)$
である。

定理12.の証明

定理10.から、
$\begin{eqnarray} &&{\rm rank}(BAC)\leq {\rm rank}(BA)\leq {\rm rank}(A)\\ {\rm rank}(BAC)\leq {\rm rank}(AC)\leq {\rm rank}(A) \end{eqnarray}$
が成り立ちます。
家庭から、 $B$ と $C$ は正則行列ですので、それぞれの逆行列 $B^{-1}$ 、 $C^{-1}$ が存在します。
従って、
$\begin{eqnarray} {\rm rank}(A)&=&{\rm rank}\left((BB^{-1})A(CC^{-1}) \right)={\rm rank}\left( B^{-1}(BAC)C^{-1}\right)\\ &\leq&{\rm rank}(BAC)C^{-1}\leq {\rm rank}(BAC) \end{eqnarray}$
となります。
従って、前半の不等式と合わせることで、これらはすべて等しいことが分かります。

定理12.の証明終わり

さて、定理9.の証明に戻ります。
今、正則行列 $P$ を用いて
$PA=B$
なのでした。
定理12.から、
${\rm rank}(B)={\rm rank}(PA)={\rm rank}(A)$
が成り立ちます。
従って、行基本変形により、行列のランクは不変です。

定理9.の証明終わり

行基本変形で行列のランクを計算することができる。

最も言いたかったことです。
準備に時間がかかっちゃいましたが。

では行きましょう。
最後のひと押しです。

定理13.

行列 $A$ に行基本変形を行って、階段行列

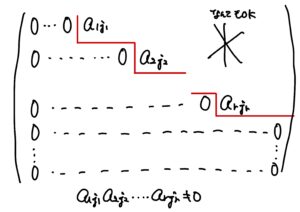
になったとすると、 ${\rm rank}(A)=r$ である。

定理13.の証明

定理9.により、行列のランクは行基本変形で不変です。
故に行列 $A$ が階段行列の場合に示せばOKです。
そこで、以降は $A$ を本定理の階段行列だとします。

行列 $A$ の行ベクトルを $\boldsymbol{a}_1,\dots,\boldsymbol{a}_m$ としましょう。
まず、 $\boldsymbol{a}_{r+1}=\dots=\boldsymbol{a}_m=0$ であり、
$\boldsymbol{a}_i=(0\ \cdots\ 0\ a_{ij_i}\ \ast\ \cdots\ \ast)\quad(a_{ij_i}\neq0)$
という形になっています。
そのとき、 $\boldsymbol{a}_1,\dots,\boldsymbol{a}_r$ が線型独立だということを示しましょう。
$\sum_{i=1}^rc_i\boldsymbol{a}_i=\boldsymbol{0}$
とします。
左辺のベクトルの線型結合の第 $j_1$ 成分に着目すると、 $j_1$ 成分が $0$ でないようなベクトルは $\boldsymbol{a}_1$ だけです(行列の図を参照)。
しかも、その成分は $c_1a_{1j_1}$ です。
仮定から $c_1a_{1j_1}=0$ で、今 $a_{1j_1}\neq0$ なのですから、 $c_1=0$ です。
結果として
$\sum_{i=1}^rc_i\boldsymbol{a}_i=\sum_{i=2}^rc_i\boldsymbol{a}_i=\boldsymbol{0}$
となりますが、全くもって同様の理由で $c_2=0$ が導けます。
故に、 $c_i=0$ が示されるので、 $\boldsymbol{a}_1,\dots,\boldsymbol{a}_r$ は線型独立です。

一方で、その他のベクトル $\boldsymbol{a}_{r+1},\dots,\boldsymbol{a}_m$ はすべて零ベクトルなので、 $A$ の行ベクトルの中から選びうる線型独立なベクトルの最大数はまさに $r$ 個です。
従って、定理11.から $r={\rm rank}(A)$ です。

定理13.の証明終わり

ということで、行列のランクを求めるには行基本変形をすることで求めるのが良い、ということです。
実は列基本変形でも同じことが言えます。
故に同時に使ってOKです。
しかしながら、筆者の体感だと、行基本変形だけ、列基本変形だけ、というようにいずれか一方のほうが早く計算が終わると思います。
というのも、ランクを求めるにあたって、目標は階段行列にすることなのであって、単位行列のように対角成分が1で他が $0$ になるまで計算する必要が無いからです。

結

今回は行基本変形とランクについて解説しました。
ランクは像空間の次元と小行列式でもって定めましたが、いざ計算するとなると面倒です。
実は、行基本変形と列基本変形を駆使して階段行列に変形することで簡単にランクが求まります。

次回は線型代数の中でも誠に重要な「固有値、固有ベクトル」について解説します。

乞うご期待！質問、コメントなどお待ちしております！

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34