「余因子、余因子展開、余因子行列」【線型代数学の基礎シリーズ】行列式編 その5

本記事の内容

本記事は余因子、余因子展開と余因子行列について解説する記事です。
本記事を読むにあたり、行列式について知っている必要があるため、以下の記事も合わせてご覧ください。

「行列式とその性質①」【線型代数学の基礎シリーズ】行列式編 その2

...

for-spring.com

2022.07.06

本記事で言いたいこと

本記事で言いたいことは、

ということです。
ポップに書きましたが、ちゃんと書きますので、ご安心を。

余因子展開をサラッというと、

を指します。

ここで「んぉ？これ、前に似たようなことやらなかったか？」と思った方、鋭いです。
以前、行列式の性質として以下の性質を証明しました。

この定理1.の証明は【線型代数学の基礎シリーズ】行列式編 その2を御覧ください。

これは確かに$n$次正方行列の行列式を$n-1$次正方行列の行列式に帰着しています。
ただ、これは第1列が$(1,1)$成分以外の成分がすべて$0$の場合でした。

ここで、「行列の行の順序を置換$\tau$によって変更すると、行列式は${\rm sgn}(\tau)$倍になる。」という性質を思い出してみます。

この定理2.の証明は【線型代数学の基礎シリーズ】行列式編 その3を御覧ください。

さて、この定理2.と定理1.によって
$$\begin{eqnarray} \left| \begin{array}{c} 0&a_{12}&\cdots &a_{1n}\\ 0&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& &\vdots\\ a_{i1}&a_{i_2}& \cdots&a_{in}\\ \vdots&\vdots& &\vdots\\ 0&a_{n2}&\cdots &a_{nn}\\ \end{array}\right|&=& -\left| \begin{array}{c} a_{i1}&a_{i_2}& \cdots&a_{in}\\ 0&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& &\vdots\\ 0&a_{12}&\cdots &a_{1n}\\ \vdots&\vdots& &\vdots\\ 0&a_{n2}&\cdots &a_{nn}\\ \end{array}\right|\\ &=& -a_{i1}\left| \begin{array}{c} a_{22}&\cdots &a_{2n}\\ \vdots& &\vdots\\ a_{12}&\cdots &a_{1n}\\ \vdots& &\vdots\\ a_{n2}&\cdots &a_{nn}\\ \end{array}\right|\\ \end{eqnarray}$$
が成り立ちます。
従って、「第1列の$(1,1)$成分以外が$0$」という条件を弱めた主張が得られます。
つまり、「第1列の$(i,1)$成分以外が$0$のとき」の場合の主張が導けます。

これを更に一般化したのが余因子展開です。
つまり、「一般の行列に対して同じようなことができないかな？」ということの答えが余因子展開です。

余因子

ではまず、余因子行列について解説します。

余因子って何スか？

余因子を一言でいうと、

です。

「ﾅﾝｼﾞｬｿﾚ」となるかもしれませんので、明記してしまいます。

ここで注意なのが、余因子というのはあくまで数(複素行列なら複素数、実行列なら実数)であって、行列ではありません。
正方行列の第$i$行および第$j$列に対して定められる数です。

余因子をチャラくいうと、

ということです。

ではこの余因子を計算してみましょう。

いっちょ計算してみっか

例3.
$$A= \begin{pmatrix} 1&2&0\\ 3&5&-1\\ 4&6&7 \end{pmatrix}$$
として、$A$の余因子をいっちょ計算してみましょう。

• $a_{11}$の余因子$\tilde{a}_{11}$(第1行と第1列を抜いたとき)
  $$A_{11}=\begin{pmatrix}5&-1\\6&7\end{pmatrix},\quad \tilde{a}_{11}=(-1)^2\det(A_{11})=35+6=41$$
• $a_{12}$の余因子$\tilde{a}_{12}$(第1行と第2列を抜いたとき)
  $$A_{12}=\begin{pmatrix}3&-1\\4&7\end{pmatrix},\quad \tilde{a}_{12}=(-1)^3\det(A_{12})=-(21+4)=-25$$
• $a_{13}$の余因子$\tilde{a}_{13}$(第1行と第3列を抜いたとき)
  $$A_{13}=\begin{pmatrix}3&5\\4&6\end{pmatrix},\quad \tilde{a}_{13}=(-1)^4\det(A_{13})=18-20=-2$$
• $a_{21}$の余因子$\tilde{a}_{21}$(第2行と第1列を抜いたとき)
  $$A_{21}=\begin{pmatrix}2&0\\6&7\end{pmatrix},\quad \tilde{a}_{21}=(-1)^3\det(A_{21})=-(14-0)=-14$$
• $a_{22}$の余因子$\tilde{a}_{22}$(第2行と第2列を抜いたとき)
  $$A_{22}=\begin{pmatrix}1&0\\4&7\end{pmatrix},\quad \tilde{a}_{22}=(-1)^4\det(A_{22})=7-0=7$$
• $a_{23}$の余因子$\tilde{a}_{23}$(第2行と第3列を抜いたとき)
  $$A_{23}=\begin{pmatrix}1&2\\4&6\end{pmatrix},\quad \tilde{a}_{23}=(-1)^5\det(A_{23})=-(6-8)=2$$
• $a_{31}$の余因子$\tilde{a}_{31}$(第3行と第1列を抜いたとき)
  $$A_{31}=\begin{pmatrix}2&0\\5&-1\end{pmatrix},\quad \tilde{a}_{31}=(-1)^4\det(A_{31})=-2-0=-2$$
• $a_{32}$の余因子$\tilde{a}_{32}$(第3行と第2列を抜いたとき)
  $$A_{32}=\begin{pmatrix}1&0\\3&-1\end{pmatrix},\quad \tilde{a}_{32}=(-1)^5\det(A_{32})=-(-1)=1$$
• $a_{33}$の余因子$\tilde{a}_{33}$(第3行と第3列を抜いたとき)
  $$A_{33}=\begin{pmatrix}1&2\\3&5\end{pmatrix},\quad \tilde{a}_{33}=(-1)^6\det(A_{33})=5-6=-1$$

このように、$n$次正方行列の余因子は$n^2$個あります。

余因子展開（行編）

さて、いよいよ余因子展開の話をします。
なぜ余因子”展開”と言われるのか、ということが次の定理で分かるかと思います。

「ﾅﾝｼﾞｬﾗﾎｲ?」という具合かもしれませんので、サラッとこの定理4.の言いたいことを書き下します。

定理4.の主張をサラッと解説すると、

ということです。
これをより具体的に書いてみます。

$$\begin{eqnarray} \left|\begin{array}{c} a_{11}&\cdots&a_{1j}&\cdots &a_{1n}\\ \vdots&&\vdots&&\vdots\\ a_{i1}&\cdots&a_{ij}&\cdots&a_{in}\\ \vdots&&\vdots&&\vdots\\ a_{n1}&\cdots&a_{nj}&\cdots&a_{nn}\\ \end{array}\right|&=& (-1)^{i+1}a_{i1}\left|\begin{array}{c} a_{12}&\cdots&a_{1j}&\cdots &a_{1n}\\ \vdots&&\vdots&&\vdots\\ a_{i-1\ 2}&\cdots&a_{i-1\ j}&\cdots&a_{i-1\ n}\\ a_{i+1\ 2}&\cdots&a_{i+1\ j}&\cdots&a_{i+1\ n}\\ \vdots&&\vdots&&\vdots\\ a_{n2}&\cdots&a_{nj}&\cdots&a_{nn}\\ \end{array}\right|\\ &&+ (-1)^{i+2}a_{i2}\left|\begin{array}{c} a_{11}&a_{13}&\cdots&a_{1j}&\cdots &a_{1n}\\ \vdots&\vdots&&\vdots&&\vdots\\ a_{i-1\ 1}&a_{i-1\ 3}&\cdots&a_{i-1\ j}&\cdots&a_{i-1\ n}\\ a_{i+1\ 1}&a_{i+1\ 3}&\cdots&a_{i+1\ j}&\cdots&a_{i+1\ n}\\ \vdots&\vdots&&\vdots&&\vdots\\ a_{n1}&a_{n3}&\cdots&a_{nj}&\cdots&a_{nn}\\ \end{array}\right|\\ &&+\cdots\cdots\\ &&+(-1)^{i+j}a_{ij}\left| \begin{array}{c} a_{11}&\cdots&a_{1\ j-1}&a_{1\ j+1}&\cdots&a_{1n}\\ \vdots&&\vdots&\vdots&&\vdots\\ a_{i-1\ 1}&\cdots&a_{i-1\ j-1}&a_{i-1\ j+1}&\cdots&a_{i-1\ n}\\ a_{i+1\ 1}&\cdots&a_{i+1\ j-1}&a_{i+1\ j+1}&\cdots&a_{i+1\ n}\\ \vdots&&\vdots&\vdots&&\vdots\\ a_{n1}&\cdots&a_{n\ j-1}&a_{n\ j+1}&\cdots&a_{nn}\\ \end{array}\right|\\ &&+\cdots\cdots\\ &&+ (-1)^{i+n}a_{in} \left|\begin{array}{c} a_{11}&\cdots&a_{1j}&\cdots &a_{1\ n-1}\\ \vdots&&\vdots&&\vdots\\ a_{i-1\ 1}&\cdots&a_{i-1\ j}&\cdots&a_{i-1\ n-1}\\ a_{i+1\ 1}&\cdots&a_{i+1\ j}&\cdots&a_{i+1\ n-1}\\ \vdots&&\vdots&&\vdots\\ a_{n1}&\cdots&a_{nj}&\cdots&a_{n\ n-1}\\ \end{array}\right| \end{eqnarray}$$

ということです。
「んぉ？むしろわからん」となるかもしれませんので、図で説明します。

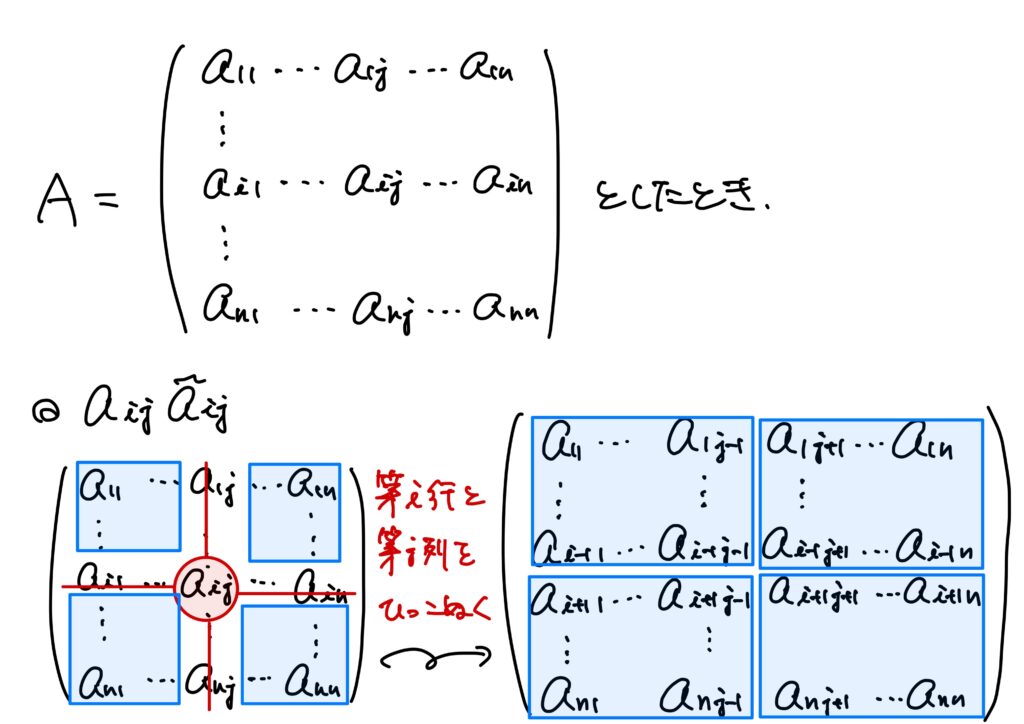
ということです。

では、証明に入りましょう！

定理4.の証明

$n\in\mathbb{N}$、$A=\left( a_{ij}\right)$を$n$次正方行列として、
$$A= \begin{pmatrix} a_{11}&\cdots&a_{1n}\\ \vdots&&\vdots\\ a_{n1}&\cdots&a_{nn}\\ \end{pmatrix}$$
と書いたとします。

(1.の証明)

$A=\left( a_{ij}\right)$の第$i$行$(a_{i1}\ \cdots\ a_{ij}\ \cdots\ a_{in})$は、
$$(a_{i1}\ \cdots\ a_{ij}\ \cdots\ a_{in})=(a_{i1}\ 0\cdots0)+(0\ a_{i2}\ 0\cdots0)+\dots+(0\ \cdots\ 0\ a_{in})$$
というように、$(i,j)$成分以外が$0$の$n$個の行ベクトルの和で書くことができます。
従って、以下の定理を使うことができます。

定理5.の証明は【線型代数学の基礎シリーズ】行列式編 その3を御覧ください。

定理5.を繰り返し使えば、
$$\begin{eqnarray} \det(A)&=& \left| \begin{array}{c} a_{11}&\cdots&\cdots&\cdots &a_{1n}\\ \vdots&&&&\vdots\\ a_{i1}&0&\cdots&\cdots&0\\ \vdots&&&&\vdots\\ a_{n1}&\cdots&\cdots&\cdots&a_{nn}\\ \end{array} \right|+ \left| \begin{array}{c} a_{11}&\cdots&\cdots&\cdots &a_{1n}\\ \vdots&&&&\vdots\\ 0&a_{i2}&0&\cdots&0\\ \vdots&&&&\vdots\\ a_{n1}&\cdots&\cdots&\cdots&a_{nn}\\ \end{array} \right|+\cdots\\ &&\cdots+ \left| \begin{array}{c} a_{11}&\cdots&\cdots&\cdots &a_{1n}\\ \vdots&&&&\vdots\\ 0&\cdots&\cdots&0&a_{in}\\ \vdots&&&&\vdots\\ a_{n1}&\cdots&\cdots&\cdots&a_{nn}\\ \end{array} \right| \end{eqnarray}$$
となります。

この右辺の$j$番目を計算してみましょう。
右辺の$j$番目は次です。
$$\left| \begin{array}{c} a_{11}&\cdots&\cdots&a_{1j} &\cdots&\cdots&a_{1n}\\ \vdots&&&\vdots&&&\vdots\\ 0&\cdots&0&a_{ij}&0&\cdots&0\\ \vdots&&&\vdots&&&\vdots\\ a_{n1}&\cdots&\cdots&a_{nj}&\cdots&\cdots&a_{nn}\\ \end{array} \right|$$

まず、この行列式の第$i$行を順に１つ上の行と入れ替える操作をして、第$i$行を第1行まで移動させます。
ここで、次の定理を思い出します。

定理6.の証明は【線型代数学の基礎シリーズ】行列式編 その3を御覧ください。

定理6.から1回の行の入れ替えの操作によって、行列式は$-1$倍になります。
故に第$i$行を第1行まで移動させるには、行の入れ替えの操作は$i-1$回行われるので、第$i$行が第1行に移動したときの行列式は$(-1)^{i-1}$倍されます。
従って、
$$\left| \begin{array}{c} a_{11}&\cdots&\cdots&a_{1j} &\cdots&\cdots&a_{1n}\\ \vdots&&&\vdots&&&\vdots\\ 0&\cdots&0&a_{ij}&0&\cdots&0\\ \vdots&&&\vdots&&&\vdots\\ a_{n1}&\cdots&\cdots&a_{nj}&\cdots&\cdots&a_{nn}\\ \end{array} \right|= (-1)^{i-1}\left| \begin{array}{c} 0&\cdots&0&a_{ij}&0&\cdots&0\\ \vdots&&&\vdots&&&\vdots\\ a_{11}&\cdots&\cdots&a_{1j} &\cdots&\cdots&a_{1n}\\ \vdots&&&\vdots&&&\vdots\\ a_{n1}&\cdots&\cdots&a_{nj}&\cdots&\cdots&a_{nn}\\ \end{array} \right|$$

次に、先ほどと同様に第$j$列を１つ左の列と入れ替える操作によって第1列まで移動させます。
このとき、次の定理を使います。

定理7.の証明は【線型代数学の基礎シリーズ】行列式編 その4を御覧ください。

定理7.から1回の列の入れ替えの操作によって、行列式は$-1$倍になります。
故に第$j$列を第1列まで移動させるには、列の入れ替えの操作は$j-1$回行われるので、第$j$列が第1列に移動したときの行列式は$(-1)^{j-1}$倍されます。
故に、

$$(-1)^{i-1}\left| \begin{array}{c} 0&\cdots&0&a_{ij}&0&\cdots&0\\ \vdots&&&\vdots&&&\vdots\\ a_{11}&\cdots&\cdots&a_{1j} &\cdots&\cdots&a_{1n}\\ \vdots&&&\vdots&&&\vdots\\ a_{n1}&\cdots&\cdots&a_{nj}&\cdots&\cdots&a_{nn}\\ \end{array} \right| \\=(-1)^{i+j-2}\left| \begin{array}{cccc|ccc} a_{ij}&0&\cdots&0&0&\cdots&0\\ a_{1j}&a_{11}&\cdots&a_{1\ j-1} &a_{1\ j+1}&\cdots&a_{1n}\\ \vdots&\vdots&&\vdots&\vdots&&\vdots\\ a_{i-1\ j}&a_{i-1\ 1}&\cdots&a_{i-1\ j-1} &a_{i-1\ j+1}&\cdots&a_{i-1\ n}\\ \hline a_{i+1\ j}&a_{i+1\ 1}&\cdots&a_{i+1\ j-1} &a_{i+1\ j+1}&\cdots&a_{i+1\ n}\\ \vdots&\vdots&&\vdots&\vdots&&\vdots\\ a_{nj}&a_{n1}&\cdots&a_{n\ j-1} &a_{n\ j+1}&\cdots&a_{nn}\\ \end{array} \right|$$
となります。

ここで、次の定理を使います。

定理8.の証明は【線型代数学の基礎シリーズ】行列式編 その4を御覧ください。

定理8.により、行列式は転置しても不変なので、
$$(-1)^{i+j-2}\left| \begin{array}{cccc|ccc} a_{ij}&0&\cdots&0&0&\cdots&0\\ a_{1j}&a_{11}&\cdots&a_{1\ j-1} &a_{1\ j+1}&\cdots&a_{1n}\\ \vdots&\vdots&&\vdots&\vdots&&\vdots\\ a_{i-1\ j}&a_{i-1\ 1}&\cdots&a_{i-1\ j-1} &a_{i-1\ j+1}&\cdots&a_{i-1\ n}\\ \hline a_{i+1\ j}&a_{i+1\ 1}&\cdots&a_{i+1\ j-1} &a_{i+1\ j+1}&\cdots&a_{i+1\ n}\\ \vdots&\vdots&&\vdots&\vdots&&\vdots\\ a_{nj}&a_{n1}&\cdots&a_{n\ j-1} &a_{n\ j+1}&\cdots&a_{nn}\\ \end{array} \right|\\ = (-1)^{i+j-2}\left| \begin{array}{cccc|ccc} a_{ij}&a_{1j}&\cdots&a_{i-1\ j}&a_{i+1\ j}&\cdots&a_{nj}\\ 0&a_{11}&\cdots&a_{i-1\ 1} &a_{i+1\ 1}&\cdots&a_{n1}\\ \vdots&\vdots&&\vdots&\vdots&&\vdots\\ 0&a_{1\ j-1}&\cdots&a_{i-1\ j-1} &a_{i+1\ j-1}&\cdots&a_{n\ j-1}\\ \hline 0&a_{1\ j+1}&\cdots&a_{i-1\ j+1} &a_{i+1\ j+1}&\cdots&a_{n\ j+1}\\ \vdots&\vdots&&\vdots&\vdots&&\vdots\\ 0&a_{1n}&\cdots&a_{i-1\ n} &a_{i+1\ n}&\cdots&a_{nn}\\ \end{array} \right|$$
となります。
ここで定理1.から、
$$(-1)^{i+j-2}\left| \begin{array}{cccc|ccc} a_{ij}&a_{1j}&\cdots&a_{i-1\ j}&a_{i+1\ j}&\cdots&a_{nj}\\ 0&a_{11}&\cdots&a_{i-1\ 1} &a_{i+1\ 1}&\cdots&a_{n1}\\ \vdots&\vdots&&\vdots&\vdots&&\vdots\\ 0&a_{1\ j-1}&\cdots&a_{i-1\ j-1} &a_{i+1\ j-1}&\cdots&a_{n\ j-1}\\ \hline 0&a_{1\ j+1}&\cdots&a_{i-1\ j+1} &a_{i+1\ j+1}&\cdots&a_{n\ j+1}\\ \vdots&\vdots&&\vdots&\vdots&&\vdots\\ 0&a_{1n}&\cdots&a_{i-1\ n} &a_{i+1\ n}&\cdots&a_{nn}\\ \end{array} \right|\\= (-1)^{i+j-2}a_{ij}\left| \begin{array}{ccc|ccc} a_{11}&\cdots&a_{i-1\ 1} &a_{i+1\ 1}&\cdots&a_{n1}\\ \vdots&&\vdots&\vdots&&\vdots\\ a_{1\ j-1}&\cdots&a_{i-1\ j-1} &a_{i+1\ j-1}&\cdots&a_{n\ j-1}\\ \hline a_{1\ j+1}&\cdots&a_{i-1\ j+1} &a_{i+1\ j+1}&\cdots&a_{n\ j+1}\\ \vdots&&\vdots&\vdots&&\vdots\\ a_{1n}&\cdots&a_{i-1\ n} &a_{i+1\ n}&\cdots&a_{nn}\\ \end{array} \right|$$
です。
再度定理8.を使い、$(-1)^{i+j-2}=(-1)^{i+j}\times(-1)^{-2}=(-1)^{i+j}\times1=(-1)^{i+j}$に注意すると、
$$(-1)^{i+j-2}a_{ij}\left| \begin{array}{ccc|ccc} a_{11}&\cdots&a_{i-1\ 1} &a_{i+1\ 1}&\cdots&a_{n1}\\ \vdots&&\vdots&\vdots&&\vdots\\ a_{1\ j-1}&\cdots&a_{i-1\ j-1} &a_{i+1\ j-1}&\cdots&a_{n\ j-1}\\ \hline a_{1\ j+1}&\cdots&a_{i-1\ j+1} &a_{i+1\ j+1}&\cdots&a_{n\ j+1}\\ \vdots&&\vdots&\vdots&&\vdots\\ a_{1n}&\cdots&a_{i-1\ n} &a_{i+1\ n}&\cdots&a_{nn}\\ \end{array} \right|\\ =(-1)^{i+j}a_{ij}\left| \begin{array}{ccc|ccc} a_{11}&\cdots&a_{1\ j-1} &a_{1\ j+1}&\cdots&a_{1n}\\ \vdots&&\vdots&\vdots&&\vdots\\ a_{i-1\ 1}&\cdots&a_{i-1\ j-1} &a_{i-1\ j+1}&\cdots&a_{i-1\ n}\\ \hline a_{i+1\ 1}&\cdots&a_{i+1\ j-1} &a_{i+1\ j+1}&\cdots&a_{i+1\ n}\\ \vdots&&\vdots&\vdots&&\vdots\\ a_{n1}&\cdots&a_{n\ j-1} &a_{n\ j+1}&\cdots&a_{nn}\\ \end{array} \right|$$
となります。
この右辺の行列式を見てみると、$A$から第$i$行と第$j$列を取り除いた行列の行列式ですので、$\det(A_{ij})$を意味しています。
従って、
$$\begin{eqnarray} &&(-1)^{i+j}a_{ij}\left| \begin{array}{ccc|ccc} a_{11}&\cdots&a_{1\ j-1} &a_{1\ j+1}&\cdots&a_{1n}\\ \vdots&&\vdots&\vdots&&\vdots\\ a_{i-1\ 1}&\cdots&a_{i-1\ j-1} &a_{i-1\ j+1}&\cdots&a_{i-1\ n}\\ \hline a_{i+1\ 1}&\cdots&a_{i+1\ j-1} &a_{i+1\ j+1}&\cdots&a_{i+1\ n}\\ \vdots&&\vdots&\vdots&&\vdots\\ a_{n1}&\cdots&a_{n\ j-1} &a_{n\ j+1}&\cdots&a_{nn}\\ \end{array} \right|\\ &=&(-1)^{i+j}a_{ij}\det(A_{ij})\\ &=&a_{ij}(-1)^{i+j}\det(A_{ij})\\ &=&a_{ij}\tilde{a}_{ij} \end{eqnarray}$$
となります。

以上のことをまとめれば、
$$\left| \begin{array}{c} a_{11}&\cdots&\cdots&a_{1j} &\cdots&\cdots&a_{1n}\\ \vdots&&&\vdots&&&\vdots\\ 0&\cdots&0&a_{ij}&0&\cdots&0\\ \vdots&&&\vdots&&&\vdots\\ a_{n1}&\cdots&\cdots&a_{nj}&\cdots&\cdots&a_{nn}\\ \end{array} \right|=a_{ij}\tilde{a}_{ij}$$ _
です。
この等式は$j=1,2,\dots,n$に対して成り立ちます。
今、どういう状況だったかを思い出すと、
$$\begin{eqnarray} \det(A)&=& \left| \begin{array}{c} a_{11}&\cdots&\cdots&\cdots &a_{1n}\\ \vdots&&&&\vdots\\ a_{i1}&0&\cdots&\cdots&0\\ \vdots&&&&\vdots\\ a_{n1}&\cdots&\cdots&\cdots&a_{nn}\\ \end{array} \right|+ \left| \begin{array}{c} a_{11}&\cdots&\cdots&\cdots &a_{1n}\\ \vdots&&&&\vdots\\ 0&a_{i2}&0&\cdots&0\\ \vdots&&&&\vdots\\ a_{n1}&\cdots&\cdots&\cdots&a_{nn}\\ \end{array} \right|+\cdots\\ &&\cdots+ \left| \begin{array}{c} a_{11}&\cdots&\cdots&\cdots &a_{1n}\\ \vdots&&&&\vdots\\ 0&\cdots&\cdots&0&a_{in}\\ \vdots&&&&\vdots\\ a_{n1}&\cdots&\cdots&\cdots&a_{nn}\\ \end{array} \right| \end{eqnarray}$$
でした。
そして、この等式における第$j$列目の部分をピックアップして考えました。
従って、

• 1列目
  $$\left| \begin{array}{c} a_{11}&\cdots&\cdots&\cdots &a_{1n}\\ \vdots&&&&\vdots\\ a_{i1}&0&\cdots&\cdots&0\\ \vdots&&&&\vdots\\ a_{n1}&\cdots&\cdots&\cdots&a_{nn}\\ \end{array} \right|=a_{i1}\tilde{a}_{i1}$$
• 2列目
  $$\left| \begin{array}{c} a_{11}&\cdots&\cdots&\cdots &a_{1n}\\ \vdots&&&&\vdots\\ 0&a_{i2}&0&\cdots&0\\ \vdots&&&&\vdots\\ a_{n1}&\cdots&\cdots&\cdots&a_{nn}\\ \end{array} \right|=a_{i2}\tilde{a}_{i2}$$
  $\vdots$
• $n$列目
  $$\left| \begin{array}{c} a_{11}&\cdots&\cdots&\cdots &a_{1n}\\ \vdots&&&&\vdots\\ 0&\cdots&\cdots&0&a_{in}\\ \vdots&&&&\vdots\\ a_{n1}&\cdots&\cdots&\cdots&a_{nn}\\ \end{array} \right|=a_{in}\tilde{a}_{in}$$

となるわけですので、
$$a_{i1}\tilde{a}_{i1}+a_{i2}\tilde{a}_{i2}+\dots+a_{in}\tilde{a}_{in}=\det(A)$$
が成り立ちます。

いやあ、疲れましたね。
書いている筆者も疲れちゃいました。
ここで一服しましょう。

終わりましたか？
では続きを行きましょう！

(2.の証明)

「1.の証明が長すぎて覚えてねえよ」と思いますので、再掲します。

$$a_{i1}\tilde{a}_{k1}+a_{i2}\tilde{a}_{k2}+\dots+a_{in}\tilde{a}_{kn}=0,\quad (i\neq k)$$

これを示します。

行列$A$と$k(\neq i)$に対して、第$k$行以外は$A$と同じで、第$k$行を第$i$行で置き換えた行列を$B=\left( b_{ij}\right)$とします。
すなわち、
$$B= \begin{pmatrix} a_{11}&\cdots &a_{1n}\\ \vdots&&\vdots\\ a_{i1}&\cdots&a_{in}\\ \vdots&&\vdots\\ a_{i1}&\cdots&a_{in}\\ \vdots&&\vdots\\ a_{n1}&\cdots&a_{nn}\\ \end{pmatrix} \begin{array}{c} \\ \leftarrow i行\\ \\ \leftarrow k行 \\ \\ \end{array}$$
とします。
この行列$B$の第$i$行と第$k$行は一致しているので、次の命題を使います。

この命題9.の証明は【線型代数学の基礎シリーズ】行列式編 その3を御覧ください。

命題9.により、$\det(B)=0$です。
また、行列$A$と$k(\neq i)$に対して、第$k$行以外は$A$と同じで、第$k$行を第$i$行で置き換えた行列が$B=\left( b_{ij}\right)$なのですから、任意の$j=1,2,\dots,n$に対して
$$B_{kj}=A_{kj},\quad b_{kj}=a_{kj}$$
が成り立ちます。
この第１式から、
$$\tilde{b}_{kj}=(-1)^{k+j}\det(B_{kj})=(-1)^{k+j}\det(A_{kj})=\tilde{a}_{kj}$$
従って、1.を使うと、
$$b_{k1}\tilde{b}_{k1}+b_{k2}\tilde{b}_{k2}+\dots+b_{kn}\tilde{b}_{kn}=\det(B)=0$$
です。
故に、
$$\tilde{b}_{kj}=\tilde{a}_{kj},\quad b_{kj}=a_{kj}$$
を使うと、
$$a_{i1}\tilde{a}_{k1}+a_{i2}\tilde{a}_{k2}+\dots+a_{in}\tilde{a}_{kn}=\det(A),\quad (i\neq k)$$
が得られます。

定理4.の証明終わり

余因子展開（列編）

列についての余因子展開もありますが、本質的には行の余因子展開と同じですので、証明は省略します。
行の余因子展開において$i$行の部分を$j$列にすれば全く同じように証明できます。

いっちょ、余因子展開を使ってみっか

使ってみましょう。

例3.
$$A= \begin{pmatrix} 1&2&0\\ 3&5&-1\\ 4&6&7 \end{pmatrix}$$
として、$A$の行列式を余因子展開により求めてみましょう。

まず、$\det(A)$はサラスの方法から$\det(A)=-9$となります。
サラスの方法とは以下でした。

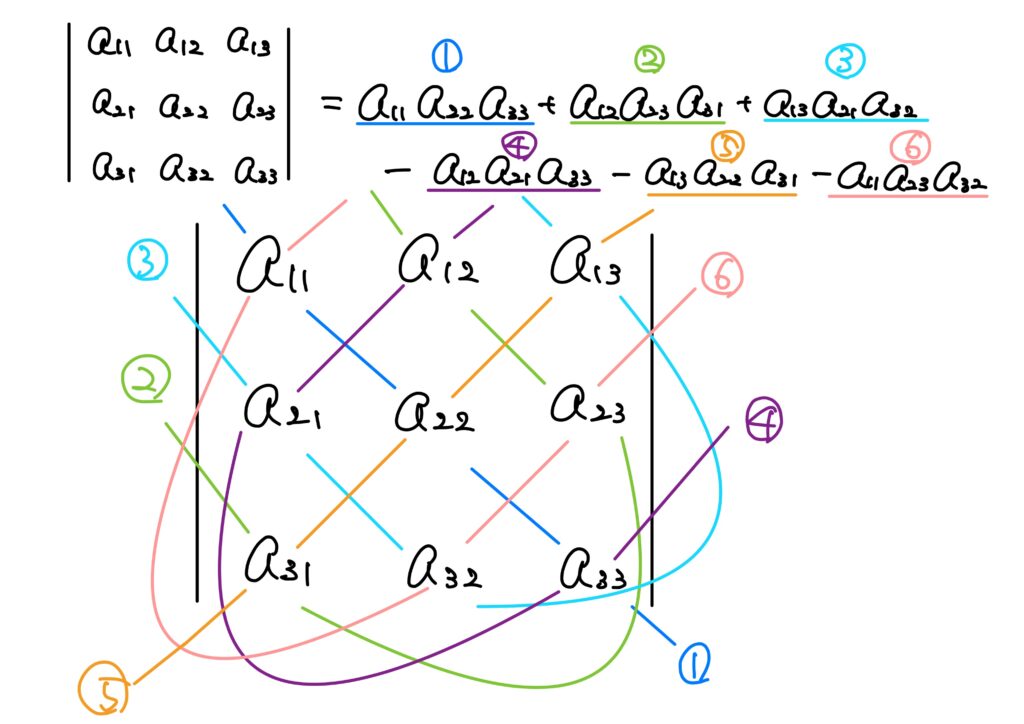
さて、$A$の各$a_{ij}$に対する余因子はすでに求めてありますので、それを使います。

$$\begin{eqnarray} a_{11}\tilde{a}_{11}+a_{12}\tilde{a}_{12}+a_{13}\tilde{a}_{13}&=& 1\times41+2\times(-25)+0\times(-2)\\ &=&41-50\\ &=&-9=\det(A) \end{eqnarray}$$

確かに成り立ちました。

余因子行列

余因子行列は一言で言えば、

です。
この余因子行列は行列の逆行列を求める際に重要な役割を果たします。

筆者もよく間違えちゃいましたが、余因子行列は、余因子を成分とする行列を転置した行列です。

次の定理は行列の逆行列を求めるにあたって重要なステップとなる定理です。

これはとてつもない事実です。
というもの、$\det(A)\neq0$であれば、
$$A\left(\frac{1}{\det(A)}\tilde{A}\right)=\left(\frac{1}{\det(A)}\tilde{A}\right)A=I_n$$
が成り立つわけですので、$\displaystyle\frac{1}{\det(A)}\tilde{A}$が$A$の逆行列となるわけです。

定理11.の証明

$n\in\mathbb{N}$、$A$を$n$次正方行列、$\tilde{A}$を$A$の余因子行列として、
$$A= \begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ a_{n1}&a_{n2}&\cdots &a_{nn}\\ \end{pmatrix},\quad \tilde{A}= \begin{pmatrix} \tilde{a}_{11}&\tilde{a}_{21}&\cdots &\tilde{a}_{n1}\\ \tilde{a}_{12}&\tilde{a}_{22}&\cdots &\tilde{a}_{n2}\\ \vdots&\vdots& \ddots&\vdots\\ \tilde{a}_{1n}&\tilde{a}_{2n}&\cdots &\tilde{a}_{nn}\\ \end{pmatrix}$$
と書いたとします。
このとき、$A\tilde{A}$は
$$\begin{eqnarray} A\tilde{A}&=& \begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ a_{n1}&a_{n2}&\cdots &a_{nn}\\ \end{pmatrix} \begin{pmatrix} \tilde{a}_{11}&\tilde{a}_{21}&\cdots &\tilde{a}_{n1}\\ \tilde{a}_{12}&\tilde{a}_{22}&\cdots &\tilde{a}_{n2}\\ \vdots&\vdots& \ddots&\vdots\\ \tilde{a}_{1n}&\tilde{a}_{2n}&\cdots &\tilde{a}_{nn}\\ \end{pmatrix}\\ &=& \begin{pmatrix} \displaystyle\sum_{h=1}^na_{1h}\tilde{a}_{1h}&\displaystyle\sum_{h=1}^na_{1h}\tilde{a}_{2h}&\cdots &\displaystyle\sum_{h=1}^na_{1h}\tilde{a}_{nh}\\ \displaystyle\sum_{h=1}^na_{2h}\tilde{a}_{1h}&\displaystyle\sum_{h=1}^na_{2h}\tilde{a}_{2h}&\cdots &\displaystyle\sum_{h=1}^na_{2h}\tilde{a}_{nh}\\ \vdots&\vdots& \ddots&\vdots\\ \displaystyle\sum_{h=1}^na_{nh}\tilde{a}_{1h}&\displaystyle\sum_{h=1}^na_{nh}\tilde{a}_{2h}&\cdots &\displaystyle\sum_{h=1}^na_{nh}\tilde{a}_{nh}\\ \end{pmatrix} \end{eqnarray}$$
です。
この行列の第$(i,k)$成分は
$$\sum_{h=1}^na_{ih}\tilde{a}_{kh}$$
です。
ここで、定理4.により、
$$\sum_{h=1}^na_{ih}\tilde{a}_{kh}= \begin{cases} \det(A)& (i=k)\\ 0& (i\neq k) \end{cases}$$
です。
故に、
$$A\tilde{A}= \begin{pmatrix} 1&&\huge{O}\\ &\ddots& \\ \huge{O}&&1 \end{pmatrix}=\det(A)I_n$$
が成り立ちます。

同様にして、$\tilde{A}A$の第$(ik)$成分は、
$$\sum_{h=1}^n\tilde{a}_{hi}a_{hk}$$
です。
これもまた定理4.により、
$$\sum_{h=1}^n\tilde{a}_{hi}a_{hk}= \begin{cases} \det(A)& (i=k)\\ 0& (i\neq k) \end{cases}$$
です。
従って、
$$\tilde{A}A= \begin{pmatrix} 1&&\huge{O}\\ &\ddots& \\ \huge{O}&&1 \end{pmatrix}=\det(A)I_n$$
となるため、成り立ちます。

定理11.の証明終わり

結

今回は余因子、余因子展開、余因子行列について解説しました。
また、余因子展開は行列式を求めるにあたって重要な事実で、余因子行列は逆行列を求めるにあたって重要な概念です。

それ故、余因子は線型代数の中で非常の重要な位置を占めています。

次回は正則行列の必要十分条件、すなわち逆行列が存在するための必要十分条件について解説します。

乞うご期待！質問、コメントなどお待ちしております！