「行列式とその性質①」【線型代数学の基礎シリーズ】行列式編 その2

本記事の内容

本記事は、行列式とその性質のうちの１つを解説する記事です。

本記事を読むにあたり、置換、巡回置換、互換、置換の符号について知っている必要があるため、以下の記事も合わせてご覧ください。

「行列式のための準備(置換、巡回置換、互換、置換の符号 )」【線型代数学の基礎シリーズ】行列式編 その1

...

for-spring.com

2022.07.05

行列式

線型代数を学ぶとき、絶対に避けては通れないのが行列式です。
もはや線型代数を学ぶ意味の１つに「行列式を理解する」ということが含まれていると思います。
それくらい重要です。

行列式って何スか？

行列式を一言で表すのは誠に難しいのですが、強いて言えば、

です。
個人的には「行列式とは何か？」ということを一言で表すよりも、むしろ行列式があることで受ける恩恵の方にこそ意味があると思います。
その恩恵については徐々に解説していきますが、１つは逆行列の導出に必要です。
また、逆行列の存在の必要十分条件に行列式の値が関係してきます。

「なんで逆行列を求めることが重要なの？」という話ですが、それは以前の記事でサラッと述べた、連立一次方程式の解を導く際に使うからです。
「連立一次方程式ってそんなに重要かネ？」と思うかもしれませんが、実は機械学習は行列演算をしていて、簡単に(誠に平たく言うと)連立方程式を解いているので、重要でありかつ我々は知らぬ間に恩恵を受けています。

高校数学の復習($(2,2)$型の行列の行列式)※高校数学で行列を学んでない方でも大丈夫です。

高校数学で行列を学んでいる方は復習として、学んでいない方は「2次元の場合の行列式はこれなんだ〜」というイメージを掴むために読んでいただけると嬉しいです。

さて、ここはサラッと行きます。

※高校数学ではもっとやんわり学んだと思いますが(笑)

このように、正方行列の成分を四則演算して得られる数のことを行列式と呼びます。
ちなみに、実行列の場合は行列式は実数ですが、複素行列の場合の行列式は複素数になる場合もありますので、「数」という少々抽象的な表現を用いています。

このブログを通して読んでいただいている方(本当に嬉しい)であれば、「じゃあ、$\det$ってのは正方行列に対して値(実行列の場合は実数)を対応させる写像なのね。実行列の場合は実数値関数か。」と思っていただけると鋭いです。

$(n,n)$型の行列の行列式は何スか？

では、この$n$次正方行列の行列式とは何か、ということを説明します。

「ﾅﾝｼﾞｬｺﾚ(° ∀。)?」となると思います。
かくいう筆者も初めてこれをみたときに「なーにを言っとるだ貴様？」と思いました。

$n$次正方行列$A$の行列式

$$\det(A)=\sum_{\sigma\in S_n}{\rm sgn}(\sigma)a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}$$
を観察してみましょう。
まず、$\sigma$と$S_n$ですが、

であり、$S_n$は$M_n=\{1,2,\dots,n\}$の置換全体からなる集合でした。
詳しくは、【線型代数学の基礎シリーズ】行列式編 その1を御覧ください。

次に、$\displaystyle\sum_{\sigma\in S_n}$ですが、これは任意の$\sigma\in S_n$に対しての和ですので、$n!$個の置換$\sigma\in S_n$すべてでの和ということです。

第3に、${\rm sgn}(\sigma)$ですが、これは単に置換$\sigma$が何個の互換の積でかけるかで$1$か$-1$です。
ちなみに

でした。
詳しくは、【線型代数学の基礎シリーズ】行列式編 その1を御覧ください。

最後に、$a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}$です。
「ﾅﾝｼﾞｬｺﾚ」の種はこれだと思います。
しかし、ちゃんと見るとなんてことないんですね、実は。
見た目がイカツイだけで、割と優しいです。
強面のお兄さんが実は優しい、みたいな話です。

そんなことは置いておいて、観察しましょう。
文章で述べても分かりにくいかもしれませんので、下記の図と共に読んでいただけると理解しやすいと思います。
結論から言ってしまうと、

です。
$\sigma$は$M_n\{1,2,\dots,n\}$の置換ですので、各列からも、列の中でダブることなくちょうど1つずつ取ってきている、ということが分かります。

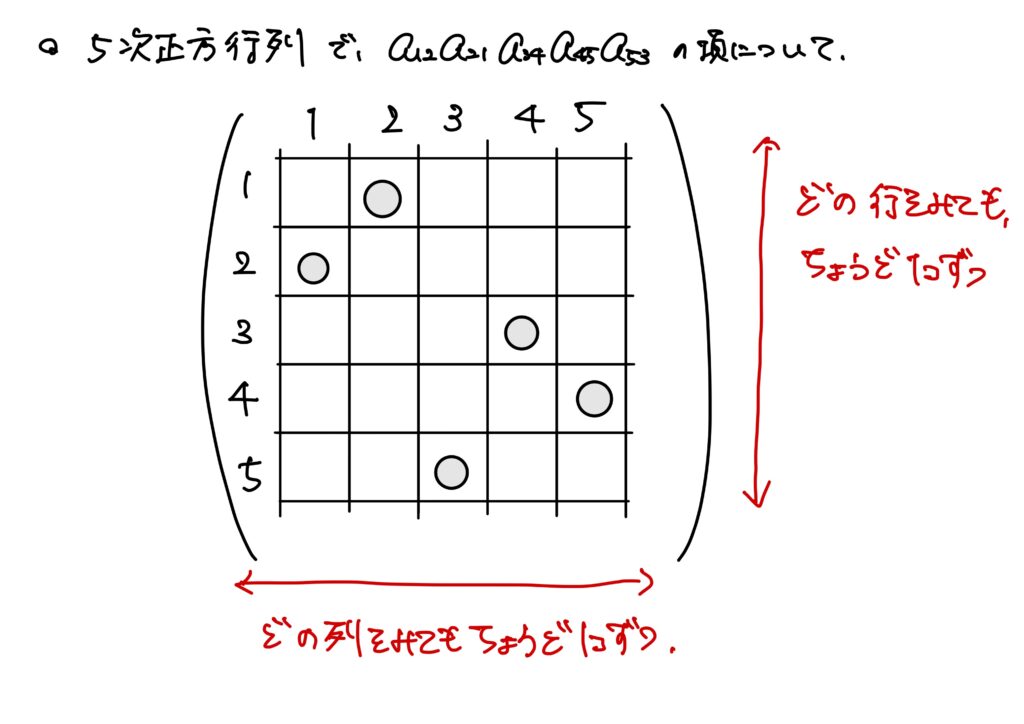
以上のことをまとめると、

ということです。

先程描いた図の場合の${\rm sgn}(\sigma)a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}$を計算してみましょう。

例1.
$$A= \begin{pmatrix} a_{11}&a_{12}&a_{13}&a_{14}&a_{15}\\ a_{21}&a_{22}&a_{23}&a_{24}&a_{25}\\ a_{31}&a_{32}&a_{33}&a_{34}&a_{35}\\ a_{41}&a_{42}&a_{43}&a_{44}&a_{45}\\ a_{51}&a_{52}&a_{53}&a_{54}&a_{55}\\ \end{pmatrix}$$
において、$a_{12}a_{21}a_{34}a_{45}a_{53}$の項を見ると、確かに各行、列からダブらず１つずつ成分を使っていて、
$$(1,2),\ (2,1),\ (3,4),\ (4,5),\ (5,3)$$
の組ですので、対応する置換$\sigma$は
$$\sigma= \left( \begin{array}{c} 1&2&3&4&5\\ 2&1&4&5&3\\ \end{array} \right)$$
です。
従って、この項は
$${\rm sgn}(\sigma)a_{1\sigma(1)}a_{2\sigma(2)}a_{3\sigma(3)}a_{4\sigma(4)}a_{5\sigma(5)}$$
です。
ここで、
$$\sigma=(1\ 2)(3\ 4\ 5)=(1\ 2)(3\ 5)(3\ 4)$$
となるので、$\sigma$は３つの互換の積で書けるから
$${\rm sgn}(\sigma)=-1$$
となります。
故に、
$$-a_{12}a_{21}a_{34}a_{45}a_{53}$$
が導けます。
このような$\sigma$は$5!=120$個ある全ての置換で和を取るわけですので、大変です。
「こんなん人間がやることじゃねえだろ」と思っています。

$2$次と$3$次の正方行列の行列式を計算してみる

「2次と3次なら…」と思うかもしれませんが、面倒です。
「まあ、$2次$なら…」という感じですが「そもそも2次の場合は知ってるし…」と思うかもしれません。
確かに暗記してしまえば終いです。
しかし、一度「行列式とは何か」ということからしっかり計算してみることが重要だと思います。

２次正方行列の行列式

例2. $$A= \begin{pmatrix} a_{11}&a_{12}\\ a_{21}&a_{22}\\ \end{pmatrix}$$
の行列式を計算してみます。
$M_n=\{1,2\}$ですので、置換は$2!=2$個あり、

ですので、
$${\rm sgn} \begin{pmatrix} 1&2\\ 1&2\\ \end{pmatrix}=1,\quad {\rm sgn} \begin{pmatrix} 1&2\\ 2&1\\ \end{pmatrix}=-1$$
となります。
従って、
$$\begin{eqnarray} \det(A)&=& {\rm sgn} \begin{pmatrix} 1&2\\ 1&2\\ \end{pmatrix}a_{11}a_{22}+ \begin{pmatrix} 1&2\\ 2&1\\ \end{pmatrix}a_{12}a_{21}\\ &=&a_{11}a_{22}-a_{12}a_{21} \end{eqnarray}$$
となります。

3次正方行列の行列式

例3. $$A= \begin{pmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\\ \end{pmatrix}$$
の行列式を計算してみます。
$M_n=\{1,2,3\}$ですので、置換は$3!=6$個あり、その中で偶置換が
$$\begin{eqnarray} \begin{pmatrix} 1&2&3\\ 1&2&3\\ \end{pmatrix}&=&\epsilon,\quad \begin{pmatrix} 1&2&3\\ 2&3&1\\ \end{pmatrix}=(1\ 2\ 3)=(1\ 3)(1\ 2)\\ \begin{pmatrix} 1&2&3\\ 3&1&2\\ \end{pmatrix}&=& =(1\ 3\ 2)=(1\ 2)(1\ 3) \end{eqnarray}$$
であり、奇置換は
$$\begin{eqnarray} \begin{pmatrix} 1&2&3\\ 2&1&3\\ \end{pmatrix}=(1\ 2),\quad \begin{pmatrix} 1&2&3\\ 3&2&1\\ \end{pmatrix}=(1\ 3),\quad \begin{pmatrix} 1&2&3\\ 1&3&2\\ \end{pmatrix}=(2\ 3) \end{eqnarray}$$
です。
従って、
$$\begin{eqnarray} \det(A)= a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32} \end{eqnarray}$$

このように2次と3次の行列式は割とサクッと求まるのですが、覚えていたほうが便利です。

特に、３次の行列式については図式を使うことで記憶しやすいと思います。

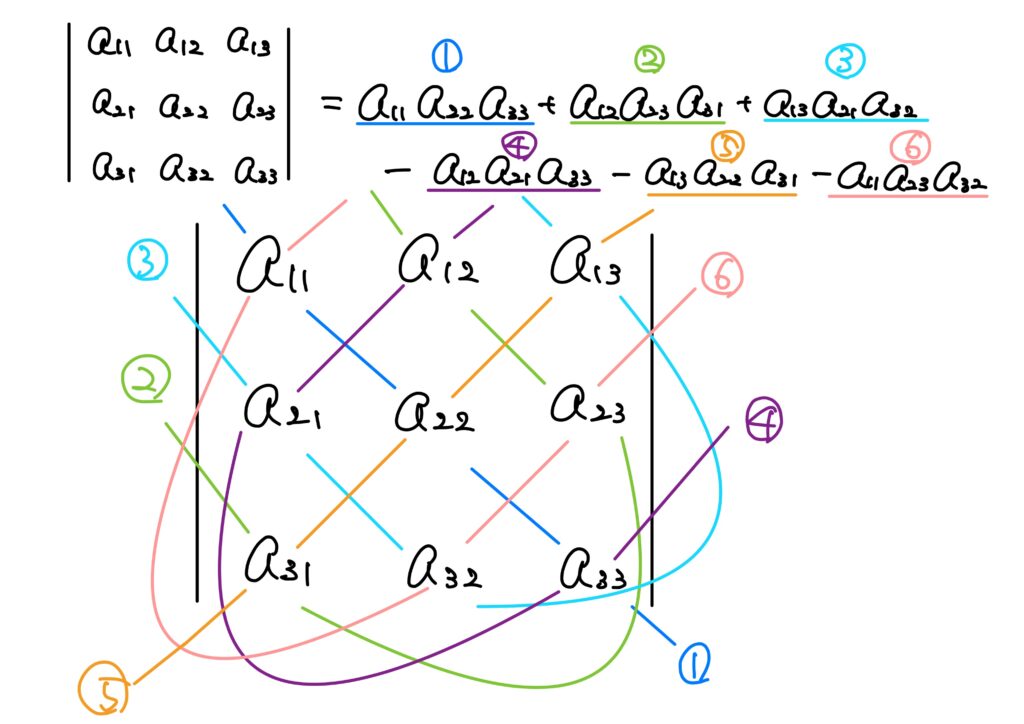
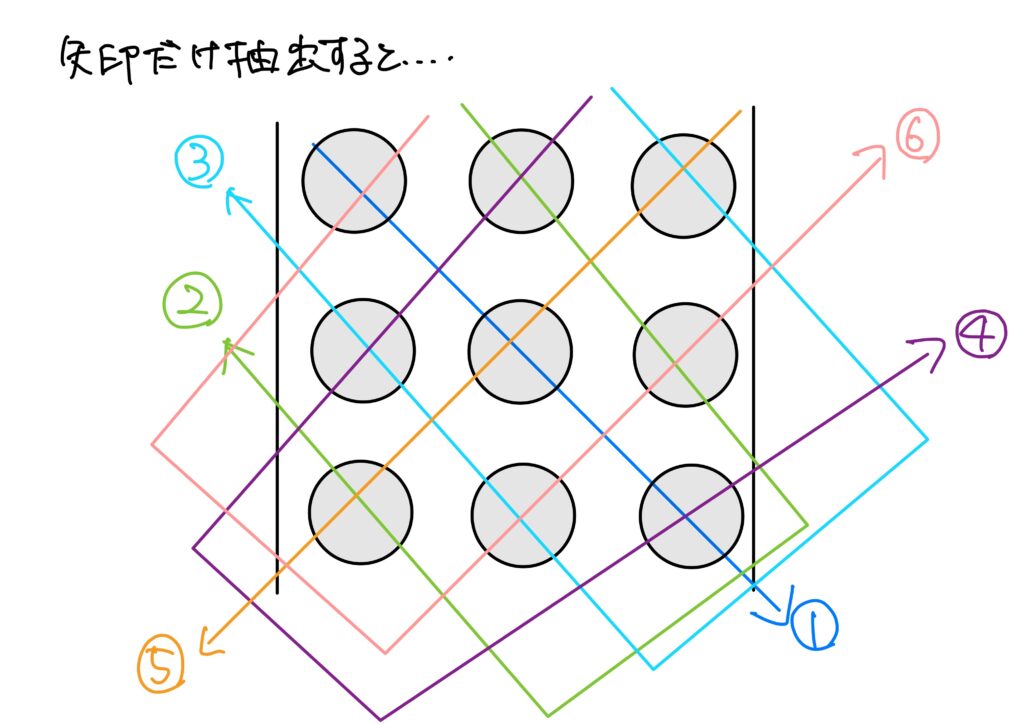
これをサラスの方法といいます。

４次以降の正方行列の行列式はどうすんのよ

４次の場合の行列式は$4!=24$個の項が出現するので、もう面倒くさくてかないません。
さらに４次以降の場合はサラスの方法のように簡単には行かないことに注意してください。

「じゃあどうすんの」という話ですが、それは今回と次回と次次回で解説する「行列式の性質」を使って計算します。

行列式の基本性質①

まず、「次数が大きくなれば計算は面倒だけど、どうすんの」ということについてどういう方針で計算するか、ということを先に述べます。
それは

です。
「え？行列そのものが変わっちゃうんじゃない？」と思うかもしれませんが、それを可能にするのか行列式の性質なのです。

$(1,1)$成分以外の第１列の成分がすべて$0$な正方行列の行列式

まずは、性質①として、特別な場合の行列の行列式が、次数が少ない行列の行列式に帰着できる、という定理を紹介、証明します。

これは確かに、次数が下がっています。

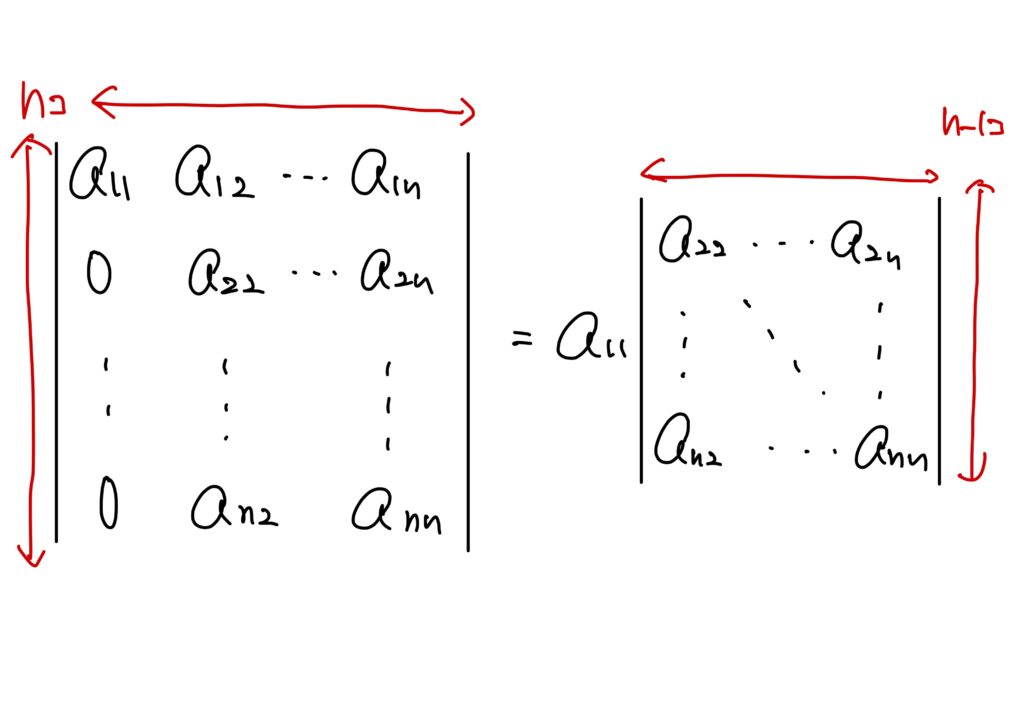
この定理4.の主張するところは、第１列ベクトルの第１成分以外が$0$であるような行列は、その$(1,1)$成分と、第１列ベクトルと第１行ベクトルを除いた$n-1$次正方行列の行列式と一致する、ということです。

では、証明します。

定理4.の証明

$n\in\mathbb{N}$、$A$を$n$次正方行列とし、
$$A= \begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ a_{n1}&a_{n2}&\cdots &a_{nn}\\ \end{pmatrix}$$
と書いたとします。
またこのとき、
$$a_{21}=a_{31}=\dots=a_{n1}=0$$
とします。
この$A$の行列式は
$$\sum_{\sigma\in S_n}{\rm sgn}(\sigma)a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}$$
です。
$\sigma(1)\neq1$であるような$\sigma$は、置換であるので、$\sigma(k)=1$となる$k>1$が存在します。
すなわち、$\sigma(1)\neq1$ですので、$1$は$1$と対応しないので、$1$とは別の$k>1$があって、$k$と$1$が対応している、ということです。

今、$\sigma(k)=1$となる$k>1$が存在するわけですので、この$k$に対しては、仮定から
$$a_{k\sigma(k)}=a_{k1}=0$$
です。
従って、
$$a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{k\sigma(k)}\cdots a_{n\sigma(n)}=0$$
すなわち、$\sigma(1)\neq 1$というような行列式の項はすべて$0$です。
故に、$\sigma(1)=1$というような置換$\sigma\in S_n$についてのみ考えればOKです。
具体的には、
$$\sigma= \left( \begin{array}{c} 1&2&\cdots&n\\ 1&i_2&\cdots&i_n\\ \end{array} \right)$$
という場合の置換に関する和にのみ焦点を当てれば良いわけです。

上記の$\sigma$は$n-1$個の文字の集合$M_{n-1}=\{1,2,\cdots,n-1\}$における置換と考えることができます。
つまり、$\sigma\in S_{n-1}$と考えることができます。
実際、$f:M_n^\prime=\{2,3,\dots,n\}\to M_{n-1}$を

• $2\in M_n^\prime$に対して、$f(2)=1\in M_{n-1}$
• $3\in M_n^\prime$に対して、$f(3)=2\in M_{n-1}$
  $\qquad\qquad\qquad\vdots$
• $n\in M_n^\prime$に対して、$f(n)=n-1\in M_{n-1}$

と定めることで$f$は全単射ですので、同一視できます。

従って、
$$\begin{eqnarray} \det(A)&=&\sum_{\sigma\in S_n}{\rm sgn}(\sigma)a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}\\ &=&\sum_{\substack{\sigma\in S_n\\ \sigma(1)=1}}{\rm sgn}(\sigma)a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}\\ &=&\sum_{\sigma\in S_n}{\rm sgn}(\sigma)a_{11}a_{2\sigma(2)}\dots a_{n\sigma(n)}\\ &=&a_{11}\sum_{\sigma\in S_n}{\rm sgn}(\sigma)a_{2\sigma(2)}\dots a_{n\sigma(n)}\\ &=&a_{11} \sum_{\tau\in S_{n-1}}{\rm sgn}(\tau)a_{2\tau(1)}\dots a_{n\tau(n)} \end{eqnarray}$$
ただし、$\tau$は$n-1$文字$\{2,3,\dots,n\}$の置換です。

ここで、$\displaystyle\sum_{\tau\in S_{n-1}}{\rm sgn}(\tau)a_{1\tau(1)}a_{2\tau(2)}\dots a_{n\tau(n)}$を見ると、これはまさに
$$\begin{pmatrix} a_{22}&\cdots &a_{2n}\\ \vdots& \ddots&\vdots\\ a_{n2}&\cdots &a_{nn}\\ \end{pmatrix}$$
の行列式です。
従って、
$$\det(A)= \left| \begin{array}{c} a_{11}&a_{12}&\cdots &a_{1n}\\ 0&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ 0&a_{n2}&\cdots &a_{nn}\\ \end{array}\right|=a_{11} \left| \begin{array}{c} a_{22}&\cdots &a_{2n}\\ \vdots& \ddots&\vdots\\ a_{n2}&\cdots &a_{nn}\\ \end{array}\right|$$
です。

定理4.の証明終わり

三角行列の行列式

まずは三角行列とは何か、ということを説明します。

この三角行列について次のことが成り立ちます。

系5.の証明

定理4.を繰り返し使えば証明可能です。
定理4.から
$$\det(A)=\left| \begin{array}{c} a_{11}&a_{12}&\cdots &a_{1n}\\ 0&a_{22}&\cdots &a_{2n}\\ \vdots&\ddots& \ddots&\vdots\\ 0&\cdots&0 &a_{nn}\\ \end{array}\right|= a_{11} \left| \begin{array}{c} a_{22}&\cdots &\cdots&a_{2n}\\ 0&\ddots &&\vdots\\ \vdots&\ddots&\ddots&\vdots\\ 0&\cdots&0 &a_{nn}\\ \end{array}\right|$$
です。
再度定理4.から
$$a_{11} \left| \begin{array}{c} a_{22}&\cdots &\cdots&a_{2n}\\ 0&\ddots &&\vdots\\ \vdots&\ddots&\ddots&\vdots\\ 0&\cdots&0 &a_{nn}\\ \end{array}\right|= a_{11}a_{22} \left| \begin{array}{c} a_{33}&\cdots &\cdots&a_{3n}\\ 0&\ddots &&\vdots\\ \vdots&\ddots&\ddots&\vdots\\ 0&\cdots&0 &a_{nn}\\ \end{array}\right|$$
これを続ければ、
$$\det(A)=a_{11}a_{22}\dots a_{nn}$$
です。

系5.の証明終わり

実は、下三角行列の行列式も対角成分の積と等しいですが、それは転置と行列式の関係を述べてから似します。

行列をの分割と行列式

$X$を$n$次正方行列とします。
このとき、$n=r+s$を満たすような自然数$r,s$に対して、$A$を$r$次正方行列、$B$を$(r,s)$型の行列、$C$を$(s,r)$型の行列、$D$を$s$次正方行列とします。

このとき、$X$を簡略化して、
$$X= \begin{pmatrix} A&B\\ C&D\\ \end{pmatrix}$$
と書きます

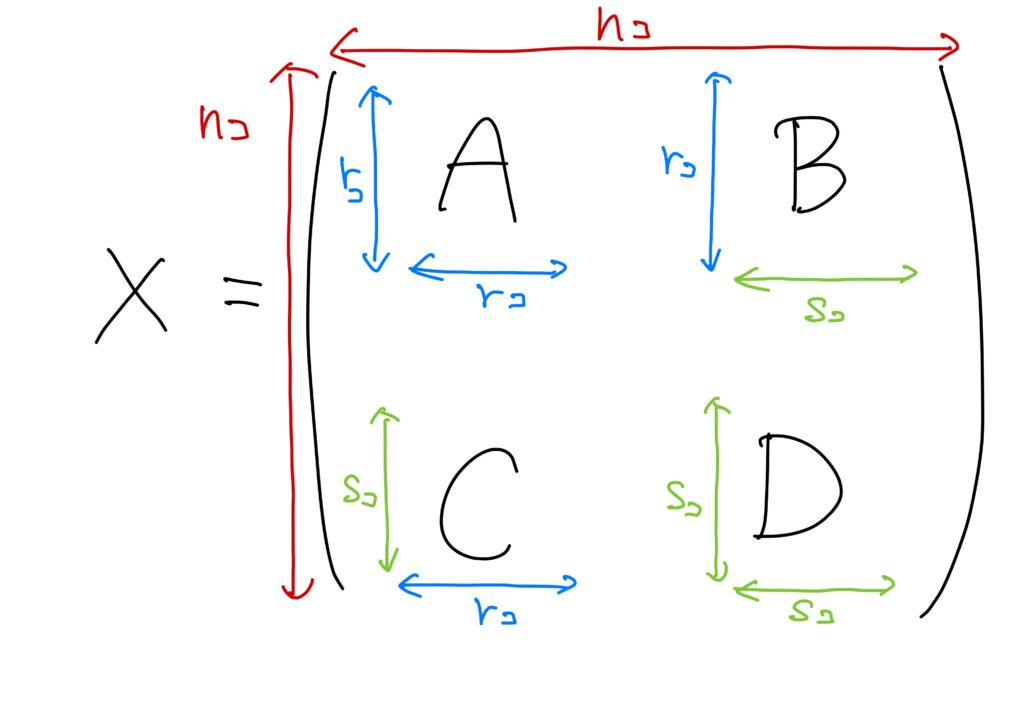
このように行列を分割して書いたとき、次が成り立ちます。

この定理の証明はちょっと面倒ですが、がんばります。

定理6.の証明

$\displaystyle X= \begin{pmatrix} A&B\\ C&D\\ \end{pmatrix}=\left(a_{ij}\right)$($n=r+s$)とします。
$X$の行列式は
$$\sum_{\sigma\in S_n}{\rm sgn}(\sigma)a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}$$
です。
仮定から、$O$は$(s,r)$型の零行列ですので、
$$(\forall i,j\in\mathbb{N};r+1\leq i\leq n,\ 1\leq j\leq r)\quad a_{ij}=0$$
です。
すなわち、$k\geq r+1$、$\sigma(k)\leq r$というような$k$が存在して(言い換えると、$\{\sigma(r+1),\dots,\sigma(n)\}$の中に$r$以下の数があるということ)、その$k$については
$$a_{k\sigma(k)}=0$$
ということです。
これを因子に持つ行列式の項は
$${\rm sgn}(\sigma)a_{1\sigma(1)}\cdots a_{n\sigma(n)}=0$$
となります。
つまり、$|X|$を考える際に、上記の項を持つ$\sigma$については除いてOKということです。
従って、集合として、
$$\{\sigma(r+1),\dots,\sigma(n)\}=\{r+1,\dots,n\}$$
と満たす置換$\sigma$だけを考えればOKです。
ここで、そもそも置換は全単射ですので、
$$\{\sigma(1),\dots,\sigma(r)\}=\{1,\dots,r\}$$
も満たしています。
従って、$\sigma$は上記の２パターンに分かれるということになります。
つまり、$\sigma$は$\{1,2,\dots,r\}$の置換$\tau$と、$\{r+1,r+2,\dots,n\}$の置換$\rho$が存在して、$\sigma=\rho\tau$と書くことができます。

さて、上記を満たす$\sigma$をすべて動かす、ということは、まさに$\tau$と$\rho$をそれぞれ$S_r$と$S_s^\prime$の要素すべてを動かす、ということです。
ただし、$S_s^\prime$は$s$個の文字$\{r+1,\dots,n\}$の置換全体です。

そして、${\rm sgn}$の以下の性質を使います。

この定理7.の証明は【線型代数学の基礎シリーズ】行列式編 その1を御覧ください。

定理7.の1.を使うことによって、
$${\rm sgn}(\sigma)={\rm sgn}(\rho\tau)={\rm sgn}(\rho){\rm sgn}(\tau)$$
ですので、
$$\begin{eqnarray} |X|&=&\sum_{\substack{\tau\in S_r \\ \rho \in S_s^\prime}}{\rm sgn}(\rho\tau)a_{1\tau(1)}\dots a_{r\tau(r)}a_{r+1\rho(r+1)}\dots a_{n\rho(n)}\\ &=&\left( \sum_{\tau\in S_r}{\rm sgn}(\tau)a_{1\tau(1)}\dots a_{r\tau(r)}\right) \left(\sum_{\rho\in S_s^\prime}{\rm sgn}(\rho)a_{r+1\rho(r+1)}\dots a_{n\rho(n)} \right)\\ &=& |A|\cdot |D| \end{eqnarray}$$
となって、成り立ちます。

定理6.の証明終わり

結

今回は、「行列式とは何か」、「行列式を計算するにあたって使う性質の一部」を解説しました。
「行列式とは？」という問に対しては、抽象的ですが、正方行列に対してただ１つ定まる数のことで、これは逆行列の存在条件、逆行列の計算に必要です。

しかし、行列式は定められ方が複雑ですので、いざ行列式が分かっても計算は困難です。
そこで、実際は行列式の性質を使って計算するのですが、その性質の一部を解説しました。

特に、性質として、上三角行列の行列式と行列を部分部分に分割したときの計算方法を解説しました。
後者は特に有用な気もしますが、そもそも高次元の行列を考えると分割したとて高次元なので結局計算は面倒です。

次回はそれを少し緩和する行列式の性質を解説します。

乞うご期待！質問、コメントなどお待ちしております！