「単射って？」【論理と集合シリーズ】写像編 その6

本記事の内容

本記事は「単射って何？」ということについて解説する記事である。

「写像？」となっている方は以下の記事を参照してください。

「写像…?何すか写像って？」〜写像のイメージをつかもう！〜【論理と集合シリーズ】写像編 その１

本記事の内容本記事は「写像...?何すか写像って？」という問に答えるために、写像のイメージを説明する記事である。「写像とはこれのことです！」ということは後の記事で述べることにして、本記事ではあくまでイメージを伝える。写像は関数の極限を語る上

for-spring.com

「写像って数学的に何？」「結局、関数と同じでは？」【論理と集合シリーズ】写像編 その３

本記事の内容本記事は、「写像って数学的に何のこと？」ということに答える記事である。写像は数学の専門書でも「対応」やら「規則」やらという抽象的な表現で語れれることもしばしばである。今回は素朴な立場と厳密な立場の２立場で説明する。で、何すか写像

for-spring.com

単射

「単射って何？」というと、要は「定義域の異なる要素は、対応する終域の要素も異なるような写像のこと。」ということである。
これを前回書いた例を少々改変したver.で見てみよう。

例1′.(料理を食べるときに使う食器との対応規則の改変ver.)
$X’=\{カレー,ステーキ、おにぎり\}$、$Y’=\{スプーン,ナイフ,手,足\}$とする。
このとき、カレーはスプーンで食べるため(手で食べる人もいるだろうが、日本人では極めて稀だと思うので排除している)、カレーとスプーンを対応させる。
同様にステーキはスプーンでは食べず、手で食べると熱い。
同様に足で食べる人もいない(見たことがない)。
ステーキはかじりつくのではなくナイフで切って小分けにして食べる。
故にステーキはナイフと対応させる。
おにぎりを食べるときにスプーン、ナイフ、足を使うことはないだろう(お上品な方は使うかもしれないが、筆者のような庶民には無縁)。
従って、おにぎりと手を対応させる。
この対応規則を$h_0$と書くとき、今述べた

1. カレーとスプーン
2. ステーキとナイフ
3. おにぎりと手

という対応関係は、

1. $h_0(カレー)=スプーン$、
2. $h_0(ステーキ)=ナイフ$、
3. $h_0(おにぎり)=手$

と書かれるのだった。
このとき、カレー、ステーキ、おにぎりはそれぞれスプーン、ナイフ、手に対応しているので、カレー、ステーキ、おにぎりは別々の$Y$の要素と対応している。
すなわち、任意の定義域の別々要素が終域の別々の要素と対応しているとき、その対応(写像)は単射であるという。
そもそも写像は、定義域の要素が終域の要素ただ１つと対応していれば良いので、定義域の異なる要素が終域の同じ要素と対応していても良い。
勿論、定義域の異なる要素が終域の異なる要素と対応していても良い。
このときに写像は単射である、というわけである。

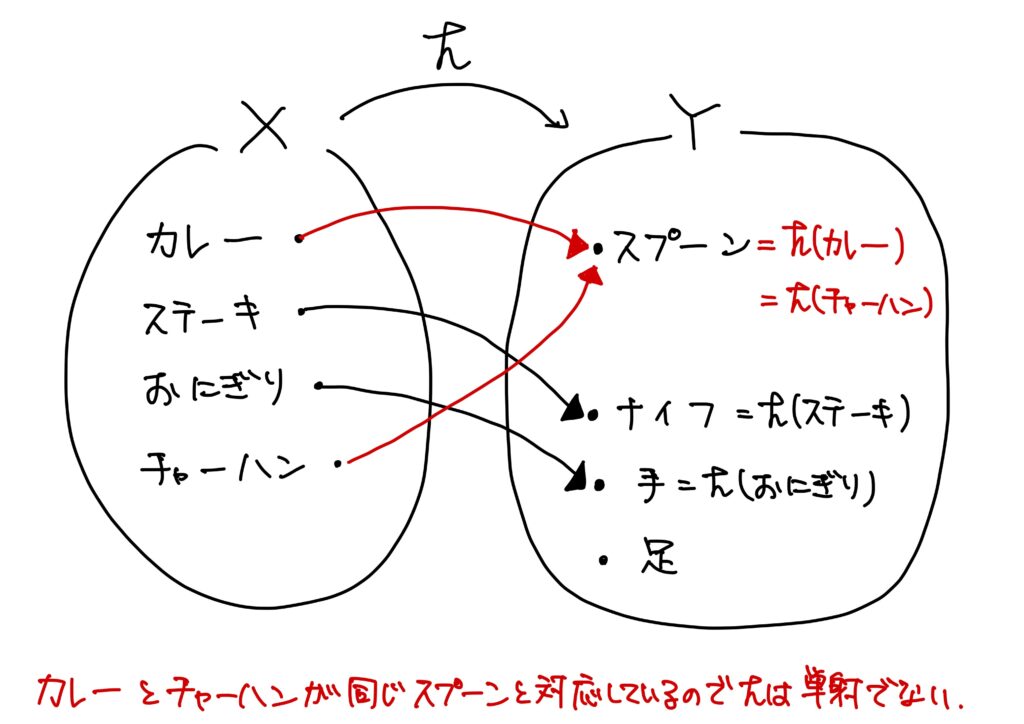
ちなみに、前回の記事においての例1.は、$X=\{カレー,ステーキ、おにぎり,チャーハン\}$、$Y=\{スプーン,ナイフ,手,足\}$とし、

1. カレーとスプーン
2. ステーキとナイフ
3. おにぎりと手
4. チャーハンとスプーン

という対応だった。
つまり、

1. $h(カレー)=スプーン$、
2. $h(ステーキ)=ナイフ$、
3. $h(おにぎり)=手$、
4. $h(チャーハン)=スプーン$

だった。
この場合、カレーとチャーハンがスプーンという同じ要素に対応してしまっているので、この$h:X\to Y$は写像だが、単射ではない。

例2.(数学っぽい例)
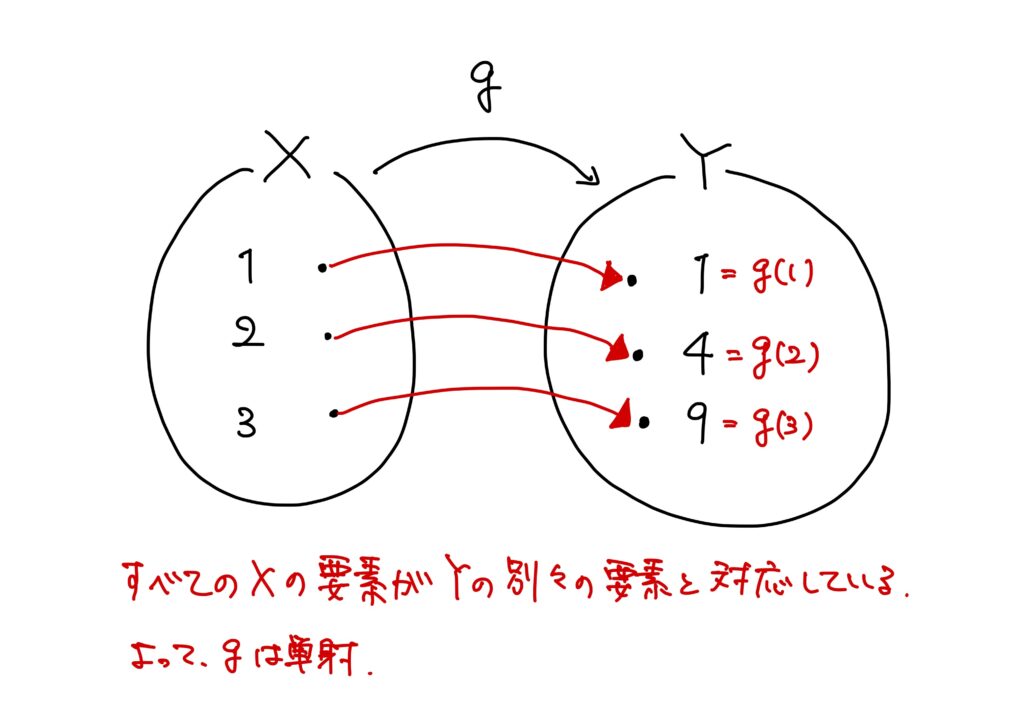
$X=\{1,2,3\}$、$Y=\{1,4,9\}$とする。
$X$の要素$1,2,3$に対して$Y$の要素$1,4,9$を次のように対応させる。

1. $1\in X$と$1\in Y$、
2. $2\in X$と$4\in Y$、
3. $3\in X$と$9\in Y$。

この対応規則を$g$と書く。
このとき、

1. $g(1)=1$、
2. $g(2)=4$、
3. $g(3)=9$。

である。
この例においても、
$1,2,3\in X$はそれぞれ$1,4,9\in Y$に対応しているので、$1,2,3\ X$は別々の$Y$の要素と対応している。
すなわち、任意の定義域の別々要素が終域の別々の要素と対応している。
従って$g:X\to Y$は単射である。

例3.(実数値の関数)
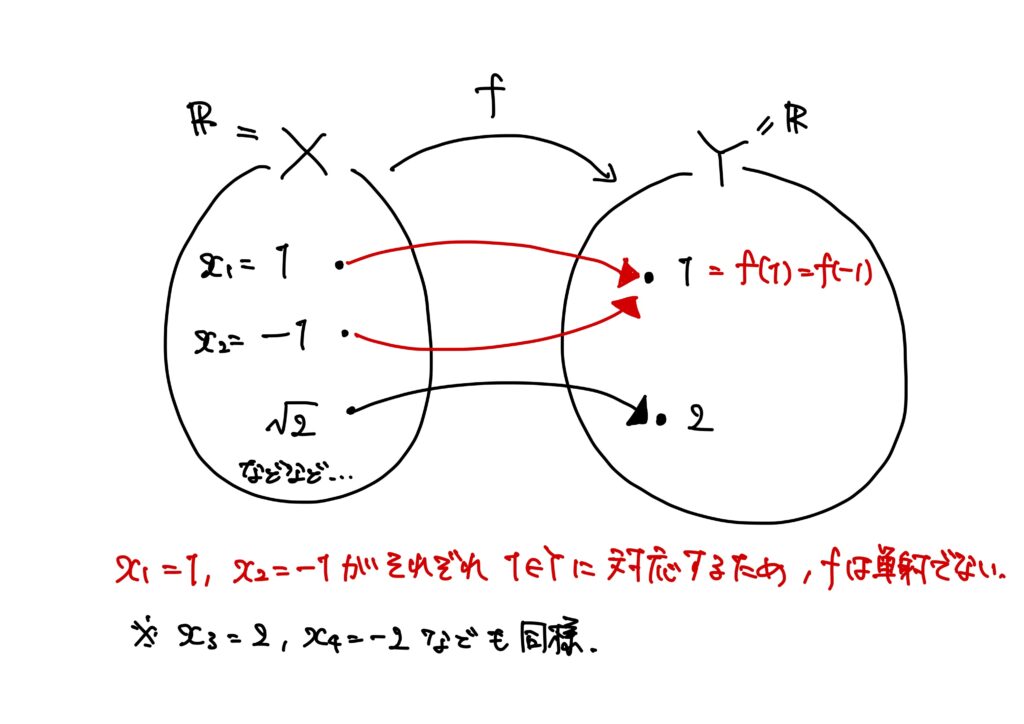
$X=Y=\mathbb{R}$とする。
このとき、任意の$x\in X=\mathbb{R}$に対して、$Y=\mathbb{R}$の要素$y$と$x^2$とを対応させる。
すなわち、任意の$x\in X$に対して、$y\in Y$を$y=x^2$で対応させる、と言っているわけである。
つまりこの対応規則$f$は
$$(\forall x\in X)\ f(x)=x^2$$
ということである。
この$f$は単射ではない。
実際、$x_1=1$、$x_2=-1$とすると、$f(x_1)=f(x_2)=1$であるため、$x\in X$が相異なっていても同じ$y\in Y$と対応しているからである。

これを論理式で書くと、次である。

「単射であることを示しなさい！」と言われたらば上記の命題を示しなさい、ということである。

！注意！
筆者の経験なのだが、若干古めの数学書には、単射よりも一対一という表記が多く現れる気がする。
しかし、筆者はあまり好きではない(勿論、好き好きなので、しっくり来る呼び名を使ってもらって構わない)。
というのも、一対一と言われると「定義域$X$と終域$Y$の全ての要素に対応がある。」ような気がするからである。
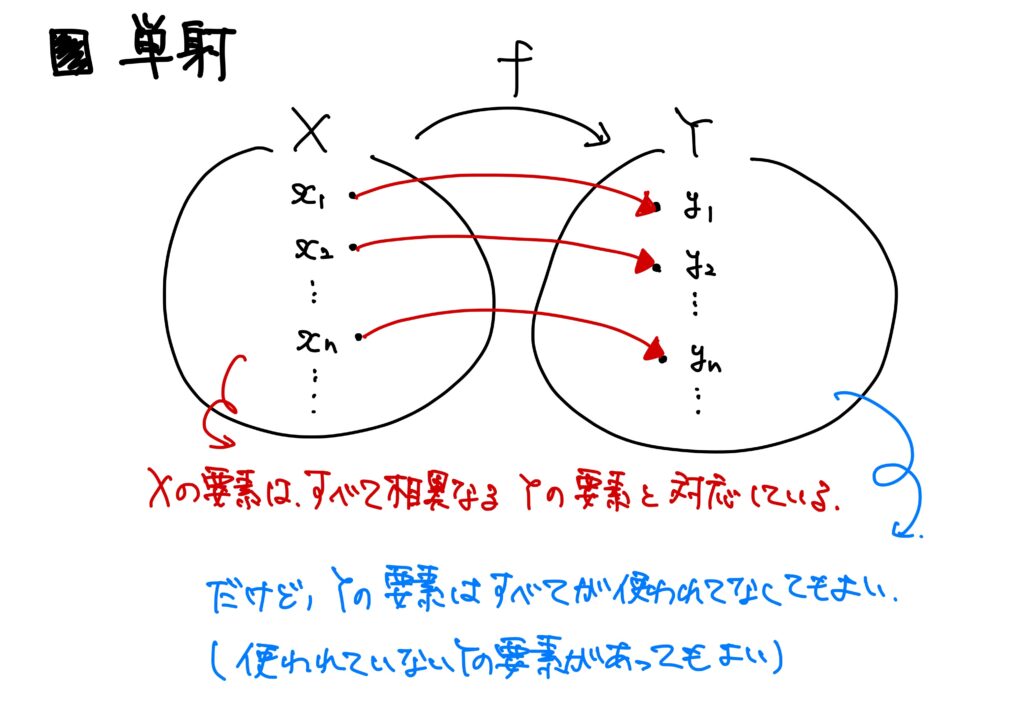
しかし、単射は$(\forall x,x’\in X)\ (f(x)= f(x’)\Rightarrow x=x’)$が成り立つことなのだから、終域$Y$の要素は全て使われていなくても良い(使われていない要素があってもよい)。
そういう意味では筆者は単射と呼んでいる。
※勿論、単射と一対一のどちらでも通じます。

結

今回は単射について説明した。
とどのつまり、単射というのは「定義域の別々の要素は、終域の別々の要素と対応するような写像」である。
しばしば対偶をとって、「終域の同じ要素と対応するのであれば、定義域の要素も同じ。」という捉え方をすることもある。
これらは同値なのでどちらを採用しても良い。

筆者は対偶ver.の方をよく用いる。
というのも、「〇〇と△△が等しい。」ということを証明するのと「〇〇と△△は等しくない。」ということを証明するのとでは前者の方が考えやすいからである。

次回は「全射」について説明する。

乞うご期待！質問、コメントなどお待ちしております！