本記事の内容
本記事は「合成写像って何?」ということについて解説する記事である。
「写像?」となっている方は以下の記事を参照してください。
合成写像
とどのつまり、合成写像は高校数学で学んだ合成関数の写像ver.である。
筆者の感覚だが、合成写像は微積分の分野で活躍する概念だと思う。
というのも、一見複雑そうな関数でも、新たな変数(パラメータ)を用意してそのパラメータを経由させることで関数自体を簡素化させて理解しやすくなる場合があるからである。
ここでは述べないのだが、ニューラルネットワークの核にも合成関数が使われている。
例えば、次のような場合を考えてみる。
例5.(合成写像)
- \(A=\)日本国民の集合,
- \(B=\)全ての年齢からなる集合,
- \(C=\)全ての年齢区分からなる集合\(=\{0\sim14歳の区分,15\sim64歳の区分,65歳\simの区分\}\)
とする。
写像\(f:A\to B\)を任意の日本国民\(a\in A\)に対して、\(f(a)=a\)の年齢として定める。
また、写像\(g:B\to C\)を任意の年齢\(b\in B\)に対して、\(g(b)=b\)が属す年齢区分として定める。
このとき、\(h:A\to C\)を\(h(a)=g(f(a))\)で定める。
すなわち、\(h\)は、任意の日本国民\(a\in A\)に対して、\(a\)が属する年齢区分を対応させる写像である。
※\(f\)も\(g\)も写像として定まっているのだから、\(g(f(a))\)も定まる。
このとき、\(h\)を\(h=g\circ f\)と書く。
つまり、\(h(a)=(g\circ f)(x)=g(f(a))\)である。
この\(h\)のこと、すなわち\(g\circ f\)のことを\(f\)と\(g\)の合成写像という。
実際に展開してみると、
\begin{eqnarray}
h(a)&=&(g\circ f)(a)\\
&=&g(f(a))\\
&=&g(aの年齢)\\
&=&aの年齢が属する年齢区分\\
&=&aが属する年齢区分
\end{eqnarray}
となる。

例6.(合成関数)
- \(X=\mathbb{R}\),
- \(Y=[-1,1]\),
- \(Z=\mathbb{R}\)
とし、
- \(f:X\to Y\)を任意の\(x\in X\)に対して、\(f(x)=\sin x\),
- \(g:Y\to Z\)を任意の\(y\in Y\)に対して、\(g(y)=2^y\),
とする。
このとき、\(g\circ f:X\to Z\)を\((g\circ f)(x)=g(f(x))\)で定める。
この\(g\circ f\)を\(f\)と\(g\)の合成写像(合成関数)という。
ここで、
\begin{eqnarray}
(g\circ f)(a)&=&g(f(x))\\
&=&g(\sin x)\\
&=&2^{\sin x}
\end{eqnarray}
である。
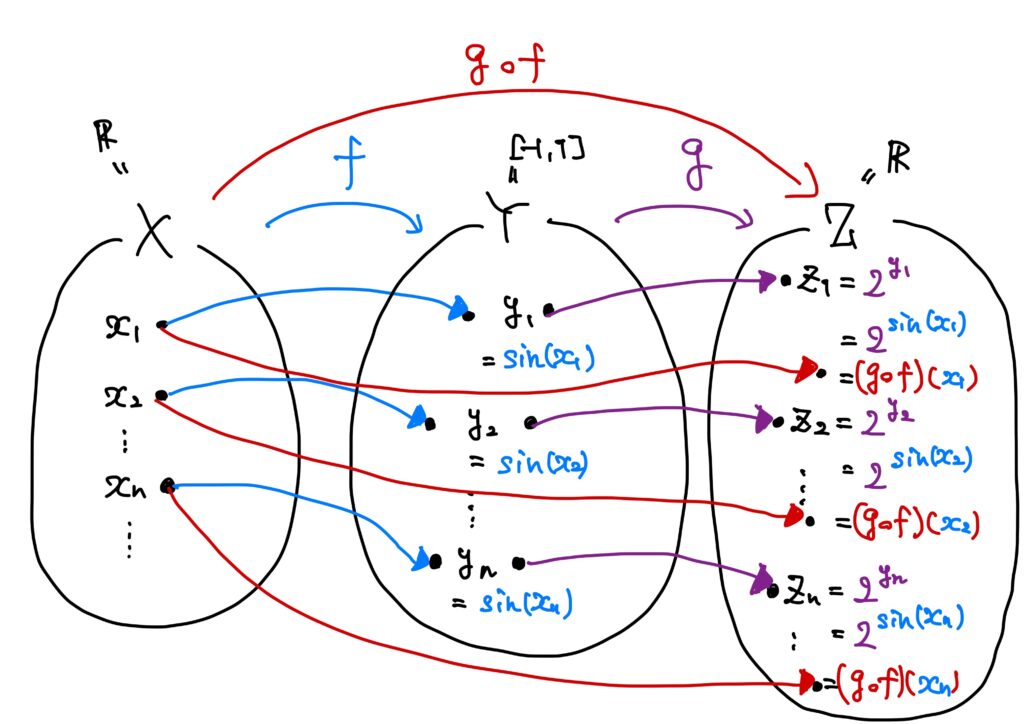
このように、2つの集合にもう1つの集合を加えて、その加えた集合を経由させる写像を合成写像という。
これを式で表すと次である。
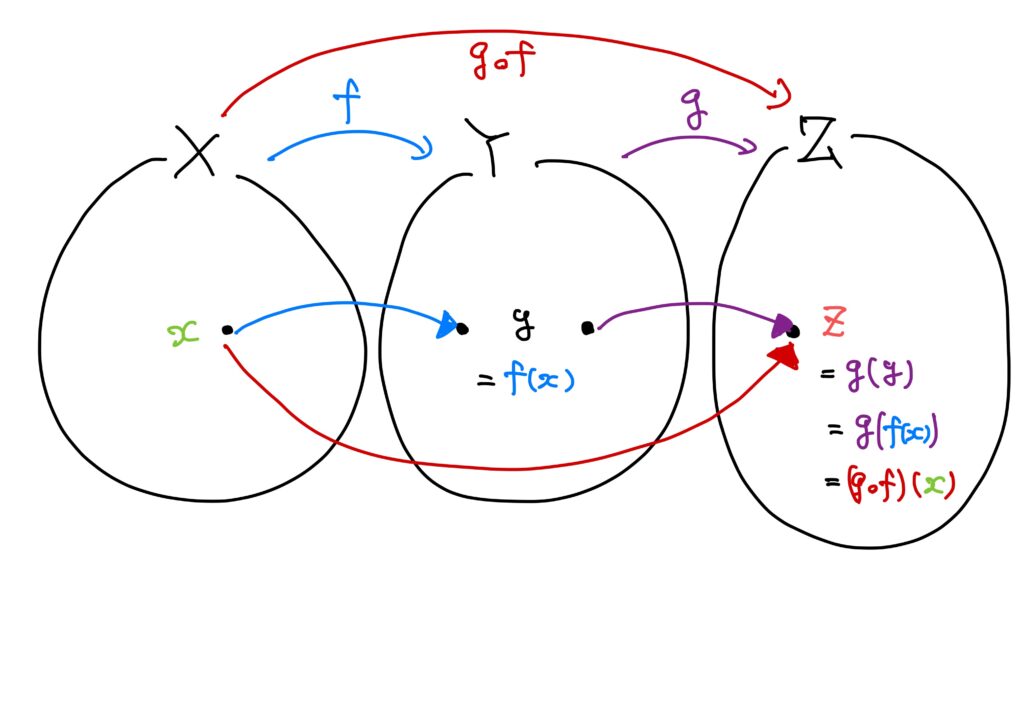
\(f:X\to Y\)、\(g:Y\to Z\)を写像とする。このとき、写像\(h:X\to Z\)を $$h(x)=g(f(x))\ (x\in X)$$ で定める。この\(h\)を\(f\)と\(g\)の合成(the composition of \(f\) and \(g\))、あるいは合成写像(the composite mapping)と呼び、\(g\circ f\)で表す。 すなわち、\(g\circ f:X\to Z\)は $$(g\circ f)(x)=g(f(x))\ (x\in X)$$ で定められる写像である。 また、このとき\(X\xrightarrow{f}Y\xrightarrow{g}Z\)、\(h=g\circ f\)と書くこともある。
合成写像の性質として、「定義域と終域が適切であれば、どの順番で合成しても写像は同じ」というものがある。
これを証明してみよう。
\(f:X\to Y\)、\(g:Y\to Z\)、\(h:Z\to W\)を写像とする。 このとき、 $$h\circ(g\circ f)=(h\circ g)\circ f$$ が成り立つ。
この定理の証明はさほど難しくないので、是非挑戦してみてほしい。
証明の流れを説明する。
- (ステップ1.) \(h\circ(g\circ f)\)と\((h\circ g)\circ f\)の定義域と終域が一致することを示す。
- (ステップ2.) 任意の\(x\in X\)に対して、\((h\circ(g\circ f))(x)=((h\circ g)\circ f)(x)\)を示す。
そもそも写像が等しいとはこの2条件を満たすことだった。
では、証明に入ろう。
(証明)
(ステップ1.)
\(f:X\to Y\)、\(g:Y\to Z\)、\(h:Z\to W\)を写像とする。
このとき、\(g\circ f:X\to Z\)であるため、\(X\xrightarrow{f}Y\xrightarrow{g}Z\xrightarrow{h}W\)であるから、\(h\circ(g\circ f):X\to W\)である。
一方、\(h\circ g:Y\to W\)であるため、\(X\xrightarrow{f}Y\xrightarrow{g}Z\xrightarrow{h}W\)であるから、\((h\circ g)\circ f:X\to W\)である。
従って、\(h\circ(g\circ f)\)と\((h\circ g)\circ f\)の定義域と終域が一致する。
(ステップ2.)
任意の\(x\in X\)に対して、
$$(h\circ(g\circ f))(x)=h((g\circ f)(x))=h(g(f(x)))$$
であり、かつ
$$((h\circ g)\circ f)(x)=(h\circ g)(f(x))=h(g(f(x)))$$
である。
従って、任意の\(x\in X\)に対して、\((h\circ(g\circ f))(x)=((h\circ g)\circ f)(x)\)が成り立つ。
以上により、\(h\circ(g\circ f)=(h\circ g)\circ f\)が成り立つ。
(Q.E.D.)
結
今回は「合成写像って何?」ということを説明した。
合成写像は高校数学における合成関数に対応する概念である。
ある定義域と終域の間の写像と、その終域を定義域とする写像とを”つなげた”写像である。
次回は「単射、全射、全単射、逆写像」について解説する。
これは特別な性質を持つ写像のことを指す。
これらは解析学で関数を扱う際に非常に重要になってくる。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに、「集合・写像・論理ー数学の基本を学ぶ」の方が入門者にはオススメです!





コメントをする