本記事の内容
本記事は写像の具体例を述べる記事である。
本シリーズでは一応写像と関数を呼び分けているのだが、双方の例を述べる。
本記事は以下の(前回の)記事で説明した写像のイメージが分かっていると理解しやすいと思われるので、以下のリンクから前回の記事も合わせて参照してください。
また、論理と集合の初歩についても解説していますので、そちらも合わせて御覧ください。
※シリーズ化しておりますので、その一部を掲載しています。
写像ってどんなの?
先に「ある対象に対して、別の対象(同じ場合もある)と対応付けする規則」が写像である、と述べた。
写像の例をいくつか挙げてみる。
例1.(料理を食べるときに使う食器との対応規則)
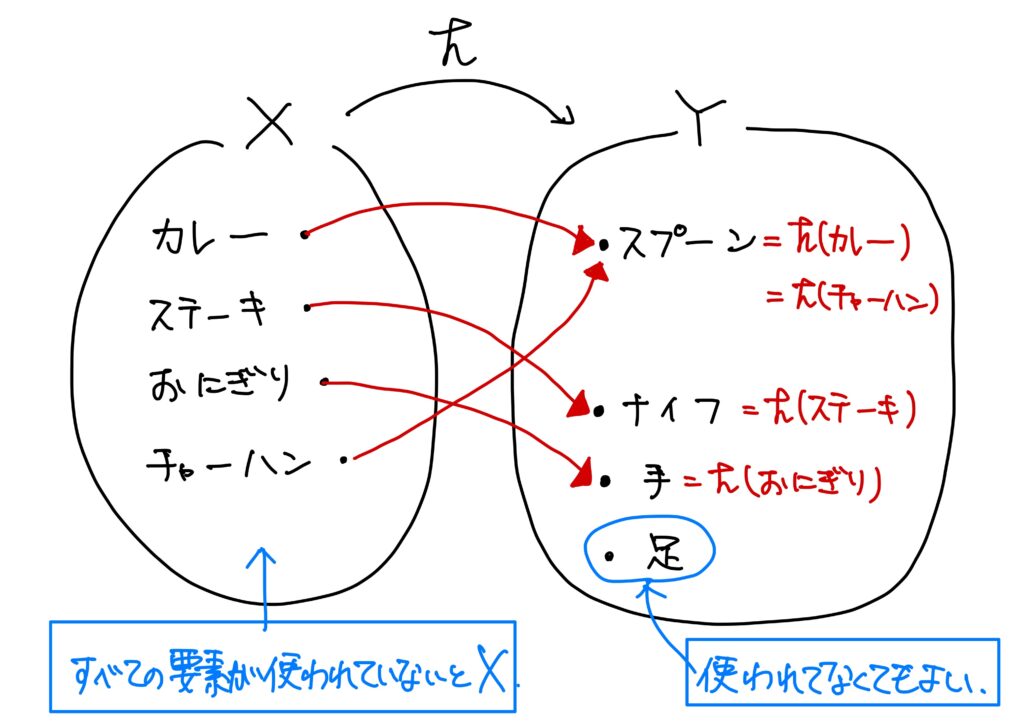
\(X=\{カレー,ステーキ、おにぎり,チャーハン\}\)、\(Y=\{スプーン,ナイフ,手,足\}\)とする。
このとき、カレーはスプーンで食べるため(手で食べる人もいるだろうが、日本人では極めて稀だと思うので排除している)、カレーとスプーンを対応させる。
同様にステーキはスプーンでは食べず、手で食べると熱い。
同様に足で食べる人もいない(見たことがない)。
ステーキはかじりつくのではなくナイフで切って小分けにして食べる。
故にステーキはナイフと対応させる。
おにぎりを食べるときにスプーン、ナイフ、足を使うことはないだろう(お上品な方は使うかもしれないが、筆者のような庶民には無縁)。
従って、おにぎりと手を対応させる。
チャーハンも同様にスプーンで食べるので、チャーハンとスプーンを対応させる。
この対応規則を\(h\)と書くとき、今述べた
- カレーとスプーン
- ステーキとナイフ
- おにぎりと手
- チャーハンとスプーン
という対応関係は、
- \(h(カレー)=スプーン\)、
- \(h(ステーキ)=ナイフ\)、
- \(h(おにぎり)=手\)、
- \(h(チャーハン)=スプーン\)
と書く。
すなわち、\(h(対応させたいモノ)=対応するモノ\)というわけである。
ここで3つ注意がある。
- \(X\)の要素に対して、対応するモノがただ1つに定まっていること。
- \(X\)の要素は全て使われていること。
- \(Y\)の要素はすべて使われている必要はない、ということ。
さらに、この例の特徴を述べておくと、
- \(X\)の別々の要素に対して、同じ\(Y\)の要素と対応しているものがある。
この対応規則\(h\)は\(X\)から\(Y\)への写像であるといい、\(h:X\to Y\)やら\(X\stackrel{h}{\to}Y\)と書く。
例2.(数学っぽい例)
\(X=\{1,2,3\}\)、\(Y=\{1,4,9\}\)とする。
\(X\)の要素\(1,2,3\)に対して\(Y\)の要素\(1,4,9\)を次のように対応させる。
- \(1\in X\)と\(1\in Y\)、
- \(2\in X\)と\(4\in Y\)、
- \(3\in X\)と\(9\in Y\)。
この対応規則を\(g\)と書く。
このとき、例1.の記法に則れば、
- \(g(1)=1\)、
- \(g(2)=4\)、
- \(g(3)=9\)。
である。
この例においても、
- \(X\)の要素に対して、対応するモノがただ1つに定まっていること。
- \(X\)の要素は全て使われていること。
- \(Y\)の要素はすべて使われている必要はない、ということ。(今回は全て使われている。)
を満たしている。
この対応規則\(g\)は\(X\)から\(Y\)への写像(この場合は関数と言っても良い)であり、\(g:X\to Y\)やら\(X\stackrel{g}{\to}Y\)と書く。

例3.(実数値の関数)
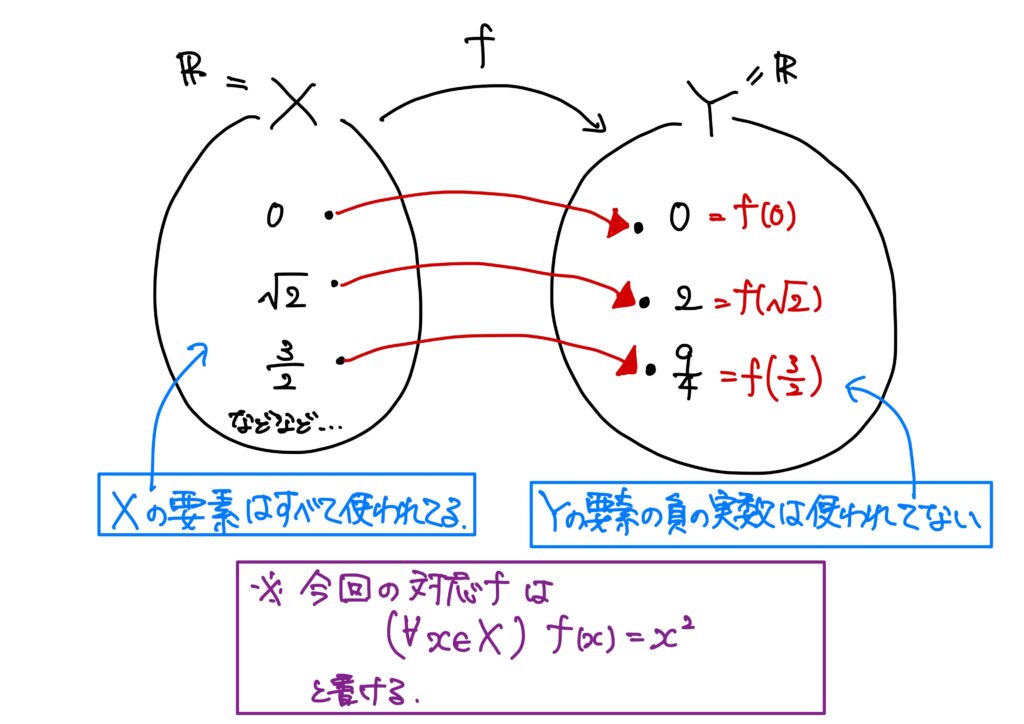
\(X=Y=\mathbb{R}\)とする。
このとき、任意の\(x\in X=\mathbb{R}\)に対して、\(Y=\mathbb{R}\)の要素\(y\)と\(x^2\)とを対応させる。
すなわち、任意の\(x\in X\)に対して、\(y\in Y\)を\(y=x^2\)で対応させる、と言っているわけである。
この記法は中学数学でも出現するため見慣れていると思われる。
例1.および例2.の記法に則れば、この対応規則\(f\)は
$$(\forall x\in X)\ f(x)=x^2$$
ということである。
この例においても、
- \(X\)の要素に対して、対応するモノがただ1つに定まっていること。
- \(X\)の要素は全て使われていること。
- \(Y\)の要素はすべて使われている必要はない、ということ。(今回は全て使われてはいない。\(Y\)の要素の負の実数には対応する\(X\)の要素がない。)
を満たしている。
この対応規則\(f\)は\(X=\mathbb{R}\)から\(Y=\mathbb{R}\)への写像であり、数に対しての対応規則なので関数と呼ぶ。
このとき、\(f:\mathbb{R}\to\mathbb{R}\)やら\(\mathbb{R}\stackrel{f}{\to}\mathbb{R}\)と書く。
この記法\(f(x)=x^2\)は高校数学で出現している。
この記法の意味は\(x\in\mathbb{R}\)に対して、\(x^2\in\mathbb{R}\)を対応させる規則が\(f\)ですよ、ということだったのだ。
結
今回は写像の例を挙げた。
前回は写像を「ある対象に対して、別の対象とを対応付けする規則」と述べた。
これは、今回の例で見た通り、「2つの集合の要素に対する対応関係」ということである。
ちなみに、例2および例3は数式的には同じ対応だと思える。
しかしながら、写像として、関数としては別物である。(後の記事で書きます。)
少々話がそれたが、写像は「2つの集合の要素に対する対応関係」なのだから、集合としては空集合でなければ何でも良い。
言ってしまえば、写像の集合の間の写像もあり得る。
写像は、どの集合の要素がどの集合の要素と対応しているという、ある種の”行き先(対応先)”を決めてあげれば、写像が決まる(写像は対応なのだから、どのように対応するかを決めてしまえば写像が決まるのは自然)。
次回は「数学的に写像って何?」ということを2つの立場から説明する。
例えば、「奇数の正体って何?」という質問には「正体は整数です。」と答える。
この例における”整数”に対応する対象を写像に対して述べる、ということである。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに、「集合・写像・論理ー数学の基本を学ぶ」の方が入門者にはオススメです!





コメントをする