本記事の内容
本記事は多変数有理関数が連続である、ということを説明する記事です。
本記事を読むにあたり、多変数多項式関数は連続である、ということについて知っている必要があるため、その際は以下の記事を参照してください。
多変数有理関数とは何かネ?
多変数有理関数は、一言で言えば、次です。
です。
多変数有理関数の説明の前に、1変数有理関数とは何だったかをチャラく復習します。
1変数有理関数のチャラい復習
1変数有理関数は\(\displaystyle f(x)=\frac{x^2+x+7}{x+5}\)のような形の関数のことを指すのでした。
数学的には以下でした。
\(P(x)\)および\(Q(x)\)を実係数多項式関数とする。 このとき、\(P(x)\neq0\)を満たす\(x\in\mathbb{R}\)に対して、 $$R(x)=\frac{Q(x)}{P(x)}$$ を実係数有理関数という。
ただし、多項式関数とは以下でした。
- 多項式 $$P(x)=\sum_{i=0}^{n}a_ix^i\quad(n\in\mathbb{N}\cup\{0\},\ a_i\in\mathbb{R})$$ の形の式を、\(x\)の実係数多項式(polynomial with real coefficients)という。
- 多項式関数 関数\(f:X\to Y\)が任意の\(x\in X\)で\(f(x)=P(x)\)を満たすとき、\(f\)は多項式関数という。 特に、\(P(x)\)が実係数多項式である場合、\(f\)を実係数多項式関数という。
詳しくは、【解析学の基礎シリーズ】関数の極限編 その8を御覧ください。
多変数有理関数は上記の多変数ver.です。
だったわけですので、多変数多項式関数をチャラく復習します。
多変数多項式関数のチャラい復習
\(n\)変数多項式関数は何だったかというと、次でした。
\(f\)が\(n\)変数の(\(\mathbb{R}\)上の)多項式関数であるとは、ある\(P(x_1,x_2,\dots,x_n)\in\mathbb{R}[x_1,x_2,\dots,x_n]\)が存在して、 $$ f:\mathbb{R}^n\to\mathbb{R},\quad f(x_1,x_2,\dots,x_n)=P(x_1,x_2,\dots,x_n)\quad ((x_1,x_2,\dots,x_n)^\top\in\mathbb{R}^n) $$ であることを言う。 ただし、$$ P(x_1,x_2,\dots,x_n)=\sum_{i_1=0}^N\sum_{i_2=0}^N\dots\sum_{i_n=0}^Na_{i_1i_2\cdots i_n}x_1^{i_0}x_2^{i_2}\cdots x_n^{i_n}\quad (N\in\mathbb{N},\ a_{i_1i_2\cdots i_n}\in\mathbb{R}) $$ をであり、また、多変数実係数多項式の全体の集合を $$ \mathbb{R}[x_1,x_2,\dots,x_n]=\left\{ P(x_1,x_2,\dots,x_n)\middle| N\in\mathbb{N},\ a_{i_1i_2\cdots i_n}\in\mathbb{R}\ (0\leq i_1,i_2,\dots,i_n\leq N)\right\} $$ で表す。
詳しくは【解析学の基礎シリーズ】多変数関数編 その12を御覧ください。
次に多変数有理式について話します。
多変数有理式
\(\displaystyle R(x,y)=\frac{x^2+2xy+3y^2+4x+5y+6}{7x+8y+9}\)のように、分母と分子が2変数\( x,y\)の実係数多項式であるような式を、変数\(x,y\)の実係数有理式と呼びます。
これは2変数の場合です。
2変数の場合を数学的に表すと、変数\(x,y\)の実係数有理式は
$$
R(x,y)=\frac{Q(x,y)}{P(x,y)}\quad (P(x,y),\ Q(x,y)\in\mathbb{R}[x,y],\ P(x,y)\neq 0)
$$
です。
では、多変数の有理式について説明します。
とはいえ、先程は\(x\)と\(y\)が変数でしたが、その変数の部分が\(x_1,x_2,\dots,x_n\)となるだけです。
\(P(x_1,x_2,\dots,x_n),\ Q(x_1,x_2,\dots,x_n)\in\mathbb{R}[x_1,x_2,\dots,x_n]\)とする。 このとき、\(P(x)\neq0\)を満たす\((x_1,x_2,\dots,x_n)\in\mathbb{R}^n\)に対して、 $$R(x_1,x_2,\dots,x_n)=\frac{Q(x_1,x_2,\dots,x_n)}{P(x_1,x_2,\dots,x_n)}$$ を変数\(x_1,x_2,\dots,x_n\)の多変数実係数有理式という。 ただし、 $$ \mathbb{R}[x_1,x_2,\dots,x_n]=\left\{ P(x_1,x_2,\dots,x_n)\middle| N\in\mathbb{N},\ a_{i_1i_2\cdots i_n}\in\mathbb{R}\ (0\leq i_1,i_2,\dots,i_n\leq N)\right\} $$ である。 また、多変数実係数有理式の全体の集合を $$ \mathbb{R}(x_1,x_2,\dots,x_n)=\left\{ \frac{Q(x_1,x_2,\dots,x_n)}{P(x_1,x_2,\dots,x_n)}\middle|P(x_1,x_2,\dots,x_n)\in \mathbb{R}[x_1,x_2,\dots,x_n],\\ Q(x_1,x_2,\dots,x_n)\in \mathbb{R}[x_1,x_2,\dots,x_n],\ P(x_1,x_2,\dots,x_n)\neq0 \right\} $$ で表す。
数式にすると少々複雑に見えるかもしれませんが、結局の所、多変数多項式を割り算しただけです。
余談(読み飛ばしてOK)
実は、\(\mathbb{R}(x_1,x_2,\dots,x_n)\)には体の構造が入るので、\(\mathbb{R}(x_1,x_2,\dots,x_n)\)は有理関数体とも呼ばれます。
体というのは、サラッと言うと「加減乗除ができる集合」のことです。
環と違って割り算もできる、というわけです。
ちなみに\(\mathbb{R}\)は加減乗除ができるので、体です。
「\(0\)では割れなくね?」と思うかもしれませんが、そもそも体は\(0\)で割る操作を排除しています。
多変数有理関数
多変数有理関数というのは、要するに\(\mathbb{R}(x_1,x_2,\dots,x_n)\)の要素の形の関数のことです。
これを数学的に書くと、次です。
\(f\)が\(n\)変数の(\(\mathbb{R}\)上の)多項式関数であるとは、ある\(P(x_1,x_2,\dots,x_n),\ Q(x_1,x_2,\dots,x_n)\in\mathbb{R}(x_1,x_2,\dots,x_n)\)が存在して、 $$ \Omega=\left\{ (x_1,x_2,\dots,x_n)\in\mathbb{R}^n\middle|P(x_1,x_2,\dots,x_n)\neq0 \right\} $$ としたとき、 $$ f:\Omega\to\mathbb{R},\quad f(x_1,x_2,\dots,x_n)=\frac{Q(x_1,x_2,\dots,x_n)}{P(x_1,x_2,\dots,x_n)}\quad ((x_1,x_2,\dots,x_n)^\top\in\Omega) $$ であることを言う。
とどのつまり、
$$
f(x_1,x_2,\dots,x_n)=\frac{\displaystyle\sum_{i_1=0}^N\sum_{i_2=0}^N\dots\sum_{i_n=0}^Na_{i_1i_2\cdots i_n}x_1^{i_0}x_2^{i_2}\cdots x_n^{i_n}}{\displaystyle\sum_{i_1=0}^N\sum_{i_2=0}^N\dots\sum_{i_n=0}^Nb_{i_1i_2\cdots i_n}x_1^{i_0}x_2^{i_2}\cdots x_n^{i_n}}\quad (N\in\mathbb{N},\ a_{i_1i_2\cdots i_n},\ b_{i_1i_2\cdots i_n}\in\mathbb{R})
$$
というときに、\(f\)は\(x_1,x_2,\dots,x_n\)を変数とする\(n\)変数(実係数)有理関数という、というわけです。
ただし、
$$
\sum_{i_1=0}^N\sum_{i_2=0}^N\dots\sum_{i_n=0}^Nb_{i_1i_2\cdots i_n}x_1^{i_0}x_2^{i_2}\cdots x_n^{i_n}\neq0
$$
です。
若干複雑ですが、\(n\)変数有理関数がどんなグラフかの例を挙げます。
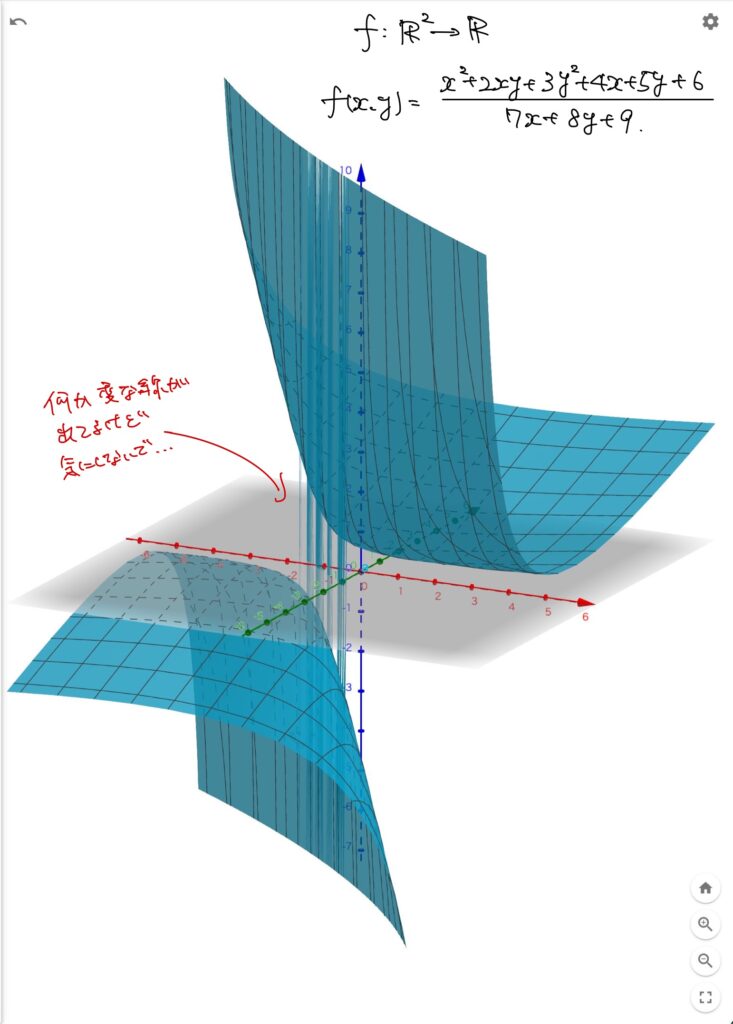
\(n\)変数有理関数は定義域で連続な関数である。
\(n\)変数有理関数は定義域で連続な関数です。
これは実は今まで証明した事実を用いることで証明が簡単にできます。
- (定理1.):連続な実数値関数の商は、分母が0でないような領域で連続である。
- (定理2.):\(n\)変数多項式関数は\(\mathbb{R}^n\)で連続な関数である。
という事実から簡単に証明できます。
具体的には、次です。
- \(\boldsymbol{a}\in\Omega\)とし、\(f\)と\(g\)は\(\boldsymbol{a}\)で連続とするとき、\(\displaystyle\frac{f(\boldsymbol{x})}{g(\boldsymbol{x})}\)は\(\boldsymbol{a}\)で連続である。すなわち、 $$ \lim_{\boldsymbol{x}\to\boldsymbol{a}}\frac{f(\boldsymbol{x})}{g(\boldsymbol{x})}=\frac{f(\boldsymbol{a})}{g(\boldsymbol{a})} $$ が成り立つ。
- \(f\)と\(g\)は\(\Omega\)で連続とするとき、\(\displaystyle\frac{f(\boldsymbol{x})}{g(\boldsymbol{x})}\)は\(\Omega\)で連続である。すなわち、 $$(\forall \boldsymbol{a}\in\Omega)\quad\lim_{\boldsymbol{x}\to\boldsymbol{a}}\frac{f(\boldsymbol{x})}{g(\boldsymbol{x})}=\frac{f(\boldsymbol{a})}{g(\boldsymbol{a})}$$ が成り立つ。
この定理の証明は【解析学の基礎シリーズ】多変数関数編 その6の多変数ベクトル値関数と実数値関数の商の極限の成分に着目すればよいので、既に証明しています。
この定理の証明は、【解析学の基礎シリーズ】多変数関数編 その12を御覧ください。
では、主張を明示してしまいましょう。
証明
証明といっても、定理1.と定理2.からわかる、というだけです。
というのも、定理2.から\(n\)変数実係数多項式関数は\(\mathbb{R}^n\)で連続です。
また、定理1.から、連続な実数値関数の商は、分母が0でないような領域で連続です。
多変数有理関数は、\(n\)変数実係数多項式関数の商ですので、多変数有理関数の分母が\(0\)でない領域(すなわち定義域)で連続です。
証明終わり
本当に成り立つのかネ?
例3. \(f:\Omega=\{(x,y)\in\mathbb{R}^2\mid x+y\neq0\}\to\mathbb{R}\)が\(\displaystyle f(x,y)=\frac{x}{x+y}\)で定めれているとします。このとき、\(f\)は\(\Omega\)で連続です。
証明
示したいことは、\(\boldsymbol{a}=(a,b)\)と書いたとき、
$$(\forall \boldsymbol{a}=(a,b)\in\Omega)(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall\boldsymbol{x}\in\Omega;\ 0<|(x,y)-(a,b)|<\delta\Rightarrow \left|\frac{x}{x+y}-\frac{a}{a+b}\right|<\epsilon)$$
です。
\(\delta>0\)を見つけるために式変形します。
もし上記を満たすような\(\delta>\)があったとすると、\(0<|\boldsymbol{x}-\boldsymbol{a}|=\sqrt{(x-a)^2+(y-b)^2}<\delta\)を満たす任意の\((x,y)\in\Omega\)に対して、
\begin{eqnarray}
\left|\frac{x}{x+y}-\frac{a}{a+b}\right|&=&\frac{1}{|a+b|}\cdot\left|\frac{(a+b)x-a(x+y)}{x+y}\right|\\
&=&\frac{1}{|a+b|}\cdot\frac{bx-ay}{|x+y|}
\end{eqnarray}
です。
ここで、\(g:\Omega\to\mathbb{R}\)を\(g(x,y)=x+y\)で定めるとすると、\(g(x,y)\)は任意の\(\boldsymbol{a}\)に対して\(\boldsymbol{x}\to\boldsymbol{a}\)のときに\(g(a,b)\)に収束します。
従って、ある\(\delta_0>0\)が存在して、\(0<|\boldsymbol{x}-\boldsymbol{a}|<\delta_0\)を満たす任意の\(\boldsymbol{x}\in\Omega\)に対して、下に有界です。
実際、次が成り立つからです。
この事実の証明は【解析学の基礎シリーズ】多変数関数編 その6を御覧ください。
従って、\(g(x,y)\)は\(0<|\boldsymbol{x}-\boldsymbol{a}|<\delta_0\)を満たす任意の\(\boldsymbol{x}\in\Omega\)に対して下に有界ですので、ある\(L\in\mathbb{R}\)が存在して、\(L<|x+y|\)ですから、\(\displaystyle\frac{1}{|x+y|}<\frac{1}{L}\)です。
故に、
\begin{eqnarray}
\frac{1}{|a+b|}\cdot\frac{bx-ay}{|x+y|}&<&\frac{1}{|a+b|}\cdot\frac{1}{L}\cdot|bx-ay|\\
&=&\frac{1}{|a+b|}\cdot\frac{1}{L}\cdot|bx-ab-ay+ab|\\
&=&\frac{1}{|a+b|}\cdot\frac{1}{L}\cdot|b(x-a)+a(b-y)|\\
&\leq&\frac{1}{|a+b|}\cdot\frac{1}{L}\cdot\left(|b|\cdot|x-a|+|a|\cdot|b-y|\right)\\
\end{eqnarray}
です。
ここで、\(\sqrt{(x-a)^2+(y-b)^2}<\delta\)であり、かつ\((x-a)^2\geq0\)、\((y-b)^2\geq0\)だったわけですので、\(|x-a|<\delta\)かつ\(|y-b|<\delta\)です。
従って、
\begin{eqnarray}
\frac{1}{|a+b|}\cdot\frac{1}{L}\cdot\left(|b|\cdot|x-a|+|a|\cdot|b-y|\right)<\frac{1}{|a+b|}\cdot\frac{1}{L}\cdot\left(|b|\delta+|a|\delta\right)
\end{eqnarray}
故に、\(\displaystyle\frac{1}{|a+b|}\cdot\frac{1}{L}\cdot\left(|b|\delta+|a|\delta\right)=\epsilon\)を\(\delta\)について解けば良いことが分かります。
これを解くと、
$$
\delta=\frac{L|a+b|}{|a|+|b|}\epsilon
$$
です。
ただ、\(g(x,y)\)の有界性を用いていることに注意する必要があります。
従って、
$$
\delta=\min\left\{\delta_0,\ \frac{L|a+b|}{|a|+|b|}\epsilon\right\}
$$
とすれば良い事がわかります。
以上のことから、
$$
\delta=\min\left\{\delta_0,\ \frac{L|a+b|}{|a|+|b|}\epsilon\right\}
$$
としたとき、\(0<|\boldsymbol{x}-\boldsymbol{a}|<\delta\)を満たすような任意の\((x,y)\in\Omega\)に対して、
\begin{eqnarray}
\left|\frac{x}{x+y}-\frac{a}{a+b}\right|<\frac{|a|+|b|E}{L|a+b|}\delta=\frac{(|a|+|b|)}{L|a+b|}\cdot\frac{L|a+b|}{|a|+|b|}\epsilon=\epsilon
\end{eqnarray}
となるので、\(f\)は\(\Omega\)で連続です。
結
今回は、多変数有理関数が定義域で連続ということを説明し、証明しました。
これは多変数多項式関数が連続であることと、実数値関数の商が定義域で連続だという事実から直ちに分かるということでした。
次回は連続な多変数ベクトル値関数の合成関数もまた連続な関数であるということを証明します。
乞うご期待!質問、コメントなどお待ちしております!



コメントをする