本記事の内容
本記事は「積分とはなにか?」ということをイメージと共に解説する記事です。
本記事を読むにあたり、全微分について知っている必要があるので、以下の記事も合わせてご覧ください。
高校数学での積分
筆者の記憶だと、高校数学では積分は
と習った気がします。
これは間違いではありません。
特に高校数学で学んだ1変数の場合は微分積分学の基本定理が成り立つため、微分と積分は互いに逆演算だ、ということが分かります。
その後、積分の計算方法を学び、ある種応用的な話として区分求積法というものを習った気がします。
実は、大学数学、というより一般に数学における積分はこれとは逆の流れです。
そもそも、積分というものは区分求積法(のようなもの)で定められていて、それからいろいろな事実が導き出されます。
例えば、\(F\)を\(f\)の原始関数(覚えていない方は後で厳密に説明しますのでご安心を)とすると、
$$
\int_a^b f(x)\ dx=F(b)-F(a)
$$
と計算しなさい、と習ったと思います。
もっと具体的な例を述べれば、
$$
\int_1^2 x^2\ dx=\left[ \frac{1}{3}x^3\right]_1^2=\frac{8}{3}-\frac{1}{3}=\frac{7}{3}
$$
と計算しようね、と習ったと思います(筆者の記憶によると…)。
実は、なぜこの計算方法でよいのか、ということがこの積分編を読んでいただけると分かります。
また、高校数学では「積分は\(f\)と\(x\)軸で囲まれたところの面積ですよ」と習ったと思います。
これは正しいです。
なぜ正しいか、ということが本記事で分かります。
積分の意味
積分の意味を解説します。
微分と積分の関係をサラッと。
積分は微分と並んで解析学の最も重要な演算です。
さらに、「変化する量」をとらえるのになくてはならないものです。
しばしば積分は微分の逆演算として捉えられています(先述の通り)。
しかしながら、これは限定されて意味でしか正しくありません。
特に多変数関数では、導関数\(\boldsymbol{f}^\prime(\boldsymbol{x})\)は全微分の導関数なわけですので行列の風貌をしています。
積分の意味を考えてみる。
積分の意味を考えるために次のような例を考えてみましょう。
均一な密度を持つような物体は
という関係があります。
それでは密度\(m\)が位置\(x\)と共に変化するよう物体に対して、\(m\)を知っている状態で全質量\(M\)を求めるにはどうしたら良いでしょうか。
この問題は解決法が1つしかないわけではありませんが、次のように考えてみます。
簡単のために物体は直方体\(I\)の形(3次元の区間)として、\(I\)の各辺を有限個に分割することにより、\(I\)を小さな直方体\(I_1,I_2,\dots,I_n\)に分割します。
各\(I_k\)が十分小さくて、密度\(m(x)\)があまり激しく変化しない場合は、\(I_k\)の点\(x_k\)における密度の値\(m(x_k)\)で\(I_k\)における\(I\)の密度は近似できると考えられます。
従って、①から質量\(=\)密度\(\times\)体積なわけですので、\(I_k\)に含まれる\(I\)の1部分の質量\(M_k\)は、\(I_k\)の体積を\(v(I_k)\)で表したとき
$$
M_k=m(x_k)\times v(I_k)
$$
と書けます(近似できます)。
すなわち、これを全ての\(I_1,I_2,\dots,I_n\)であつめたもの
$$
\sum_{k=1}^nm(x_k)v(I_k)\cdots②
$$
が全質量\(M\)の近似値となります。
今、\(n\)個に分割しましたが、この分割をより細かく(つまり\(n\)をどんどん大きく)して、\(I_k\)の対角線の長さが\(0\)に収束するときに、適当な条件(例えば\(m\)が連続)が満たされれば、②は一定の値に収束することが証明されます。
この極限が\(m\)の\(I\)上の積分
$$
\int_Im(x)\ dx
$$
の正体で、全質量\(M\)を表しています。
このように細かく分割した上で、各部分で密度\(\times\)体積の和を作り、分割を細かくした極限を考える、というのが積分法の考え方なのです。
このように見ると、「微分」と「積分」というのは良い名付け方だなあ、と思います。
微分はその瞬間を知るためにどんどん細かく分ける(“微”細に”分”割する)もので、積分は、全体を知るために”分”けたものを”積”み上げるもの、だからです。
積分って数学的に何ですか?
では、イメージの話はここまでにして、数学的に積分を説明します。
勿論、先程述べた積分の意味を厳密に書く、という話です。
そのために、いくつか用語を定めます。
\(n\)次元体積、直径、分割
\(n\)次元体積、直径、分割
- \(n\)次元体積 1次元の有界閉区間\([a,b]=\{x\in\mathbb{R}|a\leq x\leq b\}\)に対し、\(b-a\)をその長さという。また2次元の有界閉区間\([a,b]\times[c,d]=\{(x,y)\in\mathbb{R}^2|a\leq x\leq b,\ c\leq y\leq d\}\)の面積を\((b-a)(d-c)\)で定める。一般に\(n\)次元の有界閉区間 \begin{eqnarray} I&=&[a_1,b_1]\times[a_2,b_2]\times\dots\times[a_n,b_n]\\ &=&\{\boldsymbol{x}=(x_1,x_2,\dots,x_n)\in\mathbb{R}^n|a_i\leq x_i\leq b_i\ (1\leq i\leq n)\} \end{eqnarray} の\(n\)次元体積\(v(I)\)を $$ v(I)=\prod_{i=1}^n(b_i-a_i) $$ で定める。
- 直径 \(n\)次元の有界閉区間\(I\)に対して、 $$ d(I)=\sup_{\boldsymbol{x},\boldsymbol{y}\in I}\left\|\boldsymbol{x}-\boldsymbol{y}\right\| $$ を\(I\)の直径と呼ぶ。またこれは対角線の長さ\(\left\|\boldsymbol{b}-\boldsymbol{a}\right\|\)に等しい。ただし、\(\boldsymbol{a}=(a_1,a_2,\dots,a_n)\)、\(\boldsymbol{b}=(b_1,b_2,\dots,b_n)\)である。
- 分割 1次元区間\(I\)の分割とは、内点を共有しない有限個の小区間の和集合として\(I\)を表すことをいう。この場合、一つの分割\(\Delta\)は小区間の端点 $$ a=x_0<x_1<\dots<x_n=b $$ を与えることによって定まる。このとき\(x_i\)のことをこの分割\(\Delta\)の分点という。このような\(I\)の分割全体の集合を\(\mathcal{D}=\mathcal{D}(I)\)と書く。ただし、\(a=b\)の場合には\(a\)を分点とする分割しか存在しない。
\(n\)区間\(I\)の分割\(\Delta\)とはその\(n\)この辺\([a_1,b_i]\ (1\leq i\leq n)\)の分割\(\Delta_i\)の和集合である。
「小難しいことを書いてるな…」と思うかもしれませんが、読んでみると大したことはありません。
単に、\(n\)次元体積は各次元の区間の長さの積で、直径は端点の距離で、分割は\(n\)次元区間を書く次元で分割したもの、という単にそれだけです。
幅(mesh)
さて、\(\Delta\)が\(\Delta_i\)により\([a_i,b_i]\)が\(m\)個の内点を共有しない小区間の和集合となるとすると、\(\Delta\)により\(I\)は内点を共有しない\(\displaystyle\prod_{i=1}^nm_i=m\)個の\(n\)次元区間の和集合となります。
この\(m\)個の小区間に適当な順番で番号をつけてそれを
$$
I_k:k\in K(\Delta)
$$
としましょう。
ここで、\(K(\Delta)\)は分割\(\Delta\)の小区間\(I_k\)につけた番号の集合です。
さて、このとき、
$$
v(I)=\sum_{k\in K(\Delta)}v(I_k)
$$
が成り立ちます。
また、\(I_k\)の直径(対角線の長さ)を\(d(I_k)\)とするとき、
$$
d(\Delta)=\max_{k\in K(\Delta)}d(I_l)
$$
として、\(d(\Delta)\)を分割\(\Delta\)の幅(mesh、メッシュ)といいます。
これをまとめると次です。
幅(mesh)
分割\(\Delta\)の小区間\(I_k\)の直径を\(d(I_k)\)としたとき、 $$ d(\Delta)=\max_{k\in K(\Delta)}d(I_l) $$ を分割\(\Delta\)の幅(mesh、メッシュ)という。リーマン和
これは本記事で最も重要と言っても良いかもしれません。
リーマン和
\(n\)次元有界閉区間\(I\)上で定められた実数値関数に対して、区間\(I\)の任意の分割\(\Delta\)に対し、\(\Delta\)により得られる各小区間\(I_k\ (k\in K(\Delta))\)の中から任意に1点\(\boldsymbol{\xi}_k\)(これを\(I_k\)の代表点という)を取って作った和 $$ s\left(f;\Delta;\boldsymbol{\xi} \right)=\sum_{k\in K(\Delta)}f\left( \boldsymbol{\xi}_k\right)v\left( I_k\right) $$ を\(f\)の\(\Delta\)に関するリーマン和(Riemann sums)という。これはまさにイントロで述べた「質量\(=\)密度\(\times\)体積」の形をしています。
密度の部分が\(f\)です。
さて、リーマン和が\(I_k\)のとり方によらず、\(d(\Delta)\to0\)(直径をどんどん小さくしていくとき)のときある実数に収束るるのであれば、その実数を積分といいます。
リーマン積分
先程述べたことを厳密に書きます。
\(n\)次元有界閉区間\(I\)上で定められた実数値関数に対して、区間\(I\)の任意の分割\(\Delta\)に対し、\(\Delta\)により得られる各小区間を\(I_k\ (k\in K(\Delta))\)とする。このとき、ある実数\(J\)が存在して、\(I_k\)の代表点\(\boldsymbol{\xi}_k\)の取り方によらず、 $$ \lim_{d(\Delta)\to0}s\left(f;\Delta;\boldsymbol{\xi} \right)\left(=\lim_{d(\Delta)\to0}\sum_{k\in K(\Delta)}f\left( \boldsymbol{\xi}_k\right)v\left( I_k\right)\right)=J $$ となるとき、\(f\)は\(I\)上で(リーマン)可積分であるといい、\(J\)を\(f\)の\(I\)上での(リーマン)積分という。そして、 $$ J=\int_If=\int_If(\boldsymbol{x})\ d\boldsymbol{x}=\int\dots\int_If(x_1,\dots,x_n)\ dx_1\cdots dx_n $$ などと書く。
これは、どんどん分割幅を小さくして、細かく細かく分割したときの極限をリーマン積分という、という話です。
さて、リーマン積分は極限を用いて定められました。
これを復習がてら論理式で書いてみると、以下です。
$$
(\forall \varepsilon>0)\ (\exists \delta>0)\ {\rm s.t.}\ \left( \forall \Delta\in\mathcal{D}\right)d(\Delta)<\delta\Longrightarrow \left|s\left(f;\Delta;\boldsymbol{\xi} \right)-J \right|<\varepsilon
$$
ちなみに、この\(J\)は存在するならばただ1つです。
実際、仮に
$$
\lim_{d(\Delta)\to0}s\left(f;\Delta;\boldsymbol{\xi} \right)=J=J^\prime
$$
だったとしましょう。
このとき、\(d(\Delta)<\delta\)となるような分割\(\Delta\)を一つ取ると、
\begin{eqnarray}
\left|J-J^\prime \right|&=& \left| J\color{red}{-s\left(f;\Delta;\boldsymbol{\xi} \right)+s\left(f;\Delta;\boldsymbol{\xi} \right)}-J^\prime\right|\\
&\leq&\left| J-s\left(f;\Delta;\boldsymbol{\xi} \right)\right|+\left|s\left(f;\Delta;\boldsymbol{\xi} \right)-J^\prime\right|<2\varepsilon
\end{eqnarray}
となって、\(\varepsilon>0\)は任意だからです。
リーマン積分の図形的解釈
色々式を列挙しましたが、式だけでは厳つくてイメージが湧きにくいと思います。
そこで、1次元と2次元の場合に限りですが、図形的解釈を説明します。
1次元の場合
例えば、\(n=1\)のときは以下の図に示す青い長方形の面積の和がリーマン和\(s\left(f;\Delta;\xi \right)\)です。
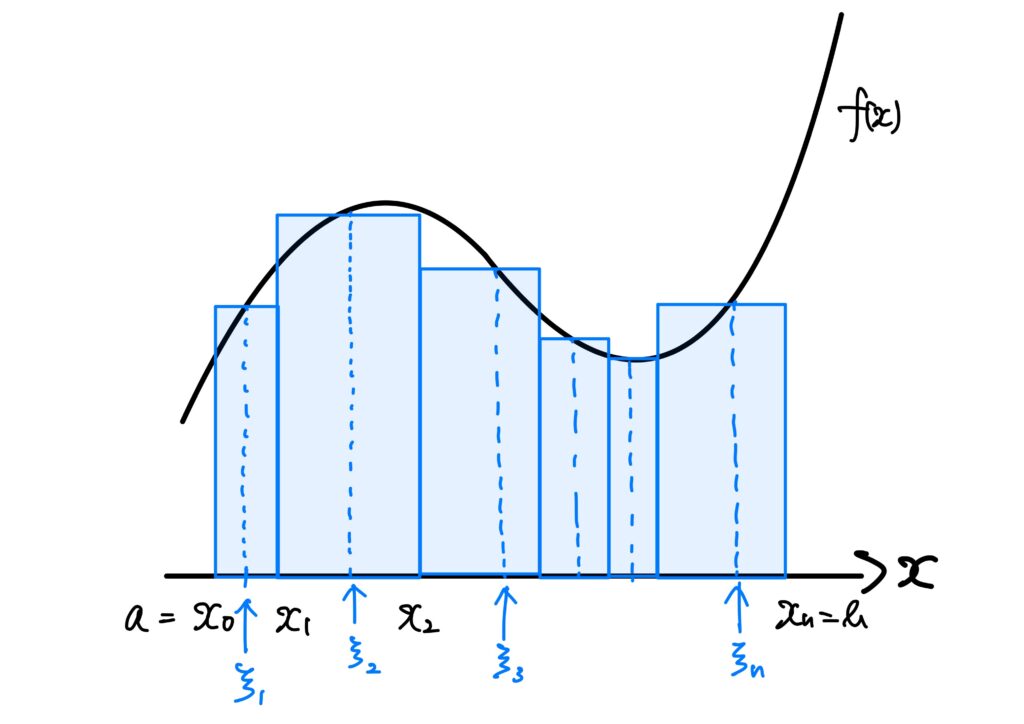
さらに、\(d(\Delta)\to0\)のとき、その極限である積分\(\displaystyle\int_If(x)\ dx\)が存在すれば、それは\(f\)のグラフと\(x\)軸で囲まれた集合の面積に他なりません。
従って、一般に図形の面積というのは積分を用いて定められています。
例えば、半径\(r\)の円の面積は\(\pi r^2\)ですが、これも積分を用いて定められています。
積分でもって面積を定めるのはまた後々の別記事で解説します。
2次元の場合
2次元の場合もなんてことありません。
単に、面積から体積に変わるだけです。
以下の図に示す青い直方体の面積の和がリーマン和\(s\left(f;\Delta;\boldsymbol{\xi} \right)\)です。

どんな関数が可積分なんですか?
可積分な関数はたくさんあります。
具体的な可積分な関数の積分は後の記事に回すとして、今回は最も簡単な例、定数関数が可積分であることを示してみます。
例1. \(I\subset\mathbb{R}\)、\(f:I\to\mathbb{R}\)を\(f(x)=c\)(定数)で定めます。
このとき、\(f\)は可積分で、
$$
\int_If(x)\ dx=cv(I)
$$
です。

実際、任意の\(I\)の分割\(\Delta\)に対して、
$$
s\left(f;\Delta;\xi \right)=\sum_{k\in K(\Delta)}cv(I_k)=c\sum_{k\in K(\Delta)}v(I_k)=cv(I)
$$
となるので、この式の両辺を\(d(\Delta)\to0\)とすると、
$$
\lim_{d(\Delta)\to0}s\left(f;\Delta;\xi \right)=\lim_{d(\Delta)\to0}cv(I)=cv(I)
$$
となります。
これままさに小学校で習った「長方形の面積\(=\)縦\((c)\times\)横\((v(I))\)」を表しています。
読者の皆様のコメントを下さい!
読者の皆様は中学校、高校の数学で躓いたことはありますか?
筆者はあります。
中学校のときに1度、高校のときには2度ありました。
中学校のときは1次関数で躓きました。
というより、関数というものが何かよく分からずに躓きましたので、2次関数でも躓きました。
高校のときは因数分解と極限で躓きました。
どの場合も勘所を掴むとスッと分かったのですが、その勘所を掴むまでに時間がかかりました。
恐らく、中高の数学の中で最も難しいのが関数の取り扱いではないか、と思っています。
それまでは”数字”という実態があるモノを扱ってきたのに対して、関数は”文字式”というある種実態が分かりにくいものを扱うからだと思っています。
中でも、高校数学の中では最も積分法が難しいと思います。
勿論、計算方法を覚えてしまう、という単にそれだけなら「覚えりゃいいんでしょ」ということで片付いてしまうわけですが、それだと計算はできるけれど論証はできません。
読者の皆様は中高の数学のどこで躓きましたか?
是非コメントで教えて下さい!
「躓いたことなど無い!」という方も是非コメントを下さい!
結
今回は、「積分とは何か?」ということを発想から説明しました。
今回は特になにか定理を証明する、というわけではありませんでしたが、今後の積分の話をする上での前提の話となってくるため、是非しっかり覚えてほしいです(ブックマークもしてね!)。
次回は積分の線形性と単調性について解説します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!




コメントをする