本記事の内容
本記事は前回(【解析学の基礎シリーズ】実数の連続性編 その18)で証明した「ある数列が収束することとコーシー列であることは同値」という命題からワイエルシュトラスの上限公理を証明する記事です。
本記事はコーシー列とワイエルシュトラスの上限公理を知っている必要になるため、以下の記事も合わせて御覧ください。
↓コーシー列の記事
↓ワイエルシュトラスの上限公理の記事
実数の連続性との関係は?
前回(【解析学の基礎シリーズ】実数の連続性編 その18)の記事で「数列が収束列であることとコーシー列であることは同値」ということが分かったので、コーシー列は収束列です。
つまり、コーシー列というのは
という直感に対応するので、実数の連続性と関係があります。
直感的でない言い方をすれば
が成り立つので、実数の連続性関係がある、ともいえます。
ここでは、「数列が収束列であることとコーシー列であることは同値」という真なる命題を「コーシーの収束条件」と呼ぶことにします。
では、定理を明示しましょう。

証明の流れを説明します。
- (ステップ1) 任意の\(b\in B\)と任意の\(c\in C\)との関係式を導出。
- (ステップ2) 先程の関係式を使って、単調増加数列と単調減少数列を作る。
- (ステップ3) 作った2つの数列が共にコーシー列であることを示す。
ここでアルキメデスの原理を使う。 - (ステップ4) 作った2つの数列が同じ値に収束することを示す。
コーシー列は収束するのだから、それぞれの収束先が一致することを示す。 - (ステップ5) その収束先が\(A\)の上限であることを示す。
定理6.の証明
何を示したいのかと言うと、ワイエルシュトラスの上限公理を示したいわけです。
ワイエルシュトラスの上限公理は何だったか、というと以下でした。
つまり、コーシーの収束条件とアルキメデスの原理を仮定したとき、\(A\subset\mathbb{R}\)が上に有界かつ空でないならば、\(\sup A\)が存在する、ということを証明したいわけです。
では証明に入ります。
(ステップ1)
\(A\subset\mathbb{R}\)が上に有界かつ空でないとします。
このとき、\(\sup A\)が存在することを示します。
\(A\)の上界の集合を\(B\)とし、\(C=B^c=\mathbb{R}\setminus B\)とします。
(※デデキントの定理\(\Rightarrow\)ワイエルシュトラスの上限公理を証明するときに似ている!)
\(A\)は上に有界なのだから、ある実数\(M\)が存在して、任意の\(a\in A\)に対して\(a\leq M\)です。
このとき\(M\)は\(A\)の上界なのだから、\(M\in B\)です。
従って、\(B\neq\emptyset\)です。
\(C=\mathbb{R}\setminus B\)であるので、\(\mathbb{R}\)から\(A\)の上界を取り除いた集合だから、\(C\)は\(A\)の上界でない実数の集合です。
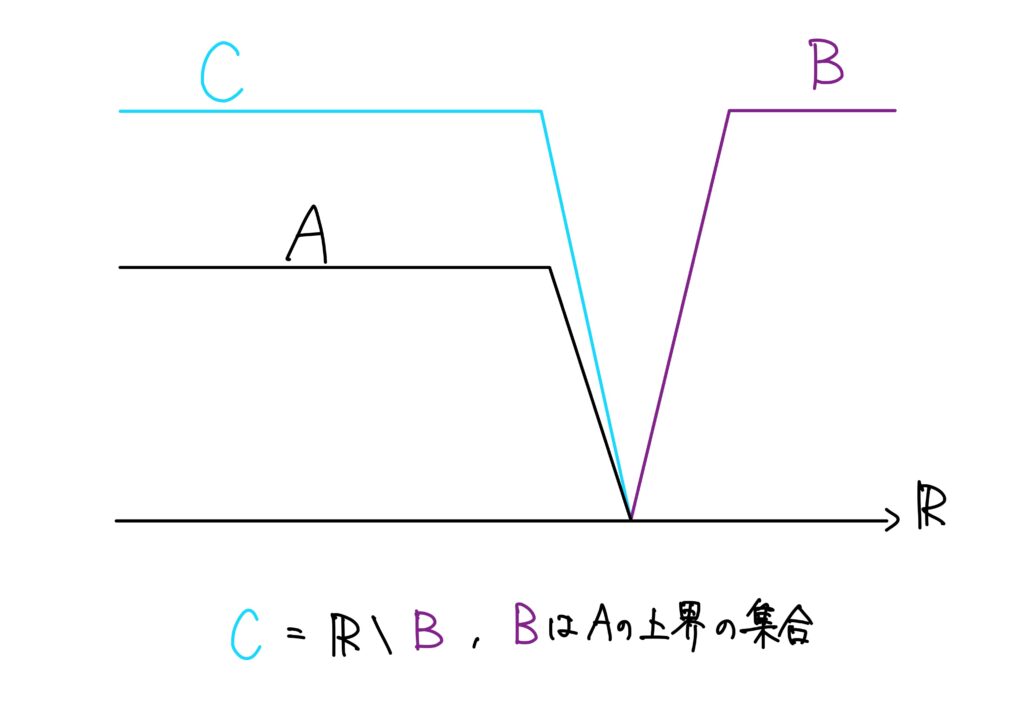
このとき、任意の\(b\in B\)と任意の\(c\in C\)に対して、ある\(a\in A\)が存在して、\(c<a\leq b\)が成り立ちます。
なぜならば、\(c\)は\(A\)の上界でないのだから、
$$(\forall c\in C)(\exists a_0\in A\ {\rm s.t.}\ a>c)$$
(※これは\(c\)が\(A\)の上界であることの否定!上界については【解析学の基礎シリーズ】実数の連続性編 その3を御覧ください)が成り立ちます。
すなわち、上記を満たすような\(a_0\in A\)を見つけてくることができます。
一方、\(B\)は\(A\)の上界の集合だったので、任意の\(b\in B\)は\(A\)の上界なのだから、任意の\(b\in b\)と任意の\(\alpha\in A\)に対して\(\alpha\leq b\)が成り立ちます。
これは任意の\(\alpha\in A\)で成り立つので、\(\alpha=a_0\)だったとしても成り立ちます。
従って、\(a\)として\(a_0\)を採用することで、任意の\(b\in B\)と任意の\(c\in C\)に対して、ある\(a\in A\)が存在して\(c<a\leq b\)が成り立ちます。
(ステップ2)
次に数列を作ります。
\(b_0\in B\)と\(c_0\in C\)を1つずつとり、以下のように帰納的に(順番に)数列\(\{b_n\}_{n\in\mathbb{N}}\)と\(\{c_n\}{n\in\mathbb{N}}\)を作ります。
- \(\displaystyle\frac{b_0+c_0}{2}\in B\)のとき、\(b_1=\displaystyle\frac{b_0+c_0}{2}\)、\(c_1=c_0\)とします。
- \(\displaystyle\frac{b_0+c_0}{2}\in C\)のとき、\(b_1=b_0\)、\(c_1=\displaystyle\frac{b_0+c_0}{2}\)とします。
同様にして、
- \(\displaystyle\frac{b_1+c_1}{2}\in B\)のとき、\(b_2=\displaystyle\frac{b_1+c_1}{2}\)、\(c_2=c_1\)、
- \(\displaystyle\frac{b_1+c_1}{2}\in c\)のとき、\(b_2=b_1\)、\(c_2=\displaystyle\frac{b_1+c_1}{2}\)
とします。
新たな記号を使って書けば、\(\displaystyle d_n=\frac{b_n+c_n}{2}\)としたとき、
- \(d_n\in B\)のとき、\(b_{n+1}=d_n\)、\(c_{n+1}=c_n\)とします。
- \(d_n\in C\)のとき、\(b_{n+1}=b_n\)、\(c_{n+1}=d_n\)とします。
このようにして、数列\(\{b_n\}_{n\in\mathbb{N}}\)と\(\{c_n\}{n\in\mathbb{N}}\)を作ります。
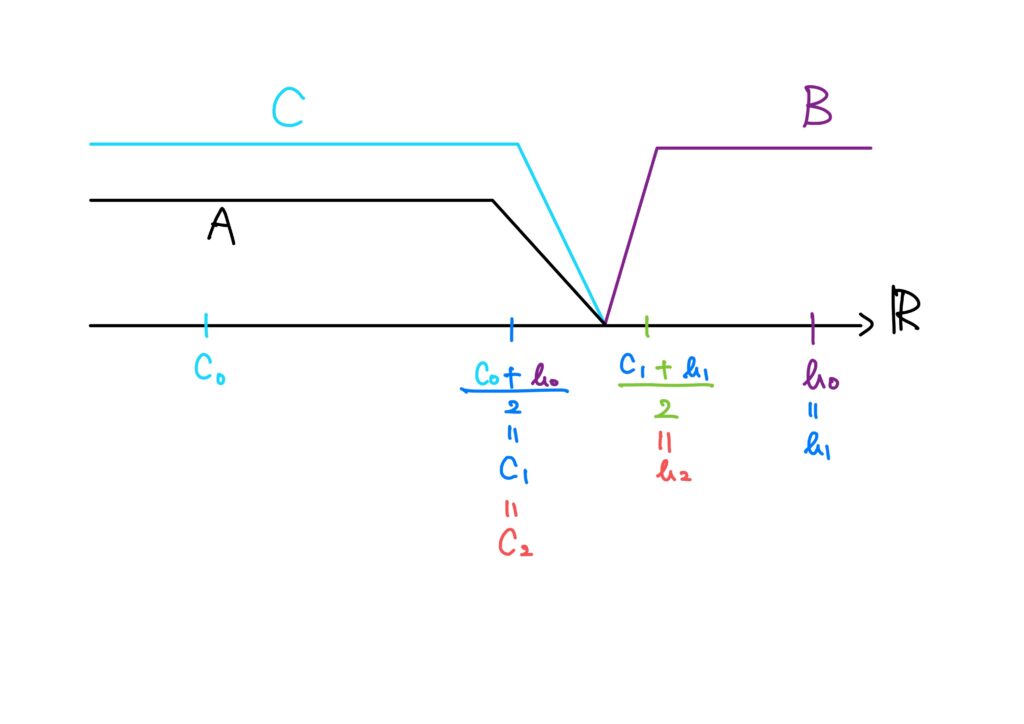
このとき、数列\(\{b_n\}_{n\in\mathbb{N}}\)は単調減少数列であり、数列\(\{c_n\}{n\in\mathbb{N}}\)は単調増加数列す。
実際、
$$b_{n+1}=\begin{cases}
b_n \\
\displaystyle\frac{b_n+c_n}{2}
\end{cases}
$$
なので、
$$b_{n+1}-b_n=\begin{cases}
b_n-b_n=0\leq 0 \\
\displaystyle\frac{b_n+c_n}{2}-b_n=\frac{c_n-b_n}{2}
\end{cases}
$$
です。
ここで、任意の\(b\in B\)と任意の\(c\in C\)に対して、ある\(a\in A\)が存在して、\(c<a\leq b\)が成り立ちます。
また、任意の\(n\in\mathbb{N}\)で\(c_n\in C\)かつ\(b_n\in B\)であるので、任意の\(n\in\mathbb{N}\)に対して\(c_n<b_n\)となるから\(c_n-b_n<0\)となります。
ゆえに数列\(\{b_n\}_{n\in\mathbb{N}}\)は単調減少数列です。
同様に
$$c_{n+1}=\begin{cases}
c_n \\
\displaystyle\frac{b_n+c_n}{2}
\end{cases}
$$
なのだから、
$$c_{n+1}-c_n=\begin{cases}
c_n-c_n=0\geq 0 \\
\displaystyle\frac{b_n+c_n}{2}-c_n=\frac{b_n-c_n}{2}
\end{cases}
$$
です。
ここで、任意の\(b\in B\)と任意の\(c\in C\)に対して、ある\(a\in A\)が存在して、\(c<a\leq b\)が成り立ちます。
また、任意の\(n\in\mathbb{N}\)で\(c_n\in C\)かつ\(b_n\in B\)であるので、任意の\(n\in\mathbb{N}\)に対して\(c_n0\)となります。
ゆえに数列\(\{c_n\}_{n\in\mathbb{N}}\)は単調増加数列です。
(ステップ3)
このとき、数列\(\{b_n\}_{n\in\mathbb{N}}\)および数列\(\{c_n\}_{n\in\mathbb{N}}\)はコーシー列です。
これを示すためにアルキメデスの原理を使います。
さて、数列\(\{b_n\}_{n\in\mathbb{N}}\)および数列\(\{c_n\}_{n\in\mathbb{N}}\)がコーシー列であることを示したいので、
$$(\forall \epsilon_1>0)(\exists N_1\in\mathbb{N}\ {\rm s.t.}\ \forall m,n\in\mathbb{N}\ m,n\geq N_1\Rightarrow |b_m-b_n|<\epsilon_1)$$
かつ
$$(\forall \epsilon_2>0)(\exists N_2\in\mathbb{N}\ {\rm s.t.}\ \forall m,n\in\mathbb{N}\ m,n\geq N_2\Rightarrow |c_m-c_n|<\epsilon_2)$$
であることを示したいわけです。
まずは
数列\(\{b_n\}_{n\in\mathbb{N}}\)について示します。
アルキメデスの原理を使います。
これは何だったかというと、
でした。
この事実の証明は【解析学の基礎シリーズ】実数の連続性編 その12を参照してください。
アルキメデスの原理において、\(a\)および\(b\)は任意の正の実数なのだから、\(a=\epsilon_1\)と書き直して、\(b=b_0-c_0\)としても成り立ちます。
従って、
$$(\forall \epsilon_1>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ b_0-c_0<N\epsilon)$$
が成り立ちます。
つまり\(\displaystyle\frac{b_0-c_0}{N}<\epsilon_1\)を満たすような自然数\(N\)を見つけてくることができます。
このとき、\(N_1\)として\(N\)を採用します。
\(k,l\in\mathbb{N}\)が\(k,l\geq N_1\)のとき、数列\(\{b_n\}_{n\in\mathbb{N}}\)は単調減少数列であるので、\(b{N_1}\geq b_k\)です。
従って、
$$|b_k-b_l|\leq |b_{N_1}-b_l|$$
です。
また、任意の\(n\in\mathbb{N}\)で\(b_n\leq c_n\)なのだから、
$$|b_{N_1}-b_l|\leq |b_{N_1}-c_{N_1}|$$
です。
さらに、任意の\(n\in\mathbb{N}\)で\(2^n>n\)(【解析学の基礎シリーズ】実数の連続性編 その12の補題7.の証明を参照してください)であり、\(\{b_n\}_{n\in\mathbb{N}}\)は単調減少数列、\(\{c_n\}_{n\in\mathbb{N}}\)は単調増加数列であることから、
$$|b_{N_1}-c_{N_1}|= \frac{b_0-c_0}{2^{N_1}}\leq\frac{b_0-c_0}{N_1}<\epsilon_1$$
が成り立ちます。
これをまとめて、\(k,l\in\mathbb{N}\)が\(k,l\geq N_1\)のとき、
$$|b_k-b_l|<\epsilon_1$$
が成り立ちます。
従って、数列\(\{b_n\}_{n\in\mathbb{N}}\)はコーシー列です。
同様にして、アルキメデスの原理において、\(a\)および\(b\)は任意の正の実数なのだから、\(a=\epsilon_2\)と書き直して、\(b=b_0-c_0\)としても成り立ちます。
従って、
$$(\forall \epsilon_2>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ b_0-c_0<N\epsilon)$$
が成り立ちます。
つまり\(\displaystyle\frac{b_0-c_0}{N}<\epsilon_2\)を満たすような自然数\(N\)を見つけてくることができます。
このとき、\(N_2\)として\(N\)を採用します。
\(k,l\in\mathbb{N}\)が\(k,l\geq N_2\)のとき、数列\(\{c_n\}_{n\in\mathbb{N}}\)は単調増加数列であるので、\(c_{N_1}\leq c_l\)です。
従って、
$$|c_k-c_l|\leq |c_k-c_{N_2}|$$
です。
また、任意の\(n\in\mathbb{N}\)で\(b_n\leq c_n\)なのだから、
$$|c_k-c_{N_2}|\leq |b_{N_2}-c_{N_2}|$$
です。
さらに、任意の\(n\in\mathbb{N}\)で\(2^n>n\)(【解析学の基礎シリーズ】実数の連続性編 その12の補題7.の証明を参照してください)であり、\(\{b_n\}_{n\in\mathbb{N}}\)は単調減少数列、\(\{c_n\}_{n\in\mathbb{N}}\)は単調増加数列であることから、
$$|b_{N_2}-c_{N_2}|= \frac{b_0-c_0}{2^{N_2}}\leq\frac{b_0-c_0}{N_2}<\epsilon_2$$
が成り立ちます。
これをまとめて、\(k,l\in\mathbb{N}\)が\(k,l\geq N_2\)のとき、
$$|c_k-c_l|<\epsilon_2$$
が成り立ちます。
従って、数列\(\{c_n\}_{n\in\mathbb{N}}\)はコーシー列です。
(ステップ4)
さて、「数列が収束列であることとコーシー列であることは同値」なのだから、\(\{b_n\}_{n\in\mathbb{N}}\)も\(\{c_n\}_{n\in\mathbb{N}}\)も収束します。
従って、
$$(\exists b\in\mathbb{R}\ {\rm s.t.}\ \lim_{n\to\infty}b_n=b)かつ(\exists c\in\mathbb{R}\ {\rm s.t.}\ \lim_{n\to\infty}c_n=c)$$
が成り立ちます。
つまり、\(\{b_n\}_{n\in\mathbb{N}}\)は\(b\in\mathbb{N}\)に、\(\{c_n\}_{n\in\mathbb{N}}\)は\(c\in\mathbb{R}\)に収束するとする、というわけです。
このとき、\(\displaystyle \lim_{n\to\infty}(b_n-c_n)\)を考えてみます。
もしこの極限が\(0\)であれば、\(b=c\)が成り立ちます。
実際、この極限は\(0\)です。
というのも、
$$\lim_{n\to\infty}(b_n-c_n)=\lim_{n\to\infty}\frac{b_0-c_0}{2^n}=0$$
だからである(【解析学の基礎シリーズ】実数の連続性編 その12の補題7.を参照してください)。
従って、\(b=c\)です。
このとき、\(\sup A=b=c\)であれば、証明は終わりです。
(ステップ5)
では最後に\(\sup A=b=c\)を証明します。
\(b=c\)であるから、\(\sup A=b\)を示せば良いです(勿論、\(\sup A=c\)を証明しても良い)。
\(\sup A=b\)、すなわち、\(b\)が\(A\)の上限であることを示したいので、次が示されれば良いです。
- \((\forall a\in A)a\leq b\),
- \((\forall \epsilon>0)(\exists a\in A)\ {\rm s.t.}\ a>b-\epsilon\)
まずは1.、すなわち\(b\)が\(A\)の上界である事を示します。
\(B\)は\(A\)の上界の集合なのだから、任意の\(n\in\mathbb{N}\)および任意の\(a\in A\)に対して、\(a\leq b_n\)です。
従って、\(\displaystyle \lim_{n\to\infty}a\leq\lim_{n\to\infty}b_n\)が成り立ちます。
故に\(a\leq b\)である(補題5.と【解析学の基礎シリーズ】実数の連続性編 その11の補題4.を参照してください)。
従って、任意の\(a\in A\)に対して、\(a\leq b\)なのだから、1.が示されました。
次に2.を示します。
今、\(\displaystyle \lim_{n\to\infty}c_n=b\)であるから、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |c_n-b|<\epsilon)$$
が成り立っています。
すなわち、\(n\geq N\)なる自然数\(n\)に対して\(|c_n-b|<\epsilon\)を満たすような番号\(N\)を見つけてくることができます。
従って、\(n\geq N\)なる\(n\in\mathbb{N}\)に対して\(-\epsilon<c_n-b<\epsilon\) であるので、\(n\geq N\)なる\(n\in\mathbb{N}\)に対して\(b-\epsilon<c_n\)です。
ここで、任意の\(n\in\mathbb{N}\)に対して、\(c_n\in C=\mathbb{R}\setminus B\)であるので、\(c_n\not\in B\)なのだから、\(c_n\)は\(A\)の上界ではありません。
従って、任意の\(n\in\mathbb{N}\)に対して、ある\(a\in A\)が存在して、\(c_n\leq a\)です(\(c_n\)が\(A\)の上界であることの否定!)。
これは任意の\(n\in\mathbb{N}\)で成り立っているのだから、先程見つけた\(N\)以上の自然数でも、つまり\(n\geq N\)であっても成り立ちます。
従って、\(n\geq N\)なる\(n\in\mathbb{N}\)に対して、\(c_n\leq a\)が成り立っています。
故に\(b-\epsilon<c_n\leq a\)が成り立ちます。
以上のことから\((\forall \epsilon>0)(\exists a\in A)\ {\rm s.t.}\ a>b-\epsilon\)が成り立つので、\(b\)は\(A\)の上限です。
定理6.の証明終わり
余談(読み飛ばしてOK。筆者の勘所)
上記の証明において、\(\{b_n\}_{n\in\mathbb{N}}\)と\(\{c_n\}_{n\in\mathbb{N}}\)コーシー列であることを示した部分がありました。
以前の記事でも少々述べたことだが、これはある番号を見つけてくるという証明です。
つまり、「〇〇が存在する。」ことの証明なのです。
証明ではサラッと「アルキメデスの原理を使います」なんて言っているのですが、筆者が最初に学んだときは「どうしてその発想に至ったのか」サッパリわかりませんでした。
「そりゃ確かにうまくいくけどさ。今までの証明の流れからしてアルキメデスの原理を使いそうだな、なんて思わなかったけど。」となりました。
そこで気がついたことを書いてみようかなと思います。
要は「どうやって見つけんだよ!」ということの一例を挙げるわけです。
証明の道中では
$$(\forall \epsilon_1>0)(\exists N_1\in\mathbb{N}\ {\rm s.t.}\ \forall m,n\in\mathbb{N}\ m,n\geq N_1\Rightarrow |b_m-b_n|<\epsilon_1)$$
を示したかったわけです。
つまり、上記を満たすような番号\(N_1\)を見つけたいわけです。
ここで一旦詰まるわけです。
そこで考え方をちょっと変えてみます。
「もし、そんな(上記を満たすような)\(N_1\)があったら…」 と考えるのです。
もし、そのような\(N_1\)があったならば、\(\{b_n\}_{n\in\mathbb{N}}\)は単調減少数列なので、\(k,l\geq N_1\)なる自然数\(k,l\)では\(b_k\leq b{N_1}\)かつ\(b_l\leq b_{N_1}\)です。
また、任意の\(b\in B\)および任意の\(c\in C\)に対して\(c<b\)です。
これを使えば、
$$|b_k-b_l|\leq |b_{N_1}-b_l|\leq|b_{N_1}-c_{N_1}|$$
を得ます。
\(|b_{N_1}-c_{N_1}|\)は区間\([c_{N_1},b_{N_1}]\)の長さなので、\(|b_{N_1}-c_{N_1}|=\displaystyle\frac{b_0-c_0}{2^{N_1}}\)です。
ここで、「これは前に\(0\)に収束することを示したな!」と思い至るわけです。
思い至らなくても、「\(\displaystyle\frac{b_0-a_0}{2^{N_1}}\)は\(0\)に収束するんじゃね?」と思えれば十分です。
すると、自然数\(n\)に対して、\(2^n>n\)なのだから、\(\displaystyle\frac{b_0-c_0}{2^{N_1}}<\frac{b_0-c_0}{N_1}\)です。
ということは、もし、任意の\(\epsilon>0\)に対して、\(\displaystyle\frac{b_0-c_0}{N_1}<\epsilon\)という\(N_1\)が見つけてこれれば、全て辻褄が合います。
ここでアルキメデスの原理が使える!と思い至るのです。
従って、
$$(\forall \epsilon_1>0)(\exists N_1\in\mathbb{N}\ {\rm s.t.}\ b_0-c_0<N_1\epsilon)$$
という\(N_1\)を取ればいいんだ!となるわけです。
その後に、ようやく証明を文字に起こすのです。
この話のミソとしては、
ということです。
数学をやってると、「論理的でなければならない!」という発想に至るかもしれません。
実は、筆者はそうでした。
つまり「もしそういう〇〇があったら…なんてやってしまったら勝手に仮定を追加する事になってしまって、主張としては別物になってしまうのではないか?」と抵抗がありました。
しかしながら、これは間違いだと今は思っています。
「もし〇〇があったら、どういうような展開になるのかな。」とまずは考えて探索し、その後本当に辻褄が合うのかを再度検討するのです。
このように考えるようになって、証明を考えるときに以前よりも時間がかからなくなり、理解しやすくなったと感じます。
結
今回は「ある数列が収束することとコーシー列であることは同値」という命題からワイエルシュトラスの上限公理を導出しました。
これにより、
- デデキントの定理
- ワイエルシュトラスの上限公理
- 有界な単調列は収束する。
- 区間縮小法+アルキメデスの原理
- ボルツァーノ-ワイエルシュトラスの定理
- コーシー列の収束
が同値であることをを間接的ではあるが、証明したことになります。
次回は論理と集合シリーズの新シーズンということで「写像」について説明します。
乞うご期待!質問、コメントなどお待ちしております!





コメントをする