「関数の連続の言い換え」〜片側極限〜【解析学の基礎シリーズ】関数の極限編 その６

本記事の内容

本記事は関数の連続を”片側極限”という別の言い方をする記事である。

本記事を読むにあたり、関数の連続、関数の収束について知っているとより理解が進むと思われるので、その際は以下の記事を参照してください。

「関数の収束って数学的に何？」「実際に証明してみよう！」【解析学の基礎シリーズ】関数の極限編 その２

本記事の内容本記事は関数の収束は数学的にどういうことかを説明し、実際に関数の収束を証明してみる記事である。本記事を読むにあたり数列の収束を理解し、関数の収束のイメージがついているとより理解しやすいと思われるので、その際は以下の記事を参照して

for-spring.com

「関数の連続って数学的に何？」「実際に証明してみよう！」【解析学の基礎シリーズ】関数の極限編 その５

...

for-spring.com

2022.04.05

関数の連続の言い換え

先に関数の連続は

のだった。
また、定義域のすべての要素$a$に対して上記が成り立つとき、定義域内で連続であるというのだった。
これらは結局関数$f$の極限が$f(a)$と一致するということだった。
直感的には$a$で関数がつながっているときに$a$で連続だ、ということだった。
これを言い換えてみると、

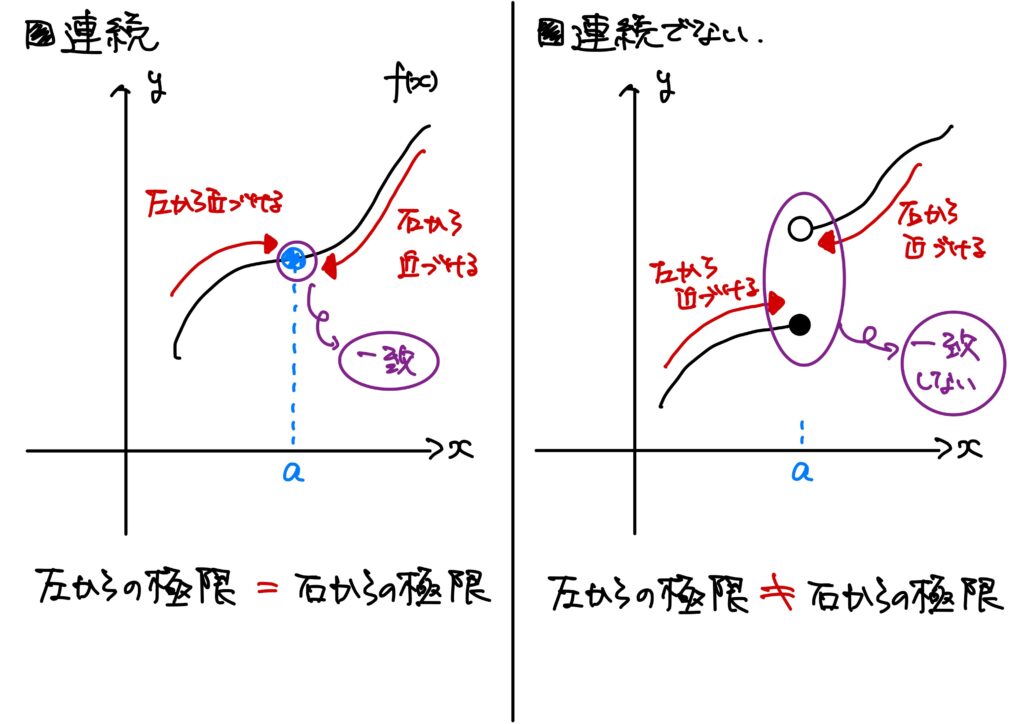
近づく方向ってどうやって数学で表現するの？

何ら難しいことではない。

• 右から近づく
  右から$a\in\mathbb{R}$に近づく、というのは$x$が$a$よりも大きい状態で$a$に近づくということ。
• 左から近づく
  左から$a\in\mathbb{R}$に近づく、というのは$x$が$a$よりも小さい状態で$a$に近づくということ。

なのである。
関数が$a$で連続であるというのは
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |f(x)-f(a)|<\epsilon)$$
が成り立つことだった。
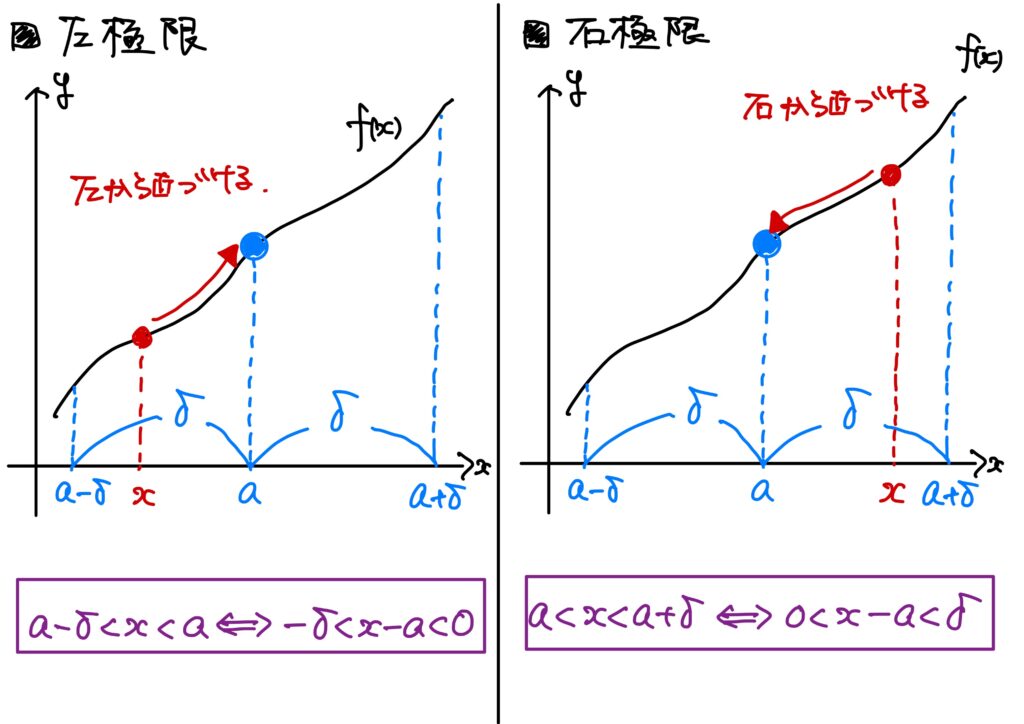
近づける方向は$x$に対する条件なのだから、$0<|x-a|<\delta$の部分を改変することで表現できる。 $0<|x-a|<\delta$は$-\delta$の状態で近づく。
従って、右から近づくことは$0<x-a<\delta$で表現される。
同様に、$-\delta<x-a<0$は左から近づくことを表現している。
これを論理式で書けば、次である。

片側極限と関数の連続との関係

では、片側極限がどのように関数の連続と関連するかということを表現する定理を述べる。

(証明)

$f:I\to\mathbb{R}$を関数、$\alpha\in\mathbb{R}$とする。

• $\displaystyle\lim_{x\to a}f(x)=\alpha\Rightarrow\lim_{x\to a+0}f(x)=\lim_{x\to a-0}f(x)=\alpha$の証明
  示したいことは、
  ①$\displaystyle(\forall \epsilon_1>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<x-a<\delta_1\Rightarrow |f(x)-\alpha|<\epsilon_1)$
  ②$\displaystyle(\forall \epsilon_2>0)(\exists \delta_2>0)\ {\rm s.t.}\ (\forall x\in I:\ -\delta_2<x-a<0\Rightarrow |f(x)-\alpha|<\epsilon_2)$
  が成り立つことである。
  $\displaystyle\lim_{x\to a}f(x)=\alpha$であるから、
  $$(\forall \epsilon_0>0)(\exists \delta_0>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta_0\Rightarrow |f(x)-\alpha|<\epsilon_0)$$
  が成り立つ。
  故に上記を満たす$\delta_0>0$を見つけてくることができる。
  $\delta_1$および$\delta_2$として$\delta$を採用し、$\epsilon_0>0$は任意だっため新たに$\epsilon$と書き換えると、$0<x-a<\delta$ならば、$0<|x-a|<\delta$が成り立つ。
  また、$-\delta<x-a<0$ならば、$0<|x-a|<\delta$が成り立つ。
  故に
  $$\displaystyle(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<x-a<\delta\Rightarrow |f(x)-\alpha|<\epsilon)$$
  かつ
  $$\displaystyle(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ -\delta<x-a<0\Rightarrow |f(x)-\alpha|<\epsilon_2)$$
  が成り立つので、①および②が成り立つ。

• $\displaystyle\lim_{x\to a+0}f(x)=\lim_{x\to a-0}f(x)=\alpha\Rightarrow\lim_{x\to a}f(x)=\alpha$の証明
  示したいことは、
  $$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |f(x)-\alpha|<\epsilon)$$
  である。
  今、$\displaystyle\lim_{x\to a+0}f(x)=\lim_{x\to a-0}f(x)=\alpha$なのだから、
  ①$\displaystyle(\forall \epsilon_1>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<x-a<\delta_1\Rightarrow |f(x)-\alpha|<\epsilon_1)$
  ②$\displaystyle(\forall \epsilon_2>0)(\exists \delta_2>0)\ {\rm s.t.}\ (\forall x\in I:\ -\delta_2<x-a<0\Rightarrow |f(x)-\alpha|<\epsilon_2)$
  が成り立っている。
  故に上記を満たす$\delta_1>0,\ \delta_2$を見つけてくることができる。
  $\delta$として、$\delta_1$と$\delta_2>0$の内、大きい方を採用し、$\epsilon_0>0$は任意だっため新たに$\epsilon$と書き換えると、
  ①’$\displaystyle(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<x-a<\delta\Rightarrow |f(x)-\alpha|<\epsilon)$
  ②’$\displaystyle(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ -\delta<x-a<0\Rightarrow |f(x)-\alpha|<\epsilon)$
  が成り立っている。
  従って、$0<|x-a|<\delta$ならば$0<x-a<\delta$かつ$-\delta<x-a<0$が成り立つ。
  故に
  $$\displaystyle(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |f(x)-\alpha|<\epsilon)$$
  が成り立つ。(Q.E.D.)

片側極限が一致するだけじゃだめなの？

だめなんです。
なぜならば、次の例を考えてみる。

例1.
$u:\mathbb{R}\to\mathbb{R}$が
$$u(x)=\begin{cases} x+2&(x\in\mathbb{R}\setminus \{1\})\\ 1&(x=1) \end{cases}$$
で定められていたとする。

このとき、$\displaystyle \lim_{x\to 1+0}u(x)=\lim_{x\to 1-0}u(x)=3$だが、$u(1)=1$である。
しかし、前回の記事(【解析学の基礎シリーズ】関数の極限編 その5)の例4.で証明したとおり、この$u$は$x=1$で連続でない。

結

今回は片側極限について解説した。

関数の連続は、要は「関数がつながっている」ということなのだから、「左から近づけたときと右から近づけたときの値が一致して、かつその値が関数の値とも一致しているとつながってるよね？」という比較的素朴な発想から来ている。

前回まで説明した関数の連続よりもむしろ分かりやすいかもしれない。

ただ、左右の極限が一致するだけでは連続とは言えないことに注意する。

次回は連続関数の和・差・積・商について説明する。

乞うご期待！質問、コメントなどお待ちしております！

この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください！
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ１冊持っておくと良いと思います！