本記事の内容
本記事は連続な関数の和・差・積・商もまた連続な関数であることを説明する記事である。
この記事を読むにあたり、関数の収束と連続を知っているとより理解が進むと思われるので、その際は以下の記事を参照してください。
連続関数の和・差・積・商
関数に対する「連続である」という条件は和をとっても差をとっても積をとっても割っても連続関数である。
「何の役に立つの?」と思うかもしれないが、筆者は非常に有用であると感じている。
筆者が挙げている例はどれも理解しやすいようなるべく明らかな例を挙げたりしているわけだが、実際に関数について考察するときは分かりやすいものばかりではない。
むしろわかりにくく複雑な関数のほうが多い。
そんなとき、その関数を細かく分けて個々が連続であれば全体も連続である、という事が分かるのである。
連続である事がわかると、後の記事で解説する中間値の定理や最大値の存在定理が使えることになり、より詳細な関数の特徴を捉えることができる。
本当にそうか?ということを和と差だけ確認してみる。
(※なぜ和と差だけなのか?というのは後述します。)
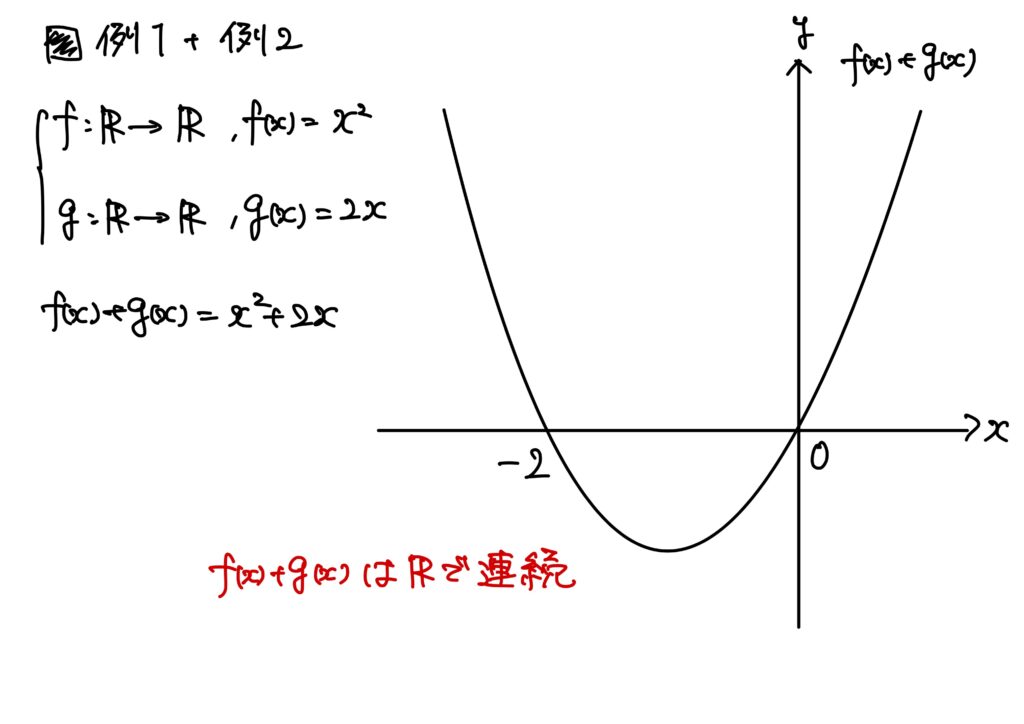
例1.+例2.
- 例1.:\(f:\mathbb{R}\to\mathbb{R}\)、\(f(x)=x^2\)
- 例2.:\(g:\mathbb{R}\to\mathbb{R}\)、\(g(x)=2x\)
とする。
このとき、\(f(x)+g(x)=x^2+2x\)である。
\(f(x)+g(x)\)は\(\mathbb{R}\)で連続である。
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |x^2+2x-a^2-2a|<\epsilon)$$
であれば良い。
任意の\(\epsilon>0\)に対して、\(\delta=-(|a|+1)+\sqrt{(|a|+1)^2+\epsilon}\)とすれば、\(\delta>0\)であり、
\begin{eqnarray}
|x^2+2x-a^2-2a|&=&|x^2-a^2+2(x-a)|\\
&=&|(x+a)(x-a)+2(x-a)|\\
&<&|x-a|(|x+a|+2)\\
&<&|x-a|(|x-a+2a|+2)\\
&\leq&|x-a|(|x+a|+2|a|+2)\\
&<&\delta(\delta +2|a|+2)\\
&=&\delta^2+2(|a|+1)\delta\\
&=&(|a|+1)^2-2(|a|+1)\sqrt{(|a|+1)^2+\epsilon}+(|a|+1)^2+\epsilon\\
&\quad&-2(|a|+1)^2+2(|a|+1)\sqrt{(|a|+1)^2+\epsilon}=\epsilon
\end{eqnarray}
であるから\(f(x)+g(x)\)は\(\mathbb{R}\)で連続である。
例1.-例2.
- 例1.:\(f:\mathbb{R}\to\mathbb{R}\)、\(f(x)=x^2\)
- 例2.:\(g:\mathbb{R}\to\mathbb{R}\)、\(g(x)=2x\)
とする。
このとき、\(f(x)-g(x)=x^2-2x\)である。
\(f(x)-g(x)\)は\(\mathbb{R}\)で連続である。

$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |x^2-2x-a^2+2a|<\epsilon)$$
であれば良い。
任意の\(\epsilon>0\)に対して、\(\delta=-(|a|-1)+\sqrt{(|a|-1)^2+\epsilon}\)とすれば、\(\delta>0\)であり、
\begin{eqnarray}
|x^2-2x-a^2+2a|&=&|x^2-a^2-2(x-a)|\\
&=&|(x+a)(x-a)-2(x-a)|\\
&<&|x-a|(|x+a|-2)\\
&<&|x-a|(|x-a+2a|-2)\\
&\leq&|x-a|(|x+a|+2|a|-2)\\
&<&\delta(\delta +2|a|-2)\\
&=&\delta^2+2(|a|-1)\delta\\
&=&(|a|-1)^2-2(|a|-1)\sqrt{(|a|-1)^2+\epsilon}+(|a|-1)^2+\epsilon\\
&\quad&-2(|a|-1)^2+2(|a|-1)\sqrt{(|a|-1)^2+\epsilon}=\epsilon
\end{eqnarray}
であるから\(f(x)-g(x)\)は\(\mathbb{R}\)で連続である。
このように、和と差については正しそうだ、という事が分かった。
実は、積、商についても成り立つ。
つまり、以下が成り立つ。
- \(a\in I\)とし、\(f\)と\(g\)は\(a\)で連続とするとき、次が成り立つ。
- \(f(x)+g(x)\)、\(f(x)-g(x)\)、\(f(x)g(x)\)は\(a\)で連続である。すなわち、
- \(\displaystyle \lim_{x\to a}(f(x)+g(x))=f(a)+g(a)\),
- \(\displaystyle \lim_{x\to a}(f(x)-g(x))=f(a)-g(a)\),
- \(\displaystyle \lim_{x\to a}(f(x)g(x))=f(a)g(a)\).
- \(\displaystyle g(a)\neq 0\)ならば、\(\dfrac{f(x)}{g(x)}\)は\(a\)で連続である。すなわち、 $$\lim_{x\to a}\dfrac{f(x)}{g(x)}=\dfrac{f(a)}{g(a)}$$ である。
- \(f(x)+g(x)\)、\(f(x)-g(x)\)、\(f(x)g(x)\)は\(a\)で連続である。すなわち、
- \(f\)と\(g\)は\(I\)で連続であるとするとき、次が成り立つ。
- \(f(x)+g(x)\)、\(f(x)-g(x)\)、\(f(x)g(x)\)は\(I\)で連続である。すなわち、
- \(\displaystyle(\forall a\in I) \lim_{x\to a}(f(x)+g(x))=f(a)+g(a)\),
- \(\displaystyle(\forall a\in I) \lim_{x\to a}(f(x)-g(x))=f(a)-g(a)\),
- \(\displaystyle(\forall a\in I) \lim_{x\to a}(f(x)g(x))=f(a)g(a)\).
- \(\displaystyle g(a)\neq 0\)ならば、\(\dfrac{f(x)}{g(x)}\)は\(I’=\{x\in\mid g(x)\neq 0\}\)で連続である。すなわち、 $$(\forall a\in I’)\ \lim_{x\to a}\dfrac{f(x)}{g(x)}=\dfrac{f(a)}{g(a)}$$ である。
- \(f(x)+g(x)\)、\(f(x)-g(x)\)、\(f(x)g(x)\)は\(I\)で連続である。すなわち、
実はこの定理はすでに証明している。
というのも、以下をすでに証明しているからである。
\(I\)を\(\mathbb{R}\)の区間、\(f:I\to\mathbb{R}\)および\(g:I\to\mathbb{R}\)を関数、\(a\in\bar{I}\)、\(A,b\in\mathbb{R}\)とし、\(\displaystyle \lim_{x\to a}f(x)=A\)、\(\displaystyle \lim_{x\to a}g(x)=B\)とする。 このとき、次が成り立つ。
- \(\displaystyle \lim_{x\to a}(f(x)+g(x))=\lim_{x\to a}f(x)+\lim_{x\to a}g(x)=A+B\),
- \(\displaystyle \lim_{x\to a}(f(x)-g(x))=\lim_{x\to a}f(x)-\lim_{x\to a}g(x)=A-B\),
- \(\displaystyle \lim_{x\to a}f(x)g(x)=\left(\lim_{x\to a}f(x)\right)\cdot\left(\lim_{x\to a}g(x)\right)=AB\),
- \(B\neq0\)ならば、\(\delta_0>0\)が存在して、\(|x-a|<\delta_0\)なる\(x\in I\)に対して、\(g(x)\neq 0\)で、\(\displaystyle \lim_{x\to a}\frac{f(x)}{g(x)}=\frac{\displaystyle\lim_{x\to a}f(x)}{\displaystyle\lim_{x\to a}g(x)}=\frac{A}{B}\)
この事実において、\(\forall a\in I\)に対して\(A=f(a)\)かつ\(B=g(a)\)のときを考えれば良いからである。
そういう意味で、積、商についての例を省いた。
この主張の証明は、【解析学の基礎シリーズ】関数の極限編 その3を参照してください。
結
今回は連続関数を四則演算で組み合わせた関数もまた連続関数であるということを説明した。
すなわち、連続な関数を和・差・積・商で組み合わせた関数は必ず連続である、ということである。
次回は合成関数、多項式関数、有理関数の連続について述べるために、多項式関数と有理関数とは何かを述べる。
乞うご期待!質問、コメントなどお待ちしております!
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ1冊持っておくと良いと思います!





コメントをする