本記事の内容
本記事はボルツァーノ-ワイエルシュトラスの定理のイメージを説明し、部分列とは?ということを説明する記事です。
実は、この定理は区間縮小法とアルキメデスの原理を用いて証明することができます。
証明は以下の記事を御覧ください。
ボルツァーノ-ワイエルシュトラスの定理の直感的な理解
一言で述べれば、
ということです。
少々厳密に言えば、「有界な数列には必ず収束するような一部の数列があります」ということです。
これは結局収束する数列を取ってこれると言っているわけなのだから、
という実数の連続性の直感に対応するのです。

部分列?一部の数列?
「一部の数列って何よ?」ということですが、これは部分列(subsequence)と呼ばれます。
例えば、以下のような数列です。
例1.
全ての自然数を小さい順に並べたものは数列となります。
記号で書けば、\(a_n=n\)としたときの\(\{a_n\}_{n\in\mathbb{N}}\)のことです。
この数列\(\{a_n\}_{n\in\mathbb{N}}\)に対して、奇数番目だけを選んでできた新たな数列\(\{b_n\}_{n\in\mathbb{N}}\)を考えます。
すなわち
$$b_1=a_1,\ b_2=a_3,\ b_3=a_5,\ \dots$$
として数列\(\{b_n\}_{n\in\mathbb{N}}\)を数列\(\{a_n\}_{n\in\mathbb{N}}\)の中から取ってくるわけです。
この数列\(\{b_n\}_{n\in\mathbb{N}}\)は数列\(\{a_n\}_{n\in\mathbb{N}}\)の部分列と呼ばれます。
この場合、数列\(\{b_n\}_{n\in\mathbb{N}}\)は数列\(\{a_n\}_{n\in\mathbb{N}}\)の要素を半分ほど捨てた、というわけです。
ただし、項の順番は変えない!
$$b_1=a_3,\ b_2=a_5,\ b_3=a_1,\ \dots$$
のようにはしません。
あくまで順番はそのままに一部を取ってきた。というわけです。
例2.
もっと変な選び方をしても勿論良いです。
例えば、例1.の数列\(\{a_n\}_{n\in\mathbb{N}}\)において、円周率\(\pi=3.1415926535…\)を使って選んだ数列\(\{c_n\}_{n\in\mathbb{N}}\)を考えます。
すなわち、
$$c_1=a_3,\ c_2=a_{31},\ c_3=a_{314},\ c_4=a_{3141}\dots$$
として数列\(\{c_n\}_{n\in\mathbb{N}}\)を数列\(\{a_n\}_{n\in\mathbb{N}}\)の中から取ってくるわけです。
この数列\(\{c_n\}_{n\in\mathbb{N}}\)も数列\(\{a_n\}_{n\in\mathbb{N}}\)の部分列と呼ばれます。
例1に比べて例2は盛大に捨てています。
ただし、項の順番は変えない!
$$c_1=a_{3141},\ c_2=a_{314},\ c_3=a_{31},\ \dots$$
のようにはしません。
あくまで順番はそのままに一部を取ってきた。というわけです。
この部分列を論理式で書けば、次です。
例1.においては\(n_k=2k-1\)、例2.においては\(n_1=3,\ n_2=31,\ n_3=314,\ n_4=3141,\dots\)としたわけです。
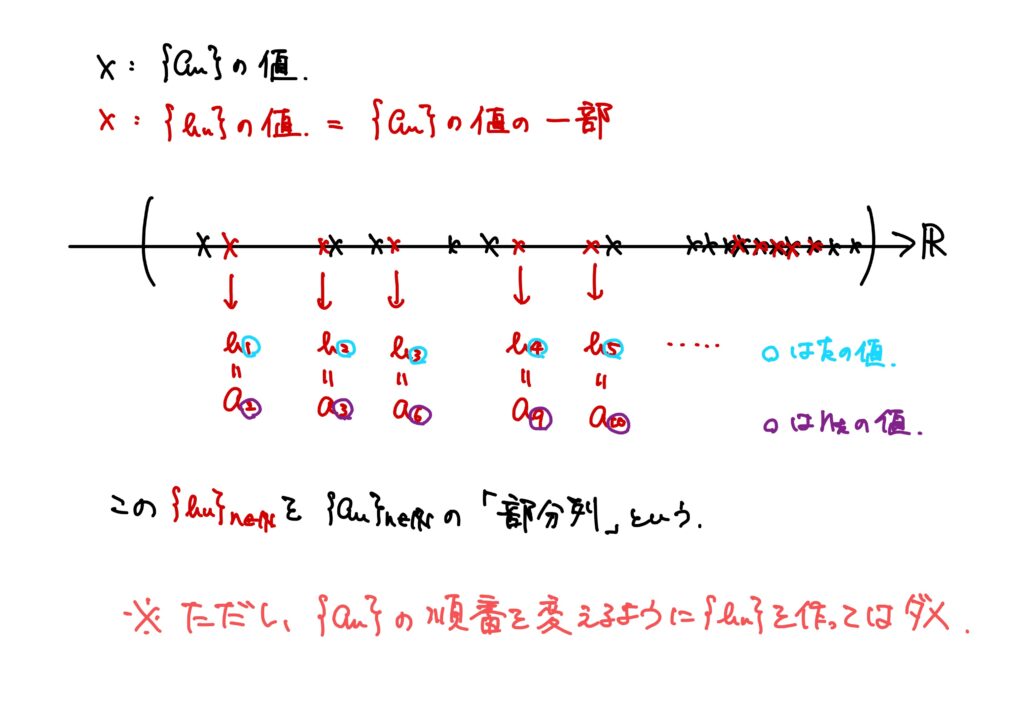
集合の言葉を使えば、\(\{a_n\}_{n\in\mathbb{N}}\)の列の順番を保つような\(\{a_n\mid n\in\mathbb{N}\}\)の部分集合の要素から得られる数列が部分列なのです。
結
今回は、Bolzano-Weierstrasの定理のイメージと部分列について説明しました。
この定理を一言で言えば、
ということで、数列が有界でありさえすれば、その中で必ず収束する数列を見つけ出せる、という主張です。
また、部分列というのは、もともとの数列の順番を変えずに一部分を取ってきて得られる数列のことを指します。
次回は「ボルツァーノ-ワイエルシュトラスの定理って本当に成り立つの?」です。
すなわち一例を出すということです。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする