本記事の内容
本記事は1変数の微分法の初歩、特に微分係数と導関数について解説する記事です。
本記事を読むにあたり、1変数実数値関数の極限について知っている必要があるため、その際は以下の記事を参照してください。
1変数実数値関数の微分編を読む前に
通常、1変数実数値関数の微分法は数Ⅱで学習するため、文系理系問わずに少なくとも1回は触れたことがあるはずです。
従って、この単元はエクストリームに復習する、ということを前提に話を進めます。
ただ、数Ⅲは主に理系のみが学習すると思われますので、数Ⅲの範囲については丁寧に行きます。
とはいえ、「これ知ってるよね?」というのはなるべく少なくして、「これだけ知ってればいいぜ!」という形式で進みます。
故に、「微分なんて覚えてねえぞ」という方についても読んで頂けます。
では行きましょう!
微分係数って?
微分係数は、平たく一言で言えば、
です。
少々数学的に言えば、ある瞬間の平均変化率です。
微分係数のイメージ
「平均変化率とは何かネ?」ということですが、簡単です。
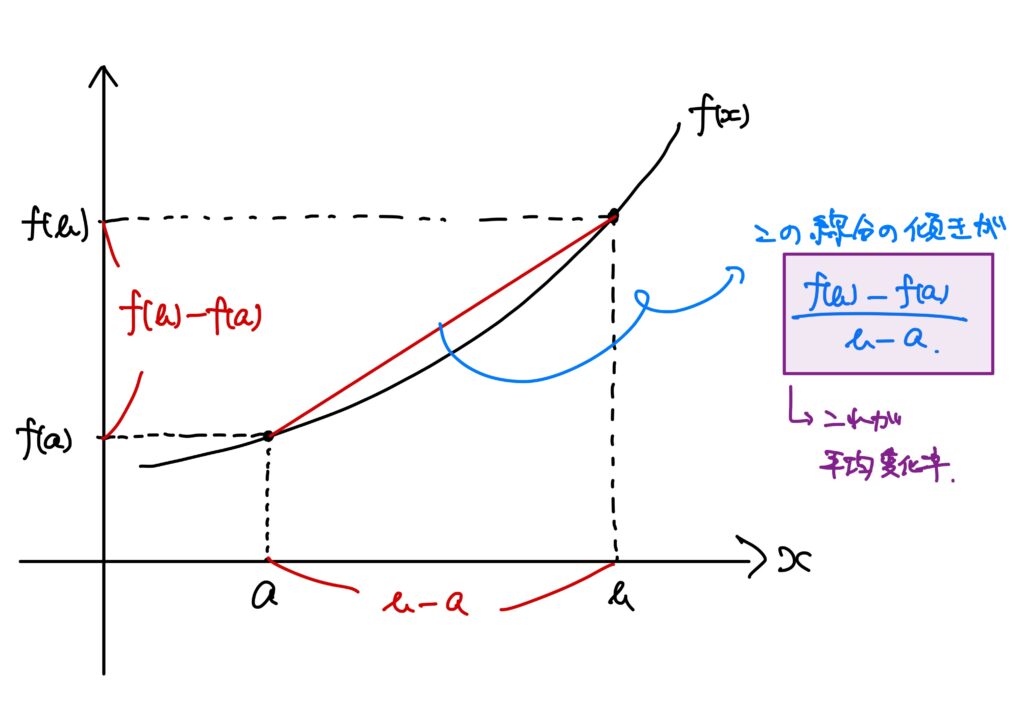
この平均変化率は\(a\)と\(b\)の間で、平均してどのくらい変化するかを表している量です。
さらに、\(\displaystyle\frac{f(b)-f(a)}{b-a}\)は\((a,f(a))\)と\((b,f(b))\)を結ぶ直線の傾きそのものだと言うことに注意してください。
さて、平均変化率に対応して、微分係数は、\(a\)という”瞬間”でどのくらい変化するかを表す量です。
では、”瞬間”はどのように表すことができるのか、というと極限で表すことができます。
今は\(a\)という瞬間でどのくらい変化するかを知りたいわけですので、\(a\)を固定して、\(b\)を\(a\)に近づけます。
従って、\(\displaystyle\lim_{b\to a}\frac{f(b)-f(a)}{b-a}\)が微分係数です。
この微分係数は「ある”瞬間”での変化量」ですので、\(f\)の\(x=a\)での接線の傾きを指します。

\(\displaystyle\lim_{b\to a}\frac{f(b)-f(a)}{b-a}\)を言い換えることができます。
\(h=b-a\)と置きます。
すると、\(b=a+h\)です。
従って、
$$
\frac{f(b)-f(a)}{b-a}=\frac{f(a+h)-f(a)}{h}
$$
です。
また、\(b\to a\)ということは、\(h\to 0\)ということですので、
$$
\lim_{b\to a}\frac{f(b)-f(a)}{b-a}=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}
$$
です。
微分係数は数学的に何かネ?
では、微分係数を数学的に述べます。
\(I=(a,b)\)を\(\mathbb{R}\)の開区間とし、\(f:I\to \mathbb{R}\)とする。 このとき、\(t\in I\)に対して $$ c=\lim_{h\to 0}\frac{f(t+h)-f(t)}{h} $$ という\(c\in \mathbb{R}\)が存在するとき、\(f\)は\(t\)で微分可能であるといい、\(c\)を\(f\)の導値、または微分係数という。このとき、 $$ c=f^\prime(t)=\frac{df}{dt}(t)=\frac{d}{dt}f(t)=\frac{df(t)}{dt}=\left(f(t)\right)^\prime=\left(Df\right)(t) $$ と書く。
要は、ある点\(x=t\)での接線の傾きが微分係数で、微分係数が存在するときに\(f\)は\(t\)で微分可能だという、というわけです。
導関数って?
微分係数が分かればなんてこと有りません。
導関数のイメージ
一言で言ってしまえば、
です。
\(f\)の接線はどの点でも同じわけではありません。
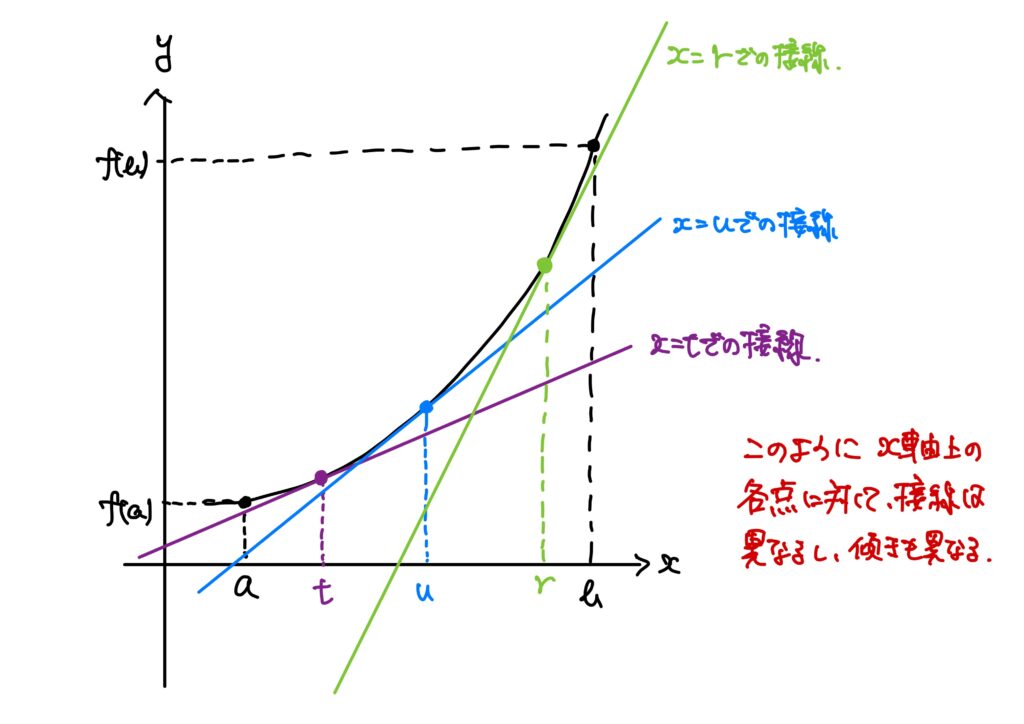
図のように、定義域の各点に対して接線は変わります。
従って、定義域の各点に対してその点の接線の傾きを対応させることができます。
この対応、すなわち関数が導関数です。
すごく平たく言えば、「ある点\(t\)の接線の傾きを\(t\)で表したもの」とも言えるかもしれません。
導関数は数学的に何かネ?
では、数学的に明示しましょう。
\(I=(a,b)\)を\(\mathbb{R}\)の開区間とし、\(f:I\to \mathbb{R}\)とする。 任意の\(t\in I\)に対して、\(f\)が微分可能であるとするとき、\(t\mapsto f^\prime(t)\)で定められる関数を導関数という。
導関数はあくまで微分係数の関数なのであって、微分係数ではありません。
ただ、導関数\(F\)の\(x=t\)での値\(F(t)\)は\(f\)の\(x=t\)での接線の傾きです。
例
簡単ではありますが、例を挙げます。
例1. \(f:(0,2)\to \mathbb{R}\)が\(f(x)=x^3\)で定められているとします。
このとき、\(x=1\)の微分係数\(f^\prime(1)\)と\(f\)の導関数を求めます。
$$
f^\prime(1)=\lim_{h\to 0}\frac{f(1+h)-f(1)}{h}=\lim_{h\to 0}\frac{3h+3h^2+h^3}{h}=\lim_{h\to 0}(3+3h+h^2)=3
$$
です。
導関数は
$$
f^\prime(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}=\lim_{h\to 0}\frac{3x^2h+3xh^2+h^3}{h}=\lim_{h\to 0}(3x^2+3xh+h^2)=3x^2
$$
です。
結
今回は微分可能、微分係数、導関数についてエクストリームに説明しました。
結局の所、平均変化率の極限を微分係数といい、その極限が存在するときに微分可能といいます。
また、微分係数はその点における接線の傾きを指します。
接線の傾きは店によって異なるため、関数をとして捉えることができます。
その関数を導関数と呼びましょう、ということです。
次回は、関数の和差積商の微分法の証明を行います。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする