真理値表とは？「かつ、または、ならば」とは？

基礎数学

2023.05.07 2022.01.23

本記事の内容
序
真理値表
「かつ」、「または」
同値および論理演算の諸性質
1. 同値
2. 論理演算の諸性質
ならば（含意）
余談
結

本記事の内容

　本記事は「数学の文章って何言ってるかわかんない」、「論理的ってどういうこと？」、「数学の勉強をしてみたいけど、何が書いてあるか読めない」という方向けである。
そういう方に向けて、「真理値表」および「かつ」、「または」、「ならば」を含む命題の真偽について解説する。

本記事は「命題の否定」を知っている必要があるため、ご存じない方は以下（前回の記事）をご参照ください。

「命題って？」となっている方は以下（前々回の記事）をご参照ください。

序

「かつ」、「または」、「ならば」という単語や言い回しは日常でも使うことがある。
論理の世界（特に数学）でも”ほぼ”同じ意味である。
従って、「そんなの知ってるよ」となるかもしれないが、特に「または」と「ならば」については日常とは異なる使い方をする場合があるので注意が必要である。

本記事で解説する「真理値表」、「かつ」、「または」、「ならば」および次回解説する述語論理を知っていれば、もう数学の文章を読めるようになる。
勿論、特有の記号が出現したりするため、記号に慣れるまでは多少時間がかかるかもしれないが、本質的にはこれらを理解することで数学の文章が読めるようになる。

さらに、本記事を読むことで、「命題とは？」【論理と集合シリーズ】数学の文章を読むための論理的思考の基礎　その１で挙げた命題の例

「クジラが爬虫類ならば日本国国会議事堂は２つ存在する。」

という命題の真偽が判定できるようになる。

真理値表

まずは真理値表について述べる。
これも簡単だが重要な概念である。
というのも、今後学ぶ「かつ」やら「または」やら「ならば」の真偽のルールを真理値表で決めるからである。

「真理値？」となっている方は前々回の記事（「命題とは？」【論理と集合シリーズ】数学の文章を読むための論理的思考の基礎　その１）をご参照ください。

さて、任意の命題$p$について、$\lnot p$の真理値は、$p$の真理値がTであればF、$p$の真理値がFであればTである（排中律と無矛盾律から）。
このことを次のように表形式で表したものを真理値表（truth table、真偽表）という。

$p$	$\lnot p$
T	F
F	T

表１：$p$とその否定$\lnot p$の真理値表

不要かもしれないが、行ごとに読む。$p$がTのとき$\lnot p$はF。$p$がFのとき$\lnot p$はT。

「かつ」、「または」

「かつ」、「または」は日常でも使うのだが、数学で使う論理にも出現する。
序で述べた通り「そんなの知ってるよ」となるかもしれないが、特に「または」については日常とは異なる使い方を持つため注意が必要である。

「かつ」（論理積）

　２つの命題$p$と$q$に対して、「$p$であり、かつ$q$である」という命題を$p\land q$と表し、「$p$かつ$q$」、「$p$ and $q$」と読む。
また、$p\land q$を$p$と$q$の論理積(logical conjunction)、連言（conjuction）という。
”連言”という言葉はあまり使われない。

ここで、$\land$という記号は数学において論理積以外でも使われる。
例えば、ウェッジ積が挙げられる。

ここでも、さも当然かのように「$p$および$q$が命題ならば$p\land q$も命題である。」が成り立つことを認めている。
「本当に？」と思う方は余談で”少しだけ”解説していますのでそこを参照ください。

「そして」やら「〜だし、〜」やらも「かつ」と同じ意味である。

$p\land q$の真理値を、すなわち真偽のルールを次の真理値表で決める。

$p$	$q$	$p\land q$
T	T	T
T	F	F
F	T	F
F	F	F

$p\land q$の真理値表

この表を一言で述べれば、「$p\land q$がTなのは$p$および$q$がともにTであるときのみ。」である。

または（論理和）

　２つの命題$p$と$q$に対して、「$p$であるか、または$q$である」という命題を$p\lor q$と表し、「$p$または$q$」、「$p$ or $q$」と読む。
また、$p\lor q$を$p$と$q$の論理和(logical disjunction)、選言（disjunction）という。
これも”選言”という言葉はあまり使われない。

またもや、さも当然かのように「$p$および$q$が命題ならば$p\lor q$も命題である。」が成り立つことを認めている。
「本当に？」と思う方は余談で少しだけ解説していますのでそこを参照ください。

日常で使うときの「または」に対応する言い回しは様々ある。
例えば、「〇〇か、△△」やら「もしくは」やら「あるいは」などがある。
これらは日常だけでなく論理の世界でも使われ、日常とは少々異なった使い方をする。
要は、日常で用いる「または」及びそれに準じた言い回しと、論理の世界で使う「または」は似て非なるものである、ということである。
※これについては言い回しについてで述べる。

$p\land q$の真理値を次の真理値表で定める。

$p$	$q$	$p\lor q$
T	T	T
T	F	T
F	T	T
F	F	F

$p\lor q$の真理値表

2,3,4行目に対しては抵抗が無いと思われるが、１行目、すなわち$p$がT、$q$がTであるとき、$p\lor q$がTである、というのは少々抵抗があるかもしれない。
日常で使う「または」は「いずれか一方が成り立つ」（片方だけが成り立ち、もう一方は成り立たない）という意味（排他的論理和(exclusive or)という）で使う場合もあるからである。
一方で論理の世界（特に数学）では「または」という言葉は「少なくとも一方が成り立つ」（両方成り立っても良い）という意味で使う。

日常での例を考えてみよう。
「今日の昼飯はカレーかうどんが食べたいな。」と言われたとき、「この人はカレーか、うどんのどちらか一つが食べたいのだな。」と思うのではなかろうか。
「この人はカレーもうどんも食べるのかな？」と思わない、ということがミソである。
もう一つ例を挙げると、「ご飯にする？それともお風呂にする？」と言われたとき、「どちらか一方を選んでほしいのだな」と思うのではなかろうか。
「こいつは俺が”飯を食いながら風呂に入る”なんて奇行をするとは想定してないであろう」と思うのではなかろうか。
ここにおける「〇〇か、△△」と「それとも」は排他的論理和の意味で用いられているわけである。

一方で、これを論理の世界で考えてみると「この人は、カレーかうどんのどちらか１つを食べる可能性もあるし、両方を食べる可能性もあるな」となるわけである。
つまり、これが注意を促した「または」の日常とは異なった使い方であり、「または」と「か」は似て非なるものである、ということである。

数学の命題の例を考えてみる。
$ab=0$は$a=0 \lor b=0$だが、この$\lor$は「いずれか一方が成り立つ」という意味ではなく、「$a=0$および$b=0$のうち、少なくとも一方が成り立つ。」という意味である。実際、$a=b=0$であったとしても$ab=0$である。

「かつ」、「または」について若干詳しく書くと、$p\land q$と$p \lor q$は数学的事実を主張しているというよりも、$p$と$q$が共にTであるとき$p\lor q$はTであるというように$\lor$を(同様に$\land$を)論理演算の真偽を決めている（ある種の言葉の約束事）のである。

言い回しについて

上述の通り、日常で使うときの「または」に対応する言い回しは様々ある。
例えば、「〇〇か、△△」やら「それとも」やら「もしくは」やら「あるいは」などがある。
これらは日常だけでなく論理の世界でも使われ、日常とは少々異なった使い方をする。

日常での例を挙げると、「黒もしくは紺インクの万年筆で記入してください。」と言われたときどう思うだろうか。
「黒、紺のどちらか一方の色のインクの万年筆で記入してほしいのだな」と捉えるのではないか。
すなわち、排他的論理和の意味で使われることが多い。

同様に「英語を学ぶべきか、あるいはウルドゥー語を学ぶべきか。」と言われたときどう思うだろうか。
「英語かウルドゥー語かどちらか一方を学びたいのだな」と思うのではなかろうか。
すなわち、排他的論理和の意味で使われる事が多い。

論理の世界でも「もしくは」やら「あるいは」は使われることがある。
筆者の経験からして、論理の世界においても「もしくは」やら「あるいは」は排他的論理和の意味で使われることがほとんどであるが、「両方成り立つ」という意味、すなわち論理の世界における「または」と同じ使い方をするものもある。

「言い回しについて」のまとめ

要は、日常で用いる「または」及びそれに準じた言い回しと、論理の世界で使う「または」は似て非なるものである。
さらには、「もしくは」やら「あるいは」には排他的論理和か、それとも論理の世界における「または」と同じ使い方なのかがはっきりしない場合があるため、多くの数学者は「もしくは」やら「あるいは」という言い回しを使わない事が多い。

もし仮に「もしくは」やら「あるいは」という言い回しが数学の文章で出てきた場合には、「排他的論理和なのか、それとも両方成り立つことがあるという意味で使っているのか」ということを注意しながら読まなければならない。

ちょっとした注意

以下、これらの論理演算（「かつ」やら「または」やら）を組み合わせた複雑な式が登場することもある。
通常の数に対する演算$\times$、$+$については、「カッコで指定してなければ、$\times$を先に計算する」という約束をするのだが、$\lor$および$\land$については特にそのような約束は無い。
そのため、どちらを先に計算するかを指定するため、カッコを多用することになる。
つまり、数では$p$と$q\times r$の和を$p+q\times r$と書くことができるが、論理の世界において$p$と$q\land r$の論理和は$p\lor (q\land r)$と書かねばならない（カッコを省略しない）。
これは後に記事化する集合に対しても同様である。

同値および論理演算の諸性質

　今更ながら、$\lnot$、$\land$、$\lor$、$\Rightarrow$を論理演算子といい、これらの操作をすることを論理演算という。

同値

　２つの命題$p$および$q$に対して、（その具体的な内容に関わらず、その真理値のみに注目して）$p$と$q$の真理値が一致するとき、その２つの命題は同値（equivalent）といい、$p\equiv q$で表す。

例えば、$p$：$1+1=2$、$q$：$\sin 1<1$としたとき、$p$も$q$もいずれも真であるから$p\equiv q$である。

この$\equiv$は論理の世界以外では、三角形の合同やら恒等式やら合同式やらにも用いられ、別の意味を持つ。

論理演算の諸性質

$p$を任意（すべての）の命題とするとき、すなわちどんな命題$p$に対しても、

$p$	$\lnot p$	$\lnot(\lnot p)$
T	F	T
F	T	F

$p$、$\lnot p$および$\lnot(\lnot p)$の真理値表

であるから、$\lnot (\lnot p)$（これについては単に$\lnot\lnot p$と書くこともある）と$p$は同値である。従って、$\lnot\lnot p\equiv p$が成り立つのである。同様にして、以下の諸性質を証明することが可能である。以下、$p$やら$q$やら$r$と書いたらば、任意の命題という意味を指す。

$\lnot\lnot p\equiv p$（反射律）（※証明済み）
任意の命題$p$について$p\land \lnot p$は常に偽である（無矛盾律）。また、任意の命題$p$に対して$p\lor (\lnot p)$は真である（排中律）。
$p \lor q \equiv q\lor p$, $p\land q\equiv q\land p$.　（交換律）
$p\lor (q \lor r) \equiv (p\lor q)\lor r$, $p\land (q \land r) \equiv (p\land q)\land r$　（結合律）
$p\lor (q \land p )\equiv (p\lor q)\land p\equiv p$　（吸収律）
$p\lor (q\land r)\equiv (p\lor q)\land (p\lor r)$, $p\land (q\lor r)\equiv (p\land q)\lor (p\land r)$　（分配率）
$p\lor p\equiv p$, $p\land p \equiv p$　（冪等律）
$\lnot (p\land q)\equiv (\lnot p)\lor (\lnot q)$, $\lnot(p\land q)\equiv (\lnot p)\lor (\lnot q)$　（ド・モルガンの法則（de Morganの法則）)

これらは全て真理値表を作ることで確かめられる。（量は多いが証明はシンプルなので一度手を動かしてみることを推奨する。）

これらはそれぞれ次のような意味である。

否定した命題を更に否定すると元の命題に戻る。
前回の記事（「命題の否定？」【論理と集合シリーズ】数学の文章を読むための論理的思考の基礎　その２）を参照。
「$p$または$q$」という命題と「$q$または$p$」という命題は一致し、「$p$かつ$q$」という命題と「$q$かつ$p$」という命題も一致する。
複数の「または」が存在する命題で、なおかつ「または」のみの命題であれば、どの「または」から考えても真理値は同じ。「かつ」についても同様。
「$p$または、(q\)かつ$p$」という命題も、「$p$または$q$、かつ$p$」という命題も$p$と同じ意味である。
数式の展開と同じような規則がある。
$p$または$p$も$p$かつ$p$も$p$と同じ意味である。
「$p$かつ$q$」という命題全体を否定すると、$p$と$q$をそれぞれ否定して、「かつ」が「または」に変わる。「$p$または$q$」についても同様。

ならば（含意）

　いよいよ本記事の主題に入っていく。命題に対する新たな論理演算として「ならば（含意）（$\Rightarrow$）」を導入する。

２つの命題$p$と$q$に対して、「$p$ならば$q$である（If $p$, then $q$）」という命題を「$p\Rightarrow q$」と表す。

「$p$ならば$q$である。」という命題を記述する際、「$p \rightarrow q$」と書く場合も無くはないのだが、これは推奨しない。
というのも、数学において$\rightarrow$は極限を表す記号としてよく用いられる記号だからである。
本シリーズにおいても「$p$ならば$q$である」という命題は一貫して「$p\Rightarrow q$」で表す。

「$p\Rightarrow q$」真理値を以下の真理値表で決める。

$p$	$q$	$p\Rightarrow q$
T	T	T
T	F	F
F	T	T
F	F	T

$p\Rightarrow q$の真理値表

これは「そういうルールなのだ」と理解してほしい。（※これについては後述）

数学におけるわかりやすい例を挙げよう。
「$1+1=2 \Rightarrow \sqrt{2}は無理数である。$」は真。
「$1+1=3 \Rightarrow \sqrt{2}は有理数である。$」も真。

真理値表の1,2行目については特に抵抗は無いであろう。
一方で3,4行目には抵抗があるかもしれない。
それはやはり日常的に用いる「ならば」とは直感的に異なる約束事だからである。
さらに言えば、日常的に用いる「ならば」は、「ならば」の前後に書いてあることに何か共通点がある。
特に前者が原因で後者がその結果、すなわち因果関係があると捉えるのが普通であろう。
例えば、息子が父親から

「次のテスト80点以上を取ったら、ゲームを買ってあげよう。」

と言われたとする。
$p$：テストで80点以上取る。
$q$：父がゲームを買い与える。
$r$：$p\Rightarrow q$
とする。

($p$,$q$,$p\Rightarrow q$)=(T,T,T)のとき
これは息子が80点を取り、父親はそれに報いた。このとき$r$は正しいだろう。
($p$,$q$,$p\Rightarrow q$)=(T,F,F)のとき
これもまた妥当。
息子が80点を取った、取らないに関わらず、父親はゲームを買わなかったという状況だ。
当然、息子は父親に不信感を持つであろう。
($p$,$q$,$p\Rightarrow q$)=(F,T,T)のとき
これは妥当か否かの判断が難しい。
息子が80点を取れなかったにもかかわらず、父がゲームを買い与えたのである。
「これは間違いだろ」と思えるのだが、実はそうでもない。
というのも父の慈悲により、息子の努力の過程を評価してゲームを買い与えたという場合もありえる。
そもそも父親が「$p$通りにならなかったのだから、結論$q$がどうであろうが知ったことではない。嘘はついていない。」といわれたらば、なるほど一理あるわけだ。
($p$,$q$,$p\Rightarrow q$)=(F,F,T)のとき
これは妥当であろう。
息子が悪い点を取り、父親はゲームを買い与えなかったという状況だ。

3.の場合に抵抗があるのではないかと思われる。
ここが日常で用いる「ならば」と論理の世界で用いる「ならば」の違いである。
日常で使う「ならば」と論理の世界で使う「ならば」はその真偽の規則が異なるため抵抗があるのである。
とはいえ、モヤモヤするであろう。
従って、「これはルールなんだ」と割り切ってほしいのである。
このモヤモヤこそ、日常と論理の世界との乖離を表しているのである。

筆者がこれを初めて学んだとき、「ってことはさ、今まで使ってた「ならば」の意味って間違ってたんだな」と思った。（実際は間違っていたのではなくてそもそも使い方が違ったということだが）

さて、これでようやく次の命題の真偽を判別できるようになった。

「クジラが爬虫類ならば日本国国会議事堂は２つ存在する。」

は真である。実際、クジラは爬虫類ではなく哺乳類であるため、「クジラは爬虫類である」という命題は偽である。
したがって、この命題は真である。
「「クジラが爬虫類ならば日本国国会議事堂は２つ存在する。」という命題はなぜ真なのですか？」という素朴な疑問に答えるなら拍子抜けかもしれないが「含意はそういう演算（約束事）だから」である。（モヤモヤは残る）

通常、命題$p\Rightarrow q$は$p$が真のときのことしか考えない（そのとき$q$が真になるか否か）気がするが、$p$が偽のときも定めておくのである。
実はこれにより、後の記事で紹介する「空集合は任意の集合の部分集合である。」という命題が成り立つのである。
結局の所、「直感に反しようがなんだろうが、そういう規則だ」の一言に尽きるのである。

再帰するが、なんとも言えないこの”モヤモヤ感”が日常と論理の世界との違いなのである。

ならば（含意）と同値な命題

　ここで一つ重要な事実を述べておく。それは「$p\Rightarrow q$と$(\lnot p)\lor q$の真理値」である。$(\lnot p)\lor q$の真理値表は以下である。

$p$	$q$	$(\lnot p)\lor q$
T	T	T
T	F	F
F	T	T
F	F	T

$(\lnot p)\lor q$の真理値表

これを見ると、$p \Rightarrow q$の真理値表と一致している。故に$p\Rightarrow q$とは$(\lnot p)\lor q$のことである、と決めることもある。
$p\Rightarrow q$の真偽を真理値表で決めようが、$(\lnot p)\lor q$で決めようが

定理１．$ p\Rightarrow q \equiv (\lnot p)\lor q $

である。

練習問題：真理値表を用いず、ド・モルガンの法則を用いることで「$\lnot(p\Rightarrow q)\equiv p\land (\lnot q)$」を示せ。
※解答は最後にあります。

命題に対する逆、裏、対偶

　命題$p\Rightarrow q$に対して、

$q \Rightarrow p$を$p\Rightarrow q$の逆（reverse）という。
$(\lnot p)\Rightarrow (\lnot q)$を$p\Rightarrow q$の裏という。（ほぼ使わない）
$(\lnot q)\Rightarrow (\lnot p)$を$p\Rightarrow q$の対偶（contraposition）という。

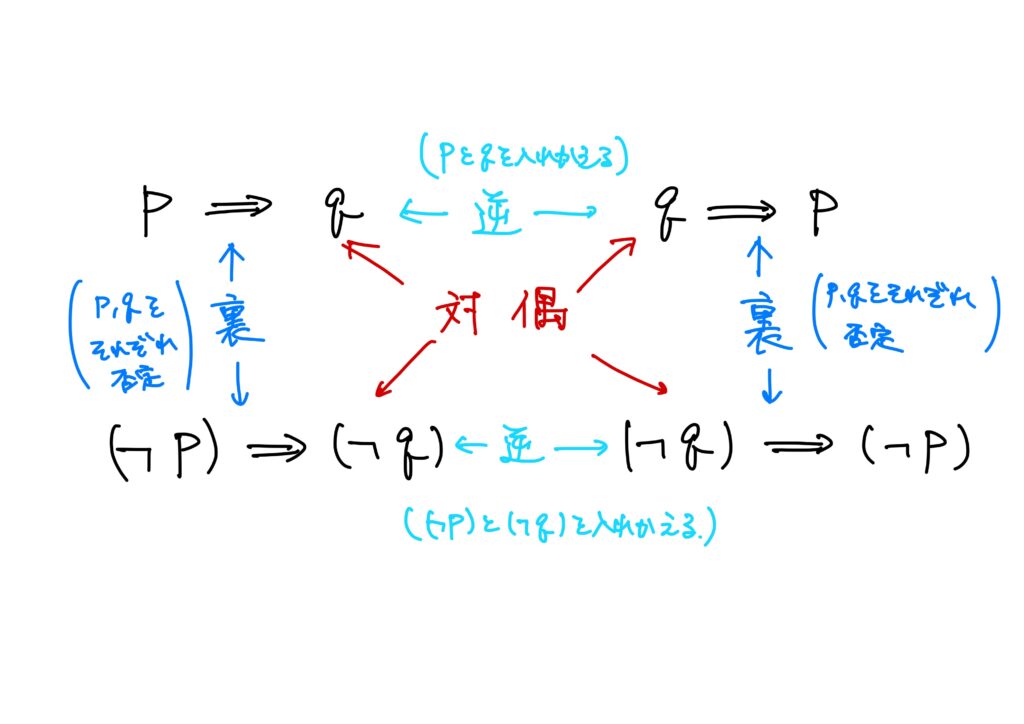
ここでも日常会話で用いる「逆」「裏」とは別であるということを述べておく。
日常的に「それって逆に言うと○○だよね？」やら「裏を返せばそれって〇〇だよね？」と使うことがあろう。
これらは「逆も裏も正しいよね？」というある種の思い込みから来ている。
というのも、論理の世界での逆および裏の真理値表を書いてみれば分かるのだが、$p\Rightarrow q$が真だったとしても、$q\Rightarrow p$は必ずしも真ではない。
実際、「円周率が有理数ならば$\sqrt{2}$は無理数である。」という命題は真であるが、その逆「$\sqrt{2}$は無理数であるならば円周率は有理数である。」は偽である。
さらに裏「円周率が有理数でないならば$\sqrt{2}$は無理数でない。」も偽である。

重要なのは「対偶」である。命題$p\Rightarrow q$の対偶$(\lnot q)\Rightarrow (\lnot p)$の真理値表は次である。

$p$	$q$	$(\lnot q)\Rightarrow (\lnot p)$
T	T	T
T	F	F
F	T	T
F	F	F

$(\lnot q)\Rightarrow (\lnot p)$の真理値表

これを見ると、$p\Rightarrow q$の真理値表と一致している。従って、

定理２．$(p\Rightarrow q) \Leftrightarrow ((\lnot q)\Rightarrow (\lnot p))$

である。

何故対偶が重要であるか、というと、ある命題を証明しようとしたとき、その命題の主張を直接的に証明することが難しい、または面倒な時がある。
例えば、次のような命題を考えてみる。

命題３．$n$を整数とする。このとき$n^2+1$が奇数であれば、$n$は偶数である。

これを直接的に証明しようとすると、次のようになる。

(証明) $n^2+1$が奇数であるので、$0$以上の整数$k$を用いて
$$n^2+1=2k+1$$
と書くことができる。
従って、$n^2=2k$であるから$n=\pm\sqrt{2k}$
と書ける。
ここで、$\pm\sqrt{2k}$($k\geq 0$)の形の整数が偶数であることを示せば、証明は完了である。
$N:=\pm\sqrt{2k}$ ($k\geq 0$)とおく。
$N\geq 0$のとき、$N$は整数であるから、$N$は偶数か奇数かのいずれか一方である。
$N$が奇数であれば、新たに整数$l\geq 0$を用いて$N=2l+1$と書ける。
従って、
\begin{eqnarray*}
N^2&=&(2l+1)^2 \\
&=&4l^2+4l+1 \\
&=&2(2l^2+2l)+1
\end{eqnarray*}
を得るのだが、$N=\sqrt{2k}$により$N^2=2k$であるため、$N^2$が偶数であることに矛盾する。
従って、$N\geq 0$のとき、$N=\sqrt{2k}$は偶数である。
$N<0$のときも同様である。（終）

というように証明はできるだが、証明が難しかったり、証明することが増えたりと面倒である。
この命題３．の対偶を考えてみる。

命題３．の対偶 $n$を整数とする。$n$が奇数ならば$n^2+1$は偶数である。

(証明) $n$が奇数であれば、新たな整数$m$を用いて$n=2m+1$と書ける。
従って、
\begin{eqnarray*}
n^2+1&=&(2m+1)^2+1 \\
&=&4m^2+4m+2 \\
&=&2(2m^2+2m+1)
\end{eqnarray*}
であるから$n^2+1$は偶数である。（終）

といった具合に、命題の内容も簡潔になり、証明の操作自体も楽になる。
特にこれといった基準はないのだが、どことなく「証明しにくいな」と思ったら対偶を考えてみるようにすると良い。

余談だが、筆者がこの逆、裏、対偶を学んだとき「これもやはり日常での使い方は間違ってたのだ」（実際は間違っていたのではなく、そもそも使い方が異なっていたということだが）と思った。
しかしながら「この規則は正しいな」と納得した記憶がある。

必要条件、十分条件、必要十分条件

　命題$p\Rightarrow q$が真であるとき、$p$は$q$の十分条件（$p$は$q$が成り立つための十分条件）、$q$は$p$の必要条件（$q$は$p$が成り立つための必要条件）という。
また、命題$p\Rightarrow q$と$q\Rightarrow p$が共に真であるとき、$p$は$q$の必要十分条件（$p$は$q$が成り立つための必要十分条件）と呼ぶ。
これを$p\Leftrightarrow q$で表す。
無論、これは$p$と$q$で対称であるため$p$と$q$を入れ替えても良い。
すなわち、$p$と$q$が同値とは、$p$が$q$の（または$q$が$p$の）必要十分条件であるときをいう、と言いかえることもできる。

余談

　本記事でも、さも当然かのように「$p$および$q$が命題であれば、$p\land q$, $p \lor q$, $\lnot p$, $p \Rightarrow q$, $p\Leftrightarrow q$もまた命題である」ことを認めている。
これを説明しようとするとちょっと骨が折れる。
とはいえ気になる方がいらっしゃるかもしれないので、少しだけ述べておく。

結論として先の主張は真である。というのも、「かつ（論理積）」、「または（論理和）」、「でない（否定）」、「ならば（含意）」および「同値」は論理演算子と呼ばれ、真理値集合$\{T,F\}$上で次のように決められた演算だからである。

※「演算」という言葉に馴染みがないかもしれないが、それは１個又は複数個の対象に対して決められた操作（ある種の計算といってもいい）を行うときのその操作（計算）の総称と思ってくれれば良い。

論理演算子	種別	使い方	意味
論理積($\land$)	二項演算	$p\land q$	$p$かつ$q$
論理和($\lor$)	二項演算	$p \lor q$	$p$または$q$
否定($\lnot$)	一項演算	$\lnot p$	$p$でない
含意(ならば)($\Rightarrow$)	二項演算	$p \Rightarrow q$	$p$ならば$q$
同値($\Leftrightarrow$)	二項演算	$p\Leftrightarrow q$	$p$と$q$は同値である。

代表的な論理演算子のまとめ

は、それぞれ

論理積($\land$)：$T \land T:= T$, $T\land F:= F$, $F\land T:=F$, $F\land F:=F$.
論理和($\lor$)：$T \lor T:=T$, $T \lor F:=T$, $F \lor T:=T$, $F \lor F:=F$.
否定($\lnot$)：$\lnot T:=F$, $\lnot F:=T$.
含意(ならば)($\Rightarrow$)：$T\Rightarrow T :=T$, $T\Rightarrow F :=F$, $F\Rightarrow T :=T$, $F\Rightarrow F :=T$.
同値($\Leftrightarrow$)：$T\Leftrightarrow T :=T$, $T\Leftrightarrow F :=F$, $F\Leftrightarrow T :=F$, $F\Leftrightarrow F :=T$.

で定められる。
ただし、「$A$:=$B$」は「$A$を$B$で定める」という意味である。
したがって、そもそも真偽を判定できる世界において決められた”演算”だから、$p$および$q$が命題であれば、$p$および$q$に対して「かつ」、「または」、「でない」、「ならば」、「同値」を含む主張もまた命題なのである。
ちなみに、次の主張は命題ではない。

「１億円が大金かつ１円がはした金ならば足が４本ある。」

$p$:１億円が大金である、$q$：１円がはした金である、$r$：足が４本ある、とすると$r$は命題だが、$p$および$q$は命題でないためである。

結

今回は「真理値表」、「かつ」、「または」、「ならば」について解説した。これらの真理値は全て真理値表により決めた。本記事で覚えてほしいことは３つ。それは「かつ」、「または」、「ならば」の真理値表である。これさえ覚えれば本記事の目標は達成されたも同然である。

ちなみに、「かつ」、「または」、「ならば」を導入することにより「命題とは？」【論理と集合シリーズ】数学の文章を読むための論理的思考の基礎　その１で挙げた命題の例である

「クジラが爬虫類ならば日本国国会議事堂は２つ存在する。」

という命題が真である事がわかる。
本文中にも書いたのだが、「なぜこの命題が真なのか？」と問われると、「論理はそういう規則だから」の一言に尽きるのである。
むしろ、「規則なのね、約束事なのね。」と割り切ってしまえば何ら難しいことはない。
しかも直感的に意味のわからない命題（「ならば」の前後に因果関係がない命題）にも真偽が判別できるようになる。
勿論全ての命題に真偽が判別できるようになるわけではないのだが。
特に「ならば」の部分でモヤモヤが起き、日常と論理の世界との違いが得られたことと思う。

次回は「述語論理」について解説する。特に「任意の」、「ある、存在する」について解説する。次回の記事まで読めば数学の文章を読む準備が整ったと言ってよいだろう。

乞うご期待！
質問、コメントなどお待ちしております！

（練習問題の解答）
$\lnot (p\Rightarrow q) \equiv \lnot((\lnot p)\lor q)\equiv (\lnot\lnot p)\land (\lnot q)\equiv p\land (\lnot q)$.

コメントをする

名前:名無しさん : 投稿日：2022/10/04(火) 11:02:40 ID：cwNTgxOTQ

分かりやすくためになります。
ド・モルガンの法則の論理記号での表現の部分に誤植がありました。
修正されますと他の読者の理解によりよいと思いご指摘致します。

返信
名前:名無しさん : 投稿日：2022/10/04(火) 11:15:32 ID：cwNTgxOTQ

(￢p)∨qの真理値表の最終行に誤植を発見しました。
読者の理解の便に修正されますとよろしいかと思います。

返信
名前:名無しさん : 投稿日：2022/10/04(火) 11:38:15 ID：cwNTgxOTQ

(￢q)⇒(￢p)の真理値表の最終行にも誤植を発見しました。
読者の理解の便に修正されますとよろしいかと思います。

返信

名前:オノコウスケ : 投稿日：2022/10/05(水) 03:52:31 ID：A3NjE2NjU

名無しさん

ご指摘ありがとうございます！
すべて修正致しました。

返信

名前:名無しさん : 投稿日：2023/05/07(日) 12:58:33 ID：IzMjAyOTI

必要条件、十分条件、必要十分条件のセクションの3行目,「これをp⇒qで表す。」ですが、
文脈からすると「p⇔q」でしょうか？

必要条件や十分条件の呼称が丸暗記だったのですが、この記事を読んだらすっきり理解できました。
必要条件、十分条件の定義には「p⇒qが真のとき」という前提があることを改めて認識しました。
このとき{p, q} = {F, F},{F, T}, {T, T} のいずれかなので
pが真になるにはまずqが真である必要があるので、qがpの必要条件、
pが真であればqが真であることを決定できるので、pがqの十分条件と呼ぶと理解しました。

50歳を過ぎて改めて数学を学びなおしておりますが、当ブログはとても参考になり大変感謝しております。

返信

名前:オノコウスケ : 投稿日：2023/05/07(日) 16:21:32 ID：c5MDAyNjY

名無し様

コメントありがとうございます。

>必要条件、十分条件、必要十分条件のセクションの3行目,「これをp⇒qで表す。」ですが、文脈からすると「p⇔q」でしょうか？
おっしゃるとおり、誤りでした。
訂正致しました。
ご指摘、ありがとうございました。

>必要条件や十分条件の呼称が丸暗記だったのですが、この記事を読んだらすっきり理解できました。必要条件、十分条件の定義には「p⇒qが真のとき」という前提があることを改めて認識しました。このとき{p, q} = {F, F},{F, T}, {T, T} のいずれかなのでpが真になるにはまずqが真である必要があるので、qがpの必要条件、pが真であればqが真であることを決定できるので、pがqの十分条件と呼ぶと理解しました。
そのご理解で結構だと思います。私は集合の包含関係をイメージしています。

>50歳を過ぎて改めて数学を学びなおしておりますが、当ブログはとても参考になり大変感謝しております。
こちらこそ、読んでいただき、誠に感謝しております。

返信

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

論理演算子	種別	使い方	意味
論理積(\(\land\))	二項演算	\(p\land q\)	\(p\)かつ\(q\)
論理和(\(\lor\))	二項演算	\(p \lor q\)	\(p\)または\(q\)
否定(\(\lnot\))	一項演算	\(\lnot p\)	\(p\)でない
含意(ならば)(\(\Rightarrow\))	二項演算	\(p \Rightarrow q\)	\(p\)ならば\(q\)
同値(\(\Leftrightarrow\))	二項演算	\(p\Leftrightarrow q\)	\(p\)と\(q\)は同値である。

\(p\)	\(q\)	\(p\land q\)
T	T	T
T	F	F
F	T	F
F	F	F

\(p\)	\(q\)	\(p\lor q\)
T	T	T
T	F	T
F	T	T
F	F	F

\(p\)	\(\lnot p\)	\(\lnot(\lnot p)\)
T	F	T
F	T	F

\(p\)	\(q\)	\(p\Rightarrow q\)
T	T	T
T	F	F
F	T	T
F	F	T