「数列が”発散する”って？」「”無限大”って？」【解析学の基礎シリーズ】

本記事の内容
序(小咄。無視してもいいです。)
数列の発散のイメージ
直感から論理へ
「$\infty$って数なの？」
1. 「どんな実数よりも大きいモノなんてあるんすか？」
数列の発散
例が発散することを証明してみよう！
結

本記事の内容

本記事は「数列の発散」について解説する記事である。
この記事を読むにあたり、数列の収束について知っているとより理解が進むと思われるので、以下の記事を参照してください。

序(小咄。無視してもいいです。)

※本来「小咄」は「気の利いた洒落やお色気を内容とした短い物語」らしいので、”小咄”と言ったらば洒落やお色気の話をしなければいけないが、悲しいことに筆者にはそんな文才はない…

実数の連続性を語る上で、「数列の収束」については説明したのだが、実は”発散”については何も言及していなかったことを思い出した。
数列の極限においては大きく分けて3つの状態がある。

収束
振動
発散

である。
以前に「収束」については厳密に話をしたのだが、「振動」および「発散」については一切言及していなかった。
この記事で「発散」について言及することで、

数列は収束、振動、発散のいずれかの状態が成り立っており、収束と発散を語ることで、”それ以外”という意味で間接的に振動について語ったことになる。

ということをしよう、というわけである。

また、発散を語ることで、「無限大」ということについての導入も済ます、という意図もある。

数列の発散のイメージ

以前数列の収束を説明する際に、サラッと説明したことが全てである。
数列$\{a_n\}_{n\in\mathbb{N}}$が発散する、ということの直感的な理解は、「値がどんどん際限なく大きくなっていく(または、小さくなっていく)」ということである。
言い換えれば、「ある値に近づくことなく、値が大きくなる(小さくなる)」ということである。

簡単ではあるが、例をいくつか挙げる。

例1.
$\{a_n\}_{n\in\mathbb{N}}$が$a_n=n$で定められているとする。このとき、数列$\{a_n\}_{n\in\mathbb{N}}$の値はある値に近づくことなく、際限なく大きくなる。
実際、

$a_1=1$,
$a_2=2$,
$a_3=3$,
$\dots$
$a_{100}=100$,
$\dots$
$a_{1000000}=1000000$,
$\dots$

となる。

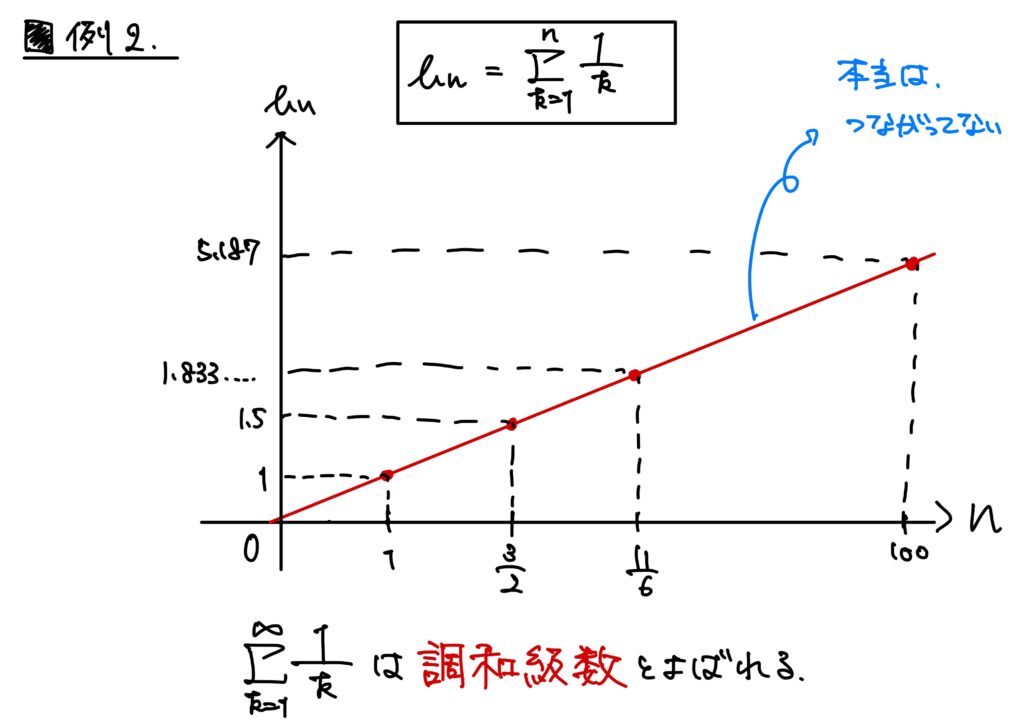
例2.
$\{b_n\}_{n\in\mathbb{N}}$が$\displaystyle b_n=\sum_{k=1}^{n}\frac{1}{k}$で定められているとする。
これも数列である。
この数列$\{b_n\}_{n\in\mathbb{N}}$の値もある値に近づくことなく、際限なく大きくなる。
実際、

$b_1=1$,
$b_2=\displaystyle\frac{3}{2}=1.5$,
$b_3=\displaystyle\frac{11}{6}=1.833333\dots$,
$\dots$
$b_{100}=\displaystyle\frac{14466636279520351160221518043104131447711}{2788815009188499086581352357412492142272}=5.187$,
$\dots$

である。

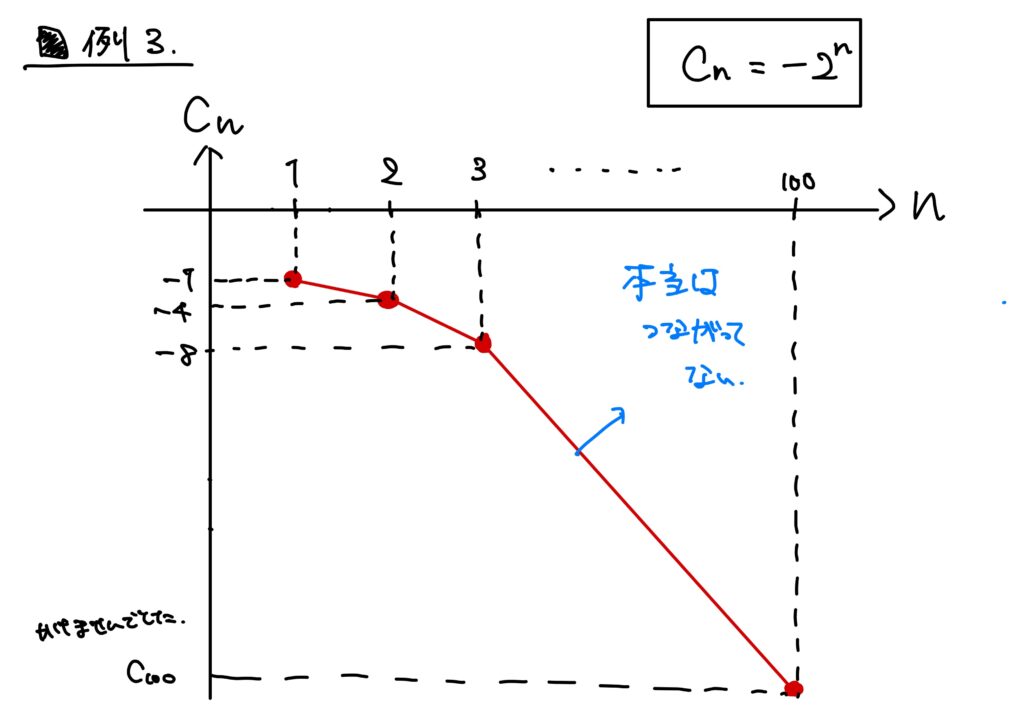
例3.
$\{c_n\}_{n\in\mathbb{N}}$が$\displaystyle c_n=-2^n$で定められているとする。この数列$\{c_n\}_{n\in\mathbb{N}}$の値はある値に近づくことなく、際限なく小さくなる。

$c_1=-2$,
$c_2=-4$,
$c_3=-8$,
$\dots$
$c_{100}=-1267650600228229401496703205376$,
$\dots$

直感から論理へ

数列の収束を説明する際、”限りなく近づく”という直感を論理で記述するために「数学的に”近い”ってどういうこと？」を説明した(「数列の収束って？」)。

実は、そのとき”限りなく大きくなる(小さくなる)”ということについてもほんのちょっとだけ説明したのだが、ズルをしてあまり語らなかった。
(「何となく分かるっしょ？」ということでちょろまかしてしまった。ごめんなさい。)

さて、”大きくなる”および”小さくなる”というのは、”大きい”および”小さい”という言葉から来ているわけだが、大きい、小さい、すなわち大小関係というのは、比較する対象があって初めて分かることである。
【論理と集合シリーズ】その１で述べたように、「１億円は大金である。」という主張は命題でない。
しかし、一方で基準を定めることで命題となるのだった。
つまり、２つのモノを比較することによって初めて大小関係は意味を持つのである。
従って、”大きくなる”ということは、とある比較対象があって、それを大きい方へどんどん更新していっても大小関係は変わらないということである。
“限りなく”ということは、いくら大きい方へ比較対象を更新したとしても、という意味である。
“小さくなる”も同様である。

これを少々言い換えてみると、「どんな実数に対しても、その実数よりも大きい。」ということが”限りなく大きい”ということなのである。
同様に、「どんな実数に対しても、その実数よりも小さい。」ということが”限りなく小さい”ということなのである。

これを論理式で書けば、

$A$は限りなく大きい。
$$(\forall U\in \mathbb{R})\ A>U$$
$B$は限りなく小さい。
$$(\forall L\in\mathbb{R})\ B<L$$

実は、この$A$および$B$がそれぞれ$\infty$および$-\infty$なのである。

「$\infty$って数なの？」

結論から言おう。
数ではない。
しかし、「どんな実数よりも大きいモノ」を表す記号で数のように扱うことができる。

「ん？」と思うかもしれないが、$\infty$が数であるか否かは置いておいても、少なくとも実数ではないことが分かる。
仮に$\infty$が実数であったとする。
すなわち、$\infty\in\mathbb{R}$であったとする。
このとき、$(\forall U\in\mathbb{R})\ \infty>U$であり、かつ$\infty\in\mathbb{R}$なのだから、$\infty>\infty$が成り立つ。
しかしながら、任意の$a,b\in\mathbb{R}$に対して、$a=b$または$a>b$または$a\infty$が同時に成り立ってしまっている。
故に矛盾である。

別の言い方をしてみよう。
仮に$\infty\in\mathbb{R}$であったとする。
まず、任意の$a\in\mathbb{R}$に対して、$a<a+1$が成り立っており、$a+1\in\mathbb{R}$である。
従って、$x=\infty+1\in\mathbb{R}$であり、かつ$\infty<\infty+1=x$でなければならない。
しかしながら、これは、$x<\infty$かつ$\infty<x$が同時に成り立っている、ということになり矛盾である。
同様にして、$-\infty$も実数でない。

実は、$\displaystyle\frac{1}{\infty}$やら高校数学で出現した$\infty$に関わるモノは全て実数でない。

「どんな実数よりも大きいモノなんてあるんすか？」

答えは、「”モノ”があるかは(筆者は)わからないが(ごめんなさい)、少なくとも数はある。」である。
これを保証しているのが、実数の連続性を語る際に散々出現したアルキメデスの原理(「区間縮小法とアルキメデスの原理からデデキントの定理を証明しよう！」)なのである。

これをもう一度明示しておくと、

アルキメデスの原理 $$(\forall a\in\mathbb{R}_{>0})(\forall b\in\mathbb{R}_{>0})(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ b<N_0a$$ ただし、$\mathbb{R}_{>0}=\{x\in\mathbb{R}\mid x>0\}$である。

これは任意の正の実数$a,b$で成り立つのだから、$a=1$としても成り立つ。
従って、任意の正の実数$a$に対して、それよりも大きい自然数$N_0$が存在する、と言っているわけである。
したがって、どんな正の実数よりも大きい自然数が存在する、ということなのである。

こう考えると、Arichimedesさんってすげえな、と思う。

「あれ？じゃあ実数の集合って上に有界なんじゃね？」

「あら？任意の正の実数が上から抑えられてる(任意の正の実数より大きい自然数がある)のだから、実数の集合って上に有界なんじゃね？」と思うかもしれない。
しかし、そんなことはない。
有界でない(非有界と言ったりもする)。

理由は単純で「自然数だって実数じゃん。」ということである。
アルキメデスの原理から任意の正の実数$a$に対してそれよりも大きい$n\in\mathbb{N}\subset\mathbb{R}$がある。
ということは、$n\in\mathbb{R}$なのだから、再度アルキメデスの原理により$n$よりも大きい$N\in\mathbb{N}\subset\mathbb{R}$が存在する。
というようにこの操作は何回でもできる。
従って、ある特定の実数があって、どんな実数もその特定の実数よりも小さい、ということは起こらない。
故に実数の集合は上に有界ではない。

数列の発散

ようやっと本題といったところ。
つまり、数列の値が”限りなく大きくなる(小さくなる)”ということを論理式であらわそう、というわけである。
とはいえ、本質的にはすでに述べたように、どんな実数よりも大きい(小さい)ということが発散なのである。

ちなみに、数列の収束について少々復習をしておこう。
数列$\{a_n\}_{n\in\mathbb{N}}$が$a$に収束する、というのは、どんな正の実数$\epsilon$を取ってきたとしても、それに対応するある番号$N$が存在して、$N$以上の自然数$n$($N$以降の番号$n$に対して、$|a_n-a|<\epsilon$を満たすこと。

だった。
要は、「ある番号以降の$\{a_n\}_{n\in\mathbb{N}}$の値は$a$と十分近い。」ということだった。数列の発散についても似たようなもので、「ある番号以降の$\{a_n\}_{n\in\mathbb{N}}$の値はどんな実数よりも大きい」ということである。

では、明示しよう。

数列の発散
$\{a_n\}_{n\in\mathbb{N}}$が数列であるとする。

$\infty$への発散
$-\infty$への発散

例が発散することを証明してみよう！

数列が発散するというのはどういうことかは分かった。
では、実際に証明をしてみよう！

例1.について

例1. $\displaystyle \lim_{n\to\infty}n=\infty$

この命題の証明は難しくないので是非挑戦してみてほしい！

(証明)
示したいことは、$a_n=n$としたとき、
$$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow a_n>U)$$
が成り立つことである。
すなわち、任意の実数$U$に対して、上記を満たすような番号$N$を見つけてくれば良い。
アルキメデスの原理から、
$$(\forall a\in\mathbb{R}_{>0})(\forall b\in\mathbb{R}{>0})(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ b|U|+1>U$$
が成り立つ。
従って、
$$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow a_n>U)$$
が成り立ったので、$\displaystyle \lim_{n\to\infty}n=\infty$である。
(Q.E.D.)

この証明も「もし、こんな$N$があったらいいなあ」という期待からアルキメデスの原理に至る。

例2.について

例2. $\displaystyle \lim_{n\to\infty}\sum_{k=1}^{n}\frac{1}{k}=\infty$

この数列は調和級数と呼ばれる有名な数列である。
この命題の証明は少々特殊なので、流れを説明する。

(ステップ1) $\displaystyle \sum_{k=1}^{n}\frac{1}{k}$よりも小さい数列を取ってくる。
(ステップ2) とってきた数列が発散することを示す。
(ステップ3) 追い出しの原理を用いて$\displaystyle \sum_{k=1}^{n}\frac{1}{k}$が発散することを示す。

(証明)

(ステップ1)
任意の自然数$n$に対して、$n\geq 2^m$を満たす$m\in\mathbb{N}\cup\{0\}$が存在する。
実際、自然数$n$を素因数分解すると、$n=2^i(2j+1)$($i,j\in\mathbb{N}\cup\{0\}$)と書くことができる。(素因数分解して、偶数の部分と奇数の部分に分けた、ということ。)
すなわち、上記を満たすような$i,j\in\mathbb{N}\cup\{0\}$が存在する。
ここで、$2^i(2j+1)\geq2^i$であるから、$m$として$i$を採用すれば、任意の自然数$n$に対して、$n\geq2^m$という$m\in\mathbb{N}\cup\{0\}$が存在する。

従って、$\displaystyle \sum_{k=1}^{n}\frac{1}{k}>\sum_{k=1}^{2^m}\frac{1}{k}$が成り立つ。
ここで、1つ補題を与える。

補題4. $\displaystyle \sum_{k=1}^{2^m}\frac{1}{k}\geq 1+\frac{m}{2}$

(補題4.の証明)

数学的帰納法で証明する。

$m=1$のとき
$\displaystyle \sum_{k=1}^{2^1}=1+\frac{1}{2}=\frac{3}{2}$であり、$1+\displaystyle\frac{m}{2}=\frac{3}{2}$であるから成り立つ。
$m=t$のとき成り立つとする。
このとき、
$$\sum_{k=1}^{2^t}\frac{1}{k}\geq 1+\frac{t}{2}$$
が成り立つ。
$m=t+1$のとき、
$$\sum_{k=1}^{2^{t+1}}\frac{1}{k}\geq 1+\frac{t+1}{2}$$
が成り立てば良い。
\begin{eqnarray}
\sum_{k=1}^{2^{t+1}}\frac{1}{k}&=&\sum_{k=1}^{2^t}\frac{1}{k}+\sum_{k=2^{t}+1}^{2^{t+1}}\frac{1}{k} \\
&\geq& 1+\frac{t}{2}+\sum_{k=2^{t}+1}^{2^{t+1}}\frac{1}{k}
\end{eqnarray}
従って、$t\geq 1$で
$$\sum_{k=2^{t}+1}^{2^{t+1}}\frac{1}{k}\geq \frac{1}{2}$$
が成り立てば良いことになる。
\begin{eqnarray}
\sum_{k=2^{t}+1}^{2^{t+1}}\frac{1}{k}&=&\frac{1}{2^t+1}+\frac{1}{2^t+2}+\dots +\frac{1}{2^{t+1}} \\
&=&\frac{1}{2^t+1}+\frac{1}{2^t+2}+\dots +\frac{1}{2^t+2^t} \\
\end{eqnarray}
ここで、任意の$a\in\mathbb{N}$に対して、$2^a>a$が成り立つ(「区間縮小法とアルキメデスの原理からデデキントの定理を証明しよう！」)ので、
\begin{eqnarray}
\frac{1}{2^t+1}+\frac{1}{2^t+2}+\dots +\frac{1}{2^t+2^t}&>&\frac{1}{2^t+2^t}+\frac{1}{2^t+2^t}+\dots +\frac{1}{2^t+2^t} \\
&=&\frac{1}{2^t+2^t}\cdot 2^t=\frac{1}{2}
\end{eqnarray}
従って、$t\geq 1$で
$$\sum_{k=2^{t}+1}^{2^{t+1}}\frac{1}{k}\geq \frac{1}{2}$$
が成り立つので、
$$\sum_{k=1}^{2^{t+1}}\frac{1}{k}\geq 1+\frac{t+1}{2}$$
が成り立つ。
(Q.E.D.)

(ステップ2)
今、$\displaystyle b_m=1+\frac{m}{2}$で定められる新たな数列$\{b_m\}_{m\in\mathbb{N}}$が得られた。
ステップ2としてこの数列が$\infty$に発散することを示す。

補題5. $\displaystyle \lim_{m\to\infty}\left(1+\frac{m}{2}\right)=\infty$

これは殆ど例1.の証明と同じであるので、ぜひ証明に挑戦してもらいたい。

(補題5.の証明)
示したいことは、
$$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ \left(\forall n\in\mathbb{N}\ m\geq N\Rightarrow 1+\frac{m}{2}>U\right)$$
である。
すなわち、任意の実数$U$に対して、上記を満たすような番号$N$を見つけてくれば良い。
アルキメデスの原理から、
$$(\forall a\in\mathbb{R}_{>0})(\forall b\in\mathbb{R}{>0})(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ b<N_0a$$
が成り立つ。
従って、$a=1,\ b=2(|U|+1)$としても成り立つ。
故に$\displaystyle |U|+1<\frac{N_0}{2}$という$N_0$を見つけてくることができる。 $N$として$N_0$を採用すると、任意の$m\geq N$なる自然数$m$に対して、
$$b_m=1+\frac{m}{2}>\frac{m}{2}\geq\frac{N}{2}>|U|+1>U$$
が成り立つ。
従って、
$$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall m\in\mathbb{N}\ m\geq N\Rightarrow b_m>U)$$
が成り立ったので、$\displaystyle \lim_{n\to\infty}\left(1+\frac{m}{2}\right)=\infty$である。
(Q.E.D.)

(ステップ3)
次に追い出しの原理を述べる。
一言で言えば、発散する数列よりも大きい値を取る数列も発散する、ということである。

補題6.(追い出しの原理) 実数列$\{a_n\}_{n\in\mathbb{N}}$および$\{b_n\}_{b\in\mathbb{N}}$に対して、 $$(n\geq 1)\ a_n\leq b_nかつ\lim_{n\to\infty}a_n=\infty$$ が成り立っているとする。このとき、$\displaystyle \lim_{n\to\infty}b_n=\infty$である。

(補題6.の証明)
$\displaystyle \lim_{n\to\infty}a_n=\infty$であるので、
$$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow a_n>U)$$
が成り立っている。
今、$a_n\leq b_n$であるのだから、
$$b_n\geq a_n>U$$
が成り立つ。
すなわち、
$$(\forall U\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow b_n>U)$$
が成り立っているので、$\displaystyle \lim_{n\to\infty}b_n=\infty$である。
(Q.E.D.)

では(ステップ3)の証明に戻る。
今までのことをまとめれば、
$$\sum_{k=1}^{n}\frac{1}{k}>\sum_{k=1}^{2^m}\frac{1}{k}>1+\frac{m}{2}$$
であり、かつ
$$\lim_{m\to\infty}\left(1+\frac{m}{2}\right)=\infty$$
である。
従って、追い出しの原理から、
$$\lim_{m\to\infty}\sum_{k=1}^{2^m}\frac{1}{k}=\infty$$
が成り立つ。
さらに、$n\geq2^m$なのだから、$m$が限りなく大きくなるとき(つまり、$m\to\infty$のとき)、$n\to\infty$である。
従って、再度追い出しの原理により、
$$\lim_{n\to\infty}\sum_{k=1}^{n}\frac{1}{k}=\infty$$
である。
(Q.E.D.)

例3.について

例3. $\displaystyle \lim_{n\to\infty}(-2^n)=-\infty$

この証明も至って難しいわけではない。
例1.の証明が理解できていれば何ら問題ではない。
故に、この証明もぜひ挑戦してみてほしい。

(証明)
示したいことは、
$$(\forall L\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow -2^n<L)$$
である。
すなわち、任意の実数$L$に対して、上記を満たすような番号$N$を見つけてくれば良い。
アルキメデスの原理から、
$$(\forall a\in\mathbb{R}_{>0})(\forall b\in\mathbb{R}_{>0})(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ b<N_0a$$
が成り立つ。
従って、$a=1,\ b=|L|+1$としても成り立つ。
故に$-|L|-1<-N_0$という$N_0$を見つけてくることができる。さらに、任意の自然数に対して、$2^n>n$が成り立つ(「区間縮小法とアルキメデスの原理からデデキントの定理を証明しよう！」を参照)。
以上のことを踏まえて、$N$として$N_0$を採用すると、任意の$n\geq N$なる自然数$n$に対して、
$$-2^n<-n\leq -N<-|L|-1<L$$
が成り立つ。
従って、
$$(\forall L\in\mathbb{R})(\exists N\in\mathbb{N})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ n\geq N\Rightarrow -2^n<L)$$
が成り立ったので、$\displaystyle \lim_{n\to\infty}(-2^n)=-\infty$である。
(Q.E.D.)

結

今回は少々予定を変えて、数列の発散について解説した。
また、「無限大」についての初歩も述べた。

数列が$\infty$に発散する、というのは、数列のある番号以降の値がどんな実数よりも大きい状態を指す。
同様に数列が$-\infty$に発散する、というのは、数列のある番号以降の値がどんな実数よりも小さい状態を指す。

また、無限大はどんな実数よりも大きい”モノ”であって、実数でない。
あくまで記号なのである。

次回こそ関数の極限の話をする。
本来は関数の極限の前に無限大の話はしなくても良かった気もするのだが、いずれ必要になるであろう、ということで、思い至ったため書いた。

乞うご期待！質問、コメントなどお待ちしております！

この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください！
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ１冊持っておくと良いと思います！

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34